1. 각도법(60분법)

60분법은 직각을 90등분 한 방법이다. 삼각형을 쉽게 다루기 위해서 만들어졌다.

우리가 어릴 때 부터, 혹은 일상에서도 가장 흔히 접하는 각도 측정 방법은 60분법이다. 60분법은 직각을 90등분 한 방법이다. 굳이 이 각도법이 60분법으로 불리는 것은 이 각도법이 60진법을 따라 도, 분 초로 하위 단위를 부르기 때문이라고 생각한다. 즉, 1/60도를 1 분으로 부르고, 1/60분을 1초라고 부른다.

그런데, 왜 직각을 90등분 한 것을 1도라고 정의했을까? 여러가지 설이 있지만, 필자는 이것이 삼각형을 쉽게 다루기 위해서 고안된 아이디어라고 생각한다. 10진법 수 체계를 사용하는 문화에서는 ‘기준’이되는 숫자로 10, 100, 1000 등을 사용하는 것이 유용하다. 물이 끓는 온도를 100도로 정의한 것 처럼 말이다. 그런 의미에서 직각을 100도로 정의하는 것은 매우 합리적인 선택일 수 있다. 실제로 직각을 100등분한 gradian이라는 각도 체계가 있다¹.

10진법 문화권에 살고있는 우리에게 gradian 시스템은 직관적임에도 불구하고 도형을 분석할 때 어려움이 생길 수 있다. 가령, 정삼각형을 생각해보자. 흔히 알고 있듯이 흔히 사용하는 60분법에서 정삼각형의 한 각의 크기는 60도이다. 여기에 gradian 시스템을 적용하면 어떨까? 66.67도가 된다. 다각형을 이해하기 위해서는 삼각형을 잘 이해하는 것이 중요하다. 그렇기 때문에, 즉, 평면 도형의 분석을 용이하게 만들기 위해 66.67도가 아닌 가장 근접한 숫자이면서도 약수가 많은 60도로 삼각형의 한 각을 정의한 것이 아닐까? 그렇기 때문에 우리가 흔히 사용하는 60분법을 수학에서 차용한 것은 아닐까하고 생각한다.

2. 호도법

호도법과 각도법은 각도를 이해하는 관찰 시점의 차이이며, 호도법은 원의 기하학적 특성을 잘 활용했다.

호도법은 영어로는 radian이라고 하는데, 이 의미는 원의 반지름을 의미하는 radius에서 온 것이라고 생각한다. 호도법이라는 한자용어는 호의 길이를 이용하여 각도(angle)를 재는 방법을 의미한다고 생각한다. 두 단어 모두 호도법의 특성을 잘 담은 단어라고 생각한다.

가끔 외국어 단어의 한자어 또는 한국어로 번역된 결과를 보게 되면, 답답하고 안타까운 경우도 종종 있지만, 어떤 경우는 번역된 단어가 원래 단어의 의미를 뛰어넘는 굉장한 번역들이 보여 감탄하게 된다. 나는 호도법(弧度法)이 그런 경우에 해당한다고 생각한다. 호도법의 진정한 의미를 알게 된다면 나의 의견에 동의하게 될 것이다.

각도법(degree)과 호도법(radian)의 차이는 원이 작도 될 때의 관찰 시점에 있다. 원이 작도되는 과정을 떠올려보자. 각도법은 원의 중심에서 원이 작도되는 과정을 보면서 ‘내 고개가 얼마나 올라갔나’를 수치화 시킨 것이고, 호도법은 원을 작도하는 연필의 입장에서 ‘(반지름 대비) 연필이 긁고간 길이가 얼마인가?’를 보는 것이다. 이 때 연필이 긁고 간 길이를 ‘호(弧)’라고 하는데 말 그대로 호도법은 호의 길이를 이용해 만든 각도(angle) 시스템인 것이다.

일반적으로 1 radian은 다음과 같이 정의하게 된다.

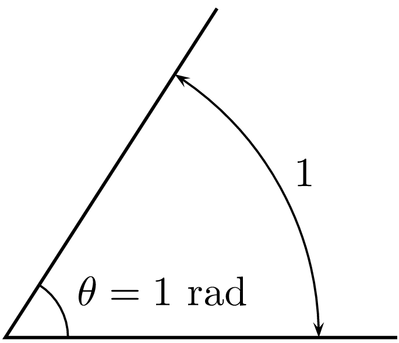
1 라디안(radian)은 원둘레 위에서 반지름의 길이와 같은 길이를 갖는 호에 대응하는 중심각의 크기로 무차원의 단위이다. 보다 일반적으로 라디안 값은 원에서의 호와 반지름의 길이의 비율과 같다. 즉, θ = s /r 이다, 여기서 θ 는 라디안으로 주어진 각도, s 는 호의 길이, r 은 반경이다. (출처 : Wikipedia)

호도법이 더 논리적이고 수학적인 이유는 원이 가지는 수학적인 특성을 잘 활용했기 때문이다. 원은 (반)지름과 둘레가 항상 일정한 비율을 가지고 있다. 즉, 어떤 원이더라도 반지름과 원의 둘레는 항상 $2\pi$만큼의 비율을 가지고 있게 되고, radian 각도(angle) 시스템은 원의 특성을 잘 반영한 시스템이라고 할 수 있다.

3. 각도법 대신 호도법을 쓰는 이유?

각도법 대신 호도법을 쓰는 가장 중요한 이유는 삼각함수 미분에 있다. 쉽게 말해서, 삼각함수를 미분할 때 결과가 깔끔하게 나오게 하기 위해서이다. 이 내용을 확인하기 위해 사인함수의 미분을 생각해보자.

\[\frac{d}{dx}\sin(x) = \lim_{h\rightarrow 0}\frac{\sin(x+h)-\sin(x)}{h}\] \[\Rightarrow \lim_{h\rightarrow 0}\frac{\sin(x)\cos(h)+\cos(x)\sin(h)-\sin(x)}{h}\]

여기서, $\lim_{h\rightarrow 0}\cos(h)=1$이므로,

\[\Rightarrow \lim_{h\rightarrow 0}\frac{\sin(x)-\sin(x)+\cos(x)\sin(h)}{h}=\lim_{h\rightarrow 0}\frac{\cos(x)\sin(h)}{h}\] \[=\cos(x)\lim_{h\rightarrow 0}\frac{\sin(h)}{h}\]

여기서, $\lim_{h\to 0}{\sin(h) \over h}$의 값에 대해 알아보자 (조임정리).

아래 그림에서 파란색, 초록색, 노란색으로 표시한 영역의 넓이를 생각해보면, 항상 그 넓이는 파란색, 초록색, 노란색 순서대로 크다. 굳이 수식으로 표현하자면 다음과 같다. 여기서 초록색은 길이가 1이고 각도가 $\theta$인 호의 넓이이다.

넓이(파란색)$\leq$ 넓이(초록색) $\leq$ 넓이(노란색)

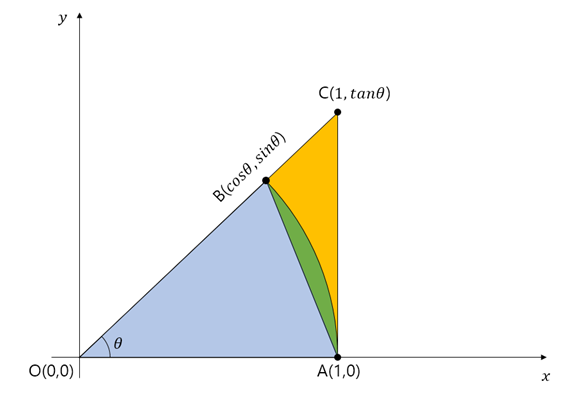
이제, 넓이(파란색), 넓이(초록색), 넓이(노란색)를 수학적으로 서술하되, 각도법을 이용한 경우와 호도법을 이용한 경우를 따로 따로 알아보자.

➀ 각도법을 이용하는 경우

넓이(파란색)$\leq$ 넓이(초록색) $\leq$ 넓이(노란색)의 관계는 다음과 같이 쓸 수 있다.

\[\frac{1}{2}\times 1 \times \sin(\theta °) \leq \pi \times 1^2 \times \frac{\theta °}{360 °}\leq \frac{1}{2}\times 1 \times \tan(\theta °)\]

다시 쓰자면,

\[\frac{\sin(\theta °)}{2}\leq \pi \frac{\theta °}{360 °}\leq \frac{\tan(\theta °)}{2}\]

양변에 360도를 곱하고, $\pi$로 나눠주면,

\[\frac{360 °}{\pi}\times \frac{\sin(\theta °)}{2}\leq \theta °\leq \frac{360 °}{\pi}\times\frac{\tan(\theta °)}{2}\]

양변을 $\sin(\theta °)$로 나눠주고 식을 정리하면,

\[\frac{180 °}{\pi}\leq\frac{\theta °}{\sin(\theta °)}\leq\frac{180 °}{\pi}\times\frac{1}{\cos(\theta °)}\]

분자 분모를 뒤집어주면,

\[\frac{\pi}{180 °}\geq \frac{\sin(\theta °)}{\theta}\geq\frac{\pi}{180 °}\times \cos(\theta °)\]

따라서 $\theta ° \to 0$으로 수렴할 때,

\[\frac{\sin(\theta °)}{\theta °}\]

는

\[\frac{\pi}{180 °}\]

로 수렴한다.

➁ 호도법을 이용하는 경우

마찬가지 방법으로 넓이(파란색) $\leq$ 넓이(초록색) $\leq$ 넓이(노란색)의 관계를 호도법을 이용해 쓸 수 있다.

\[\frac{1}{2}\sin(\theta)\leq \pi \frac{\theta}{2\pi}\leq \frac{1}{2}\tan(\theta)\]

다시 쓰자면,

\[\frac{\sin(\theta)}{2}\leq \frac{\theta}{2}\leq \frac{\tan(\theta)}{2}\]

전체적으로 2를 곱해주고, $\sin (\theta)$로 나눠주면,

\[1\leq \frac{\theta}{\sin(\theta)}\leq \frac{1}{\cos(\theta)}\]

분자, 분모를 뒤집어주면,

\[1\geq \frac{\sin(\theta)}{\theta} \geq \cos(\theta)\]

따라서, $\theta \to 0$으로 수렴할 때, $\frac{\sin\theta}{\theta}$는 1로 수렴한다.

다시, 삼각함수의 미분으로.

다시 식 (4)를 각도법과 호도법으로 각각 나타내면,

➀ 각도법을 이용하면,

\[\frac{d}{dx}\sin(x)=\cos(x)\lim_{h\rightarrow 0}\frac{\sin(h)}{h}\] \[=\cos(x)\times \frac{\pi}{180°}\]

➁ 호도법을 이용하면,

\[\frac{d}{dx}\sin(x) = \cos(x) \lim_{h\rightarrow 0}\frac{\sin(h)}{h}\] \[=\cos(x)\]

따라서, 호도법을 이용하면 삼각함수 미분을 더 깔끔하게 수행할 수 있는 장점이 있다.