Prerequisites
해당 포스트에 대해 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
푸리에 변환이란?
푸리에 변환은 신호의 주파수 분석을 수행할 때 이용된다.
조금 쉽게 예를 들면 톤이 매우 낮은 남자와 톤이 높은 여자가 동시에 말을 한다고 생각해보자.
이 때 우리가 듣게 되는 소리는 낮은 음과 높은 음이 섞인 신호 일 것이다.
여기서 우리가 알고싶은 정보는 다음과 같다.
- 낮은 음과 높은 음의 주파수 값은 어떻게 될까? (즉, 얼마나 높고 낮은지를 수치화 하고싶다는 의미)
- 낮은 음과 높은 음의 신호 크기 비율은 어떻게 될까? (한마디로, 둘의 목소리가 얼마나 컸나)
푸리에 변환의 사용 예시
위의 예시를 조금 더 구체적이 신호와 그에 대한 푸리에 변환 분석으로 확인해보자.
아래의 그림 1에는 50Hz의 sine파와 120Hz의 사인파가 합쳐진 신호가 도시되어 있다.
즉, 낮은 주파수의 신호 하나와 높은 주파수의 신호가 합쳐져 있는데, 낮은 주파수와 높은 주파수의 신호는 0.7, 1 의 진폭을 갖도록 설정하였다.
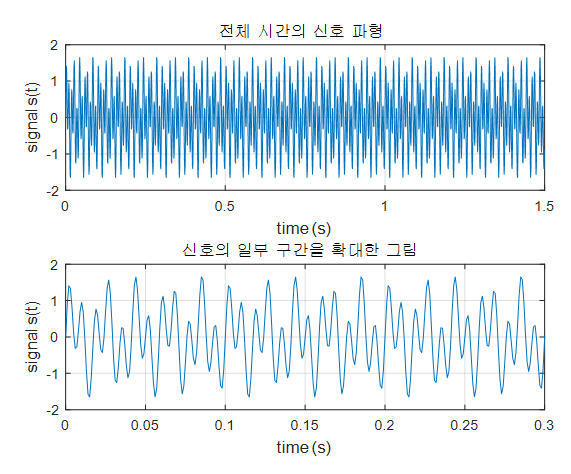
그림 1. 50Hz 및 120 Hz의 정현파가 섞여있는 신호
만약 우리가 어떤 배경 정보 없이 그림 1과 같은 신호를 받았다고 했을 때 이 전체 신호의 성분을 알 수 있을까?
다시 말해, 낮은 음과 높은 음의 주파수 값과 그 신호 크기 비율을 알 수 있을까?
우리는 푸리에 변환을 적용하면 아래의 결과와 같이 신호의 성분을 얻어낼 수 있다는 사실을 알 수 있다.
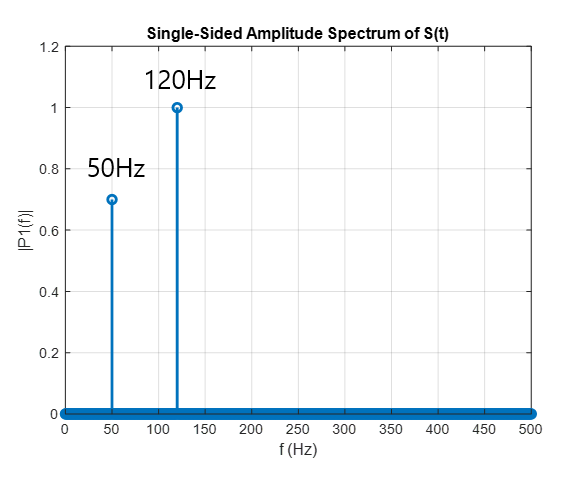
그림 2. 푸리에 변환 결과 50Hz, 120Hz의 두 주파수 성분이 포함되어 있는 신호임을 역으로 추정할 수 있다.
신호 역시도 벡터로 볼 수 있다.
그럼 지금까지 우리가 공부했던 선형대수학과 푸리에 변환은 어떤 관계가 있을까?
우선 가장 중요한 개념은 ‘신호도 벡터로 볼 수 있다’는 점이다.
이게 무슨 말일까?
벡터의 기본 연산 편에서는 ‘벡터란 숫자를 순서대로 나열한 것’이라는 관점을 소개한 바 있다.
앞서 예시에서 소개한 음성 신호는 녹음기를 통해서 얻은 소리의 압력을 숫자로 변환해 순서대로 나열한 것에 불과하다는 사실을 다시 생각해보자.
가령, 녹음기를 통해 우리의 음성 신호를 녹음한다고 했을 때, 소리 파형에서 1초 당 1개의 데이터를 취득해올 수 있는 성능을 가진 녹음기라고 하면,
총 10초 녹음했을 때 얻게 되는 데이터는 10개 숫자를 나열한 것으로 표현할 수 있을 것이다.
만약, 이 녹음기의 성능이 좋은 편이라 1초당 100개의 데이터를 취득해올 수 있다고 하면 총 10초 녹음했을 때 얻게 되는 데이터는 1000개 숫자를 나열한 것으로 표현할 수 있다.
(실제로 최신 녹음기는 1초당 4만개가 넘는 데이터를 취득해올 수도 있다!)
즉, 녹음해 온 신호를 벡터로 표현하자면 다음과 같이 쓸 수도 있을 것이다.
총 데이터의 길이가 $N$이라고 하면,
\[x[n] = \begin{bmatrix}x[0]\\x[1] \\ \vdots \\ x[N-1]\end{bmatrix}\]벡터의 기본 연산 편에서 소개한 바와 같이 기본 연산(상수배와 벡터 간의 덧셈)을 음성 신호는 만족한다고 볼 수 있으므로 음성 신호 역시도 벡터의 일종으로 볼 수 있으며, 이 때 위의 $x[n]$ 벡터의 차원은 $N$ 차원임을 알 수 있다.
주파수 성분 역시도 벡터
그렇다면, 우리가 그림 2에서 본 주파수 성분은 어떨까?
주파수 성분도 역시 벡터로 볼 수 있다.
이 부분은 다소 어렵게 들릴 수도 있지만,
가령 주파수 성분 벡터의 첫 번째 요소가 0Hz의 성분 값을 표현한다고 하고, 두 번째 요소가 1Hz의 성분 값을 표현한다고 하고 … 등등
이런 방식으로 적절히 주파수 대역을 나눠준다면 주파수 성분 역시도 벡터로써 표현할 수 있다.
만약, 전체 주파수 대역을 $N$개로 시간 신호의 길이와 같이 나눠준다고 하면 주파수 성분 벡터는 다음과 같이 표현할 수도 있다.
\[X[k] = \begin{bmatrix}X[0]\\X[1]\\ \vdots \\ X[N-1] \end{bmatrix}\]푸리에 변환: 시간 신호 벡터와 주파수 벡터 간의 선형변환
※ 이 꼭지는 주파수 샘플링과 DFT에서 일부 가져온 것입니다.
우리는 행렬 곱에 대한 새로운 시각편에서 행렬이란 벡터를 입력으로 받고 또 다른 벡터를 출력 해주는 함수(조금 어려운 말로 선형변환)로 작동한다고 배운 바 있다.
그런데, 우리가 그림 2에서 했던 일이 뭐였더라?
시간 신호 벡터를 주파수 벡터로 변환시켜 준 것이었다.
즉, 어떤 벡터를 다른 벡터로 변환시켜 준 것이다.
우리는 이런 일을 할 수 있는 행렬이 존재한다는 것을 직감할 수 있다.
이런 변환을 해주는 행렬을 우리는 ‘푸리에 행렬’이라고 부른다.
푸리에 행렬은 다음과 같은 이산 푸리에 변환으로부터 얻어낼 수 있다.
| DEFINITION: DFT and iDFT |
|---|
| 전체 신호의 길이가 N인 이산 신호 $x[n]$과 길이가 N인 이산 주파수 성분 $X[k]$에 대하여 |
그렇다면 신호 벡터에 어떤 행렬(여기서 푸리에 행렬)을 통해 주파수 성분 벡터를 얻었다고 볼 수 있을 것이다. 이를 알기 위해 $k=0,1,\cdots, N-1$일 때의 $X[k]$ 값을 하나하나 계산해보자.
\[X[0] = x[0]\exp\left(-j\frac{2\pi 0}{N}0\right) + x[1]\exp\left(-j\frac{2\pi 0}{N}1\right)+\cdots +x[N-1]\exp\left(-j\frac{2\pi 0}{N}(N-1)\right)\] \[=x[0]\cdot 1 + x[1]\cdot 1 + \cdots + x[N-1] \cdot 1\] \[X[1] = x[0]\exp(\left(-j\frac{2\pi 1}{N}0\right)+x[1]\exp\left(-j\frac{2\pi 1}{N}1\right)+\cdots +x[N-1]\exp(\left(-j\frac{2\pi 1}{N}(N-1)\right)\]여기서 표기의 단순화를 위해
\[w = \exp\left(-j\frac{2\pi}{N}\right)\]이라고 하자.
그러면,
\[X[1]\Rightarrow x[0]w^0 + x[1] w^1 + \cdots + x[N-1]w^{N-1}\]이런 방식으로 $i$번째 주파수 성분 $X[i]$는 다음과 같이 계산할 수 있음을 알 수 있다.
\[X[i] = x[0]w^0 + x[1]w^{i\times1}+\cdots+x[j]w^{i\times j}+\cdots +x[N-1]w^{i\times(N-1)}\]즉, 이런 과정을 거치게 되면 DFT를 다음과 같이 벡터와 행렬의 관계로 표현할 수 있다는 것을 알 수 있다.
\[\begin{bmatrix}X[0]\\X[1]\\ \vdots \\ X[N-1]\end{bmatrix} = \begin{bmatrix} 1 && 1 && 1 && \cdots && 1 \\ 1 && w^1 && w^2 && \cdots && w^{N-1} \\ \vdots && \vdots && \vdots && \ddots && \vdots \\ 1 && w^{N-1} && w^{(N-1)\cdot 2} && \cdots && w^{(N-1)\cdot(N-1)}\end{bmatrix}\begin{bmatrix}x[0]\\x[1]\\ \vdots \\ x[N-1]\end{bmatrix}\]행렬과 선형변환편에서는 행렬이 일종의 선형변환이라고 말했고,
행렬 곱에 대한 또 다른 시각편에서는 일반적인 행렬의 곱은 왼쪽에 곱해지는 행렬의 행과 오른쪽에 곱해지는 행렬의 한 열 간의 내적이라고 말한 바 있다.
또, 내적의 의미는 ‘닮음’이기도 한데, 그 말인 즉슨, 신호 벡터에 푸리에 행렬을 곱해준다는 것은 푸리에 행렬의 행과 신호 벡터가 얼마나 닮았는지를 확인해봄으로써 주파수 성분을 얻을 수 있다는 것을 말한다고 할 수 있다.
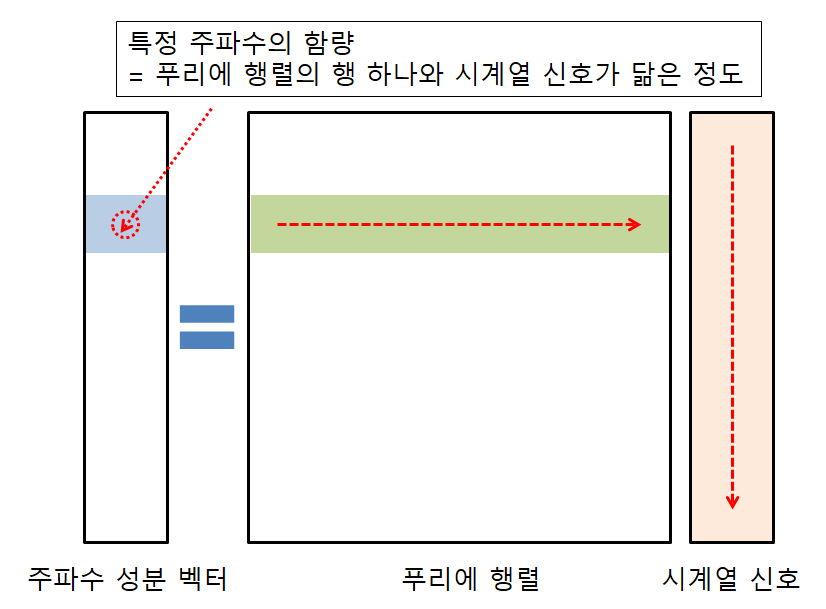
그림 3. 주파수 성분 벡터는 푸리에 행렬의 행과 시계열 벡터가 얼마나 닮았는지를 봄으로써 얻을 수 있는 것이다.
그렇다면, 푸리에 행렬의 각각의 행이 가져다주는 의미는 무엇일까?
푸리에 행렬이 가져다주는 의미
오일러 공식의 기하학적 의미편에서는 아래와 같은 공식의 의미에 대해 다룬 적이 있다.
\[e^{j\theta}=\cos(\theta) + j\sin(\theta)\]식 (12)의 의미를 파악하기 위해 우변의 값을보면, 이는 복소평면에서 원점으로부터 $\theta$ 라디안만큼 회전한 호(弧, arc)의 좌표를 의미한다는 것을 알 수 있다.
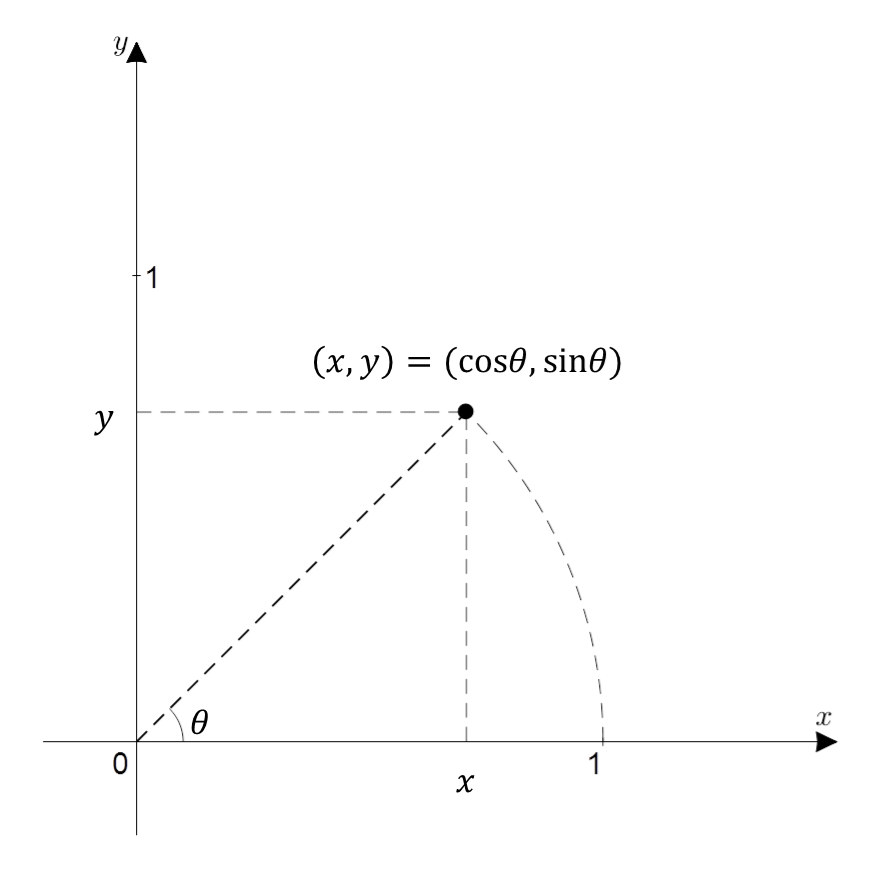
그림 4. 복소 평면 상에서 표현한 $x+iy$. 삼각함수로 표현하면 $x$축으로부터의 각도를 $\theta$ 라디안이라 했을 때 $\cos\theta + i \sin\theta$이다.
다시 말해 식 (8)에 있는 $w$는 다음과 같이 계산하는데,
\[w = \exp\left(-j\frac{2\pi}{N}\right)\]이 말인 즉슨, 시계 방향으로 한 바퀴 도는 원 위의 점을 $N$ 등분 한 첫 번째 점의 위치라는 의미이다.
이와 같은 $w$의 의미를 생각하면서 $N=8$인 경우의 푸리에 행렬을 예시로 그 의미를 확인해보자.
$N=8$인 경우 푸리에 행렬에 들어가는 $w$의 값은 $w=\exp\left(-j\frac{2\pi}{8}\right)$이다. 이것을 복소평면에 표시하면 다음과 같다.
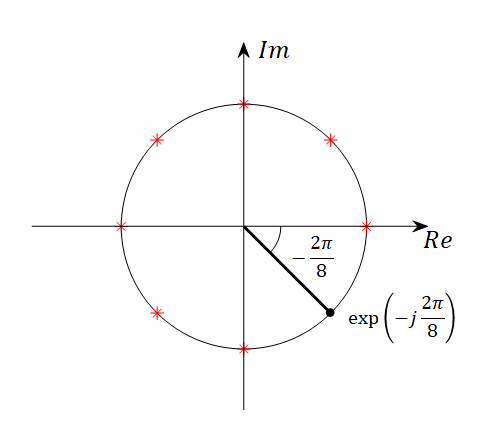
그림 5. $\exp(-j 2\pi/8)$을 복소평면 상에 표시한 것. 빨간색 별표는 w의 0승, 2승, 3승, ..., 7승을 표시한 것.
그림 5과 같이 $w$의 복소평면의 단위원 위의 phase로 푸리에 행렬 내의 복소수를 그림으로 대체하면 아래의 그림 6와 같을 것이다.
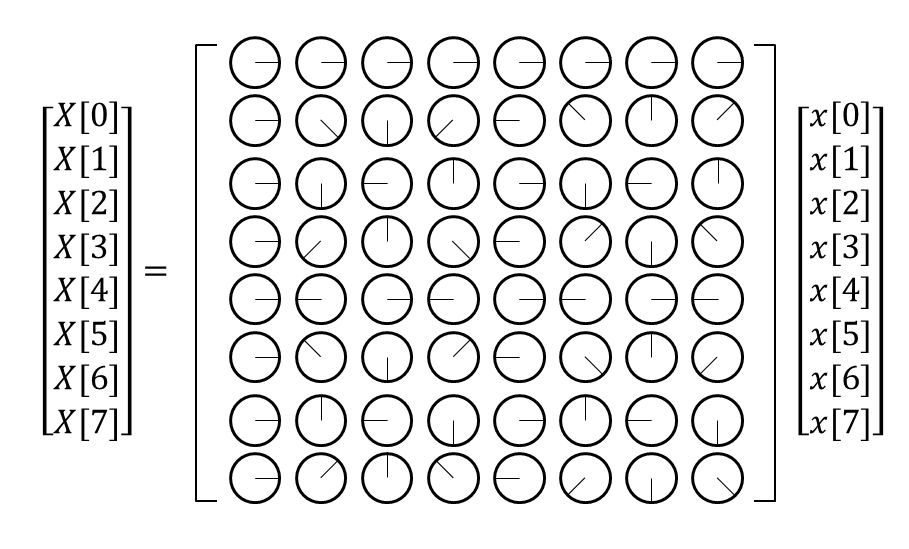
그림 6. $N=8$인 경우의 푸리에 행렬을 시각화 한 것. 푸리에 행렬 내의 그림은 복소수 $w$가 가르키는 phase를 표시하였다.
cosine 함수나 sine 함수 모두 원의 회전으로부터 출발하는 개념이므로 회전시 phase의 값은 모두 cosine 혹은 sine 함수의 값으로 바꿔 생각해볼 수 있다.
따라서 푸리에 행렬의 phase를 cosine 함수에 대해 생각해보면 다음과 같이 생각할 수 있다.
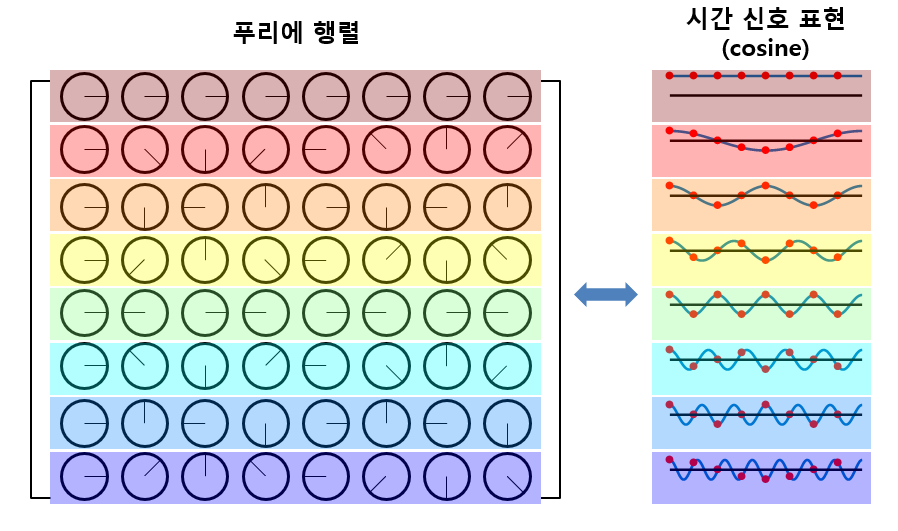
그림 7. 푸리에 행렬 내의 각 복소수 원소들의 phase를 cosine 함수로 치환해 생각해본 경우
위의 그림 7에서 볼 수 있듯이 푸리에 행렬의 각 행은 주파수 0에서부터 fundamental frequency의 배수만큼의 cosine 함수를 표현하고 있는 것을 알 수 있다.
또, 푸리에 행렬의 phase를 sine 함수에 대해 생각해보면,
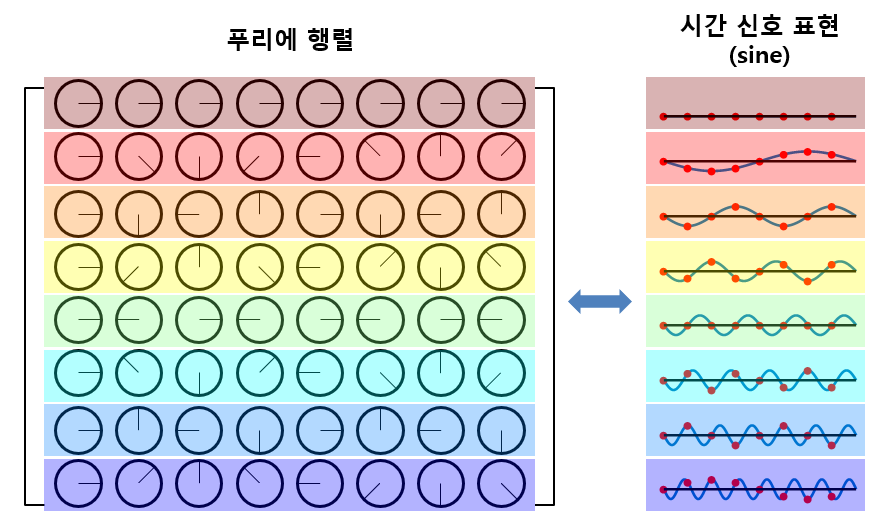
그림 8. 푸리에 행렬 내의 각 복소수 원소들의 phase를 sine 함수로 치환해 생각해본 경우
위의 그림 8에서 볼 수 있듯이 푸리에 행렬의 각 행은 주파수 0에서부터 fundamental frequency의 배수만큼의 sine 함수도 함께 표현하고 있는 것을 알 수 있다.
즉, DFT를 계산할 때 사용하는 푸리에 행렬은 fundamental frequency의 배수로 구성된 cosine, sine 함수들이며, 이 함수들이 실수부와 허수부를 구성하며, 원래의 시간 신호와 하나 하나 내적되어 결과를 얻어주는 것이다.
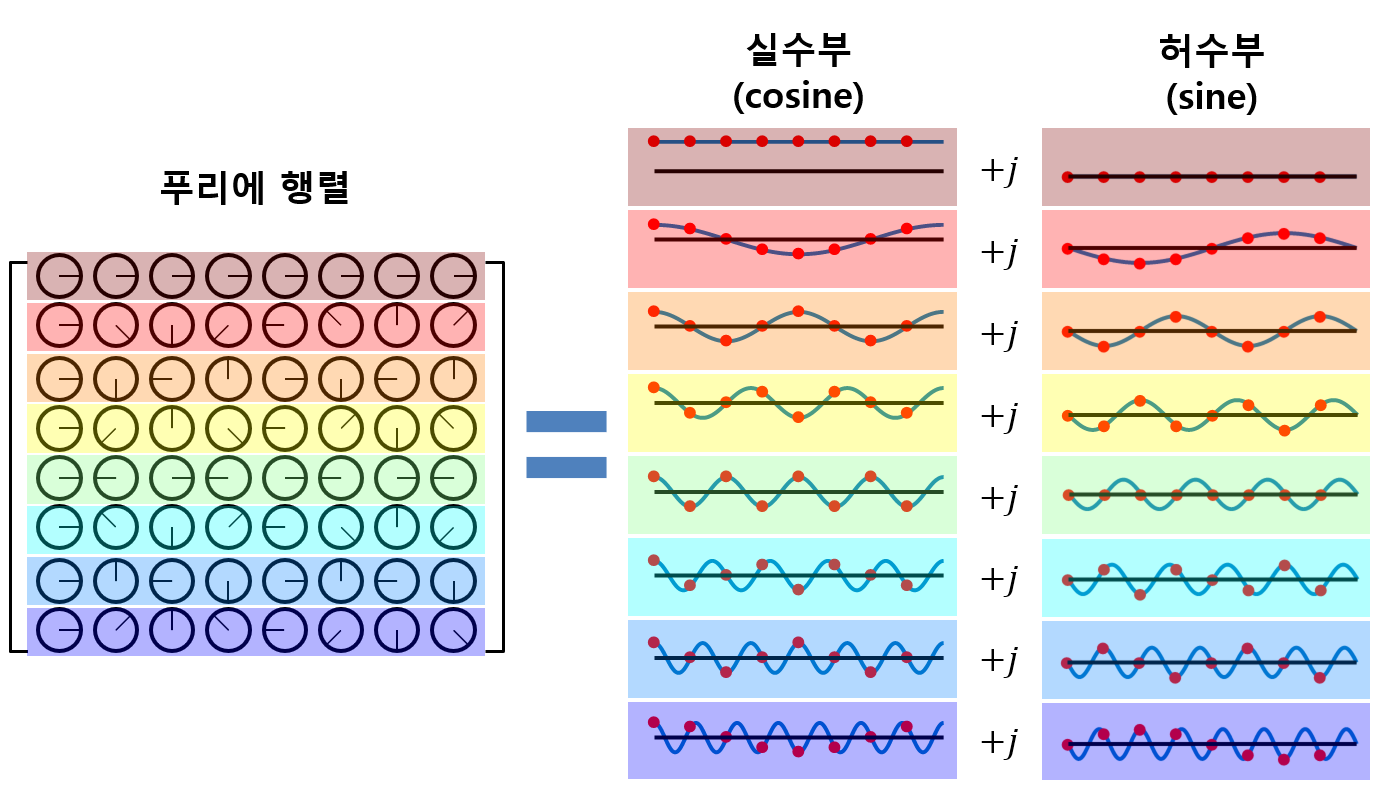
그림 9. 푸리에 행렬 내의 값들은 모두 복소수이며, 실수부와 허수부는 각각 cosine, sine 함수로 구성되어 있다는 것을 알 수 있다.
푸리에 행렬의 특성
이번에는 푸리에 행렬의 특성을 파악해보자.
1. 푸리에 행렬의 열들은 서로 직교함
우리는 간단한 방법으로 푸리에 행렬의 각 열들이 직교한다는 것을 확인할 수 있다.
가장 쉬운 방법으로는 푸리에 행렬 $F$에 Hermitian 연산1을 취한 뒤 곱해보는 것이다.
즉,
\(F^HF = \begin{bmatrix} 1 && 1 && 1 && \cdots && 1 \\ 1 && w^{*1} && w^{*2} && \cdots && w^{*(N-1)} \\ \vdots && \vdots && \vdots && \ddots && \vdots \\ 1 && w^{*(N-1)} && w^{*(N-1)\cdot 2} && \cdots && w^{*(N-1)\cdot(N-1)}\end{bmatrix}\times\notag\) \(\begin{bmatrix} 1 && 1 && 1 && \cdots && 1 \\ 1 && w^1 && w^2 && \cdots && w^{N-1} \\ \vdots && \vdots && \vdots && \ddots && \vdots \\ 1 && w^{N-1} && w^{(N-1)\cdot 2} && \cdots && w^{(N-1)\cdot(N-1)}\end{bmatrix}\)
\[=N\begin{bmatrix}1 && 0 && \cdots && 0 \\ 0 && 1 && \cdots && 0 \\ \vdots && \vdots && \ddots && \vdots \\ 0 && 0 && \cdots && 1\end{bmatrix} = N\cdot I\]여기서 superscript ‘*‘은 complex conjugate이다.
이를 확인하기 위해 $F^HF$의 계산 결과의 $m$ 번째 행, $n$ 번째 열을 생각해보자.
\[F^H_{m,:}F_{:,n} = \begin{bmatrix}1 & w^{*\cdot m \cdot 1} & \cdots & w^{*\cdot m \cdot (N-1)}\end{bmatrix}\cdot \begin{bmatrix}1\\w^{1\cdot n} \\ \vdots \\ w^{(N-1)\cdot n}\end{bmatrix}\] \[=1+w^{*\cdot m\cdot 1}w^{1\cdot n}+\cdots+w^{*\cdot m\cdot (N-1)}w^{(N-1)\cdot n}\] \[=\sum_{k=0}^{N-1}w^{*m\cdot k}w^{k\cdot n}\] \[=\sum_{k=0}^{N-1}\exp\left(j\frac{2\pi}{N}m\cdot k\right)\exp\left(-j\frac{2\pi}{N}n\cdot k\right)\] \[=\sum_{k=0}^{N-1}\exp\left(j\frac{2\pi}{N}(m-n)\cdot k\right)\]따라서 $m=n$인 경우 $F^H_{m,:}F_{:,n}=N$이고, $m\neq n$인 경우 $F^H_{m,:}F_{:,n}=0$이다.
식 (15)의 결과와 같이 푸리에 행렬 $F$의 각 열들은 각 열 자신과 내적 시에는 $N$이라는 값을 갖고 이외의 열과 내적했을 때는 0이라는 결과를 얻어주게 되므로, 각각의 열들은 서로 직교한다는 것을 알 수 있다.
2. 푸리에 행렬의 역행렬과 역푸리에 변환
또, 식 (14)과 식 (15)를 통해 푸리에 행렬의 역행렬은
\[F^{-1}=\frac{1}{N}F^H\]라는 것을 알 수 있다.
즉,
\[\begin{bmatrix}x[0]\\x[1]\\ \vdots \\ x[n-1]\end{bmatrix} = \frac{1}{N}\begin{bmatrix} 1 && 1 && 1 && \cdots && 1 \\ 1 && w^{*1} && w^{*2} && \cdots && w^{*(N-1)} \\ \vdots && \vdots && \vdots && \ddots && \vdots \\ 1 && w^{*(N-1)} && w^{*(N-1)\cdot 2} && \cdots && w^{*(N-1)\cdot(N-1)}\end{bmatrix}\begin{bmatrix}X[0]\\X[1]\\ \vdots \\ X[N-1]\end{bmatrix}\]이며, 이것은 inverse DFT의 식과 같다는 것 또한 쉽게 알 수 있을 것이다.
3. 역 푸리에 변환이 말해주는 것
행렬 곱에 대한 새로운 시각 편에서 열공간에 기반한 해석 파트를 다시 한번 생각해보자.
예를 들어 아래와 같은 행렬은,
\[\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}3\\5\end{bmatrix}\]연립방정식을 풀면 쉽게 알 수 있다.
\[\begin{cases} x+2y = 3 \\ 3x+4y = 5 \end{cases}\] \[\Rightarrow x=-1, \text{ }y=2\]하지만, 이번엔 이 식을 아래와 같이 생각해보자.
\[x\begin{bmatrix}1\\3\end{bmatrix}+y\begin{bmatrix}2\\4\end{bmatrix}=\begin{bmatrix}3\\5\end{bmatrix}\]위 식에 대한 해석은 아래와 같이 할 수도 있다고 행렬 곱에 대한 새로운 시각 편에서 언급한 바가 있다.
이 얘기를 푸리에 행렬에 그대로 적용해본다면 우리가 역 푸리에 변환을 취해준다는 것의 의미는 다음과 같다.
“N개의 $F^{-1}$의 열벡터로 생성된 벡터 공간 내에 $N$ 차원 시계열 벡터가 존재하는가?”
“그렇다면 $F^{-1}$의 열벡터를 어떻게 조합해야 시계열 벡터를 만들 수 있는가?”
즉, 무슨 말인가?
즉, 모든 시계열들은 정현파의 합으로 구성할 수 있으며, 정현파를 어떻게 조합하는가에 따라 시계열의 형태가 달라진다는 것을 다시 한번 방증하는 것이다.
-
Hermitian 연산자 = Transpose + complex conjugate 이다. ↩