Prerequisitess
본 포스팅을 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
2계 제차 선형 미분방정식
2계 선형 미분방정식이란 아래와 같이 미분계수의 최고 미분횟수가 2회인 미분방정식을 의미한다.
\[a(t)\frac{d^2x}{dt^2} + b(t)\frac{dx}{dt} + c(t)x(t) = g(t) % 식 (1)\]이번 시간에는 특별히 $a(t)$, $b(t)$, $c(t)$가 모두 상수이고 $g(t)=0$인 2계 제차 선형 미분방정식에 대해 다루고자 한다.
다시 말해 우리가 다루고자 하는 미분방정식의 꼴은 아래와 같다.
\[a\frac{d^2x}{dt^2}+b\frac{dx}{dt}+cx(t) = 0 % 식 (2)\]여기서 $a$는 0이 아니어야 한다.
선형 연립 미분방정식을 이용한 해법
우리는 사실 2계 제차 선형 미분방정식의 해법에 대해 다룬 적이 있다.
연립 미분방정식 모델링 편에서 damped harmonic oscillation을 다룰 때 이 해법을 언급한 적이 있다.
2계 제차 선형 미분방정식의 해법은 1차 미분계수 $dx/dt$를 새로운 변수로 놓고 풀어주는 것이 핵심이다.
식 (2)와 같은 2계 제차 선형 미분방정식에 대해서 우리는 다음과 같이 생각할 수 있다.
만약,
\[y=\frac{dx}{dt} % 식 (3)\]와 같은 새로운 변수를 생각한다면,
\[\frac{dy}{dt}=\frac{d}{dt}\left(\frac{dx}{dt}\right)=\frac{d^2x}{dt^2} % 식 (4)\]이므로,
식 (2)는 다음과 같이 쓸 수도 있을 것이다.
\[a\frac{dy}{dt}+by+cx = 0 % 식 (5)\] \[\Rightarrow \frac{dy}{dt}=-\frac{b}{a}y-\frac{c}{a}x % 식 (6)\]다시 한번 $x$와 $y$에 대한 연립 미분방정식으로 이 과정을 풀어서 생각하면 다음과 같다.
\[\begin{cases}\dfrac{dx}{dt}=y \\\\ \dfrac{dy}{dt}=-\dfrac{c}{a}x-\dfrac{b}{a}y\end{cases} % 식 (7)\]그러므로 식 (2)의 2계 제차 선형 미분방정식은 다음과 같이 행렬의 꼴로 항상 나타낼 수 있다.
\[\begin{bmatrix}dx/dt \\ dy/dt \end{bmatrix} = \begin{bmatrix}0 & 1 \\ -c/a & -b/a\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} % 식 (8)\]여러번 강조하는 것 같지만 식 (8)에서 $a$는 0이 아니어야 한다.
여기서 알 수 있게 되는 것은 식 (8)을 풀게 됨으로써 2계 제차 선형 미분방정식의 solution을 얻어낼 수 있다는 것이다.
선형 연립 미분방정식으로 해를 구하는 것의 의미
선형 연립 미분방정식으로 만들어 2계 제차 미분방정식의 해를 구할 수 있다는 것은 위상 평면편 에서 보았던 것 처럼 식 (8)에 있는 행렬의 고윳값, 고유벡터를 이용하는 것이 solution을 구하는 연결고리가 된다는 점을 시사하기도 한다.
우리는 식 (8)에 들어있는 행렬의 고윳값, 고유벡터를 구해 연립 미분방정식의 솔루션을 구해보도록 하자.
식 (8)에 들어있는 행렬에 대한 특성방정식을 구해보면 다음과 같다.
\[\text{det}\left(\begin{bmatrix}0-\lambda & 1 \\ -c/a & -\frac{b}{a}-\lambda \end{bmatrix}\right)\] \[=-\lambda\left(-\frac{b}{a}-\lambda\right)+\frac{c}{a}\] \[=\lambda^2 +\frac{b}{a}\lambda+\frac{c}{a}=0\]여기서 2차 방정식의 근의 공식을 이용해 특성방정식의 해를 구하면 다음과 같음을 알 수 있다.
\[\lambda =\frac{-b/a\pm\sqrt{\left(b/a\right)^2-4(c/a)}}{2}\] \[=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]그리고 고유벡터를 구하면 다음과 같음을 알 수 있다.
\[v_1 = \begin{bmatrix}1\\-(b+\sqrt{b^2-4ac})/2a\end{bmatrix}=\begin{bmatrix}1\\ \lambda_1\end{bmatrix}\] \[v_2 = \begin{bmatrix}1\\-(b-\sqrt{b^2-4ac})/2a\end{bmatrix}=\begin{bmatrix}1\\ \lambda_2\end{bmatrix}\]따라서, 연립 미분방정식의 일반해 공식에 따라 솔루션을 써보면,
\[\begin{bmatrix}x(t)\\y(t)\end{bmatrix}=c_1e^{\lambda_1 t}\begin{bmatrix}1 \\ \lambda_1\end{bmatrix}+c_2e^{\lambda_2 t}\begin{bmatrix}1 \\ \lambda_2\end{bmatrix}\]이다. 여기서 $c_1$, $c_2$는 임의의 상수이며 $\lambda_{1,2}$는
\[\lambda_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\]이다.
우리는 2계 미분방정식을 풀 때 $y=dx/dt$로 놓고 풀기 때문에 식 (16)의 $x(t)$ 부분 만을 얻어오면 그것이 2계 미분방정식의 solution이 되는 것이다.
그러므로 2계 제차 선형미분방정식의 솔루션 $x(t)$는 다음과 같다.
\[x(t)=c_1e^{\lambda_1 t}+c_2e^{\lambda_2 t}\]예시 문제
이론 설명만으로는 이해하기 어려울 수도 있으니 2계 제차 미분방정식 예시 문제를 직접 풀어보도록 하자.
아주 간단한 예시로 문제 풀이를 해보자. 아래의 2계 제차 미분 방정식의 해를 구해보자.
\[\frac{d^2x}{dt^2}-4\frac{dx}{dt}+3x(t) = 0 % 식 (13)\]우리는 이 문제를 풀기 위해 2계 미분방정식을 연립 미분방정식으로 바꿔보자.
그러기 위해 다음과 같은 새로운 변수 $y(t)$를 생각해보자.
\[y(t) = \frac{dx}{dt}\]그러면
\[\frac{dy}{dt}=\frac{d^2x}{dt^2} = 4\frac{dx}{dt}-3x(t)\]과 같은 관계를 얻을 수 있다.
따라서, 우리는 아래와 같은 연립 미분방정식을 도출할 수 있게 된다.
\[\begin{cases}\dfrac{dx}{dt} = y\\\\ \dfrac{dy}{dt}=-3x+4y\end{cases}\] \[\Rightarrow \begin{bmatrix}dx/dt \\ dy/dt\end{bmatrix} = \begin{bmatrix}0 & 1 \\ -3 & 4\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix}\]이제 우리는 식 (23)에 있는 행렬의 고윳값과 고유벡터를 얻어보도록 하자.
고윳값, 고유벡터의 정의에 따라, 고유벡터가 $\vec{v}$라고 하고 고윳값이 $\lambda$라고 했을 때 다음 식을 만족해야 한다.
\[\begin{bmatrix}0 & 1 \\ -3 & 4 \end{bmatrix}\vec{v} = \lambda\vec{v}\]모든 항을 왼쪽으로 이항하면,
\[\begin{bmatrix}0-\lambda & 1 \\ -3 & 4-\lambda\end{bmatrix}\vec{v} = 0\]$\vec{v}$가 영벡터가 되지 않기 위해선 식 (25)의 행렬이 역행렬을 가지면 안되기 때문에 아래의 조건을 만족해야 한다. (이것을 특성방정식이라고도 부른다.)
\[det\left(\begin{bmatrix}0-\lambda & 1 \\ -3 & 4-\lambda\end{bmatrix}\right) = 0\] \[=\lambda(\lambda-4)+3\] \[=\lambda^2 - 4 \lambda + 3 = 0\]따라서, 고윳값은
\[\lambda = 1 \text{ or } 3\]이다.
각 고윳값에 해당하는 고유벡터를 찾아보면, 식 (25)로부터
$\lambda = 1$인 경우,
\[식(26) \Rightarrow\begin{bmatrix}0 -1 & 1 \\ -3 & 4-1 \end{bmatrix}\vec{v} = \lambda\vec{v}\] \[=\begin{bmatrix}-1 & 1 \\ -3 & 3\end{bmatrix}\begin{bmatrix}v_1 \\ v_2\end{bmatrix}\] \[=\begin{bmatrix}-v_1 + v_2 \\ -3 v_1 + 3v_2 \end{bmatrix}=\begin{bmatrix}0 \\ 0\end{bmatrix}\] \[\therefore \vec{v} = \begin{bmatrix}1 \\ 1\end{bmatrix}\]또, $\lambda = 3$인 경우,
\[식(26) \Rightarrow\begin{bmatrix}0 -3 & 1 \\ -3 & 4-3 \end{bmatrix}\vec{v} = 0\] \[= \begin{bmatrix}-3 & 1 \\ -3 & 1 \end{bmatrix}\begin{bmatrix}v_1 \\ v_2\end{bmatrix} = 0\] \[= \begin{bmatrix}-3 v_1& v_2 \\ -3v_1 & v_2 \end{bmatrix}\vec{v} = \begin{bmatrix}0 \\ 0\end{bmatrix}\] \[\therefore \vec{v} = \begin{bmatrix}1 \\ 3\end{bmatrix}\]따라서, 식 (23)의 일반해는
\[\begin{bmatrix}x(t) \\ y(t) \end{bmatrix} = c_1\begin{bmatrix}1 \\ 1\end{bmatrix}e^t + c_2 \begin{bmatrix}1 \\3 \end{bmatrix}e^{3t}\]이다.
그러므로, 식 (19)의 일반해는
\[x(t) = c_1e^t + c_2e^{3t}\]이다.
참고로 식 (23)에 대한 위상평면을 그려보면 다음과 같다. 굵은 검은색 선은 고유벡터를 따라가는 직선이다.
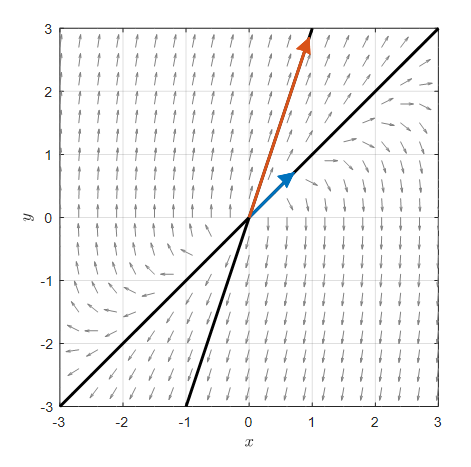
그림 2. 식 (23)의 연립 미분방정식에 관한 위상 평면. 굵은 검은색 선은 고유벡터를 따라가는 직선임.