Prerequisites

본 포스팅을 더 잘 이해하기 위해서는 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 표본과 표본 통계량
• 스튜던트의 t-test
• 귀무가설

Motivation

두 그룹 간에 통계적으로 유의한 차이가 있는지 확인해보고 싶을 때가 있다.

그런데 어떤 경우에는 기존의 모수 통계 기법을 이용하기 어려운 경우가 있다. 이럴 때 우리는 비모수 검정법 중 하나인 순열 검정법(permutation test)을 고려해볼 수 있다.

모수 통계 기법의 가장 큰 장점은 모수(parameters)만을 이용해서 문제를 풀어나갈 수 있다는 점이다.

그런데, 그러기 위해선 표본의 모집단 혹은 통계량의 분포를 잘 알고 있다는 가정이 필요하다¹. 만약 이 조건을 만족하지 못하면 우리는 모수통계기법을 사용할 수 없다.

이에 반해 비모수 통계 기법 중 순열 검정(permutation test)을 이용하면 데이터의 모집단 분포가 정규분포를 따르지 않거나 특이한 통계량을 사용하더라도 표본 집단간 비교를 수행할 수 있다.

이번 포스팅에서는 순열 검정의 배경 이론과 실제적인 사용 방법에 대해 알아보도록 하자.

순열 검정의 배경 이론과 절차

순열 검정의 귀무가설

순열 검정의 배경 이론을 이해하기에 앞서 ‘두 그룹 간 차이가 있다’라고 말하는 것이 어떤 것을 말하는지 다시 한번 복습해보도록 하자.

귀무가설, t-test 등을 공부하면서 귀에 딱지가 앉게 듣는 말이 있다.

바로,

"두 표본 집단이 하나의 모집단에서 나왔다고 하자"

는 “귀무가설”이다. 이번에는 기존의 접근법과는 조금 다르게 위 문구를 조금 다르게 관찰해서 그림으로 표현하면 아래와 같이 볼 수도 있다.

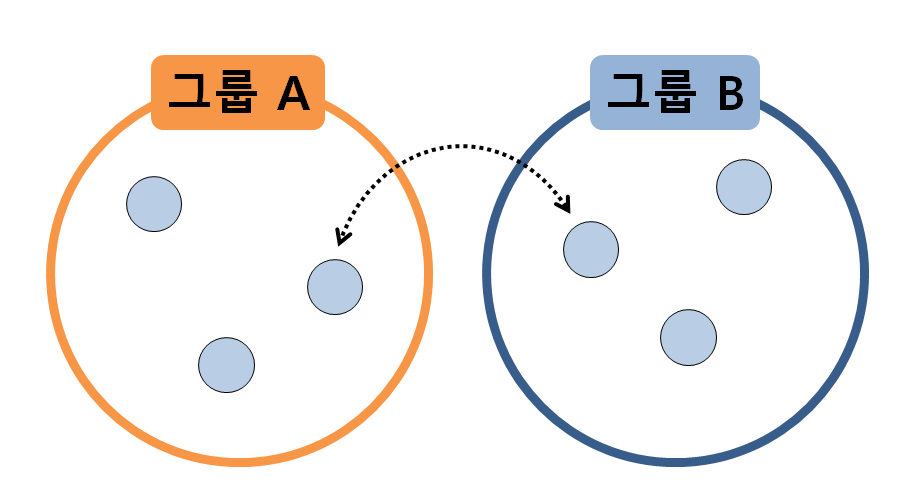
그림 1. 두 표본 그룹이 동일한 모집단에서 추출되었다고 볼 수 있는 경우

위 그림은 모든 표본이 같은 값이라는 부분은 많이 과장되어 있지만, 본질적으로 짚고자 하는 내용은 다음과 같다.

만약 두 표본 그룹이 동일한 모집단에서 추출되었다고 한다면, 두 그룹 안에 있는 샘플들을 교환한 뒤 통계적으로 검증해도 여전히 두 그룹간에는 차이가 없어야 한다.

이 부분이 순열 검정(permutation test)를 생각해내는 가장 핵심적인 귀무가설이다. 교과서에 있는 표현을 빌려 이름을 붙이면 null hypothesis of exchangeability라고 할 수 있다.

즉, 정말로 두 그룹의 샘플들이 동일한 모집단에서 나왔다고 한다면 샘플들을 교환해서 통계량을 계산하더라도 두 그룹간의 차이를 볼 수 없어야 한다는 것이다.

그런데, 만약 아래 그림과 같이 두 표본 그룹이 전혀 다른 모집단에서부터 추출되었다면 샘플 간 교환을 수행할 때 통계량의 산출값이 많이 바뀔 것이라는 것을 예상할 수 있다.

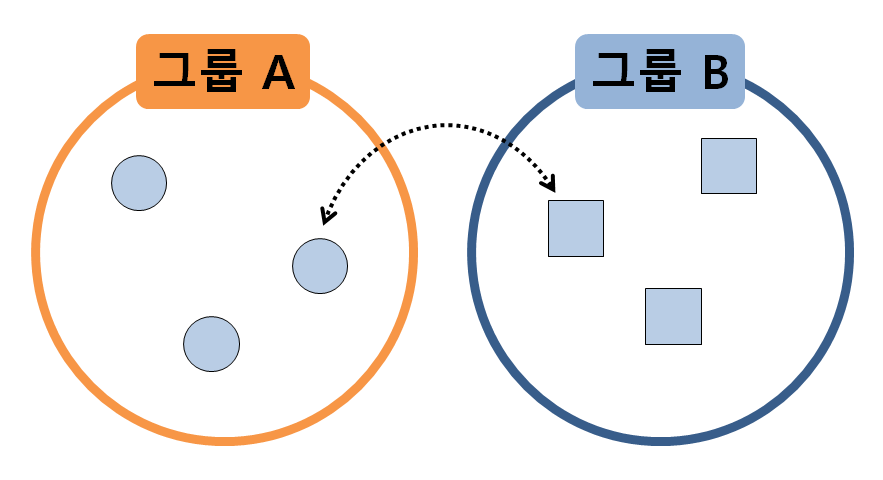
그림 2. 두 표본 그룹이 다른 모집단에서 추출된 경우

그래서 우리는 샘플들을 섞어가면서 통계량을 여러번 추출할 것이다.

그리고 추출된 통계량들의 값의 분포를 확인해보면 원래 주어진 데이터에서 계산한 통계량이 얼마나 큰 값인지 유추해볼 수 있을 것이다.

순열 검정의 사용 절차

우리는 이제부터 샘플들을 한 쌍 씩 섞어주는 것이 아니라 무작위로 섞은 뒤 그룹을 나눌 것이다. 다시 말해 원래의 데이터들을 순서는 고려한 채 선별하겠다는 의미이다.

이 개념이 바로 고등학교 확률 시간에 배우는 순열(permutation)이다. 그런 다음 통계량을 계산하고 histogram을 그려보자.

물론 이렇게 말로만 적으면 바로 이해하기 어렵기 때문에 차근히 예시를 들어가며 이해해보도록 하자.

우리에게 다음과 같이 두 그룹의 샘플 데이터가 주어져 있다고 생각해보자.

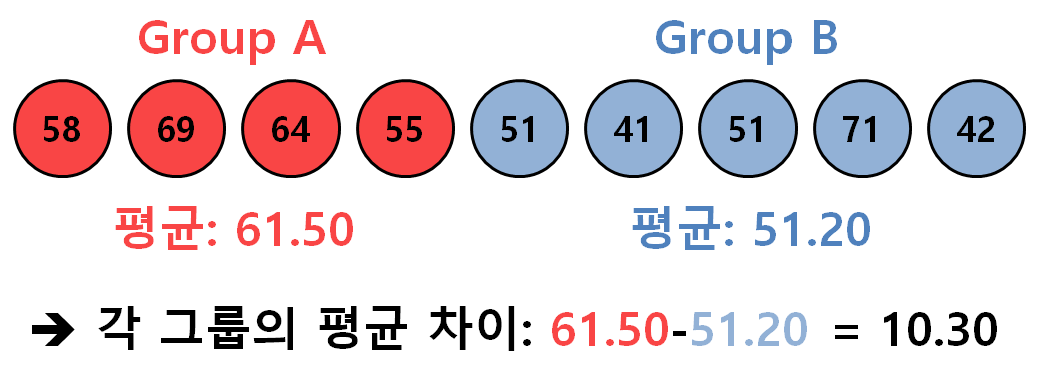
그림 3. 주어진 두 그룹의 샘플 데이터와 관찰하고자 하는 통계량(평균의 차이)

우리가 여기서 알고싶은 것은 두 그룹 평균의 차이인 10.30이 과연 통계적으로 유의하게 크다고 말할 수 있는 값인가 하는 것이다.

(즉, 여기서는 통계량으로 두 그룹의 평균값 차이를 이용했다. 필요한 경우 다른 통계량을 얼마든지 사용해도 된다.)

각 그룹 별 샘플들이 어떤 모집단에서 나왔는지 알 수 없을 뿐더러 샘플 수가 너무 적다보니 중심극한정리를 적용하기도 어려우므로 모수 검정을 사용하는 것은 어려움이 있다.

따라서, 본 포스팅의 목적에 따라 순열 검정을 사용해보자.

최종적인 목적은 통계량의 분포를 만들고 우리가 관찰한 평균값의 차이인 10.30이 분포에서 어느정도 큰 값인지 확인하는 것이다.

그래서 우리는 분포를 만들기 위해 아래와 같이 원래 주어진 샘플 데이터들을 다음과 같이 선택해보자.

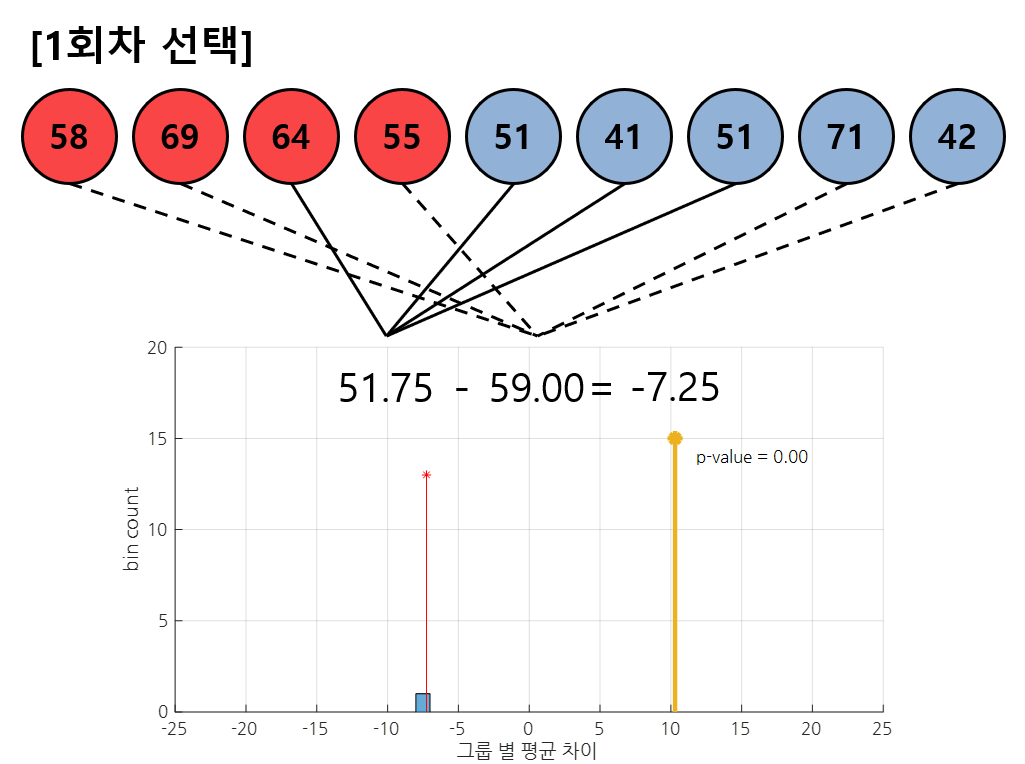
그림 4. 1회차 셔플링에서는 데이터 [3, 5, 6, 7], [1, 2, 4, 8, 9] 번이 선택되었다.

순열 검정에서는 데이터를 여러 회 셔플링 해주면서 그 때마다 나오는 통계량을 히스토그램으로 계속 그려나간다. 그림 4에서는 1회차에서 획득된 셔플링 결과이다.

이 결과를 보면 데이터 [3, 5, 6, 7] 번이 첫 번째 그룹으로 배정되고, [1, 2, 4, 8, 9] 번이 두 번째 그룹으로 배정되면서 새로 배정된 그룹들의 평균값 차이를 계산할 수 있게 된다.

이 평균값은 그림 4의 아랫부분에서 처럼 histogram으로 하나 count해서 그린다.

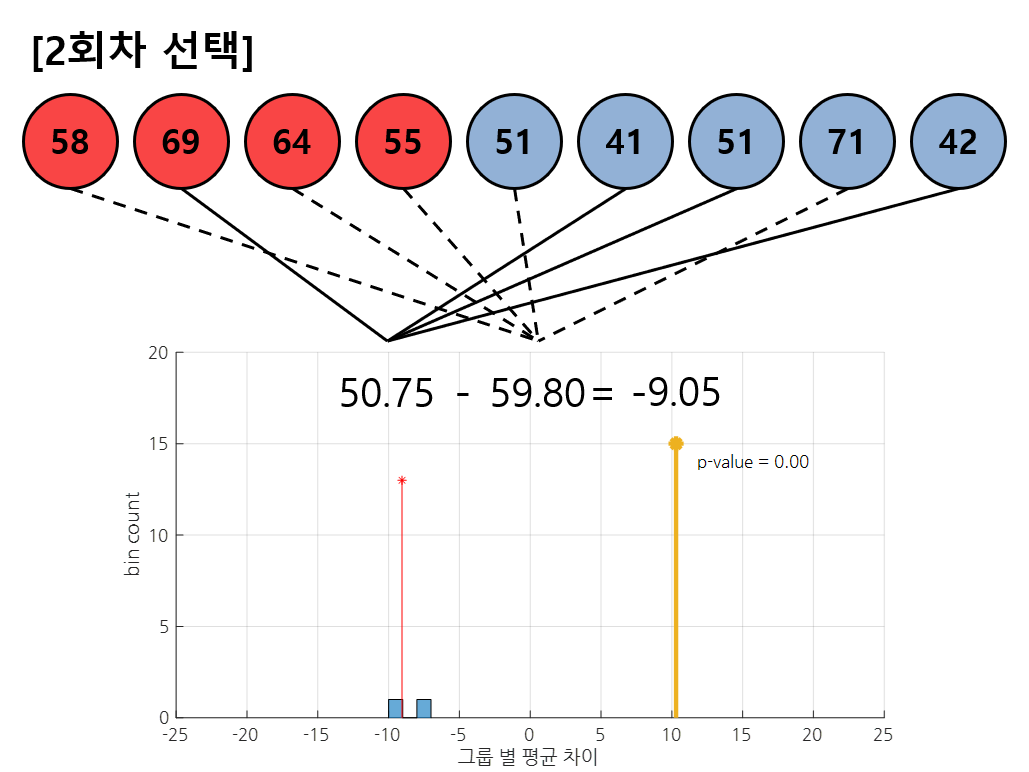
그림 5. 2회차 셔플링에서는 데이터 [2, 6, 7, 9], [1, 3, 4, 5, 8] 번이 선택되었다.

그림 5에서는 2회차 셔플링 결과를 보여준다. 이 때도 1회차에서와 마찬가지로 랜덤하게 그룹별로 샘플들이 배정된다. 새로 배정된 그룹들의 평균값 차이를 histogram으로 계속해서 추가해준다.

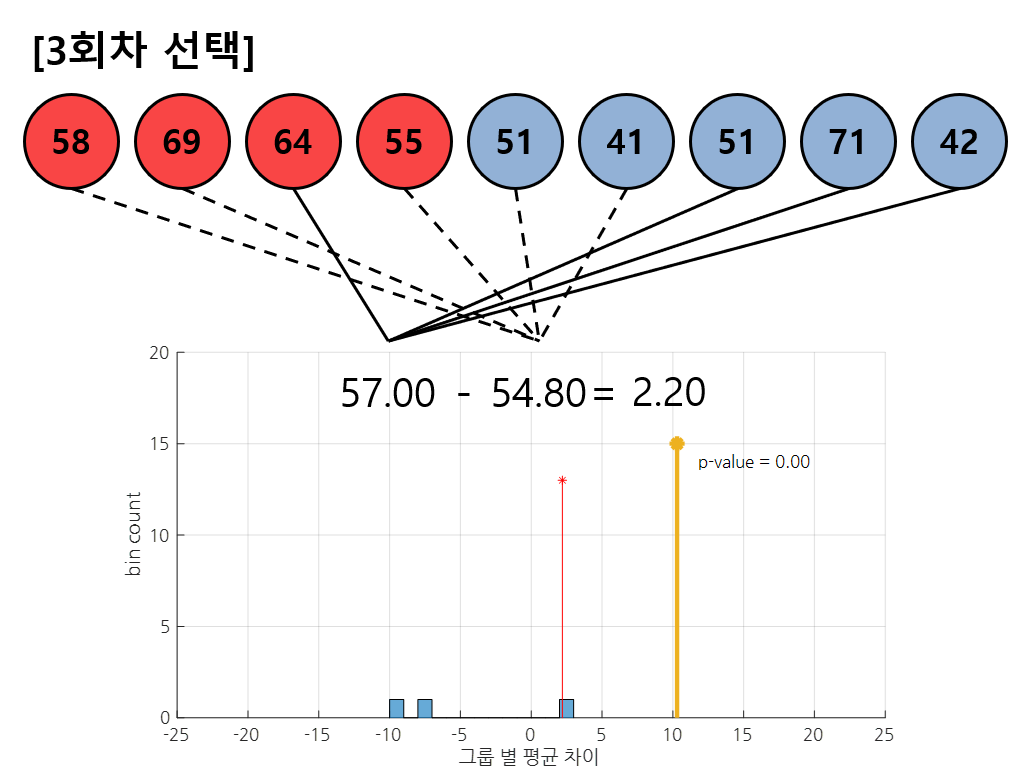
그림 6. 3회차 셔플링에서는 데이터 [3, 8, 7, 9], [1, 2, 4, 5, 6] 번이 선택되었다.

그림 6에서는 3회차 셔플링 결과를 보여주고 있다. 1, 2회차에서와 마찬가지로 랜덤하게 배정된 샘플들의 그룹별로 평균값 차이를 계산해 histogram으로 그려주자.

그림 4-6에서 수행하는 일들을 여러번 반복해주면 아래 영상과 같이 분포를 얻을 수 있게 된다.

아래 영상에서는 총 100회 셔플링을 수행해준 결과를 보여주고 있다.

그림 7. 100회차까지 셔플링을 수행하여 얻게된 permutation 분포
이 그림은 Wikipedia의 permutation test 란에 있는 그림을 수정해 만들었습니다.

마지막으로 우리에게 주어졌던 10.30이라는 값이 얼마나 permutation 분포 상에서 높은 위치를 차지하고 있는지 확인해보기 위해 p-value를 계산해보자.

p-value는 셔플링 결과로 나온 데이터 중 10.30보다 큰 값의 개수와 전체 셔플링 횟수의 비율을 가지고 계산했다.

가령, 셔플링 결과가 다음과 같이 13개가 있었다고 하면,

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]

10.30보다 큰 숫자는 11, 12, 13이고 전체 셔플링 횟수는 13이므로,

\[3/13=0.2308\]

이라는 값을 p-value로 상정했다.

Bootstrap과의 차이점?

이전 블로그 포스팅 중 Bootstrap에 관한 포스팅이 있었다.

부트스트랩도 permutation test와 유사하게 추정량(estimator)에 대한 분포를 확인하게 해주는 비모수통계 기법이다.

차이가 있다면 크게 두 가지로 볼 수 있을 것 같다. 목적에 맞게 적절한 방법을 선택하도록 하자.

1. Bootstrap은 estimator의 Confidence interval을 확인하기 위한 목적으로 주로 사용되는 반면 Permutation test는 null hypothesis를 test하기 위해 만들어졌다.
2. 수행 과정 상에서는 Bootstrap은 중복을 허용하는 resampling을 수행하는 반면 permutation test는 중복없는 재배열을 수행한다는 차이점이 있다.

참고 문헌

• Mass univariate analysis of event-related brain potentials/field I: A critical tutorial review, David M. Groppe et al., Psychophysiology, 2011
• StackExchange: bootstrap vs permutation hypothesis test