본 포스팅은 IIT의 S. C. Duta Roy 교수님의 강의를 정리한 것임을 먼저 밝힙니다.
목표
-
Normalized Lowpass Filter의 개념에 대해서 이해한다.
-
Filter간의 Transformation에 대하여 이해한다.
-
Bandpass Filter 또는 Bandstop Filter의 기하평균적 특징(Geometrically symmetric property)에 대해서 이해하고, 그것이 가져오는 문제와 해결책에 대해서 이해한다.
-
Filter Specification으로부터 Butterworth Filter, Chebyshev Filter를 이용하여 그 필터를 설계할 수 있다.
1. Frequency Transformation
가. Normalized Lowpass Filter
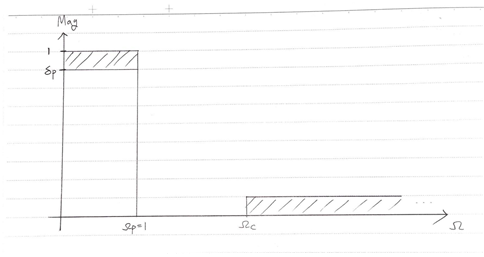
그림 1. Normalized Lowpass Filter의 형태
Normalized Lowpass Filter는 위의 그림과 같이 생겼다. Normalized Lowpass Filter(이하 NLPF)는 $\Omega_p=1$이라고 정해둔 일종의 Lowpass Filter이고, $\Omega_c$는 filter의 specification에 의해서 바꿀 수 있도록 변수로 설정되어있다. NLPF가 중요한 이유는 이 NLPF를 이용하여서 다른 어떤 형태의 필터로도 바꾸는 것이 가능하기 때문이다.
나. 이론의 설명에 앞선 용어 정리
설명의 편의를 위해, 다른 어떤 형태의 필터는 Other Kinds of Filters라고 하기 때문에, OKF라고 하겠으며, OKF는 모두 NLPF에서 Denormalized 된 형태이기도 하기 때문에, Denormalized Filters라고 할 수도 있음을 알려둔다.
그리고 다른 줄임말을 정리하자면, Lowpass Filter(LPF), Highpass Filter(HPF), Bandpass Filter(BPS), Bandstop Filter(BSP)라고 줄이도록 하겠다.
또한 변형되기 전·후의 Laplace frequency $s=j\Omega$의 구분을 위해, NLPF의 s를 대문자 S로 적고, 변형 된 후의 s를 소문자 s로 적는다는 것을 밝혀둔다.
다. Frequency Transformation from NLPF to OKF
1) NLPF $\rightarrow$ Denormalized LFP
일반적으로 NLPF에서 DLPF로 변형하기 위한 transformation은 다음과 같다.
Definition 1. Transformation
Normalized Lowpass Filter $\rightarrow$ Denormalized Lowpass Filter
passband frequency $\Omega_p$를 가지는 Denormalized Lowpass Filter를 Normalized Lowpass Filter로부터 얻으려면 다음과 같은 변형(transformation)을 적용할 수 있다.
\[S\rightarrow \frac{s}{\Omega_p}\]노파심에 한번 정리하자면, $S$를 $s/\Omega_p$로 변형하라는 말은 곧 $S$ 대신에 $s/\Omega_p$를 대입하라는 말과 같은 말이다.
이 transformation은 어렵지 않지만, frequency transformation의 타당성을 보여준다. 예를 들자면, transformation은 다음과 같은 과정을 통해서 이루어진다. 가령 다음과 같이 단순한 NLPF가 있다고 생각하자.
\[\frac{1}{S+1}\]이 LPF는 위의 NLPF DLPF의 transformation을 통해서 다음과 같이 변형될 수 있다.
\[\frac{1}{S+1}\rightarrow \frac{1}{s/\Omega_p +1}=\frac{\Omega_p}{s+\Omega_p}\]2) NLPF $\rightarrow$ Denormalized HPF
일반적으로, NLPF에서 DLPF로 변형하기 위한 transformation은 다음과 같다.
Definition2. Transformation
Normalized Lowpass Filter $\rightarrow$ Denormalized Highpass Filter
passband frequency $\Omega_p$를 가지는 Denormalized Highpass Filter를 Normalized Lowpass Filter로부터 얻으려면 다음과 같은 변형(transformation)을 적용할 수 있다.
\[S\rightarrow \frac{\Omega_p}{s}\]이 transformation이 타당한지 몇 개의 함수값을 통해서 검토해보도록 하자.
\[S = 0 \rightarrow s = \infty\] \[S = \infty \rightarrow s = 0\] \[S = \pm j \rightarrow s \mp j\Omega_p\]$S=\pm j$는 NLPF의 passband frequency를 가리킨다. 그것은 $s=j\Omega$의 관계 때문이다. 즉, $\Omega$-axis의 $\Omega_p$는 $s$-domain에서의 $j\Omega_p$를 가리키기 때문이다.
위의 검토를 통해서, Definition 2의 transformation은 NLPF에서 DHPF로의 변형이 알맞게 된다는 것을 확인할 수 있다. 이것 역시 간단한 예를 들어서 보여주자면, 다음과 같다.
\[\frac{1}{S+1}\rightarrow \frac{1}{\Omega_p/s + 1}=\frac{s}{\Omega_p+s}\]더불어, 또 생각해볼 것이, negative frequency의 존재이다.
\[S = \pm j \rightarrow s \mp j\Omega_p\]의 관계에서 볼 때, $S=j$에 해당하는 DHPF의 주파수는 $-j\Omega_p$이고, $S=-j$에 해당하는 DHPF의 주파수는 $j\Omega_p$임을 알 수 있다. 사실 수학적으로, 모든 filter에는 negative 주파수영역이 존재하고, 그것들의 amplitude는 y축을 중심으로 뒤집힌 모양을 하고 있다.
하지만, 우리는 0~$\infty$ 사이의 주파수에 관심이 있고, $S=-j$에 대응되어 양의 주파수$s=\Omega_p$가 출력되기 때문에 이 transformation은 수학적으로도 실용적으로도 문제가 없다. 우리는 필요한 결과만 얻어내면 그것으로 충분하기 때문이다.
3) NLPF $\rightarrow$ Denormalized BPF
일반적으로 NLPF에서 DBPF로 변형하기 위한 transformation은 다음과 같다.
Definition3. Transformation
Normalized Lowpass Filter $\rightarrow$ Denormalized Bandpass Filter
center frequency $\Omega_0$과 passband edge $\Omega_{p1}$과 $\Omega_{p2}$ ($\Omega_{p1}>\Omega_{p2}$)를 가지는 Denormalized Bandpass Filter를 Normalized Lowpass Filter로부터 얻으려면 다음과 같은 변형(transformation)을 적용할 수 있다.
\[S\rightarrow \frac{Q(s^2+\Omega_0^2)}{\Omega_0\times s}\]where $Q$ and $B$ are defined as
\[Q = \frac{\Omega_0}{B}\]and
\[B = \Omega_{p2}-\Omega_{p1}\]위 NLPF $\rightarrow$ DLPF, NLPF $\rightarrow$ DHPF 의 변형과 마찬가지로, Def. 3의 변형(transformation)의 타당성을 몇 가지 s와 그 대응값을 통해서 살펴보자.
\[S = 0\rightarrow s \pm j\Omega_0\] \[S =\infty \rightarrow s = \begin{cases}0 \\ \infty\end{cases}\]즉, NLPF의 $S=0$이었을 때의 값이 DBPF의 center frequency의 값으로 옮겨지고, $S=\infty$의 값이 DBPF의 0과 $\infty$의 값으로 옮겨지게 된다.
NLPF의 $S=\infty$의 값은 0또는 neglibigle한 값을 가지고 있기 때문에 Def.3 의 transformation을 통해서 얻을 수 있는 bandpass filter의 모양은 다음과 같다.
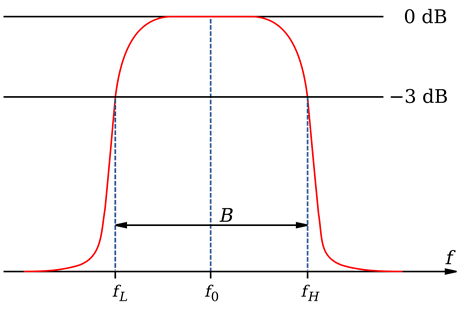
그림 2. Bandpass filter의 모양
이제, Banspass Filter가 가지는 passband Frequency에 대해서 생각해보도록 하자. 참고로 이 부분은 Bandpass filter를 구현하는 데에 있어서 가장 중요한 부분을 차지한다고 할 수 있다.
즉, $S=\pm j$일 때,
Derivation 1. Finding passband frequency in bandpass filter fron NLPF
proof)
① $S=+j$일 때,
Def. 3의 transformation 관계에 의해서,
\[\frac{Q(s^2+\Omega_0^2)}{\Omega_0 \times s} = j\] \[\Rightarrow s^2 +\Omega_0^2 -j\frac{Q_0\times s}{Q} = 0\] \[\Rightarrow s^2 - j\frac{\Omega_0}{Q}s+\Omega_0^2 = 0\]2차 방정식의 근의 공식에 의해서,
\[\therefore s = \frac{j\Omega_0/Q\pm\sqrt{-\Omega_0^2/Q^2-4\Omega_0^2}}{2}\] \[=\frac{j\Omega\pm\Omega_0\sqrt{-(1+4Q^2)}}{2Q}\] \[=\frac{j\Omega_0}{2Q}\left[1\pm\sqrt{1+4Q^2}\right]\]이 때, $\sqrt{1+4Q^2}>1$이라는 것은 명백하기 때문에, s의 한 근은 양수, 한 근은 음수라는 것을 알 수 있다.
② $s=-j$ 일 때,
마찬가지로, transformation의 식에 의해서,
\[\frac{Q(s^2 + \Omega_0^2)}{\Omega_0\times s} = -j\] \[s^2 + \Omega_0^2 + j\frac{\Omega_0\times s}{Q} = 0\] \[s^2 + j\frac{\Omega_0}{Q}s + \Omega_0^2 = 0\]2차 방정식의 1차 항의 계수만 부호가 바뀌었다는 것을 알 수 있다. 그렇기 때문에 간단하게, algebra를 생략하고 s를 바로 적을 수 있다.
\[s = j\frac{\Omega_0}{2Q}\left[-1\pm\sqrt{1+4Q^2}\right]\]즉, $s=-j$일 때에도 한 근은 양수이고 다른 한 근은 음수인 두 개의 근이 나온다.
③ 중간 결론
결론적으로, NLPF의 $\Omega_p=1$(or$S=\pm j$)에 의해서 DBPF는 네 개의 근이 발생한다는 것을 알 수 있다. 그리고 그 네 개의 근은 두 개의 양의 근과 두 개의 음의 근으로 구성되어 있다.
④ 근 사이의 관계(Relation between solutions) 이 때, 두 양의 근을 생각하면 다음과 같다. (우리는 양의 frequency만 생각해도 괜찮기 때문이다.)
\[s = j\frac{\Omega_0}{2Q}\left[\pm1+\sqrt{1+4Q^2}\right]\]즉, 다음과 같은 관계를 구할 수 있다.
\[S = j \rightarrow s = \pm j\Omega_{p1, p2}\] \[\Omega_{p1} = \frac{\Omega_0}{2Q}\left[\sqrt{1+4Q^2}-1\right]\] \[\Omega_{p2} = \frac{\Omega_0}{2Q}\left[\sqrt{1+4Q^2}+1\right]\]이 때, $\Omega_{p1}\times\Omega_{p2}=\Omega_0^2$라는 사실을 알 수 있다.
위 Derivation을 통해서 알 수 있었던 사실은 $\Omega_{p1}\times\Omega_{p2}=\Omega_0^2$이라는 사실이며, 이 사실은 Bandpass filter의 Center frequency를 정하거나, 역으로 Center Frequency를 통해서 Passband Edges를 구할 때 있어서 매우 중요한 사실이다.
다시 한번 정리하자면, center frequency는 두 passband edges의 산술평균이 아닌 기하평균이다.
또한, 이 기하평균은 passband edges 만이 아니라 어떠한 대칭되는 두 frequency에 대해서도 성립한다. 그러므로, stopband edges $\Omega_{s1}$과 $\Omega_{s2}$에 대해서도 성립한다. 따라서,
\[\Omega_0^2 = \Omega_{p1}\Omega_{p2}\] \[\Omega_0^2 = \Omega_{s1}\Omega_{s2}\]이고, passband edges와 stopband edges는 반드시 다음과 같은 관계가 성립되는 것들이어야 한다.
\[\Omega_0^2 = \Omega_{p1}\Omega_{p2} = \Omega_{s1}\Omega_{s2}\]그렇기 때문에, Butterworth filter를 설계할 때와 마찬가지로 $\Omega_p$와 $\Omega_s$를 모두 만족시키는 N을 구할 수 없듯이, consumer 가 요구하는 filter의 spec을 모두 만족시킬 수 있는 Bandpass filter는 존재하지 않을 수 있다.
그렇기 때문에, $\Omega_p$에 대해서는 exactly satisfy하면서 $\Omega_s$에 대해서는 over satisfy하는 bandpass filter를 설계할 수 밖에 없다.
4) NLPF $\rightarrow$ Denormalized BSF
이번엔 Bandstop filter를 설계해보자.
Definition 4. Transformation
Normalized Lowpass Filter $\rightarrow$ Denormalized Bandpass Filter
center frequency $\Omega_0$과 passband edge $\Omega_{p1}$과 $\Omega_{p2}$ ($\Omega_{p1}>\Omega_{p2}$)를 가지는 Denormalized Bandstop Filter를 Normalized Lowpass Filter로부터 얻으려면 다음과 같은 변형(transformation)을 적용할 수 있다.
\[S\rightarrow \frac{\Omega_0\times s}{Q(s^2+\Omega_0^2)}\]where $Q$ and $B$ are defined as
\[Q = \frac{\Omega_0}{B}\]and
\[B = \Omega_{p2}-\Omega_{p1}\]Bandstop Filter는 Bandpass Filter의 역수를 취한 값을 대입했다고 볼 수 있다. 위의 과정에서와 마찬가지로 몇 가지 값을 가지고 transformation의 타당성을 검증해보자.
\[S = 0 \rightarrow s = 0 \text{ or } \infty\] \[S = \infty \rightarrow s = \pm j\Omega_0\]그러므로, 다음과 같은 모양의 결과가 나온다는 것을 수식을 통해서 알 수 있다.
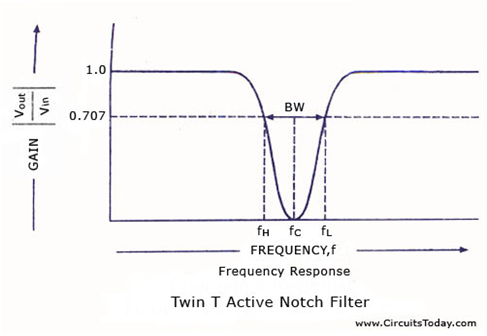
BPF에서와 마찬가지로 BSF에서도 기하평균 property가 적용된다. 즉,
\[\Omega_0^2 = \Omega_{p1}\Omega_{p2}=\Omega_{s1}\Omega_{s2}\]이다.
2. Practical problems that arise in making BPF or BSF
우리는 지금까지 LPF외에 다른 종류의 필터를 설계 할 때에는 Normalized LPF를 통해서 설계가 가능하다는 사실을 공부했다. 그 방법은 Frequency Transformation이라는 방법이고 구체적인 내용은 다음과 같았다.
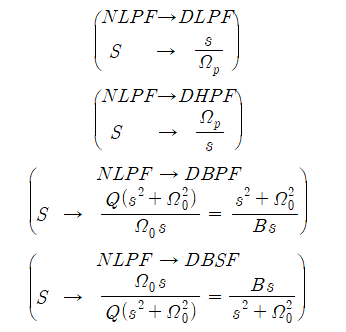
여기서 Bandpass Filter와 Bandstop Filter는
\[\Omega_0^2 = \Omega_{p1}\Omega_{p2} = \Omega_{s1}\Omega_{s2}\]을 만족해야한다. 이 관계는 $S=\pm j$일 때의 값을 찾는 2차 방정식의 해를 푸는 것과 관련이 있었다.
이 때, Filter의 설계를 요구 받을 때에는 대부분 $\Omega_0$는 주어지지 않고, $\Omega_{p1},\Omega_{p2}$와 $\Omega_{s1},\Omega_{s2}$가 주어진다.
이 때, 식(38)을 만족시킬 수 없는 $\Omega_{p1},\Omega_{p2}$와 $\Omega_{s1},\Omega_{s2}$라면 $\Omega_{s1}$ or $\Omega_{s2}$를 조절하여 stopband frequency에 대해서는 oversatisfying 하는 정상적인 (식 (38)을 만족시키는) Bandpass Filter 또는 Bandstop Filter를 구할 수 있다.
가. $\Omega_{s1}\Omega_{s2}>\Omega_{p1}\Omega_{p2}$, $\Omega_{p1}\Omega_{p2}=\Omega_0^2$인 경우
이 때, 우리는 $\Omega_{s1}\Omega_{s2}$의 크기를 줄여주는 작업을 해주어야 한다.
그렇다면, $\Omega_{s1}$과 $\Omega_{s2}$중에서 어떤 것을 작게 만들어야 할까? 아래의 그림을 보면서 생각해보자.
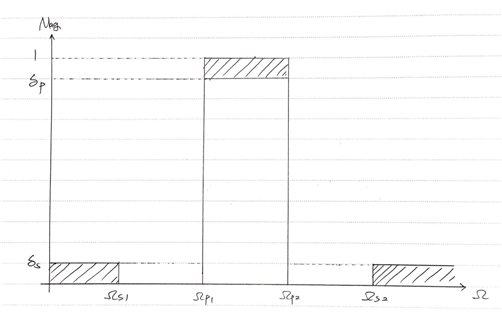
다시 한번 말하자면, 우리는 $\Omega_{s1}\Omega_{s2}>\Omega_{p1}\Omega_{p2}$, $\Omega_{p1}\Omega_{p2}=\Omega_0^2$인 경우에 처해있다.
이 때, Filter의 Specification을 oversatisfying 하기 위해서는 $\Omega_{s2}$를 줄여주어야 한다.
왜냐면, $\Omega_{s1}$을 작게 만들어주게 된다면 그것은 filter의 specification을 만족시켜주지 못하는 필터가 되기 때문이다.
그러므로, 새로 만들어지는 $\hat{\Omega}_{s2}$는 다음과 같이 될 것이다.
\[\hat{\Omega}_{s2}=\frac{\Omega_0^2}{\Omega_{s1}}\]나. $\Omega_{s1}\Omega_{s2}<\Omega_{p1}\Omega_{p2}$, $\Omega_{p1}\Omega_{p2}=\Omega_0^2$인 경우
이 경우는 $\Omega_{s1}\Omega_{s2}$의 크기를 키워주는 작업을 해야한다.
이 때 Filter의 Specification을 oversatisfying 하기 위해서는 $\Omega_{s1}$의 크기를 키워주어야 한다. 마찬가지로 새로 만들어지는 $\hat{\Omega}_{s1}$은 다음과 같을 것이다.
\[\hat{\Omega}_{s1}=\frac{\Omega_0^2}{\Omega_{s2}}\]다. Modifying $\Omega_s$ in NLPF
이제 Bandpass Filter의 Stopband edges를 조절했다면, 문제는 해당되는 NLPF의 Spec에는 어떤 영향을 미치는지 생각해보는 것이다. 우리는 $\delta_p$와 $\delta_s$가 주어져 있고, $\Omega_p$에 대한 정보도 충분하기 때문에, 그것들을 이용해서 NLPF에서의 $\Omega_s$에 대해서도 생각해볼 수 있다.
NLPF의 $\Omega_s$는 BPF로의 Transformation에 의해서 결정될 수 있다. 그것은,
\[S = \frac{s^2 +\Omega_0^2}{B\times s}\]와 같은 관계였다.
이 때, NLPF의 $\Omega_s$는, $S=j\Omega_s$와 같은 관계에 의해서 찾을 수 있다. 그리고, BPF의 stopband edges $\Omega_{s1,s2}$는 $s=j\Omega_{s1,s2}$와 같은 관계에 의해서 구할 수 있을 것이다.
그러므로, 다음의 식이 성립된다.
\[j\Omega_s = \frac{-\Omega_{s1}^2 + \Omega_0^2}{Bj\Omega_{s1}}\]또는
\[j\Omega_s = \frac{-\Omega_{s2}^2 + \Omega_0^2}{Bj\Omega_{s2}}\]따라서 여기서
\[\Omega_s = \frac{\Omega_0^2-\Omega_{s1}^2}{B\Omega_{s1}}\]또는
\[\Omega_s = \frac{\Omega_0^2-\Omega_{s2}^2}{B\Omega_{s2}}\]라는 것을 알 수 있다. 하지만 이 두 식에는 negative frequency를 말하고 있다는 것을 알 수 있다. 우리는 이 때, 조금 직관적인 방법을 통해서 positive frequency와 negative frequency는 그 부호만 반대일 뿐, 그 크기는 같은 값인 frequency라는 것을 알고 있다.
그렇기 때문에, 식 (44) 혹은 식 (45)와 같이 써도 무방하다. 다시 한번 상기시키자면, $\pm\Omega_s$에는 $\pm\Omega_{s1}$과 $\pm\Omega_{s2}$의 총 4개의 frequency가 mapping 된다. 그렇기 때문에 위와 같은 방법으로 양의 frequency를 찾는 것은 수학적으로 오류가 없다고 할 수 있다.
그러므로, $\Omega_{s1}$과 $\Omega_{s2}$중 $\Omega_{s1}$만 생각해보자면,
\[\Omega_{s(NLPF)}=\frac{\Omega_0^2-\Omega_{s1}^2}{B\Omega_{s1}}\] \[=\frac{\Omega_0^2}{B\Omega_{s1}}-\frac{\Omega_{s1}^2}{B\Omega_{s1}}\] \[=\frac{\Omega_{s1}\Omega_{s2}}{B\Omega_{s1}}-\frac{\Omega_{s1}^2}{B\Omega_{s1}}\] \[=\frac{\Omega_{s2}-\Omega_{s1}}{B}\] \[=\frac{\Omega_{s2}-\Omega_{s1}}{\Omega_{p2}-\Omega_{p1}}\]이다.
3. 필터를 설계하는 순서
① Other Kind of Filter (NLPF 외의 필터)의 스펙을 받는다.
② 그 스펙을 NLPF의 스펙으로 변환시킨다. (Transformation이나 2-다.에서 구한 방식으로 $\Omega_s$를 찾는다.)
③ NLPF를 디자인한다.
④ Transformation $S=f(s)$를 사용하여 필터를 변환시킨다.
⑤ OKF의 $H_{OKF}(s)$를 구할 수 있다.