상관 계수의 용도와 정의

상관 계수는 연속적으로 변하는 두 변수 간의 (상관) 관계를 확인하고 싶을 때 사용할 수 있다.

가령 몸무게와 키의 상관 관계라던지, 수학 점수와 영어 점수 간의 상관관계 같은 것들을 확인할 수 있다.

연속적으로 변하는 두 변수 간의 관계는 시각적으로도 확인할 수도 있는데 두 개의 연속적으로 변하는 n개의 변수 쌍을 각각 x 축과 y 축에 대입해서 그리면 산점도(scatter plot)를 그릴 수 있다.

예를 들어 아래는 500명 학생의 수학, 영어 점수의 산점도를 그린 것이다.

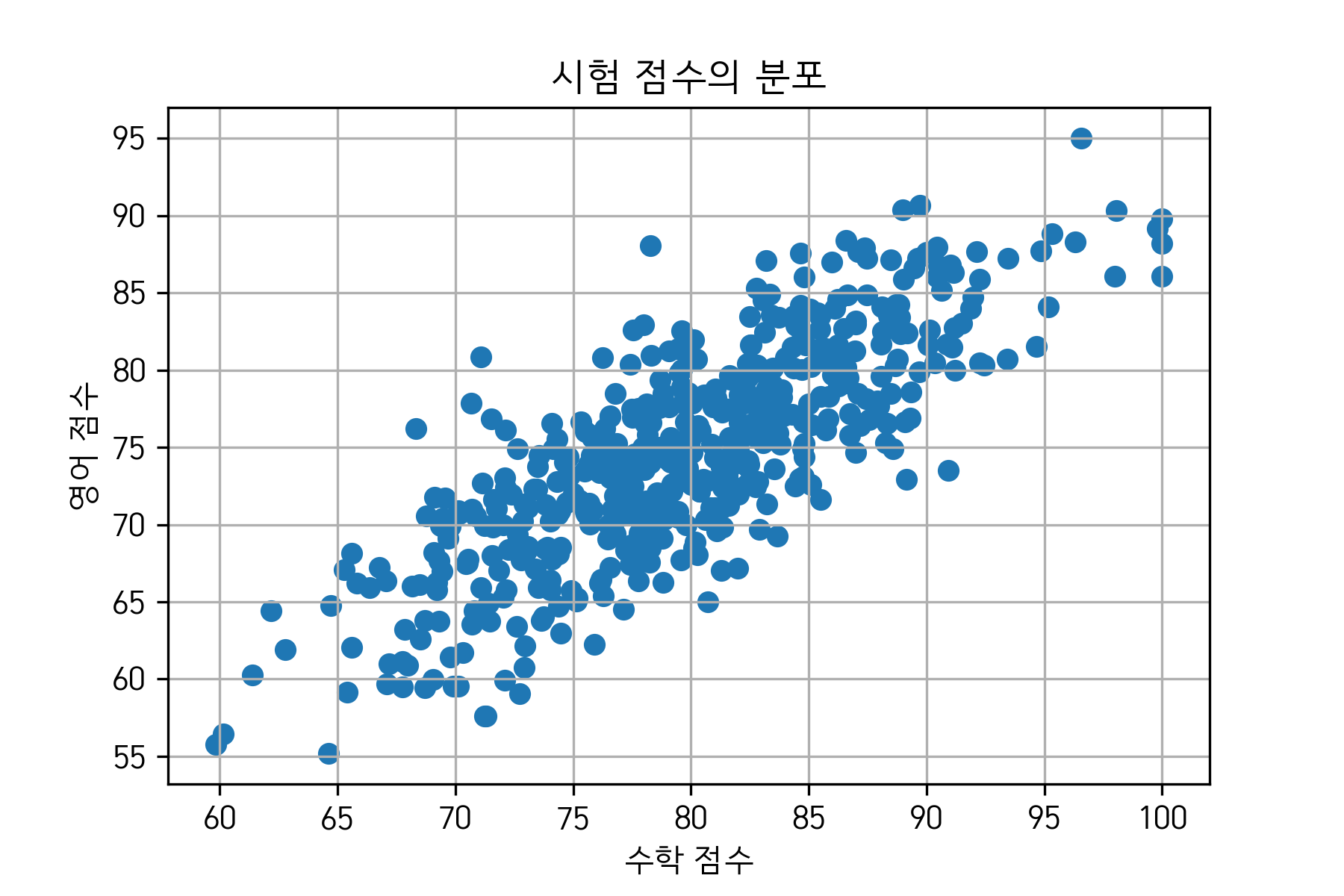
그림 1. 산점도의 예시 plot. 수학 점수와 영어 점수 간의 양의 상관 관계가 보인다.

상관 계수는 다음과 같이 정의할 수 있다.

n개의 dataset 에 대해서

\[r = \frac{1}{n-1}\sum_{i=1}^{n} \left(\frac{x_i-\bar{X}}{s_{\bar{X}}}\right) \left(\frac{y_i-\bar{Y}}{s_{\bar{Y}}}\right)\]

그림 1에서와 같이 500명의 데이터에 대해 상관 관계를 확인하라고 하면

이 식에 대입해서 숫자를 출력하면 되지만 이 식은 과연 어떤 의미가 있는 것일까?

그것은 벡터의 내적과 관련되어 있다.

벡터의 내적

임의의 2차원 벡터 $\vec{a}$, $\vec{b}$를 생각해보자.

두 벡터의 내적은 다음과 같이 정의된다.

\[\vec{a}\cdot\vec{b} = \sum_{i=1}^{n}a_ib_i\]

가령, 벡터 $\vec{a}$, $\vec{b}$를 각각 (2,3), (3,0)이라고 한다면 두 벡터의 내적은

\[\vec{a}\cdot\vec{b} = \sum_{i=1}^{n}a_ib_i = (2\times 3)+(3\times 0) =6\]

이다.

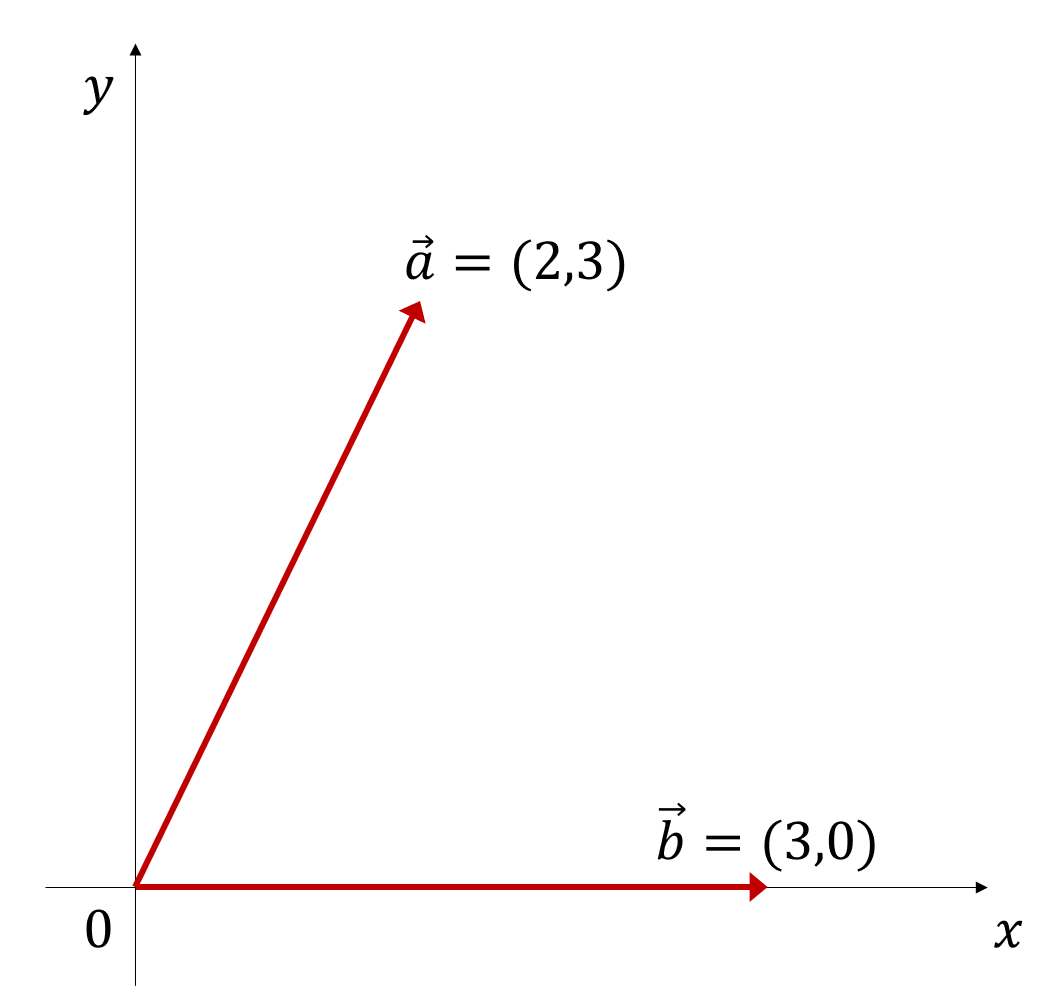
그림 2. a = (2,3), b= (3,0)의 두 벡터를 2차원 평면상에 도시한 것

한편, 벡터의 내적은 기하학적으로

’$\vec{a}$의 $\vec{b}$로의 정사영에 $\vec{b}$의 크기를 곱한 것’

이라는 의미도 가진다.

즉, 아래의 그림 3에서 볼 수 있듯이 기하학적 의미로 두 벡터의 내적은

\[\vec{a}\cdot\vec{b} = |\vec{a}|\cos(\theta)\times|\vec{b}|\]

이다.

"벡터 a의 변화를 벡터 b가 얼마만큼 설명해줄 수 있는가?”

라고 말이다.


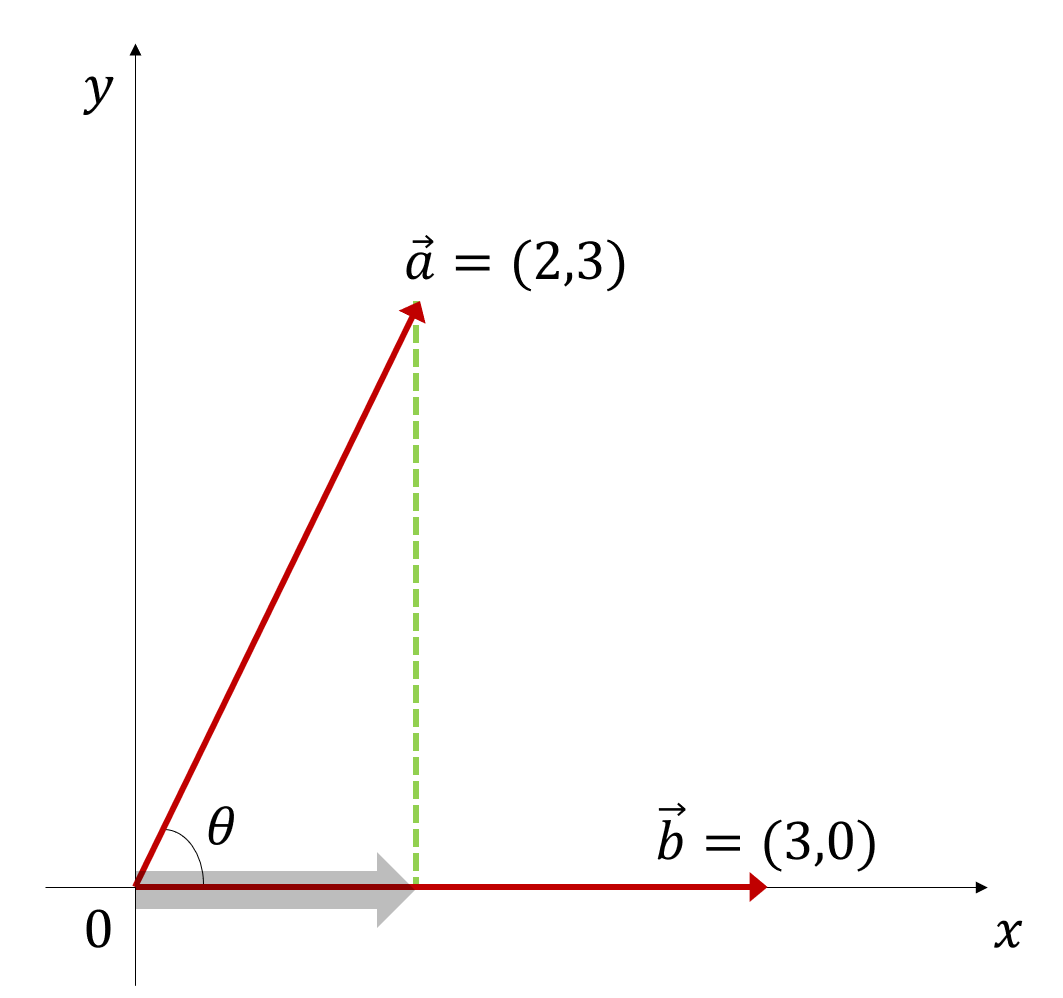
그림 3. 벡터 a에서 벡터 b로 향하는 정사영

그렇다면 두 벡터의 내적과 $\vec{b}$의 크기를 이용하면 $\vec{a}$의 $\vec{b}$로의 정사영의 길이를 알 수 있다.

즉, $\vec{a}$의 $\vec{b}$로의 정사영의 길이 $proj_b a$ 는 다음과 같다.

\[proj_ba = \frac{\vec{a}\cdot\vec{b}}{|\vec{b}|}\]

이 때 우리는 $proj_ba$의 의미를 조금 다르게 해석해 볼 수도 있다.

한편, $\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$이다.

즉, 내적의 순서는 상관없다. 다시 말하면 $\vec{b}$의 $\vec{a}$로의 정사영의 길이, $proj_ab$는 다음과 같이 구할 수 있다.

\[prok_ab = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}|}\]

마찬가지로 $proj_ab$ 또한 이렇게 해석해 볼 수 있겠다.

"$\vec{b}$의 변화를 $\vec{a}$가 얼마만큼 설명해줄 수 있는가?”


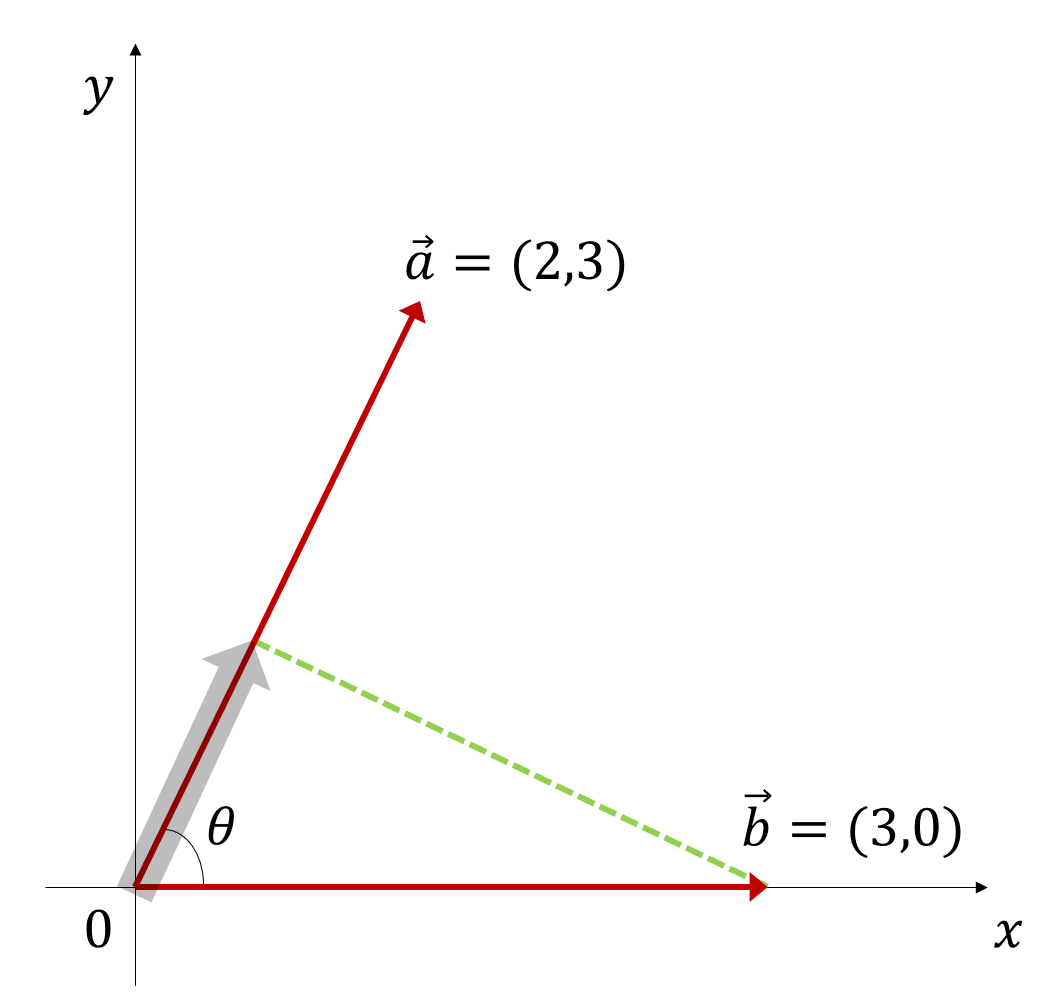
그림 4. 벡터 b에서 벡터 a로 향하는 정사영

종합하자면 다음과 같이 설명할 수 있을 것이다.

① $\vec{a}$와 $\vec{b}$의 관계를 알고싶다.

\[\Rightarrow \vec{a}\cdot\vec{b}\]

② $\vec{a}$가 $\vec{b}$를 설명하는 정도를 파악하려면?

\[\Rightarrow \times \frac{1}{|\vec{a}|}\]

③ $\vec{b}$가 $\vec{a}$를 설명하는 정도를 파악하려면?

\[\Rightarrow \times \frac{1}{|\vec{b}|}\]

따라서 $\vec{a}$와 $\vec{b}$가 서로를 설명하려면

\[\rightarrow \times \frac{1}{|\vec{a}|} \times \frac{1}{|\vec{b}|}\]

그러니까 $\vec{a}$와 $\vec{b}$가 서로를 설명하는 양은

\[\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|} = \cos(\theta)\]

라고 할 수 있다.

다시 상관 계수로 !

다시 상관 계수의 식을 보자.

\[r = \frac{1}{n-1}\sum_{i=1}^{n} \left(\frac{x_i-\bar{X}}{s_{\bar{X}}}\right) \left(\frac{y_i-\bar{Y}}{s_{\bar{Y}}}\right)\]

이 중에서

\[\frac{x_i-\bar{X}}{s_{\bar{X}}}\]

와

\[\frac{y_i-\bar{X}}{s_{\bar{Y}}}\]

는 정규화 과정과 매우 관련이 있어 보이긴 한다. 하지만 이번에는 $(x_i-\bar{X})$와 $(y_i-\bar{Y})$를 떼어서

생각해보자. 그리고 $s_{\bar{X}}$와 $s_{\bar{Y}}$는 본래의 정의를 이용해 $(x_i-\bar{X})$, $(y_i-\bar{Y})$를 이용해서 풀어서 써보도록 하자.

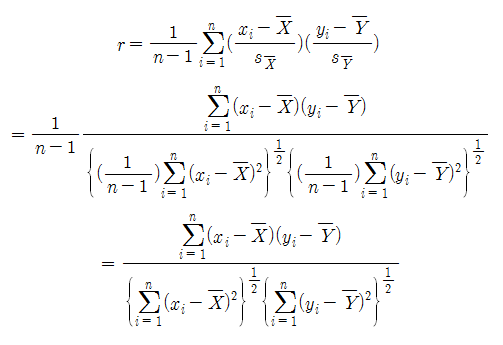
여기서 $a_i=x_i-\bar{X}$, $b_i=y_i-\bar{Y}$라 하자.

그러면 위 식은 다음과 같이 쓸 수 있다.

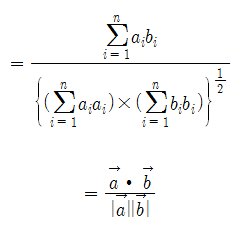
다시 말하면 상관 계수 $r$은

”$\vec{a}$와 $\vec{b}$의 관계에 대해 서로가 얼마나 서로를 설명하는가?”

또는

“$x_i-\bar{X}$와 $y_i-\bar{Y}$의 관계에 대해 서로가 얼마나 서로를 설명하는가?”

라는 뜻이 라고 해석할 수 있겠다. 이 말은 다시 말하자면 dataset이 원점으로부터 얼마나 떨어져있는지는 무시하고 서로 퍼진 정도만 보겠다는 의미이다.

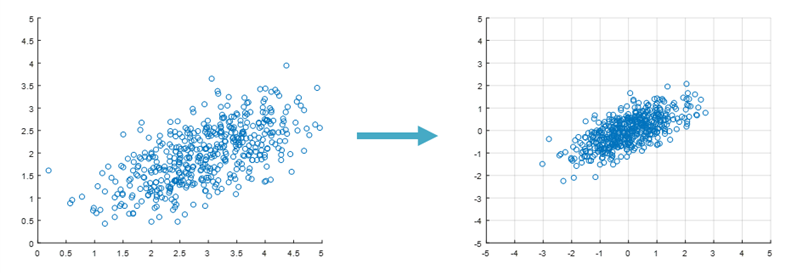
그림 5. 왼쪽 그림에서는 산점도의 중심이 (3,2)이지만 상관 관계는 데이터 셋이 원점으로부터 얼마나 떨어져있는지 관계없는 양이다. 따라서 오른쪽 그림처럼 상관 관계의 식으로부터 원점으로만큼 떨어진 정도를 무시할 수 있게 한다.

또 한편,

\[\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|} = \cos(\theta)\]

이었는데,

\[-1\leq\cos(\theta)\leq 1\]

이므로,

\[-1\leq r\leq 1\]

라고 말하는 것은 매우 자연스럽게 생각할 수 있다.

상관계수와 공분산의 차이에 대해서,

질문이 들어온 것을 다시 한번 글에서 설명하자면,

상관계수와 공분산 모두 공통적으로 벡터의 내적을 이용해 설명할 수 있고, 데이터 간의 (즉, 벡터 사이의) ‘닮음’과 연결 지을 수 있다.

다만, 둘 사이의 가장 두드러지는 차이점은 정규화의 방법인데, 상관계수는 벡터의 크기로 정규화해주는 반면 공분산은 벡터의 원소 수를 가지고 정규화해준다.