Prerequisites
아래의 내용에 대해 잘 알고 오는 것을 추천드립니다.
- 중심극한정리의 의미
- 추천 JS Applet: Seeing Theory
- 최대우도법(Maximum Likelihood Estimation)
- 관련 내용 추천 Youtube 비디오: StatQuest
- 위 영상 정리 blog: BetterThanWholwas
- 추천 JS Applet: Seeing Theory
- 경사하강법(Gradient Descent)
ICA 모델과 목적
위키피디아에 따르면 독립 성분 분석(Independent Component Analysis, ICA)은 다변량의 신호를 통계적으로 독립적인 하부 성분으로 분리하는 계산 방법이라고 되어 있다.
말이 어려워 보이지만, 아래의 예시를 보면서 ICA가 할 수 있는 일이 어떤 것인지 알아보도록 하자.
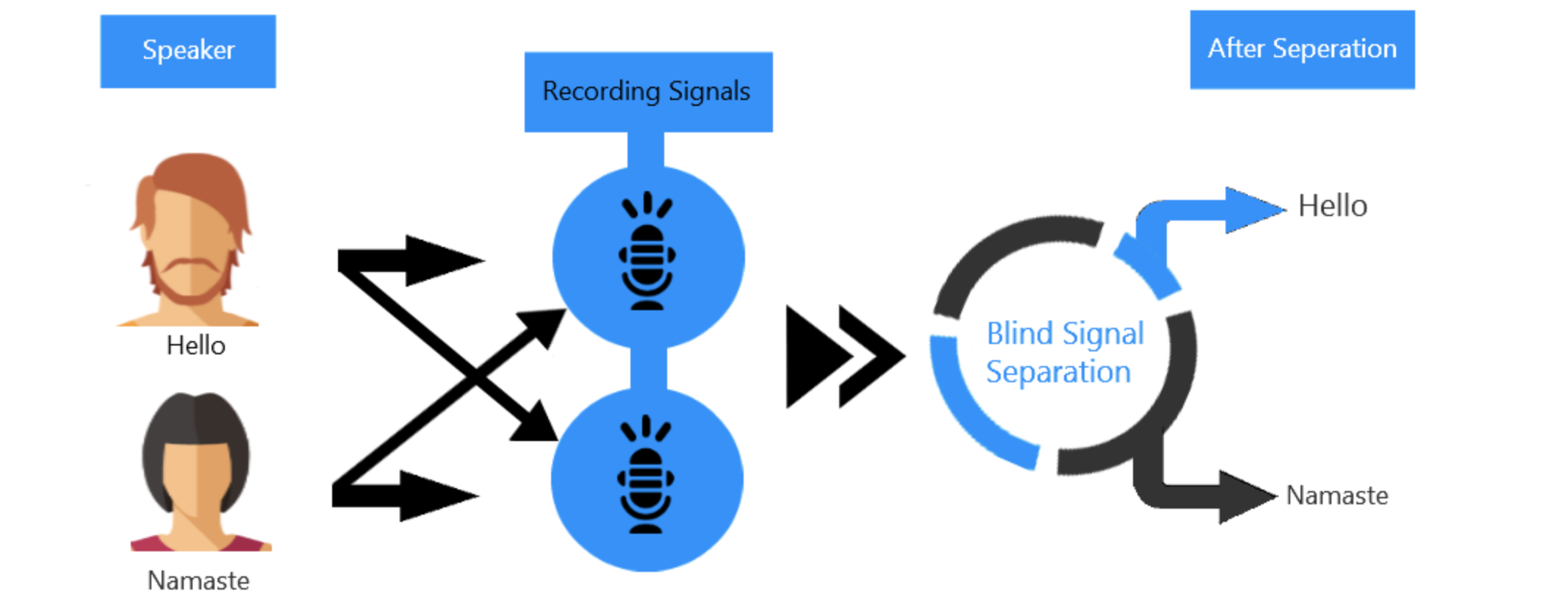
그림 1. ICA가 할 수 있는 일을 block diagram으로 나타낸 것.
섞여버린 두 개의 음원을 분리해내는 과정을 보여주고 있다.
(Blind Source Separation라고 적힌 것이 ICA가 하는 일)
출처: gowrishankar.info blog
방에서 두 사람이 동시에 말을 하고 있다고 생각해보자. 그리고 두 개의 마이크로 녹음을 진행하고 있다고 생각해보자.
두 개의 마이크로 녹음된 신호를 각각 $x_1(t), x_2(t)$라고 하고, 두 사람의 음성 신호를 각각 $s_1(t), s_2(t)$라고 하면,
이 식들의 관계를 다음과 같이 선형 방정식으로 표현할 수 있다.
\[x_1(t) = a_{11}s_1(t)+a_{12}s_2(t)\] \[x_2(t) = a_{21}s_1(t)+a_{22}s_2(t)\]여기서 $a_{ij}$ with $i,j = 1, 2$는 마이크로부터 발화자까지의 거리와 관련된 변수라고 하자.
우리가 원하는 것은 두 녹음 음원으로부터 원래의 음원을 분리해내는 일이다. 즉, $s_1(t)$와 $s_2(t)$를 복원해내는 일이다.
식 (1)과 식 (2)를 행렬로 표현하면 다음과 같다.
\[x = As\]여기서 $A$를 mixing matrix라고 부르도록 하자.
또, 여기서 $x\in \mathbb{R}^n$, $A\in\mathbb{R}^{n\times n}$, $s\in\mathbb{R}^n$이다.
만약에 우리가 $A$를 알 수만 있다면 $A^{-1}$을 양변의 왼쪽에 곱해서 쉽게 source $s$를 찾을 수 있다.
즉, 아래와 같은 방법으로 source를 찾을 수 있는 것이다.
\[s = A^{-1}x = Wx\]우리의 목적은 이 unmixing matrix $W = A^{-1}$ 행렬을 찾는 것이다. 하지만, $A$ 행렬을 모르는 상태에서 어떻게 $W$ 행렬을 찾을 수 있을까?
중심극한정리와 독립성분분석
독립 성분 분석(Independent Component Analysis, ICA)을 잘 이해하기 위해선 중심극한정리(Central Limit Theorem, CLT)에 대해 잘 알고 오는 것이 중요하다고 할 수 있다.
왜냐면 ICA의 개념은 CLT를 정 반대로 생각한 것이기 때문이다.
CLT를 짧게나마 복습해보면, 서로 독립적인 랜덤 변수들의 선형조합으로 이루어진 새로운 랜덤 변수의 분포는 가우스 분포를 따른다는 것이다.
특히 중요한 것은 선형 조합에 들어가는 독립 변수들이 많으면 많을 수록 더 가우스 분포에 가까워진다는 점이다.
CLT와 ICA를 각각 그림으로 표현하자면 아래와 같다.
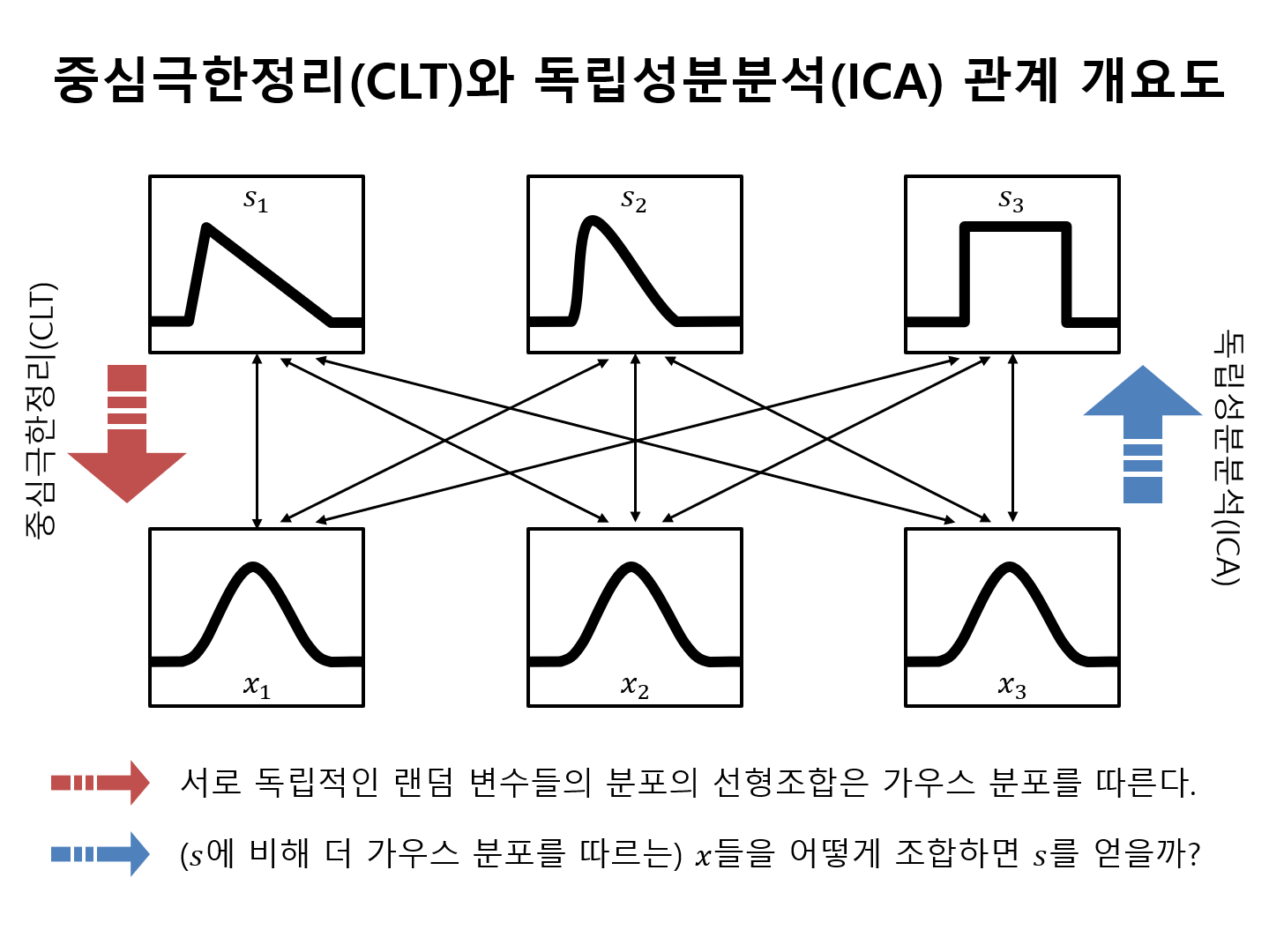
그림 2. 중심극한정리와 독립성분분석의 관계 개요도
즉, ICA를 중심극한정리의 반대 과정으로 생각해본다면 ICA는 독립 랜덤 변수들의 조합으로 얻어진 $x$에 적절한 행렬 $W = A^{-1}$을 곱해
원래의 독립 랜덤 변수들인 source들인 $s$를 찾는 과정이다.
다시 말해 ICA에서는 source들이 서로 독립적이라는 가정을 최대한 만족할 수 있도록하는 $W=A^{-1}$을 찾는 것 을 목적으로 한다고 생각할 수 있다.
Densities and linear transformation
독립성분분석에 대한 알고리즘을 이해하기 위해 필요한 마지막 개념으로써, 랜덤 변수에 선형변환을 적용했을 때 변환 적용 전 후 변수의 확률 밀도 간의 관계를 생각해보도록 하자.
확률밀도함수의 면적의 총 합은 1이 되어야 하므로 어떤 행렬로 랜덤 변수를 선형변환 해주면 그 확률밀도함수는 행렬식을 이용해 보정해주어야 한다.
예를 들어, 랜덤 변수 $s$를 $s\sim Uniform[0,1]$라고 하자. 다시 말해 $s$의 density function은 $p_s(s) = 1\lbrace s\leq 0 \leq 1\rbrace$ 이라고 할 수 있다.
여기서 1{조건}은 조건이 만족될 때 1 아닌 경우 0을 출력하는 함수이다.
이 때, $A = 2$라고 하고 $x = As$이고, $s = A^{-1}x = Wx$ 라고 할 때, $’p_x(x) = p_s(Wx)’$가 아니라 $p_x(x) = p_s(Wx)\cdot |W|$이다.
아래의 그림을 보면 좀 더 이해하기 쉬울 것이다.
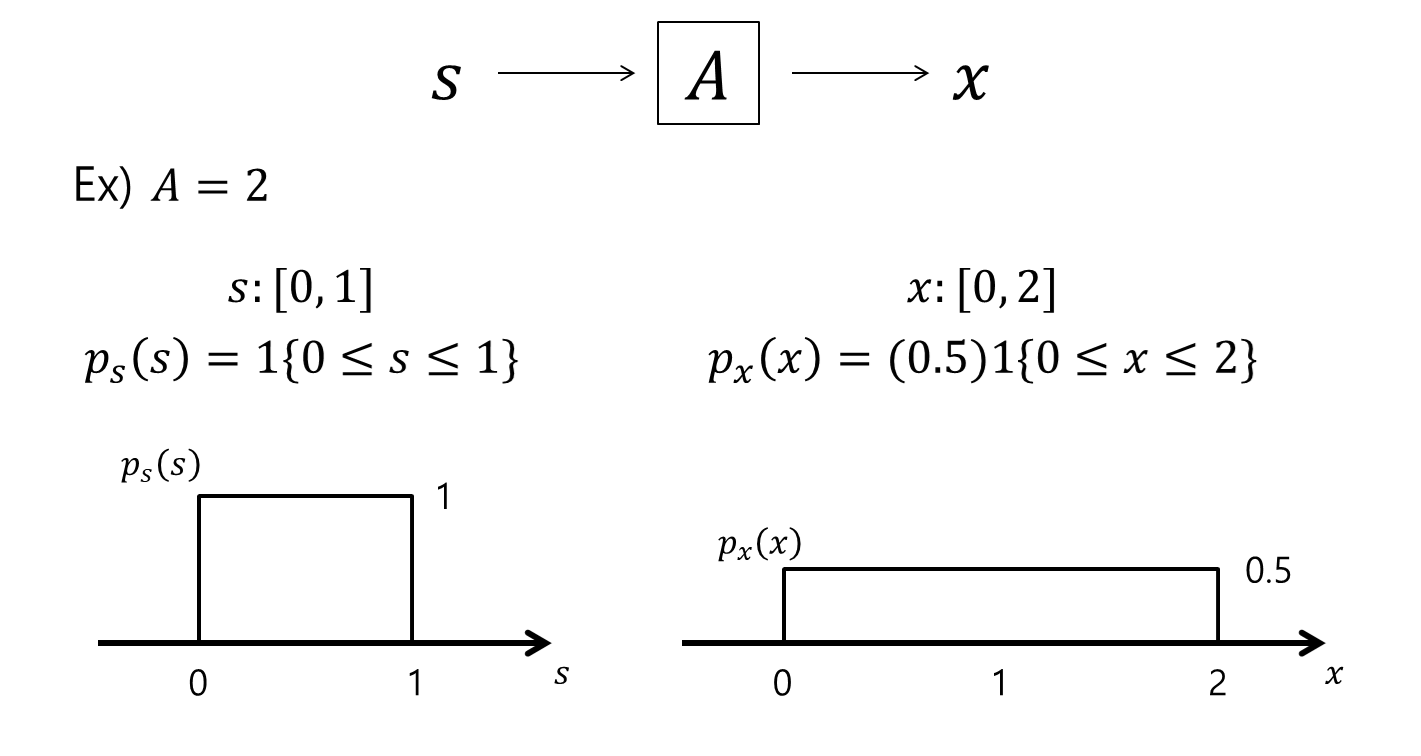
그림 3. 선형 변환 적용 전, 후의 랜덤변수의 확률밀도함수에 관한 예시.
따라서, $x=As$이고, $s=A^{-1}x=Wx$라는 점을 생각했을 때, 아래와 같이 선형 변환 후의 랜덤 변수의 확률밀도함수를 표시할 수 있다.
다시 쓰자면 아래와 같은 방식으로 $p_x(x)$를 구할 수 있다.
\[p_x(x) = p_s(A^{-1}x))\cdot|A^{-1}|\notag\] \[= p_s(s)\cdot|A^{-1}|=p_s(Wx)\cdot|W|\]ICA algorithm
Bell-Sejnowski algorithm
각 source $s_i$의 density function을 $p_s$라고 하면, 모든 source로 구성된 joint distribution은 다음과 같다.
\[p(s) = \prod_{i=1}^{n}p_s(s_i)\]바로 앞 꼭지에서 확인한 바와 같이 $x = As = W^{-1}s$라는 관계에서 $p(x)$를 구하면,
\[p(x) = \prod_{i=1}^{n}p_s(w_i^Tx)\cdot|W|\]이다. 굳이 $p(x)$를 계산하는 것은 우리가 실제로 확인할 수 있는 데이터는 $s$가 아니라 $x$이기 때문이다.
이제 우리가 획득하는 training samples $\lbrace x^{(i)}; i = 1, 2, \cdots, m \rbrace$의 density function $p(x)$에 대해서 log likelihood를 계산하도록 하자.
likelihood를 계산하는 이유는 수많은 parameter 중 어떤 parameter를 쓰는게 지금까지 얻은 정보들을 잘 설명할 수 있는지를
알아보기 위함이다. 일반적으로 계산의 편리함을 위해 likelihood 대신 자연로그를 붙인 log likelihood를 계산한다.
$m$개의 학습 데이터와 $n$개의 source에 대해 log likelihood를 계산하면 다음과 같다.
\[l(W) = \sum_{i=1}^{m}\left(\sum_{j=1}^{n}\log p_s(w_j^Tx^{(i)})+log|W|\right)\]여기서, $w_j^T$는 $W$ 행렬의 $j$ 번째 행이다.
\[W = \begin{bmatrix} { }- { } w_1^T { }- { } \\ { }- { } w_2^T { }- { } \\ \vdots \\ { }- { } w_n^T { }- { } \\ \end{bmatrix}\]또, 여기서 우리는 $p_s$에 대한 구체적인 확률밀도함수를 결정해볼 수 있다.
일반적으로 $p_s$의 CDF로 $g(s) = 1/(1+e^{-s})$ (즉, sigmoid 함수)를 사용했을 때 알고리즘의 사용에 문제가 없다고 알려져 있다.
(만약 source의 density에 대한 사전지식이 있다면 해당 density function을 사용하면 된다.)
따라서, pdf인 $p_s$는 $g’(s)$이므로, 위 $l(W)$는 다음과 같이 쓸 수 있다.
\[l(W) = \sum_{i=m}^{m}\left(\sum_{j=1}^{n}\log g'(w_j^Tx^{(i)})+log{|}W{|}\right)\]이제, $\nabla_W|W|=|W| (W^{-1})^T$ 라는 사실을 이용하여 $l(W)$를 $W$에 대해 편미분 해보자.
이 때, 수식 작성의 편의를 위해 $w_j^Tx^{(i)}$를 $s_j$로 치환해서 쓰도록 하자.
\[\frac{\partial l}{\partial W} = \sum_{i=1}^{m}\left(\sum_{j=1}^{n}\frac{1}{g'(s_j)}\cdot g''(s_j)\cdot x^{(i)^T} + \frac{1}{|W|}|W|(W^{-1})^T\right)\] \[= \sum_{i=1}^{m}\left(\sum_{j=1}^{n}\frac{1}{g(s_j)(1-g(s_j))}\cdot g(s_j)(1-g(s_j))(1-2g(s_j))\cdot x^{(i)^T} + (W^{-1})^T\right)\] \[= \sum_{i=1}^{m}\left(\sum_{j=1}^{n}(1-2g(s_j))\cdot x^{(i)^T} + (W^{-1})^T\right)\]Gradient Ascent 방법을 이용하면 $W$는 아래와 같이 update 할 수 있다.
\[W := W + \alpha \frac{\partial l}{\partial W}\]따라서, 각 $j = 1, 2, \cdots, n$에 대해,
\[W := W + \alpha\left(\begin{bmatrix} 1 - 2g(w_1^Tx^{(i)}) \\ 1 - 2g(w_2^Tx^{(i)}) \\ \vdots \\ 1 - 2g(w_n^Tx^{(i)}) \end{bmatrix} x^{(i)^T} + (W^T)^{-1}\right)\]여기서 $\alpha$는 learning rate이다.
위의 알고리즘이 수렴한 뒤에 얻은 $W$를 이용하면 원래의 sources, $s$를 얻을 수 있게 된다.
natural gradient algorithm
위에서 계산한 Bell-Sejnowski algorithm은 $W$를 업데이트 할 때 마다 계산해줘야하는 역행렬 term $(W^T)^{-1}$이 있어 계산 속도가 느리다는 단점이 있다.
이를 보완하기 위해 만들어진 것이 natural gradient algorithm인데 그 유도 과정은 그렇게 어렵진 않다.
식 (15)에서 $\alpha$ 오른쪽의 괄호 안에 있는 term의 우측에 $W^TW$를 곱하면 다음과 같다.
\[\left(\begin{bmatrix} 1 - 2g(w_1^Tx^{(i)}) \\ 1 - 2g(w_2^Tx^{(i)}) \\ \vdots \\ 1 - 2g(w_n^Tx^{(i)}) \end{bmatrix} x^{(i)^T} + (W^T)^{-1}\right)W^TW\] \[=\left(\begin{bmatrix} 1 - 2g(w_1^Tx^{(i)}) \\ 1 - 2g(w_2^Tx^{(i)}) \\ \vdots \\ 1 - 2g(w_n^Tx^{(i)}) \end{bmatrix} x^{(i)^T}W^TW + (W^T)^{-1}W^TW\right)\] \[=\left(\begin{bmatrix} 1 - 2g(w_1^Tx^{(i)}) \\ 1 - 2g(w_2^Tx^{(i)}) \\ \vdots \\ 1 - 2g(w_n^Tx^{(i)}) \end{bmatrix} x^{(i)^T}W^T + I\right)W\]따라서 식 (18)로부터 얻은 값을 이용해 weight를 업데이트하게 되면 역행렬 계산을 수행하지 않고도 조금 더 빠르게 gradient ascent 계산이 가능하다.
\[W := W + \alpha \frac{\partial l}{\partial W}W^TW\]즉, 아래의 과정을 통해 W를 업데이트 할 수 있다.
\[W := W + \alpha\left( \begin{bmatrix} 1 - 2g(w_1^Tx^{(i)}) \\ 1 - 2g(w_2^Tx^{(i)}) \\ \vdots \\ 1 - 2g(w_n^Tx^{(i)}) \end{bmatrix} x^{{(i)^T}}W^T + I \right)W\]PCA와 ICA의 차이
※ PCA에 대해 잘 모르는 경우 –> 여기 클릭
PCA와 ICA 모두 공통적으로 주어진 데이터를 대표하는 기저벡터를 찾아준다는 점에서는 같은 역할을 한다고 할 수 있다.
PCA는 feature space에서 직교하는 기저 벡터 집합을 찾아준다.
특히, PCA는 데이터를 정사영했을 때 maximum variance를 얻을 수 있는 벡터를 차례대로 기저벡터로 삼는 특징이 있다.
반면 ICA를 통해 찾은 기저벡터들은 서로 직교하지 않을 수도 있다.
ICA는 ICA를 통해 얻은 기저벡터들에 데이터를 정사영했을 때 그 결과들이 최대한 독립적(non-Gaussian)일 수 있도록하는 벡터들을 기저벡터로 삼는 특징이 있다.
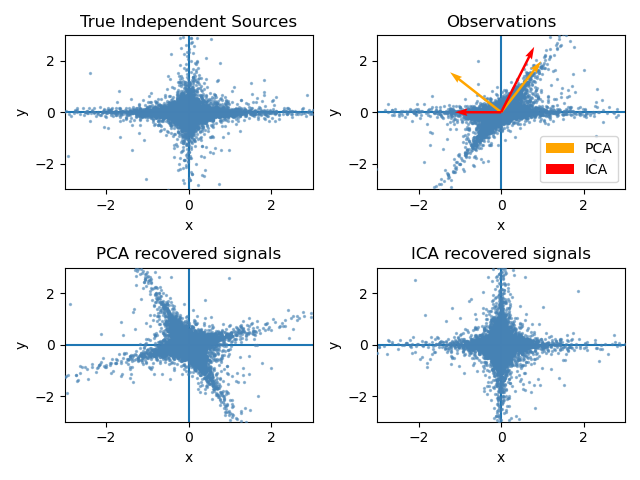
그림 4. PCA와 ICA의 비교
참고 문헌
- Independent Component Analysis / CS229 Lecture Notes / Andrew Ng
- Independent Component Analysis 1: Definition / Aapo Hyvarinen
- Independent Component Analysis 2: Estimation by maximization of non-Gaussianity / Aapo Hyvarinen
- Independent Component Analysis 3: Maximum Likelihood Estimation / Aapo Hyvarinen