Prerequisites
이 포스트를 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것을 추천드립니다.
아래의 EM 알고리즘까지 충분히 더 이해하시려면 이 내용도 알고오시는 것이 좋습니다.
여기서 나이브 베이즈 분류기에 대해서는 Prior의 의미에 대해 집중적으로 이해하는 것을 추천합니다.
GMM (Gaussian Mixture Model)
[복습] 최대우도법을 이용한 정규분포 fitting
이전 최대우도법 시간에서는 어떤 데이터를 관찰하고 그 데이터에 맞는 모수를 추정하는 방법을 알아보았다.
특히, 예시로써 확인해 본 것은 주어진 데이터에 대한 정규분포의 fitting 이었다.
아래의 그림 1에서는 최대우도법을 이용하여 여러 평균값의 후보 중 적절한 것을 선택하는 예시를 보여주고 있다.
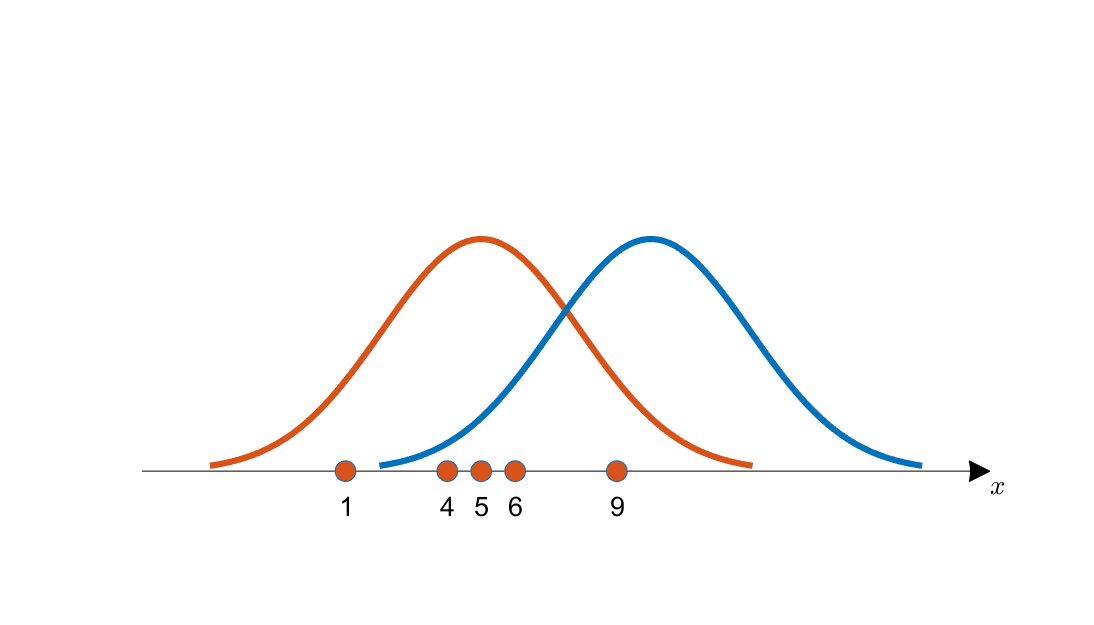
그림 1. 획득한 데이터와 추정되는 후보 분포 2개(각각 주황색, 파란색 곡선으로 표시)
좀 더 자세한 내용은 최대우도법 포스팅을 보는것이 좋겠으나 그림 1의 내용만을 간단히 얘기하자면, 수직선 상에 표시된 주황색 데이터들은 그림 1의 주황색 커브와 파란색 커브 중 주황색 커브로 부터 나왔을 가능성이 더 커보인다. 이것이 최대우도법의 핵심이었다.
그리고, 데이터에 대해 정규분포를 가정했을 때, 주어진 $m$개의 데이터에 대한 두 파라미터(평균, 분산)에 대한 최대우도법의 결론은 다음과 같았다.
우리에게 주어진 데이터를 $\lbrace x^{(1)}, x^{(2)}, \cdots, x^{(m)}\rbrace$이라 했을 때 평균, 분산 값을 계산할 때 likelihood 함수가 최대가 된다.
\[\hat{\mu}= \frac{1}{m}\sum_{i=1}^{m}x^{(i)}\] \[\hat{\sigma}^2= \frac{1}{m}\sum_{i=1}^{m}(x^{(i)}-\mu)^2\]위 결과는 우리가 익히 알고있는 평균, 분산에 관한 식이다. 하지만 이 결과는 주어진 데이터에 대한 우도(likelihood)를 계산한 뒤, 우도가 최대가 되게하는 평균과 분산 값을 얻은 결과라는 점을 기억해두도록 하자.
우리가 처한 문제와 해결 방법
※※※※※ 주의 ※※※※※
이 꼭지에서 설명하는 해결방법은 GMM 알고리즘을 완전히 설명한 것이라고 볼수는 없다.
왜냐면 아래의 EM 알고리즘 꼭지에서 설명할 $\phi$(즉, prior)에 대해 고려하지 않은 채 likelihood 관점에서만 GMM 알고리즘을 부분적으로 설명하고 있기 때문이다.
하지만, GMM 알고리즘의 진행에 관한 큰 구도를 이해함으로써 EM 알고리즘의 이해를 돕는 것에 이 꼭지에 목적이 있음을 주의하고 글을 읽어주길 바란다.
그럼에도 GMM 알고리즘의 구체적인 작동 방식에 큰 관심이 없는 독자라면 이 꼭지의 글만으로도 충분할 것으로 생각된다.
아래의 그림 2에서와 같이 수직선 상에 데이터가 10개 주어져 있다고 생각해보자.
여기서 우리에게는 각 데이터에 label이 주어져있다고 해보자. (동그라미 안의 색깔이 서로 다른 label을 의미한다.)
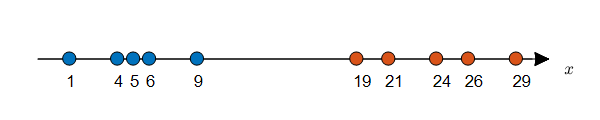
그림 2. Label이 주어진 Density Estimation 문제 (MLE를 이용해 풀 수 있음)
그러면, 이 데이터 셋에 대한 확률 분포를 추정 할 수 있을까?
여러가지 방법으로 확률 분포를 추정 할 수 있지만, 모수적인 방법으로 확률 분포를 추정 한다고 하면 우선 분포를 가정하고 거기에 맞는 모수들을 추정해야 한다. 앞서 언급한 방법인 최대우도법(MLE)은 주어진 데이터에 대해 분포의 모수를 추정할 수 있게 해주는 아주 좋은 방법이라고 할 수 있다. 아래의 그림 3은 그림 2에서 주어진 데이터들에 대해 정규분포를 가정하고 모수를 추정해 확률 분포를 추정한 결과라고 할 수 있다. 모수 추정 방법은 앞서 언급한 MLE의 결과를 이용하여 각 label에 해당하는 데이터들의 평균값과 표준편차 값을 계산함으로써 진행될 수 있다.
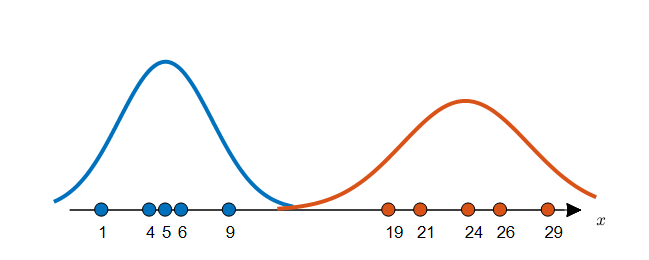
그림 3. label이 주어진 데이터와 이에 대해 추정한 두 분포
그런데, 만약 우리에게 label이 주어지지 않는다면 어떨까?
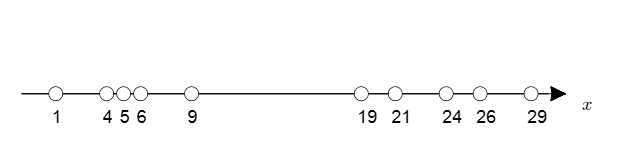
그림 4. label이 주어지지 않은 데이터들의 분포
위의 그림 4에서는 그림 2와 같은 데이터에 라벨이 주어지지 않은 경우를 보여주고 있다.
라벨을 부여하기 위해선 확률 분포가 필요한데, 확률 분포를 얻기 위해선 모수를 알아야 하고, 모수를 알기 위해선 다시 각 데이터에 라벨이 필요하다.
다시 말해 우리에게 주어진 문제는 닭이 먼저냐 달걀이 먼저냐의 문제와 같다.
따라서 우리가 할 수 있는 일은 랜덤하게 라벨을 주고 시작하던지, 랜덤하게 분포를 설정해주고 시작하던지 둘 중 하나이다.
우리는 각 라벨에 해당하는 분포를 랜덤하게 주어주고 시작해보도록 하자.
이 때, 분포는 각 라벨별 모수($\mu, \sigma$)를 선정하고 그에 따라 각 라벨에 대한 분포를 주어주고자 한다.
두 개의 분포가 주어졌다고 하면, 각 데이터에 대한 분포의 높이값(즉, likelihood)을 비교하여 라벨링을 해줄 수 있다.
주황색과 파란색을 각각 그룹 1, 그룹 2라고 했을 때, 각 그룹의 평균과 표준편차는 다음과 같았다고 해보자.
\[\mu_1 = 3, \sigma_1 = 2.9155\] \[\mu_2 = 10, \sigma_2 = 3.9623\]그럼 각 라벨에 대해 그림 5와 같은 분포를 확인할 수 있게 된다.
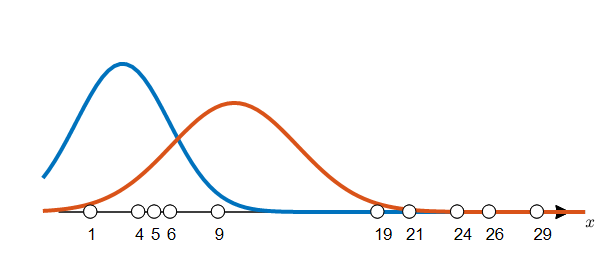
그림 5. 두 label(0, 1)에 대한 분포가 만약에 주어진다면?
위의 그림 5와 같은 분포가 random 하게 주어졌다고 하면 그 분포에 맞추어서 각각의 데이터들의 label을 선정할 수 있다. 아래의 그림 6에서는 $x=9$인 데이터 샘플의 label을 선정하고자 하는 과정을 보여주고 있다.
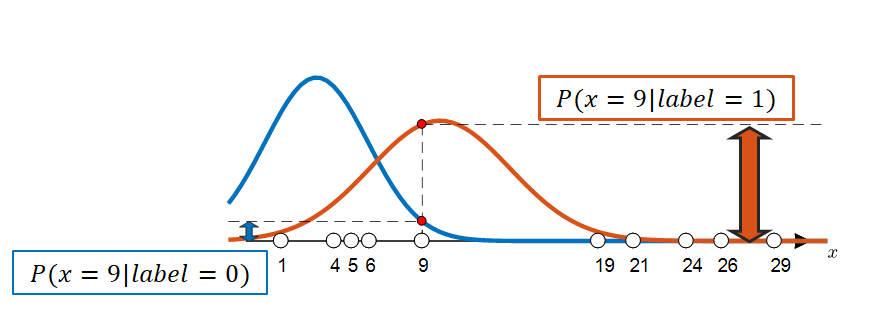
그림 6. 주어진 분포를 이용해 각각의 데이터 샘플들의 라벨을 선정할 수 있다. 이 경우 $x = 9$에 해당하는 데이터의 label은 1이 될 것이다.
그림 6의 방법을 이용하여 모든 데이터 샘플들에 대한 label을 확인하면 다음의 그림7과 같은 결과를 얻을 수 있을 것이다.
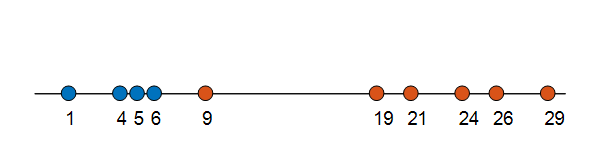
그림 7.
자 그럼 이번에는 그림 7에서 확인한 label에 따라 각 그룹의 분포를 예측해보자.
각 그룹의 평균, 표준편차는 다음과 같다.
\[\mu_1 = 4, \sigma_1 = 2.1602\] \[\mu_2 = 21.33, \sigma_2 = 7.0048\]이 값을 이용해 각 그룹의 분포를 그려보면 다음과 같다.
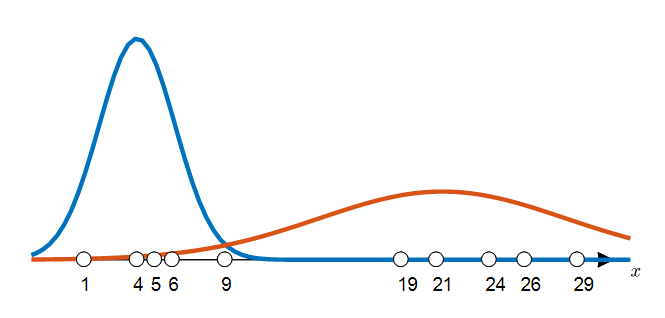
그림 8.
그림 5와 그림 8을 비교해보면 분명히 분포가 바뀐 것을 확인할 수 있을 것이다.
그러면 우리는 또 다시 이렇게 바뀐 분포를 이용해 라벨링을 새롭게 바꿀 수 있고, 이 과정을 계속 수행하다보면 결국 분포는 수렴할 것이라고 예상할 수 있다.
그 과정을 그림 한장으로 요약하면 대략적으로 다음과 같다.
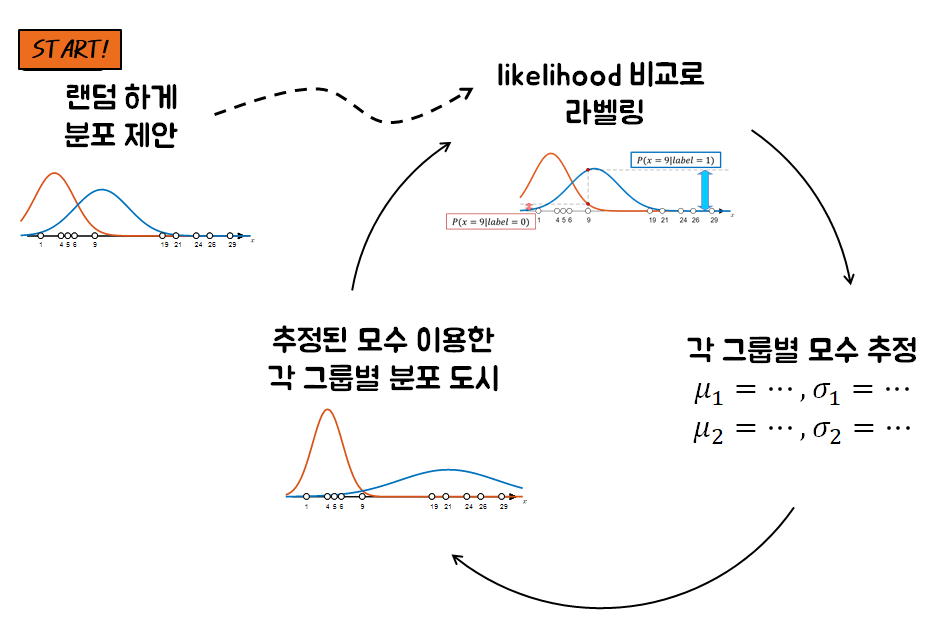
그림 9. label이 주어져있지 않은 경우 clustering을 수행할 수 있는 방법
이러한 방법을 여러번 수행하게 되었을 때의 결과는 아래의 영상에서 확인할 수 있다.
아래 영상에서는 epoch = 10까지만 반복을 수행하였지만, 분포가 수렴하지 않아 추가 반복이 필요한 경우 얼마든지 iteration 수는 늘릴 수 있다.
그림 10. label이 없이 주어진 데이터에 대한 clustering 수행 과정
이와 같은 방식으로 label이 주어져있지 않은 데이터에 대해 데이터셋은 정규분포를 이룰 것이라 가정하고 clustering을 수행해주는 과정을 Gaussian Mixture Modeling이라고 한다.
EM 알고리즘과 GMM
이전 꼭지에서 우리가 처한 문제와 해결 방법에 대해서 생각해보았다.
다시 정리하자면, 우리가 처한 문제는 라벨이 없는 데이터들이 주어졌다는 점이었으며, 우리가 필요한 해답은 각 라벨 별 분포였다.
이 문제가 어려운 이유는 라벨을 얻기 위해선 분포가 필요하고, 분포를 얻기 위해선 라벨이 필요하기 때문이었다.
문제의 해결을 위해 우리는 데이터 셋들이 정규분포를 이룰 것이라 가정했다. 그런 뒤, 랜덤하게 모수를 주어준 뒤 라벨을 얻고, 그 라벨들을 이용해 다시 분포를 얻는 방식으로 clustering을 수행하였다.
(이러한 clustering 방식을 Gaussian Mixture Modeling이라고 부른다는 것은 덤이다.)
이것은 일반적으로 EM-알고리즘이라고 하는 알고리즘의 응용 중 하나라고 할 수 있다.
EM 알고리즘은 Expectation-Maximization의 약자인데,
여기서 Expectation은 로그 가능도의 기댓값을 계산하는 과정이다 라고 하는데, 그냥 라벨을 찾는 과정이라고 보면 좋을 것 같고
Maximization은 Maximum Likelihood Estimation을 수행해서 모수를 추정하는 과정이라고 볼 수 있다.
즉, E-step에서는 “변수의 정보(즉, 이 변수의 라벨은?)”를 업데이트 하고, M-step에서는 “변수들이 어떻게 분포 되어 있는지에 대한 가설”을 업데이트하는 과정이라고 봐도 좋을 것 같다.
아래는 EM 알고리즘의 관점에서 GMM 알고리즘의 흐름을 수식적으로 풀어 쓴 것이다.
Repeat until convergence: {
$\quad$(E-step) For each $i$, $j$, set
\[w_j^{(i)} := p(z^{(i)} = j|x^{(i)};\phi,\mu,\Sigma)\]$\quad$(M-step) Update the parameters:
\[\phi_j := \frac{1}{m}\sum_{i=1}^{m}w_j^{(i)}\] \[\mu_j := \frac{\sum_{i=1}^{m}w_j^{(i)}x^{(i)}}{\sum_{i=1}^{m}w_j^{(i)}}\] \[\Sigma_j := \frac{\sum_{i=1}^{m}w_j^{(i)}\left(x^{(i)}-\mu_j\right)\left(x^{(i)}-\mu_j\right)^T}{\sum_{i=1}^{m}w_j^{(i)}}\]}
여기서 $i$는 데이터의 순번, $j$는 라벨을 의미하며, $x^{(i)}$는 $i$번째 데이터셋, $z^{(i)}$는 $i$번째 데이터셋의 라벨을 의미한다.
또 $w_j^{(i)}$는 $i$번째 데이터가 $j$번 그룹에 속할 확률을 의미한다.
$\phi$는 그룹들 간의 데이터 비율을 의미한다. 가령, 0번 그룹과 1번 데이터는 6:4로 존재한다고 하면 $\phi = [0.6, 0.4]$이다.
$\mu_j$는 $j$번 그룹의 평균값을 의미하고, $\Sigma_j$는 표준편차 혹은 공분산행렬을 의미한다.
복잡해 보이는 것들이 많아 보이지만, 하나 하나 뜯어 보면서 생각해보자.
E-step 분해
GMM 파트에서 설명하였지만, EM 알고리즘을 시작하기 위해서는 처음의 random initialization이 필요하다.
EM 알고리즘의 flow 중 (E-step)을 먼저 보면, $w_j^{(i)} := p(z^{(i)} = j|x^{(i)};\phi,\mu,\Sigma)$라는 식에는
$\phi, \mu, \Sigma$를 이미 주어진 파라미터로 생각한다는 것을 알 수 있다.
$\phi$에 대해서는 차츰 더 설명하겠지만 각 label별 weight의 합이라고 보면 된다. 우선은 $[0.5, 0.5]$와 같이 각 라벨 별로 initialize해도 좋다.
$\mu$와 $\Sigma$는 각각 평균과 분산에 관한 식이다. 분산의 $\Sigma$는 그리스 알파벳 대문자로 쓰여있는데, 그 이유는 입력의 차원이 높아지면 공분산까지 함께 생각해야 하기 때문이다.
다시 말해 $\sigma$는 표준편차를 나타내지만 $\Sigma$는 공분산행렬을 나타낸다. 지금은 복잡하게 보일 수 있기 때문에 그냥 1차원에서는 $\Sigma$는 표준편차다 라고 생각하고 넘어가도 좋다.
$\mu$와 $\Sigma$는 그림 5에서 처럼 랜덤하게 주어주고 initialize 해주면 충분하다.
(local maxima에 빠지는 문제에 대해서는 지금 당장은 고려하지 않도록 하자.)
그럼 $w_j^{(i)} := p(z^{(i)} = j|x^{(i)};\phi,\mu,\Sigma) $라는 식에서 $\phi, \mu, \Sigma$에 대해 알아보았다면, $w_j^{(i)} := p(z^{(i)} = j|x^{(i)})$라는 식은 어떻게 해석해야 할까?
그것은 우리에게 $x^{(i)}$라는 데이터가 주어졌고, $\phi, \mu, \Sigma$ 라는 모수를 줌으로써 각 label에 대한 확률 분포를 가정했을 때
그 분포의 높이에 따라 $(i)$번째 데이터가 $j$번 그룹에 속할 확률을 계산하겠다는 뜻이다.
예를 들어 $w_j^{(i)}$라는 값은 그룹이 총 3개 였다고 하고, 0, 1, 2번 그룹에 속할 확률이 각각 0.8, 0.15, 0.05라고 한다면
\[w_0^{(i)} = p(z^{(i)} = 0|x^{(i)}) = 0.8\] \[w_1^{(i)} = p(z^{(i)} = 1|x^{(i)}) = 0.15\] \[w_2^{(i)} = p(z^{(i)} = 2|x^{(i)}) = 0.05\]라고 쓸 수 있는 것이다. (i번째 데이터에 대해서 각 그룹에 속할 확률을 모두 더하면 1이 되어야 한다는 점도 빠뜨리지 말자.)
여기서 조금 더 구체적인 확률 계산은 베이즈 정리에 따라 수행할 수 있다.
식은 복잡해 보이지만, 해당 label에 포함될 Prior x likelihood 값을 각 label에 포함될 Prior x likelihood 값을 모두 더한 값으로 나눈 것이 $(i)$번째 데이터가 $j$번 그룹에 속할 확률이 된다.
식을 써보자면 다음과 같다.
\[p(z^{(i)}=j|x^{(i)};\phi,\mu,\Sigma) =\frac{p(x^{(i)}|z^{(i)} = j; \mu, \Sigma)p(z^{(i)}=j;\phi)}{p(x^{(i)};\phi, \mu, \Sigma)}\] \[= \frac{p(x^{(i)}|z^{(i)} = j; \mu, \Sigma)p(z^{(i)}=j;\phi)}{\sum_{k=1}^{l}p(x^{(i)}|z^{(i)} = k; \mu, \Sigma)p(z^{(i)}=k;\phi)}\]M-step 분해
E-step을 잘 이해하고 나면 M-step은 어려울 것이 없다.
M-step에서는 E-step에서 계산한 $w_j^{(i)}$ 값들을 이용해 모수를 추정하는 과정이다.
이 모수들은 최대우도법을 이용하여 모두 쉽게 계산할 수 있다. ($x^{(i)}$는 모두 주어진 데이터라는 점을 꼭 생각하자.)
앞서 설명한 것 처럼 $\phi$는 그룹들 간의 데이터 비율, $\mu_j$는 $j$번 그룹의 평균값, $\Sigma_j$는 표준편차 혹은 공분산행렬을 의미한다.
그런데, 정확히 말하면 $\phi$는 사전 확률과 관련 있는 값이라고 할 수 있는데, $\phi$는 각 그룹별 평균 소속 확률이다.
가령, 아래의 그림과 같이 10개 데이터가 있었다고 하면 $w_j^{(i)}$에 대해 $\phi$를 계산할 수 있다.
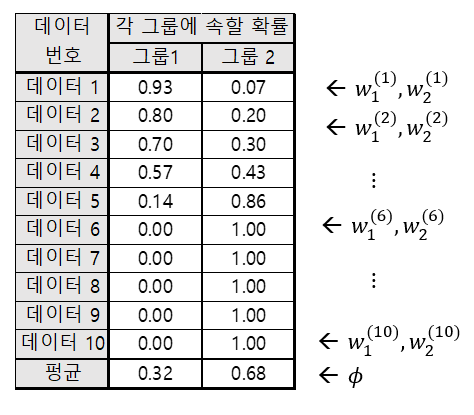
그림 11. 주어진 $w$에 대해 $\phi$를 계산하는 방법
M-step에서의 수식의 계산은 어렵지 않으나, 혹시나 부족하다고 생각하면 아래의 MATLAB 코드를 좀 더 참고해보도록 하자.
MATLAB code
아래에는 MATLAB을 이용해 GMM 알고리즘을 EM 알고리즘 관점에서 작성하였다.
이 과정에서는 7:3의 비율로 가상의데이터를 만들고, 평균은 각각 0과 15로 주어놓고자 한다.
코드의 하단에는 실행 시 영상이 첨부되어 있으므로 확인하는 것도 좋을 것으로 보인다.
clear; close all; clc;
% GMM 알고리즘 수동으로 코드 작성
%% Make Synthetic Data
% 가상의 데이터를 만들고자 함. 데이터는 두 개의 그룹으로 나눌 것이며, 평균은 0, 15와 같이 조금 멀리 떨어뜨려놓을 생각.
% 각 그룹의 비율은 7:3으로 진행하고자 함. 즉, phi = [0.7, 0.3]으로 진행.
% 데이터 만들어주기
rng(1)
mu = [0, 15];
vars = [12, 3];
n_data = 1000;
phi = [0.7, 0.3];
X = [];
for i_data = 1:n_data
if rand(1) < 0.7
X(end+1) = randn(1) * sqrt(vars(1)) + mu(1);
else
X(end+1) = randn(1) * sqrt(vars(2)) + mu(2);
end
end
% 데이터 분포 확인
figure('position',[628, 334, 774, 577],'color','w');
histogram(X, 50,'Normalization','pdf')
xx = linspace(-30, 30, 100);
yy1 = normpdf(xx, mu(1), sqrt(vars(1)));
yy2 = normpdf(xx, mu(2), sqrt(vars(2)));
hold on;
grid on;
plot(xx, yy1 * phi(1)+ yy2 * phi(2), 'k','linewidth',2); % 즉, phi = [0.7, 0.3]
xlabel('x');
ylabel('pdf');
%% GMM 알고리즘 작성
clear h
my_normal = @(x, mu, sigma) 1/(sigma * sqrt(2*pi)).*exp(-1 * (x-mu).^2/(2*sigma^2));
% random initialization
est_mu = [-25, 20];
est_vars = [7, 9.5];
est_w = zeros(n_data, 2);
est_phi = [0.5, 0.5];
est_yy1 = normpdf(xx, est_mu(1), sqrt(est_vars(1)));
est_yy2 = normpdf(xx, est_mu(2), sqrt(est_vars(2)));
h1 = plot(xx, est_yy1 * est_phi(1), 'r','linewidth',4);
h2 = plot(xx, est_yy2 * est_phi(2), 'g','linewidth',4);
t = text(-27, 0.075, 'the first initialization','fontsize',12);
pause;
delete(t);
delete(h1);
delete(h2);
% GMM iteration
n_iter = 50;
for i_iter = 1:n_iter
%%%%%%%%%%%%%%%%%%%%%%%%%%% E-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i_data = 1:n_data
l1 = my_normal(X(i_data), est_mu(1), sqrt(est_vars(1)));
l2 = my_normal(X(i_data), est_mu(2), sqrt(est_vars(2)));
est_w(i_data, 1) = (l1 * est_phi(1)) / (l1 * est_phi(1) + l2 * est_phi(2));
est_w(i_data, 2) = (l2 * est_phi(2)) / (l1 * est_phi(1) + l2 * est_phi(2));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%% E-step 끝 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%% M-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% phi 추정
est_phi = 1/n_data * sum(est_w, 1);
% mu 추정
est_mu(1) = (X * est_w(:,1))/sum(est_w(:,1));
est_mu(2) = (X * est_w(:,2))/sum(est_w(:,2));
% Sigma 추정
est_vars(1) = sum(est_w(:,1)'.*(X-est_mu(1)).^2)/sum(est_w(:,1));
est_vars(2) = sum(est_w(:,2)'.*(X-est_mu(2)).^2)/sum(est_w(:,2));
%%%%%%%%%%%%%%%%%%%%%%%%%%% M-step 끝 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 아래는 그림 그리기 위한 용도
est_yy1 = normpdf(xx, est_mu(1), sqrt(est_vars(1)));
est_yy2 = normpdf(xx, est_mu(2), sqrt(est_vars(2)));
h1 = plot(xx, est_yy1 * est_phi(1), 'r','linewidth',4);
h2 = plot(xx, est_yy2 * est_phi(2), 'g','linewidth',4);
t = text(-27, 0.075, ['Epoch: ',num2str(i_iter),' / ',num2str(n_iter)],'fontsize',12);
pause;
if i_iter < n_iter
delete(t);
delete(h1);
delete(h2);
end
end
그림 11. 인위적으로 생성한 데이터에 대한 GMM clustering MATLAB 코드 수행 과정.