본 포스팅은 MIT의 Patrick H. Winston 교수님의 강의를 정리한 것임을 밝힙니다.
1. n-차원 공간에서 벡터를 이용한 hyperplane의 표현
hyperplane이란 ‘a subspace of one dimension less than its ambient space’로 정의된다.1
즉 n차원의 공간에서의 hyperplane은 n-1차원의 subspace를 의미하는 것이며, 3차원의 경우 hyperplane은 2차원의 면이 되고, 2차원의 경우는 hyperplane은 1차원의 선이된다. 복잡한 문제에 대해 쉽게 접근하기 위해 3차원과 2차원의 hyperplane의 방정식에 대해 생각해보고 이것을 n차원에 대해 일반화 시켜보도록 하자.
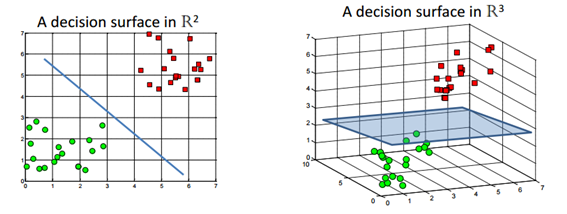
그림 1. Decision surface. 출처 : Support Vector Machines without tears
평면의 방정식은 다음과 같다. 법선 벡터 $\vec{v}=(a,b,c)$에 대해서 원점과의 거리가 $d$인 평면의 방정식은 $ax+by+cz+d=0$이다. 그렇다면, 2차원의 경우를 생각해보자. 이것을 그대로 적용시킨다면 직선의 방정식은 직선에 수직한 벡터 $\vec{w}=(a,b)$에 대해 원점과의 거리가 d인 직선의 방정식은 $ax+by+d=0$이 될 것이다.
다시 이것을 약간만 고쳐보면 $y=-\frac{a}{b}x-\frac{d}{b}$임을 쉽게 알 수 있으며, 이 1차 함수의 기울기는 벡터$\vec{w}$ 와 수직이라는 사실을 알 수 있다. 따라서 법선 벡터와 임의의 실수 를 이용하면 n차원 공간에서의 hyperplane을 쉽게 생각해낼 수 있다.
이러한 사실을 이용하면 n차원의 실수 공간에서 hyperplane은 다음과 같이 정의할 수 있다.
Definition 1. Hyperplane2
Let $a_1,a_2,\cdots,a_n$ be scalars not all equal to 0. Then set consisting of all vectors
\[X = \begin{bmatrix} x_1\\ x2\\ \vdots \\x_n \end{bmatrix}\in\Bbb{R}^n\]such that
\[a_1x_1 + a2_x2 + \cdots + a_nx_n = c\]for c a constant is a subspace of $R^n$ called a hyperplane.
2. 라그랑주 승수법에 대한 이해
라그랑주 승수법은 최적화 문제에서 사용되는 수학적 기법으로써 최대 또는 최소값을 찾으려는 문제에서 해결방법으로 사용된다. 라그랑주 승수법을 사용하는 방법은 목적 함수 $f(x,y)$와 제약 조건 $g(x,y)=0$에 대해 새로운 변수 $\lambda$를 이용하여 다음의 보조 방정식을 만든 다음, 보조방정식에 대해 모든 변수에 대한 편미분 값이 0이되는 변수의 해를 찾는 것이다.
\[L(x, y, \lambda) = f(x,y) - \lambda g(x,y)\]이렇게 목적 함수와 제약 조건에 대해 위와 같은 보조 방정식을 만들고 문제를 풀 수 있게 되는 이유는 제약 조건을 만족시키면서 목적 함수를 최대화 또는 최소화 시키는 점에서는 목적함수의 gradient(쉽게 말해 기울기)와 제약 조건의 gradient가 평행하기 때문이다. 아래의 그림을 보면서 조금 더 자세하게 알아보자.
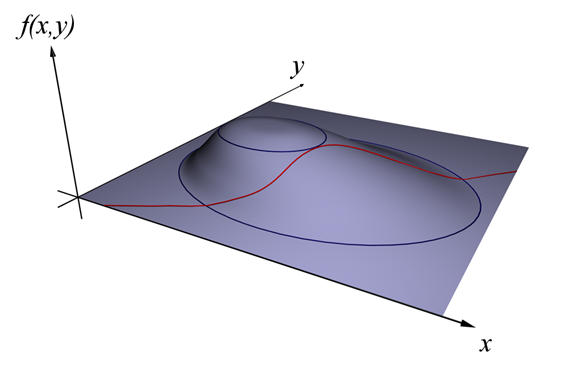
그림 2. 라그랑주 승수법에 대한 설명 (1). 출처 : 위키피디아
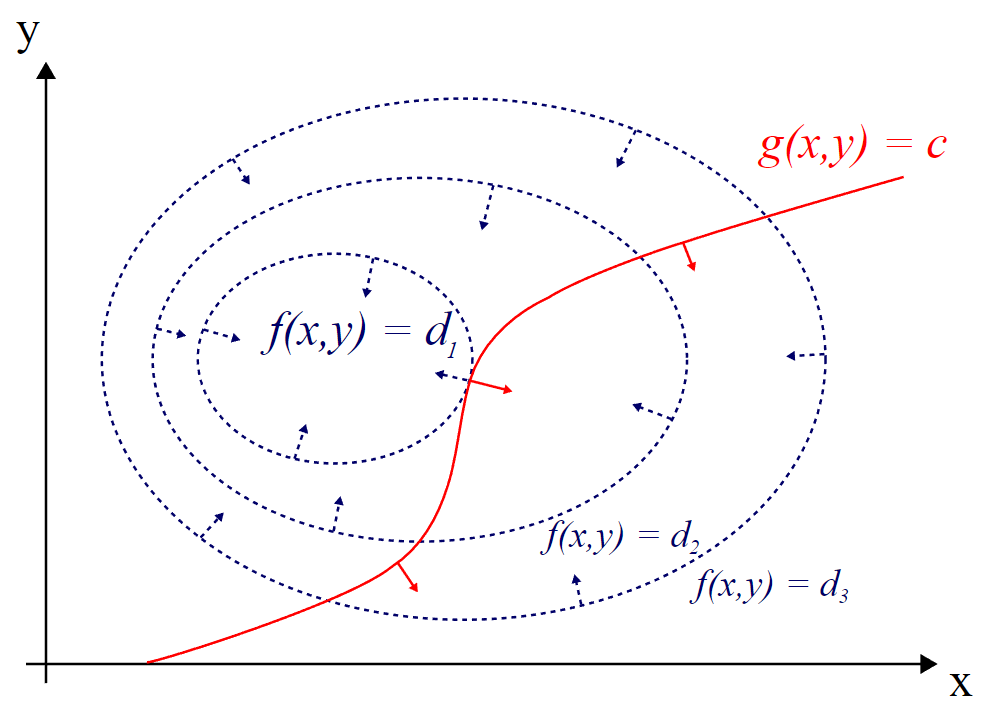
그림 3. 라그랑주 승수법에 대한 설명 (2). 출처 : 위키피디아
그림 2, 3에서 $f(x,y)$가 $d_1$이라는 값에서부터 $d_3$라는 값 까지 변할 수 있는데, $g(x,y)=c$라는 제약 조건이 붙었다고 하자. 그렇다면 $g(x,y)=c$라는 제약조건을 만족시키면서 $f(x,y)$가 커질 수 있는 최대값은 얼마일까? 물론 $d_1$일 것이다.
그림 3을 유심히 관찰하면 $f(x,y)$와 $g(x,y)=c$가 접점을 이루는 곳이 제한된 조건을 만족하는 $f(x,y)$의 최대값이라는 것을 알 수 있다. 그렇다면 접점을 찾는 조건은 무엇일까? 바로 두 곡선의 기울기가 접점에서 평행을 이룬다는 사실이다. 곡선의 기울기는 미분을 통해 알 수 있는데 변수가 많아지면 편미분을 통해서, 조금더 자세하게는 gradient를 통해서 구할 수 있다. 즉, 접점의 값을 구하는 조건은 아래와 같다.
\[\nabla_{x, y}f = \lambda\nabla_{x, y}g\]where
\[\nabla_{x,y}f = \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right)\] \[\nabla_{x,y}g = \left(\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}\right)\]또한, 일반적으로 여러개의 제약 조건이 붙는 경우에는 다음과 같이 만들 수도 있을 것이다.
\[L(x_1, \cdots, x_n, \lambda_1, \cdots, \lambda_M) = f(x1,\cdots, x_n)-\sum_{k=1}^M{\lambda_kg_k(x_1,\cdots,x_n)}\]즉 이러한 경우에는 다음 식의 해를 구하게 되면 최적화 조건을 찾을 수 있게 되는 것이다.
\[\nabla_{x_1, \cdots, x_n,\lambda_1,\cdots,\lambda_M}L(x_1, \cdots, x_n, \lambda_1,\cdots, \lambda_M) = 0 \Leftrightarrow \begin{cases}\nabla f(x)-\sum_{k=1}^{M}\lambda_kg_k(x) \\g_1(x) = \cdots = g_M(x) = 0 \end{cases}\]3. 서포트 벡터 머신
가. Decision Rule
Decision rule이란 새로운 입력 $\vec{u}$에 대해서 이 입력의 class가 + 인지 - 인지 결정하는 방법에 대한 것이다. 다음과 같이 2차원 공간 위에 decision boundary(hyperplane)와 법선 벡터 $\vec{w}$가 있다고 하자.
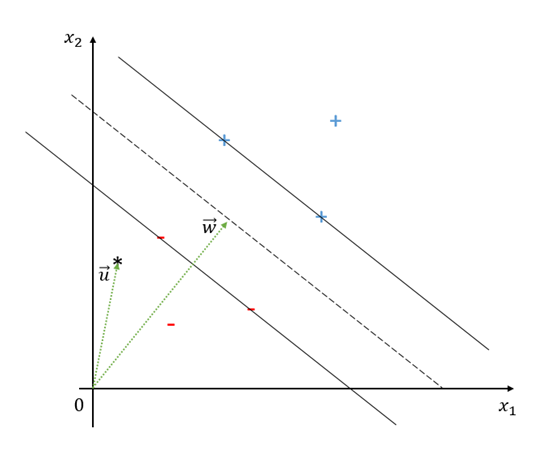
그림 4. Decision boundardy와 decision rule
아직 $\vec{w}$가 무엇인지는 모르지만 우리가 설정하려고 하는 것은 가운데 dashed line 보다 위에 있으면 +로, 아래에 있으면 -로 classify하려는 것이다. 즉, 우리는 decision rule을 다음과 같이 설정할 수 있다.
\[\vec{w}\cdot\vec{u} \geq c\]이 때 c는 임의의 상수이다. 즉, 아직 $\vec{w}$와 c가 정해진 값은 아니지만 이 조건을 만족하면 +라고 하자라고 decision rule을 정할 수 있는 것이다. 이 식을 약간 변형시키면,
\[\vec{w}\cdot\vec{u}+b\geq 0\]으로 변형시킬 수 있다. 이 식은 2차원에서의 직선을 의미하지만, 첫 번째 장에서 보았던 hyperplane으로 확장해 생각할 수 있다. 이제 우리가 알아야 하는 것은 $\vec{w}$와 $b$이다.
나. 서포트 벡터와 street 생성에 대한 조건
이제 training에 대한 이야기가 시작된다. 두 가지의 클래스로 샘플들이 구별 되어 있다고 하자. 하나는 positive samples($x_+$), 나머지 하나는 negative samples($x_-$)이다.
식 (10)으로부터 positive, negative samples에 대한 조건으로 확장해보자.
다시 그림 4을 보자. 우선 실선으로 표시된 두개의 선 위에 positive samples와 negative samples가 걸쳐있다는 것을 알 수 있다.
또, 실선들 사이에 있는 dashed line으로부터 실선까지의 거리는 같게 설정했다.
따라서 우리는 이렇게 생각할 수 있다. 식 (10)이 표현하는 dashed line은 최대한 가까운 positive samples와 negative samples로부터 동일하게 $\delta$만큼 떨어져야 한다. 그리고 가장 가까운 positive, negative samples가 아니면 $\delta$보다 크게 떨어져야 한다.
그러므로 다음의 두 식을 생각할 수 있다.
\[\vec{w}\cdot\vec{x}_++b \geq \delta\] \[\vec{w}\cdot\vec{x}_-+b \leq -\delta\]그런데, 어차피 $\vec{w}$도 모르는 수이고 $b$도 모르는 수이기 때문에 임의의 $\delta$로 나누어주어도 임의의 숫자이다. 그러므로 $\delta$에 대해 정규화하여서 다음의 수식을 얻을 수 있다.
\[\vec{w}\cdot\vec{x}_++b \geq 1\] \[\vec{w}\cdot\vec{x}_-+b \leq -1\]이제 수학적 트릭을 약간 사용해보자. 방금 유도한 두 개의 식을 하나로 묶을 수 있는 변수
\[y_i=\begin{cases}+1 &&\text{ for } x_+ \\ -1 && \text{ for } x_- \end{cases}\]를 생각하자. 그러면 식(13)과 식 (14)는 다음과 같이 합칠 수 있다.
\[y_i(\vec{w}\cdot\vec{x}_i+b)\geq 1\]이 식을 조금만 변형하면 hyperplane으로부터 가장 가깝게 있어서 그림 4의 실선 위에 있게 되는 samples에 대한 조건은 다음과 같게 된다.
\[y_i(\vec{w}\cdot\vec{x}_i+b)-1 = 0\]다. Street의 너비와 최적화 문제 설정
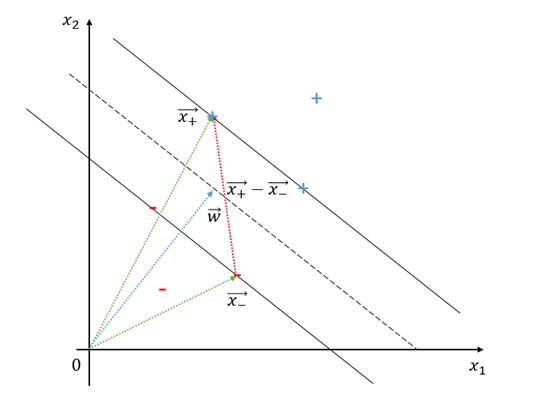
그림 5. Street의 너비를 구하는 과정
그림 5에서 실선 위에 있는 $x_+$와 $x_-$에 대한 원점으로부터의 벡터 $\vec{x_+}$와 $\vec{x_-}$에 대하여, $\vec{x_+}-\vec{x_-}$를 생각해보자. 이것을 이용해서 두 실선 사이의 거리를 생각할 수 있다. $\vec{w}$는 dashed line에 수직하기 때문에 $\vec{w}$와 방향은 같고 크기는 1인 벡터를 이용하면 두 실선 사이의 거리를 생각할 수 있다. 두 실선사이의 거리는
\[\frac{\vec{w}}{|\vec{w}|}\cdot(\vec{x}_+ - \vec{x}_-)\]이다.
다시 한번 식(17)로 부터 $x_i$가 positive sample이었다면 $y_i=1$이고 negative sample이었다면 $y_i=-1$이기 때문에
\[\vec{w}\cdot\vec{x}+b-1 = 0\] \[\Rightarrow \vec{w}\cdot\vec{x}_i = 1-b\]이고,
\[\vec{w}\cdot\vec{x}+b+1 = 0\] \[\Rightarrow \vec{w}\cdot\vec{x}_i = -1-b\]이다. 다시 이것을 식 (18)에 대입해보자.
\[식(18) \Rightarrow \frac{1}{|\vec{w}|}(\vec{w}\cdot\vec{x}_+ - \vec{w}\cdot\vec{x}_-)\] \[=\frac{1}{|\vec{w}|}(1-b+1+b)\] \[=\frac{2}{|w|}\]즉, 두 실선 사이의 거리는 $\frac{2}{|\vec{w}|}$이며, 우리의 목표는 $\frac{2}{|\vec{w}|}$를 최대화 하는 것이라고 할 수 있다. 또는 상수를 떼면 $max\frac{1}{|\vec{w}|}$ 또는 $min|\vec{w}|$라고도 바꿀 수 있으며, 수학적인 편의를 위해 이것을
\[min\frac{1}{2}|\vec{w}|^2\]로도 바꿀 수 있을 것이다.
라. 라그랑주 승수법과 constraints 유도
따라서, 우리가 처한 최적화 문제는 다음과 같다.
\[\text{조건(constraints): } y_i(\vec{w}\cdot\vec{x}_i+b)-1 = 0\] \[\text{목적함수 :} \frac{1}{2}|\vec{w}|^2\]따라서, 다음의 보조방정식을 세울 수 있다.
\[L = \frac{1}{2}|\vec{w}|^2 -\sum_i \alpha_i\left[y_i(\vec{w}\cdot \vec{x}_i +b) -1\right]\]이제 변수들로 보조방정식을 편미분해보자.
\[\frac{\partial L}{\partial \vec{w}} = \vec{w}-\sum_i \alpha_i y_i x_i = 0\] \[\vec{w} = \sum_i \alpha_i y_i \vec{x}_i\]그러므로 $\vec{w}$는 몇 개의 $\vec{x_i}$들의 선형 합(linear sum)이다. ‘몇 개의(some)’라고 말하는 것은 $\alpha_i=0$인 경우에는 합에 포함되지 않을 수 있기 때문이다. 그 말은 그림 4에서 본 바와 같이 실선 위에 있지 않아서 실선을 설정하는데 도움을 주지 않는 sample들에 대한 $\alpha$의 값은 0이 되게 하는 알고리즘이 설계한다는 것이다.
이제 식(31)을 최초의 boundary decision에 대해 생각해보면 다음과 같은 constraints를 얻게 된다.
\[\sum_i \alpha_i y_i \vec{x}_i\cdot\vec{u}+b = +1\text{ for positive class}\] \[\sum_i \alpha_i y_i \vec{x}_i\cdot\vec{u}+b = -1\text{ for negative class}\](여기서, 다시 한번 $\pm 1$의 값만 우변에 나오는 것은 실선 위에 있지 않는 점들에 대한 alpha 값은 모두 0이 되어 버리기 때문이다.)
식 (29)에 대한 또 하나의 편미분은 다음과 같다.
\[\frac{\partial L}{\partial b}=-\sum_i\alpha_i y_i = 0\] \[\Rightarrow \sum_i \alpha_iy_i = 0\]$\alpha_i$에 대해서는 편미분 해주게 되면 무조건 0이 되므로 $\alpha_i$의 값을 구하기 위해서는 다른 방법을 이용해야 한다.
$\alpha_i$를 구하기 위해서는 식 (32), (33), (35)를 놓고 연립하면 된다. 그런데, 조금만 더 나아가보자. 세워둔 식 (29)의 보조방정식 $L$에 식 (31)과 식 (35)를 대입해보자.
\[L = \frac{1}{2}|\vec{w}|^2 - \sum_i \alpha_i\left[y_i(\vec{w}\cdot\vec{x}+b])-1\right]\] \[=\frac{1}{2}\left(\sum_i \alpha_i y_i \vec{x}_i\right)\left(\sum_j \alpha_j y_j \vec{x}_j\right) - \sum_i\left(\alpha_iy_i\vec{w}\cdot\vec{x}_i + \alpha_i y_i b - \alpha_i\right)\] \[=\frac{1}{2}\left(\sum_i \alpha_i y_i \vec{x}_i\right)\left(\sum_j \alpha_j y_j \vec{x}_j\right) - \sum_i\left(\alpha_iy_i\vec{x}_i\left(\sum_j\alpha_jy_j\vec{x}_j\right) + \alpha_i y_i b - \alpha_i\right)\] \[=\frac{1}{2}\left(\sum_i \alpha_i y_i \vec{x}_i\right)\left(\sum_j \alpha_j y_j \vec{x}_j\right)-\left(\sum_i \alpha_i y_i\vec{x}_i\right)\left(\sum_j \alpha_j y_j\vec{x}_j\right)-\sum_i\alpha_i y_i b + \sum_i \alpha_i\] \[=\sum_i\alpha_i - \frac{1}{2}\left(\sum_i \alpha_i y_i \vec{x}_i\right)\left(\sum_j \alpha_j y_j \vec{x}_j\right)\] \[=\sum_i\alpha_i - \frac{1}{2}\sum_i\sum_j\alpha_i\alpha_j y_i y_j\vec{x}_i\cdot\vec{x}_j\]마. Kernel Tricks
식 (41)을 보면 L의 최대값은 $\vec{x_i}\cdot\vec{x_j}$에 의해 결정된다. 따라서 $\vec{x_i}\cdot\vec{x_j}$를 적절하게 잘 변형시켜 줄 수 있다면 $L$의 최대값을 더 끌어올려줄 수 있다.
이것을 하는 방법은 $\vec{x_i}$와 $\vec{x_j}$에 대해 적절한 변환을 취해주거나 $\vec{x_i}\cdot\vec{x_j}$를 통째로 적절하게 변형시켜 주는 것이다.
즉, $\vec{x_i}$에 대한 적절한 변환 $\phi(\cdot)$를 찾아주어서 $\vec{x_i}\cdot\vec{x_j}$대신에 $\phi(\vec{x_i})\cdot\phi(\vec{x_j})$를 대입하는 방법이 있을 수 있다.
또는 $\vec{x_i}\cdot\vec{x_j}$에 대해 적절히 대입할 수 있는 변환인 $K(\vec{x_i},\vec{x_j})$를 찾아주어 $\vec{x_i}\cdot\vec{x_j}$대신에 대입할 수도 있다.
수식적으로가 아니라 기하학적으로 해석하면 다음과 같은 그림으로 쉽게 설명할 수 있다.
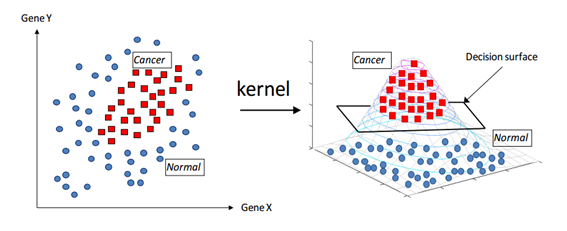
그림 6. Kernel에 대한 기하학적 설명. 출처: Support Vector Machines without Tears
그림 6을 보면 왼쪽 평면에 있는 sample들이 오른쪽과 같이 변형되었는데, 이것은 sample들이 있는 sample 공간을 kernel 함수를 이용하여 공간을 3차원 공간으로 변형시켜주었기 때문이다. 그런 다음 3차원 공간에서 hyperplane을 이용하면 cancer와 normal 샘플들을 좀 더 쉽게 구별할 수 있게 된다.
4. 서포트 벡터 머신 문제 예제.
다음의 + sample과 - sample에 대해서 $\alpha, b, w$의 값을 구하시오.
-ve points : A(0,0), B(1,1) +ve points : C(2,0)
풀이)
+ve points와 -ve points의 위치는 다음과 같다.
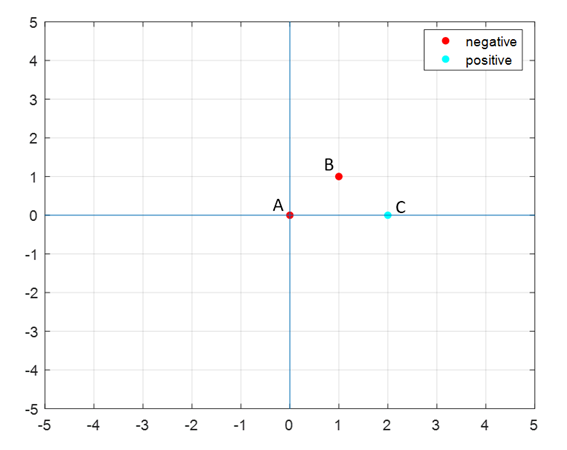
그러므로 눈으로만 봤을 때는 hyperplane의 식은 $y=x-1$정도 될 것으로 보인다. 이것을 대수적으로 확인해보자.
- Step 1) calculate all kernel function values 이 케이스는 kernel function이 특별한 것이 없이 linear kernel이다. 그러므로
이다. 따라서 모든 경우의 수에 대해 다음과 같은 테이블을 구성할 수 있다.

- Step 2) Write out the system of equation
이론을 통해 확인한 constraints는 총 세 가지가 될 수 있겠다.
\[\text{Constraint 1: }\sum_i\alpha_i y_i = 0\] \[\text{Constraint 2: }\sum_i\alpha_i y_i K(x_i, x) + b = 1 \text{ for positive class}\] \[\text{Constraint 3: }\sum_i\alpha_i y_i K(x_i, x) + b = -1 \text{ for negative class}\]따라서, 모든 제한 조건을 가지고 방정식을 적으면 다음과 같이 풀어쓸 수 있겠다.
\[C_1: -\alpha_A - \alpha_B + \alpha_C = 0\] \[C_{3, A}: \alpha_A(-1)K(x_A, x_A) + \alpha_B(-1)K(x_B, x_A) + \alpha_C(+1)K(x_C, x_A) + b = -1\] \[C_{3, B}: \alpha_A(-1)K(x_A, x_B) + \alpha_B(-1)K(x_B, x_B) + \alpha_C(+1)K(x_C, x_B) + b = -1\] \[C_{2, C}: \alpha_A(-1)K(x_A, x_C) + \alpha_B(-1)K(x_B, x_C) + \alpha_C(+1)K(x_C, x_C) + b = 1\]step 1에서 구한 K 값과 위의 네 식을 연립하면
\[\alpha_A = 0, \alpha_B = 1, \alpha_C = 1, b = -1\]이라는 사실을 확인할 수 있다. 그러므로 점 A는 support vector가 아니라는 사실도 알 수 있다.
그리고 $\vec{w}$는
\[\vec{w} = \sum_i\alpha_i y_i\vec{x}_i\] \[=\alpha_A y_i \vec{x}_A + \alpha_B y_i \vec{x}_B + \alpha_C y_i \vec{x}_C\] \[= 0 + (1)(-1)\begin{bmatrix}1 \\1 \end{bmatrix} + (1)(1)\begin{bmatrix}2 \\0\end{bmatrix}\] \[=\begin{bmatrix}1 \\ -1\end{bmatrix}\]이다.
그러므로 hyperplane의 방정식은
\[\vec{w}\cdot\vec{x}+b = 0\]이므로, 이것은
\[x_1-x_2 - 1 = 0\]이고, 쉽게 직선의 방정식으로 나타내면
\[y = x - 1\]이다.
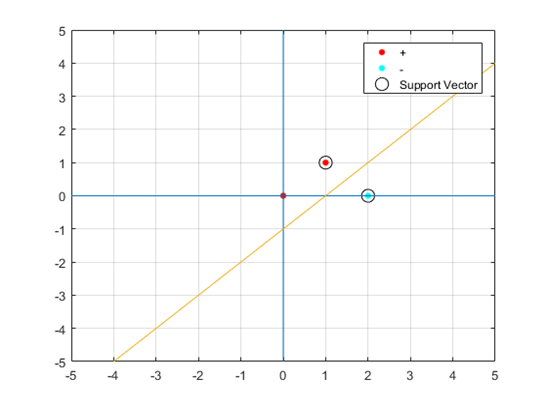
이 결과는 MATLAB의 fitcsvm 함수를 사용한 결과와도 일치한다.
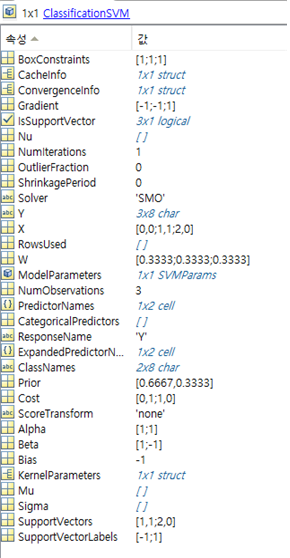
fitcsvm의 결과 모델인데, 여기서 beta는 $\vec{w}$를 의미하고 bias는 우리가 hyperplane 방정식에서 썼던 b를 의미한다.
5. Appendix (MATLAB code)
clear all; close all; clc;
X=[0 0;1 1;2 0];
Y=['negative';'negative';'positive'];
SVMModel=fitcsvm(X,Y);
sv = SVMModel.SupportVectors;
figure
gscatter(X(:,1),X(:,2),Y)
hold on
plot(sv(:,1),sv(:,2),'ko','MarkerSize',10)
legend('+','-','Support Vector')
grid on;
xlim([-5 5])
ylim([-5 5])
line([-5 5],[0 0])
line([0 0],[-5 5])
w=SVMModel.Beta
b=SVMModel.Bias
% 그러니까 식은 1*x+(-1)*y-1=0
% y=x-1임.
x=linspace(-5,5,100);
y=-1*(w(1)/w(2))*x+b;
plot(x,y)