자연상수 $e$의 정의
우선은 자연상수 $e$의 정의와 그 값에 대해 알아보면 다음과 같다.
| DEFINITION 1. 자연상수 $e$ |
|---|
$$e = \lim_{n\rightarrow \infty}\left(1+\frac{1}{n}\right)^n$$ 또한, 소수로 나타낸 e의 근사값은 다음과 같다. $$e = 2.71828 18284 59045 23536 \cdots$$ |
자연상수 $e$는 숫자만 놓고 보기엔 매우 부자연스러워 보이지만 어떤 이유에서 필요했기에 저런 상수를 도입했을까?
마치, 파이($\pi$)도 숫자로만 생각하면 3.14159 265359 … 와 같이 아무런 의미 없어보이는 값이지만 사실은 원의 둘레, 넓이 등을 계산하는데 도움을 주는 값인것처럼 자연 상수 $e$ 역시 어떤 의미가 있을 것이다.
자연상수 $e$의 의의
자연상수 $e$는 자연의 연속 성장을 표현하기 위해 고안된 상수라고 할 수 있다.
조금 더 구체적으로는 100%의 성장률을 가지고 1회 연속 성장할 때 얻게되는 성장량을 의미한다.
위 문장에서 bold처리를 한 두 가지 단어가 핵심이라고 할 수 있다.
100% 성장률로 1회 연속 성장한다는 것의 의미
마법의 저금통이 있다고 상상해보자. 이 저금통은 1원을 넣으면 정확히 1년 뒤에 1원이 더 늘어나(즉, 100% 성장률) 2원이 된다고 하자. 이것을 1회 성장한 것이라고 상정할 수 있다.
이것을 그림으로 표현하면 다음과 같다.
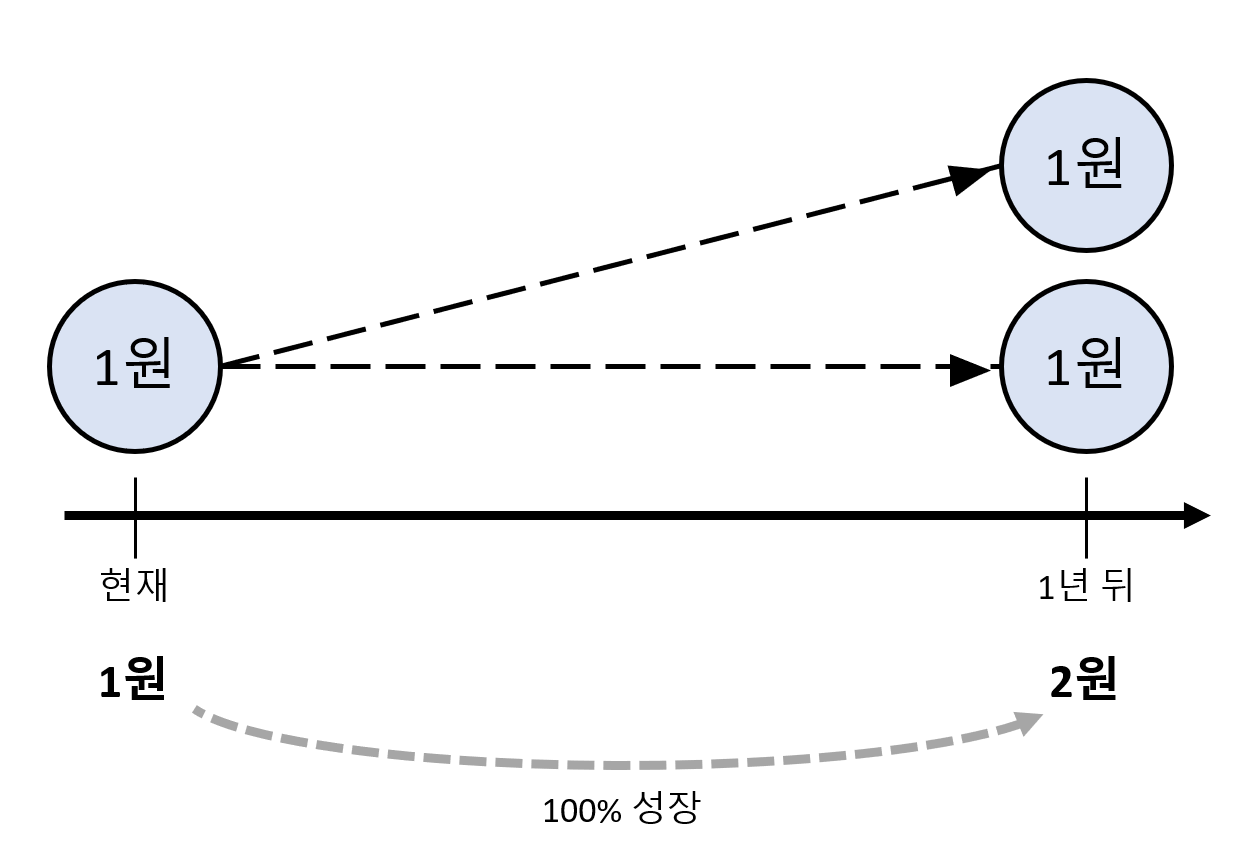
그림 1. 1년 뒤 100% 성장하는 마법의 저금통
그런데, 여기서 만약 6개월마다 50%씩 성장한다고 세팅을 변경하면 어떻게 될까?
1원은 6개월 뒤에 0.5원이 붙고… 그 0.5원도 또 … 말로 설명하면 복잡하니 그림으로 표현하면 아래의 그림 2와 같다.
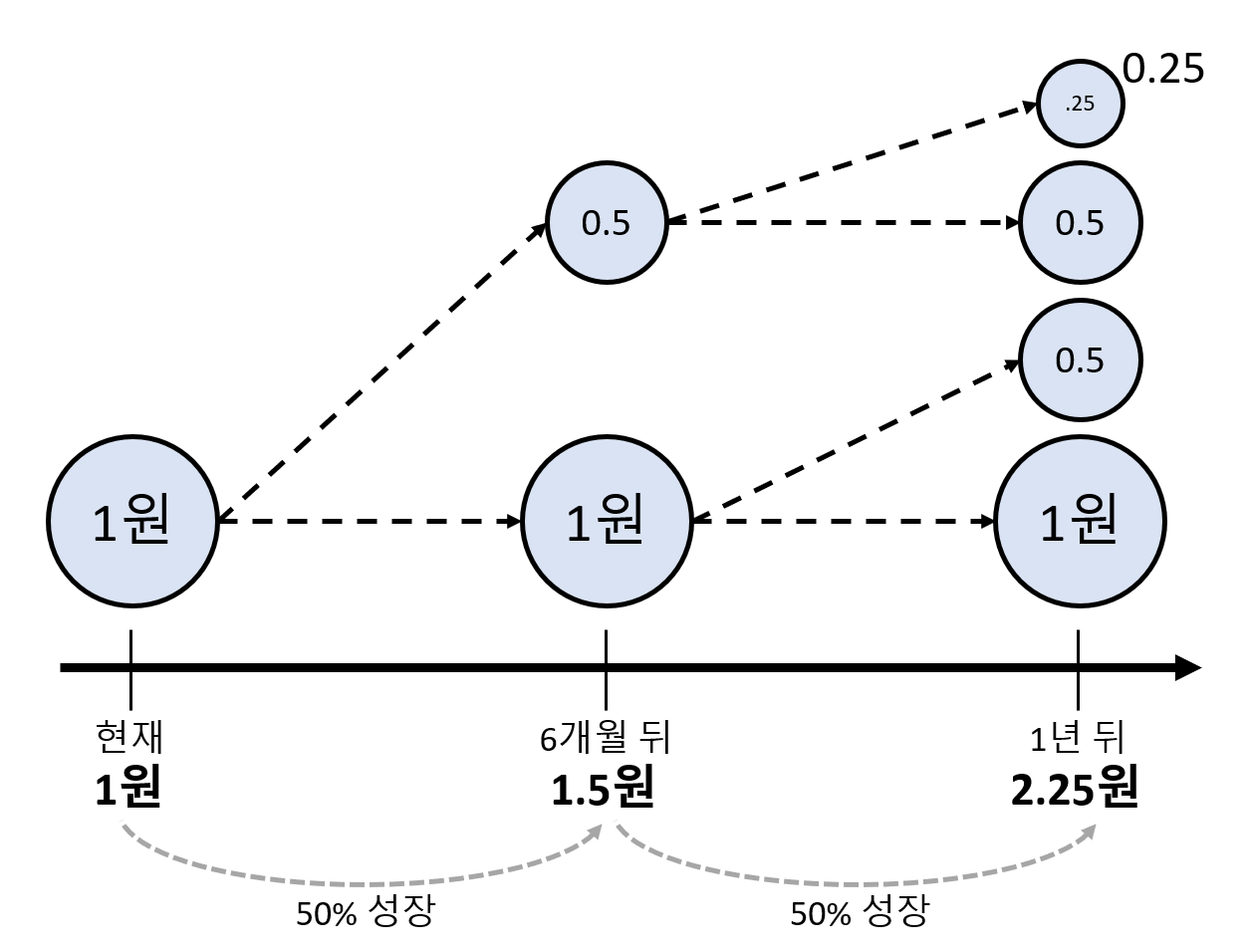
그림 2. 6개월에 50%씩 성장하는 마법의 저금통
여기서, 핵심적인 포인트는 그림 2처럼 6개월 단위로 50%씩 성장시키면 1년 뒤에는 2원이 아니라 2.25원이 된다는 점이다.
즉, 그림 1에서 처럼 한번에 100% 성장 시키는 것 보다 0.25원이나 더 늘었다.
그러면, 3번에 나눠서 성장시킨다면 어떻게 될지 확인해보자.
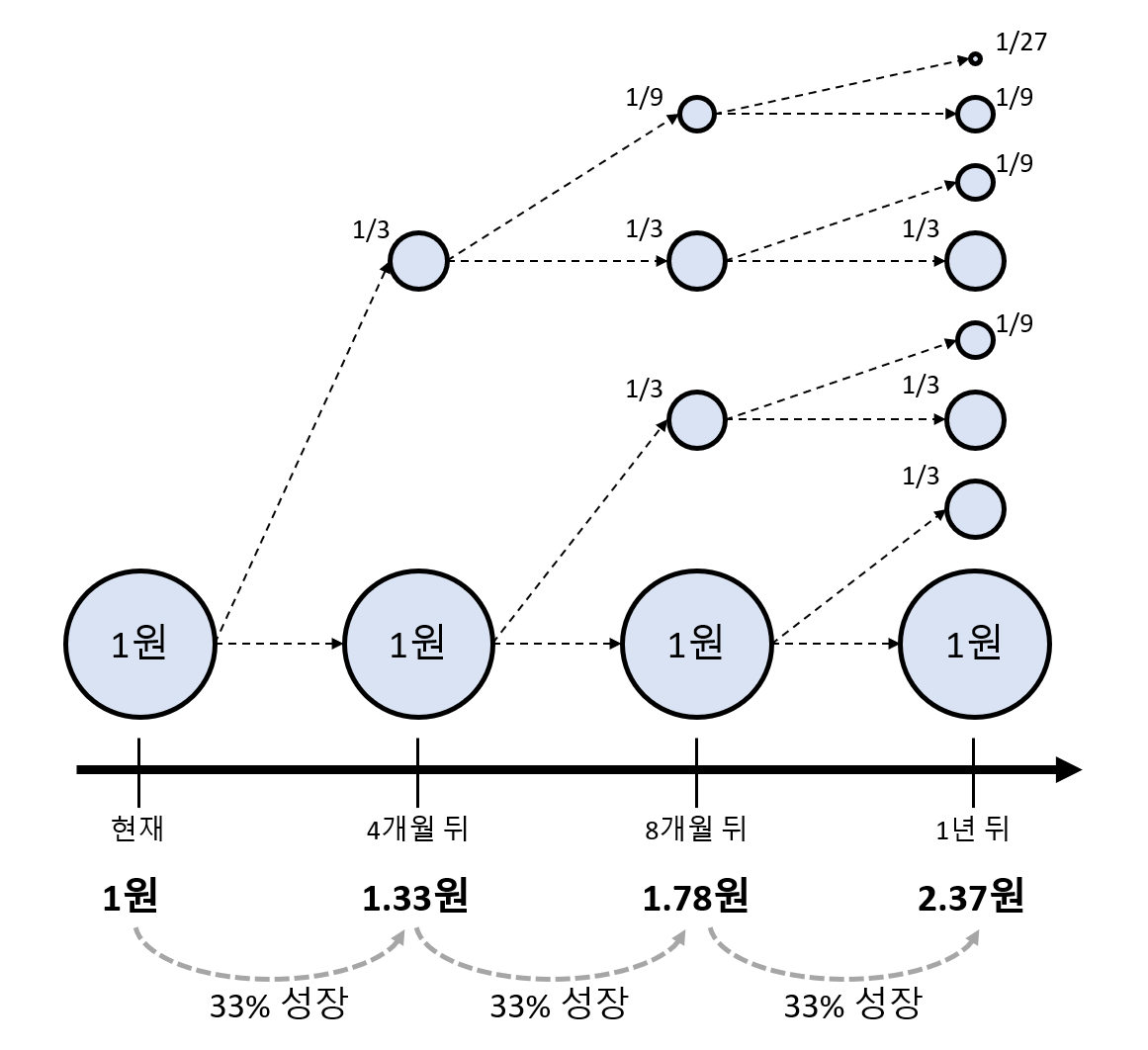
그림 3. 4개월에 33.33%씩 성장하는 마법의 저금통
역시나 6개월에 50% 성장하는 것 보다 4개월에 33.33% 성장하는게 더 성장량이 크다.
그렇다면, 자연스럽게 이런 의문이 들 것이다.
“무한히 많이 쪼개면 어떻게 될까? 성장량도 무한하게 커질까?”
이 의문을 해소하기 위해서는 위의 그림 1, 2, 3의 내용을 수식으로 만들어볼 필요가 있다.
그림 1의 내용을 수식으로 만들면 다음과 같다.
\[1+1 = 2\]그림 2의 내용을 수식으로 만들면 다음과 같다.
\[(1+0.5)\times (1+0.5)\]그림 2가 식 (4)와 같이 쓸 수 있는 이유를 설명하면 다음과 같다.
식 (4)를 풀어쓰면 다음과 같은데,
\[식(4) = 1\times(1+0.5) + 0.5\times(1+0.5)\]즉, 그림 2에서 볼 수 있는 원래의 1원이 1.5원이 되는 과정이 우변의 첫번째 항, 6개월 뒤에 얻어진 0.5원이 0.75원이 되는 과정이 우변의 두 번째 항에서 표현된 것이다.
같은 원리로 그림 3을 수식으로 만들면 다음과 같다.
\[(1+\frac{1}{3})^3\]같은 원리를 이용하여 100% 성장을 n번으로 나눠서 성장시키면 다음과 같은 결과를 얻을 수 있다.
\[(1+\frac{1}{n})^n\]그러면, 무한히 쪼갠다면 아래와 같은 수식으로 그 성장량을 생각할 수 있게 된다.
\[\lim_{n\rightarrow \infty}(1+\frac{1}{n})^n\]잘 알고있듯이 식 (8)이 자연상수 $e$로 정의되는 숫자이며, 그 값은 2.718 가량이다.
여기서 무한히 쪼개서 성장시킨다는 개념을 앞서 언급한 ‘연속 성장’과 맞춰서 생각할 수 있다.
성장 횟수와 성장률에 관하여
앞서 자연상수 $e$는 100%의 성장률을 가지고 1회 연속 성장할 때 얻게되는 성장량을 의미한다고 얘기했다. 또, 100% 성장률로 1회 연속 성장할 때 $e$만큼 성장량을 갖게 된다는 것을 알수 있었다.
그렇다면, 만약 50% 성장률을 가지고 1회 연속성장한다면 그 값은 어떻게 될까?
수식으로 적으면 다음과 같을 것이다.
\[\lim_{n\rightarrow \infty}\left(1+\frac{50\%}{n}\right)^n\] \[=\lim_{n\rightarrow \infty}\left(1+\frac{1}{2n}\right)^n\] \[=\lim_{n\rightarrow \infty}\left(1+\frac{1}{2n}\right)^{2n/2}\] \[=e^{1/2}\]또, 100% 성장률로 2회 연속 성장한다면 그 성장량은
\[e\times e = e^2\]일 것이다.
다시 말해, $e^x$라는 식에서 지수 $x$가 갖는 의미는
\[e^{\text{성쟝횟수 x 성장률}}\]인 것이다.
자연 로그의 의미에 대해서
앞서 $e^x$라는 식에서 지수 $x$가 갖는 의미가 성장횟수와 성장률을 곱한 것과 관련이 되어 있다고 언급했다.
이를 수학적으로 표현하면 자연로그의 의미 중 하나를 쉽게 유추할 수 있다.
즉, 어떤 성장량을 알고 있을 때 성장횟수와 성장률을 곱한 값을 역으로 계산해낼 수 있게 되는 수학적 기술인 것이다.
즉, A라는 성장량을 알고 있다고 하고, 이것을 $A = e^{\text{성장횟수 x 성장률}}$로 나타낼 수 있다고 하면 자연로그를 이용해 아래와 같이 성장횟수 x 성장률을 계산할 수 있다.
\[\ln(e^{\text{성장횟수 x 성장률}}) = \text{성장횟수 x 성장률}\]자연상수가 밑인 지수함수의 미분
고등학교 시절에 배우는 미분에서는 자연상수 $e$를 밑(base)으로 하는 지수함수의 미분에 대해 배우게 된다.
이 부분에 있어 가장 중요한 포인트는 자연상수 $e$를 밑으로 하는 지수함수의 미분은 그 자신이라는 것이다.
다시 말해,
\[\frac{d}{dx}e^x = e^x\]이다.
마치 각도법 대신 호도법을 쓰면 삼각함수의 미분이 깔끔해지는 것 처럼
지수함수에 대해 미분할 때에도 밑이 $e$를 쓰면 미분의 결과가 깔끔해지는 것이다.
만약 밑이 $e$가 아닌 양의 실수라면 어떻게 결과가 바뀌었더라?
공식을 써보면 아래와 같았다.
\[\frac{d}{dx}a^x = a^x \ln(a)\]그래서 미분적분학에서 가능한 많은 지수함수의 밑을 모두 자연상수 $e$로 생각해서 쓰고자 하는 것이다.
다시, 우리의 원래 관심사인 자연상수가 밑인 지수함수의 미분에 대해 돌아와보자.
우리는 식 (16)의 의미를 어떻게 받아들여야 할까?
그것은
- 식 (16)이 정말 연속성장을 의미하는가?
라는 점과
- 식 (16)에서 지수함수의 밑이 $e$여야 하는가라는 점이다.
식 (16)에서 $y=e^x$가 아니라 임의의 함수 $y$라고 써보자. 그러면 미분방정식이 보인다.
\[\frac{dy}{dx}=y\]식 (18)의 의미가 뭘까? 이게 왜 성장과 관련이 있는 것일까?
이를 알아보기 위해 미분의 원래 공식을 다시 써보도록 하자.
$y=f(x)$라고 하면,
\[식 (18) = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}=f(x)\]이렇게까지 썼지만 식 (19)에서 갖는 극한이 어려워 보이기 때문에 $h=1$인 경우부터 차근히 생각해보자.
1. 식 (16)이 정말 연속 성장을 의미하는가?
1) $h=1$인 경우
식 (16)의 의미를 조금 더 깊이 생각하기 위해 식 (19)를 가져와 $h$의 값을 점점 작게 만들어보자.
\[식(19)\Rightarrow \frac{f(x+1)-f(x)}{1} = f(x)\] \[\Rightarrow f(x+1) = 2f(x)\]식 (21)이 말하는 것은 뭔가? 바로 $f(x) = 2^x$라는 뜻이다. 그림으로 그리면 다음과 같다.
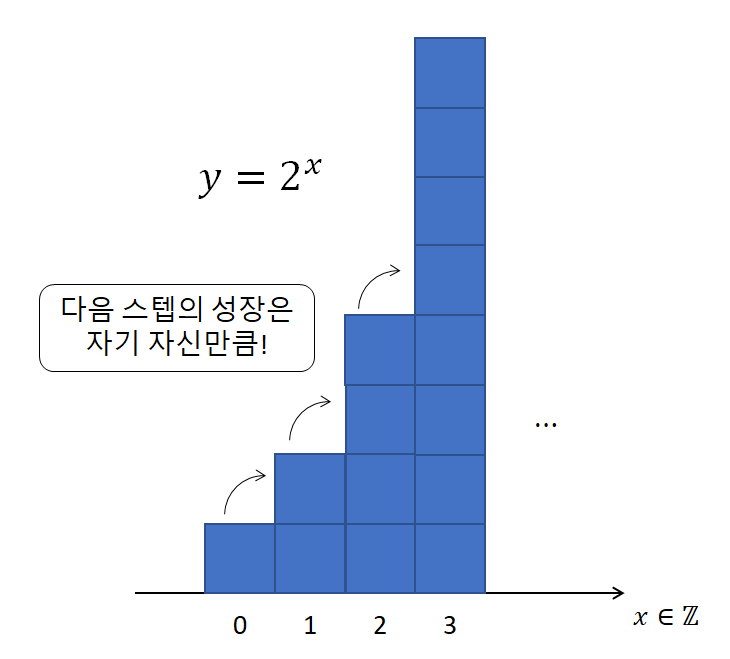
그림 4. $f=2^x$에서 매 $x$의 성장률은 자기 자신이다.
즉, $h=1$일 때 식 (18)의 의미를 조금 자세히 볼 수 있다. 변화율이 자기 자신이라는 것이다.
다시 말해 다음번 $x$에서는 지금의 함수 크기만큼 키워준다는 뜻이기도 하다.
2) $h=0.5$인 경우
이번에는 식 (19)에 대해 $h=0.5$인 경우에 대해 생각해보자.
\[식(19) \Rightarrow \frac{f(x+0.5)-f(x)}{0.5}=f(x)\] \[\Rightarrow f(x+0.5) = 1.5 f(x)\]이런 식으로 $h$가 매우 작은 경우에 대해서도 생각해볼 수 있을 것이다.
3) $h=0.00001$인 경우
\[식(19)\Rightarrow \frac{f(x+0.00001)- f(x)}{0.00001}=f(x)\] \[\Rightarrow f(x+0.00001) = 1.00001f(x)\]식 (25)가 말하는 것은 무엇인가? 그것은 바로
라는 것이다.
다시 말해 매번 아주 작은 스텝에서 매우 조금씩 크게 만들겠다는 것이고 이것은 다시 말하면 연속 성장이다.
2. 식 (16)에서 지수함수의 밑이 $e$여야 하는가
식 (18)을 다시 써보자.
\[\frac{dy}{dx}=y \notag\]식 (18)의 미분방정식을 풀기 위해 y는 모두 좌변으로, x는 모두 우변으로 옮기면 다음과 같다.
\[\Rightarrow \frac{1}{y}dy = dx\]이 때 양변에 모두 적분을 취해주자.
\[\Rightarrow \int \frac{1}{y}dy = \int dx\]여기서 $\ln(y)$의 정의가 바로 $\int\frac{1}{y}dy$이므로 좌변의 값은 $\ln(y)$와 같다.
이것의 증명은 아래와 같이 $\ln(x)$의 미분이 $1/x$임을 보임으로써 확인할 수 있다.
다시 말해,
\[\frac{d}{dx}\ln(x) = \frac{1}{x}\]이므로 미적분학의 기본정리에 의해,
\[\int \frac{1}{x}dx = \ln(x)+C\] \[\text{여기서 }C\text{는 적분상수}\notag\]임을 알 수 있는 것이다.
이를 확인해보자면,
\[\frac{d}{dx}\ln(x) = \lim_{h\rightarrow 0}\frac{\ln(x+h)-\ln(x)}{h}\] \[=\lim_{h\rightarrow 0}\frac{\ln\left(\frac{x+h}{x}\right)}{h}\] \[=\lim_{h\rightarrow 0}\ln\left(\frac{x+h}{x}\right)^{\frac{1}{h}}\] \[=\lim_{h\rightarrow 0}\ln\left(1+\frac{h}{x}\right)^{\frac{x}{h}\cdot\frac{1}{x}}\] \[=\ln(e^{\frac{1}{x}})=\frac{1}{x}\]따라서 식 (27)은 다음과 같이 쓸 수 있다.
\[\Rightarrow \ln(y) = x\]그러므로
\[y=e^x\]이다.
즉, 식 (18)에서의 함수는 지수함수이면서 밑은 $e$인 지수함수이다.