Prerequisites
본 포스팅의 내용에 대해 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
회귀에서 분류로…
선형회귀 (최적화 관점) 편에서 확인한 데이터들은 라벨 값(즉, 아래의 그림 1에서 사고 발생 건수)이 연속적인 것이었다.
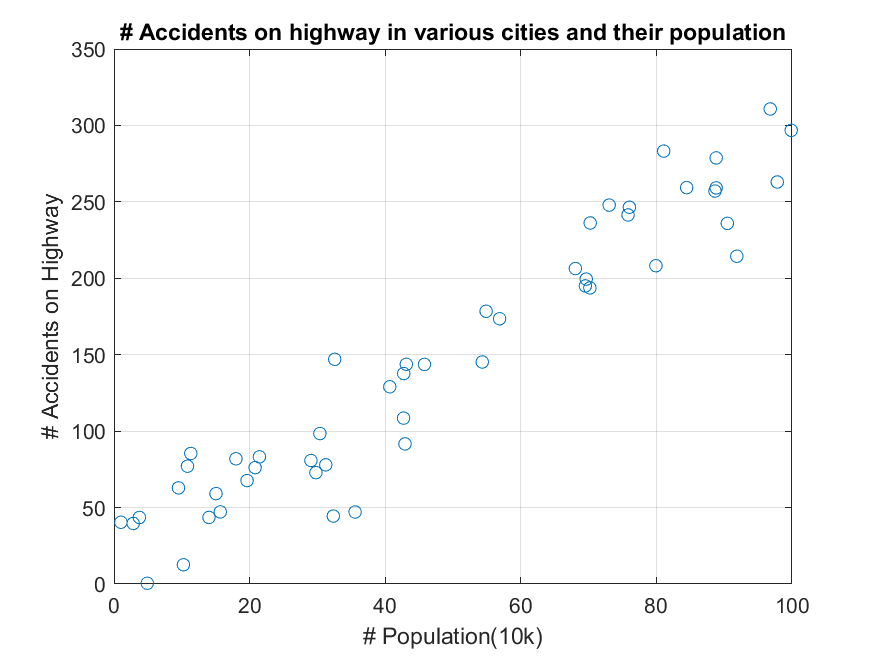
그림 1. 선형회귀 모델 구축 시 이용한 연속적 라벨을 가지는 데이터
하지만 어떤 경우에는 다음과 같이 라벨이 범주형일 수도 있다. 라벨이 범주형이라는 것은 가령 “남자, 여자” 혹은 “강아지, 고양이” 등의 연속적인 숫자로 나타내기 어려운 데이터들을 얘기하고 보통 0 혹은 1로 숫자로 치환해 생각한다.
가령 아래와 같이 $x$라는 특성값이 5보다 작으면 클래스가 0으로, 5보다 같거나 크면 클래스가 1로 결정된다고 생각해보자.
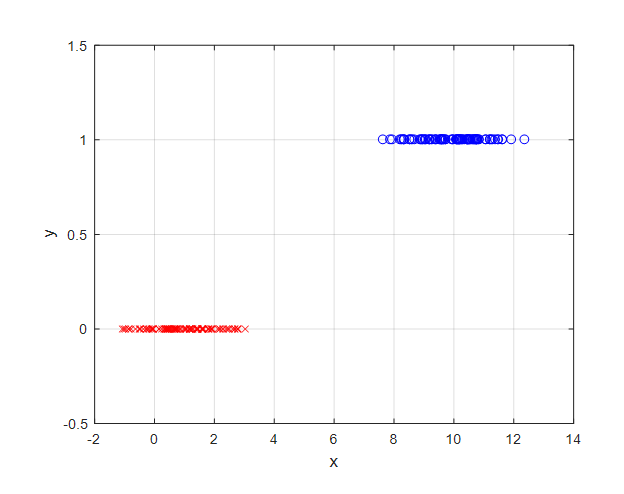
그림 2. 범주형 데이터의 예시. 특성값 $x$가 5보다 작으면 클래스 0, 5보다 크거나 같으면 클래스 1로 분류할 수 있다고 하자.
그런데 만약 이렇듯이 범주형 라벨을 가지는 데이터에 대해 선형회귀 메소드를 적용하면 다음과 같은 결과를 얻을 것이다.
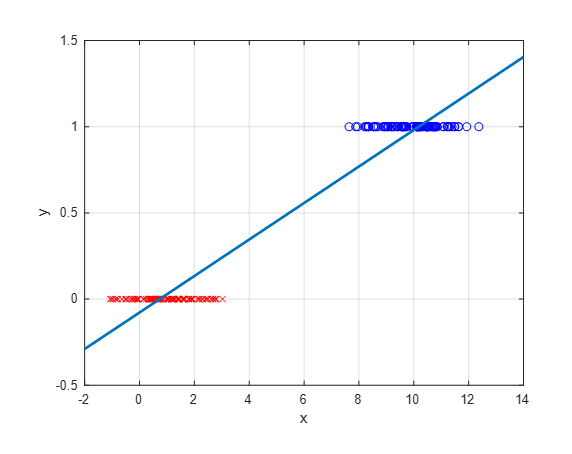
그림 3. 범주형 데이터에 대해 선형회귀 모델을 적용하는 경우
선형회귀 메소드를 적용했을 때에도 $\hat{y} = ax+b\geq 0.5$인 경우 1로 분류하고 아닌 경우 0으로 분류할 수 있다.
하지만, 범주형 데이터에 대해 회귀분석을 한다고 하면 다음과 같은 함수를 이용하는게 더 좋은 결과를 얻을 수 있을 것이다.
다시 말해, 선형 모델모다 범주형 데이터에 좀 더 어울리는 모델을 생각해보도록 하자.
범주형 데이터에 대한 모델을 세우기 위해서 필요한 함수는 아래의 그림 4와 같이 어떤 값을 넘어가기 전에는 0, 넘어간 뒤에는 1의 값을 가지는 형태의 함수여야 한다.
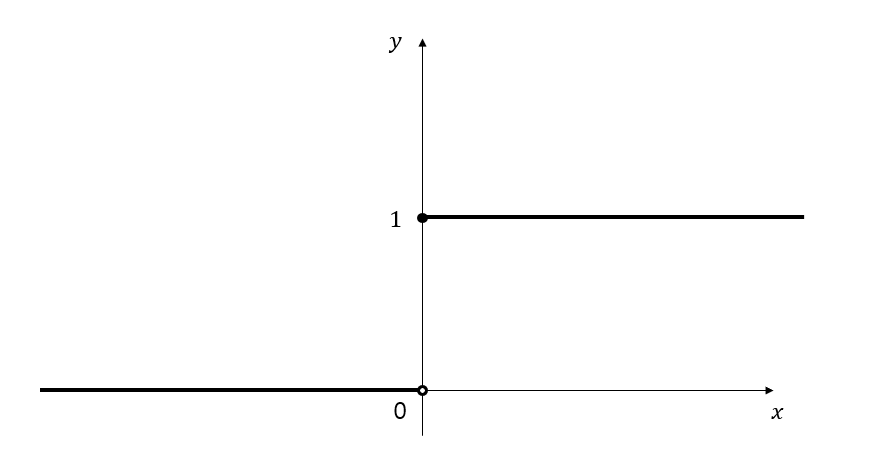
그림 4. 범주형 데이터에 어울리는 함수의 형태는 특정 $x$값 이전에는 0을 출력하고 그 값 이후에는 1을 출력해주는 커브여야 한다.
이 S자 커브 함수에 대한 여러가지 후보가 있겠으나 우리는 sigmoid 함수를 사용하도록 하자.
sigmoid 함수는 다음과 같이 쓴다.
\[S(x) = \frac{1}{1+\exp(-x)}\]sigmoid함수 외에도 다른 함수를 쓸 수 있지만 굳이 sigmoid 함수를 쓰는 이유는 독립변수 $x$들의 각 클래스에 대한 분포가 정규분포를 따를 것으로 가정하기 때문인데 이에 대해선 추후에 다뤄보도록 하자.
어찌되었건 sigmoid 함수의 형태는 아래와 같다.
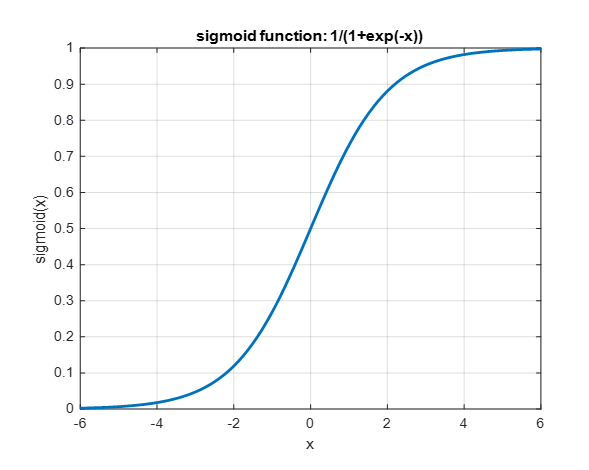
그림 5. sigmoid 함수의 형태
이 sigmoid 함수의 출력이 0.5보다 큰 경우에는 label을 1로 생각하고, 그렇지 않은 경우에는 label을 0으로 생각할 수 있다.
그림 2에서 확인한 우리의 데이터에 sigmoid 함수를 적용하면 아래의 그림 6과 같은 형태일 것이다.
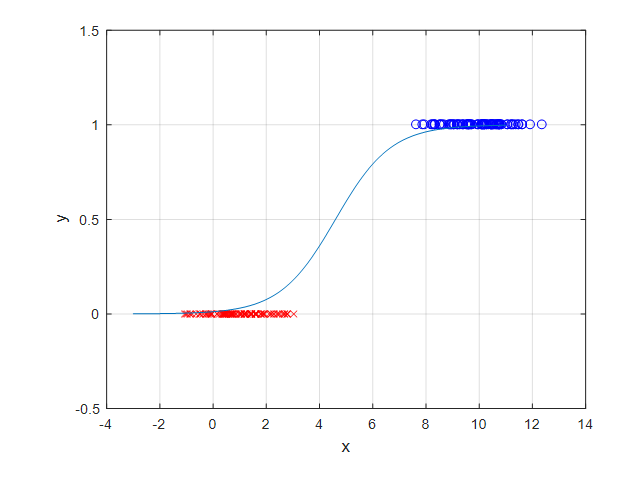
그림 6. Sigmoid 함수를 이용해 회귀모델을 만든 경우의 예시
이 때, 우리가 sigmoid 함수의 형태를 결정하기 위해서 다음과 같이 파라미터 $a$와 $b$를 sigmoid 함수의 식에 넣어주도록 하자.
\[S(x) = \frac{1}{\exp(-(ax+b))}\]이 형태를 잘 생각해보면 $ax+b$를 특정 함수에 넣은 꼴이라고도 볼 수 있을 것 같다.
$b$의 값은 sigmoid 함수를 좌우로 움직여주는 역할을 할 것이고 $a$값은 sigmoid 함수의 가파른 정도를 결정할 것이다.
슬라이더를 움직여 보세요 ^^
어찌되었건 우리가 정해야 하는 $a$와 $b$ 값이며 선형회귀를 이용한 모델 구축 시와 마찬가지로 Error를 정의하고 이 Error를 최소화하는 방식으로 $a$와 $b$를 정할 수 있을 것이다.
Error 함수 정의
우리는 이제 model을 결정하였기 때문에 Error를 정의하고 이를 최소화함으로써 파라미터를 결정할 수 있다.
우리가 지금 생각하고 있는 문제는 binary classification인데, 출력은 0 혹은 1로 정해져 있다.
생각해보면 선형 회귀에서 다루었던 회귀모델과는 약간의 차이가 있는데 분류 문제의 경우에는 정답이 맞거나 틀리거나 둘 중 하나라는 점이다.
따라서, 우리는 정답을 맞추었을때는 Error 값을 0으로, 정답을 맞추지 못했을 때는 Error값을 가능한 크게 줄 수 있도록 하자.
우리의 식 (2)에서 얻게되는 결과 값을 $P$라고 이름 붙이자. 굳이 $P$라고 이름 붙이는 것은 라벨에 대한 확률값을 출력해준다고 볼 수 있기 때문이다. 가령 $P$값이 0.5보다 크거나 같으면 이 데이터에 대한 라벨을 1로 예측하고, 그렇지 못하면 라벨을 0으로 예측할 것이기 때문이다.
즉, 우리 모델의 출력함수는 다음과 같다.
\[P = \frac{1}{1+\exp(-(ax+b))}\]즉, 우리가 원하는 것은 원래의 라벨 $y$가 $1$일 때 $P$의 값이 0이면 에러 값을 크게 주고, 또, 라벨 $y$가 $0$일 때 $P$의 값이 1이면 에러 값을 크게 주는 것이다.
이것을 로그함수를 이용해 쓸 수 있는데, 로그 함수의 형태를 생각하면
\[\begin{cases} \lim_{x\rightarrow 0^+}\log(x) = -\infty \\ \log(1) = 0\end{cases}\]이기 때문에 이를 이용하자는 것이다.
즉, 우리의 에러는 다음과 같이 생각할 수 있다.
\[E(y, P) = \begin{cases}-\log(P) &&\text{ if } y = 1 \\ -\log(1-P) &&\text{ if }y = 0\end{cases}\]위의 식 (5)를 잘 생각해보면 $y=1$ 일 때는 $P$가 0으로 출력되면 무한대 값이 출력되지만 $P$가 1로 출력되면 Error는 0이다.
또, 반대로 $y=0$일 때는 $P$가 $0$으로 출력되면 $-\log(1-P)$는 $\log(1)$은 0이지만 $P$가 1로 출력되면 Error는 무한대이다.
classification이라는 특성 상 $y$는 $0$ 또는 $1$의 값만 가지므로 식 (5)는 아래와 같이 한줄로 쓸 수도 있다.
\[E(y, P) = -(y\log(P)+(1-y)\log(1-P))\]Error에 대한 gradient 계산
P에 대한 편미분 계산
계산의 편의를 위해 다음과 같이 변수들을 벡터화 시키도록 하자.
\[X=\begin{bmatrix}x \\ 1\end{bmatrix}\] \[\theta = \begin{bmatrix}a\\b\end{bmatrix}\]따라서, $ax+b$는 다음과 같이 쓸 수 있다.
\[\theta^TX=\begin{bmatrix}a & b\end{bmatrix}\begin{bmatrix}x \\ 1\end{bmatrix}\]먼저, $P(X,\theta) = 1/(1+\exp(-\theta^T X))$라고 하면,
\[\frac{\partial P}{\partial \theta} = \frac{\partial}{\partial \theta}\left(\frac{1}{1+\exp(-\theta^TX)}\right)\]분자식의 형태로 되어있는 함수에 대한 미분을 적용하면,
\[\Rightarrow\frac{(-1)(1+\exp(-\theta^T X))'}{(1+\exp(-\theta^TX))^2}\]여기서 $1+\exp(-\theta^TX)$를 $\theta$에 대해 미분해주자.
\[\Rightarrow\frac{(-1)(\exp(-\theta^TX))(-X)}{(1+\exp(-\theta^TX))^2}\]이제 부호를 정리해주면 아래와 같다.
\[\Rightarrow \frac{\exp(-\theta^TX)X}{(1+\exp(-\theta^TX))^2}\]여기서 분모의 제곱항을 다시 나눠 쓰면 다음과 같다.
\[\Rightarrow\frac{\exp(-\theta^TX)X}{(1+\exp(-\theta^TX))(1+\exp(-\theta^TX))}\]따라서 또 나눠 쓰면 다음과 같이도 쓸 수 있을 것이다.
\[\Rightarrow \left(\frac{1}{1+\exp(-\theta^TX)}\right)\left(\frac{\exp(-\theta^TX)}{1+\exp(-\theta^TX)}\right)X\]여기서 두 번째 term은 1을 더하고 1을 빼도 결과는 변화가 없으므로,
\[=\left(\frac{1}{1+\exp(-\theta^TX)}\right)\left(\frac{1+\exp(-\theta^TX)-1}{1+\exp(-\theta^TX)}\right)X\]즉, 원래의 $P(X, \theta)$에 대한 정의를 이용하여 다음과 같이 쓸 수 있다.
\[= P(X,\theta)(1-P(X,\theta))X\]Error에 대한 편미분 계산
우리는 error를 다음과 같이 정의하였다.
\[E(y, P) = -(y\log(P)+(1-y)\log(1-P))\]이제 이를 $\theta$에 대해 편미분 해주도록 하자.
\[\frac{\partial E}{\partial \theta}=-\left(y\frac{\partial \log(P)}{\partial \theta}+(1-y)\frac{\partial\log(1-P)}{\partial \theta}\right)\]chain rule을 이용해 위 식 (19)는 다음과 같이 쓸 수 있다.
\[\Rightarrow -\left(y\frac{\partial \log(P)}{\partial P}\frac{\partial P}{\partial \theta}+(1-y)\frac{\partial \log(1-P)}{\partial (1-P)}\frac{\partial(1-P)}{\partial P}\frac{\partial P}{\partial \theta}\right)\]자연로그 $\log(x)$를 $x$에 대해 편미분하면 $1/x$이므로 다음과 같이 쓸 수 있다.
\[\Rightarrow -\left(y\frac{1}{P}\frac{\partial P}{\partial \theta}+(1-y)\frac{1}{1-P}(-1)\frac{\partial P}{\partial \theta}\right)\]여기서 부호를 조금 정리해주면,
\[\Rightarrow -y\frac{1}{P}\frac{\partial P}{\partial \theta}+(1-y)\frac{1}{1-P}\frac{\partial P}{\partial \theta}\]이제 $\partial P /\partial \theta$는 식 (17)을 이용해 다음과 같이 써줄 수 있게 된다.
\[\Rightarrow -y\frac{1}{P}P(1-P)X+(1-y)\frac{1}{1-P}P(1-P)X\]위 식을 약분해서 조금 정리하면 다음과 같다.
\[\Rightarrow -y(1-P)X + (1-y)PX\] \[=-Xy+PXy+PX-PXy\] \[=(P-y)X\]즉,
\[\frac{\partial E}{\partial \theta} = (P-y)X\]이다.
이제 $\theta$는 a와 b에 대해 말해주고 있는 것이므로, 우리의 파라미터 $a$와 $b$에 대한 편미분은 각각 다음과 같이 생각할 수 있는 것이다.
\[\therefore \frac{\partial E}{\partial a}=(P-y)x\]이고,
\[\frac{\partial E}{\partial b}=(P-y)\]이다.
회귀 모델 구축 결과
이제 선형회귀에서와 마찬가지로 gradient descent를 이용해 최적의 $a$와 $b$를 구하면 우리의 데이터에 대한 적절한 sigmoid 함수의 형태와 위치를 얻을 수 있다.
gradient descent를 이용한 logistic regression을 구현한 MATLAB 코드는 아래의 위치에서 다운 받을 수 있다.