행렬이 positive definite 이기 위한 조건은 무엇일까?
Prerequisites
양의 정부호 행렬에 대해 더 잘 알기 위해서는 아래의 내용에 대해 알고 오시는 것이 좋습니다.
정의(Definition)
우선 양의 정부호 (positive definite) 행렬의 정의부터 차근히 살펴보도록 하자.
영벡터가 아닌 임의의 열벡터 $x$와 대칭 행렬 $A$에 대해 다음이 성립한다면 $A$는 양의 정부호(positive definite) 행렬이다.
\[x^TAx >0\]생각해보면 굉장히 이상한 정의다. 행렬에 대해 정의하는데 왜 열벡터 $x$를 한쪽에는 전치(transpose)를 취하고 다른 한쪽에는 취하지 않고 곱한다는 것일까?
양의 정부호 행렬의 의미
양의 정부호라는 이름이 갖는 의미
수학 용어들 중 번역이 굉장히 잘 된 용어들이 있다. 양의 정부호라는 번역도 positive definite이라는 영어 단어에 비해서 그 의미가 더 잘 와닿게 번역된 것 같다.
양의 정부호는 부호와 관련이 있다. 다시 말해 행렬이 양의 정부호 행렬이라면 양수가 작동하는 방식이 그대로 적용되어 작동하는 것과 유사함을 시사한다.
임의의 양의 실수 $a$를 생각해보자. 또, 임의의 실수 $b$도 생각해보자.
$a$가 양수이면, $b$에 곱했을 때 그 부호가 그대로 유지된다는 것은 아주 기초적인 결과이다.
다시 말해, $a$가 양수이면 $b$에 곱했을 때 $b$의 크기는 키워주지만 방향을 뒤집어주지는 않는다.
이번엔 임의의 벡터 $a$, $b$를 생각해보자. 그리고 이 두 벡터에 대한 내적을 생각해보자. 일반적으로 정의하는 내적은 다음과 같이 계산된다.
\[a^Tb = |a||b|\cos(\theta)\]여기서 $\theta$는 $a$와 $b$의 사잇각이다. 그리고 $-\pi/2 \lt \theta \lt \pi/2$라는 조건을 만족할 때 $a^Tb > 0$이다.
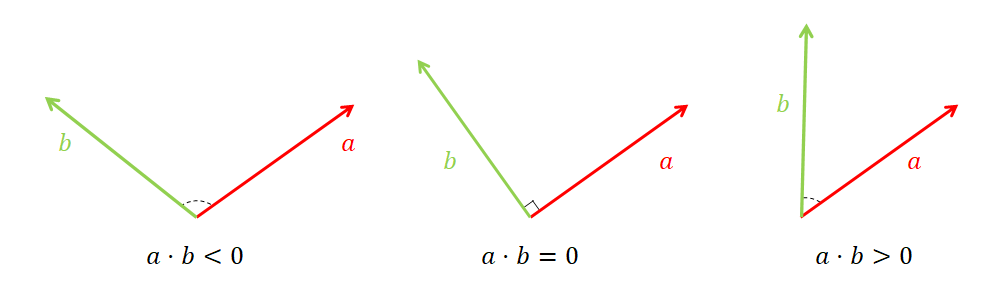
그림 1. 두 벡터를 내적 시 두 벡터 간의 사잇각이 예각인 경우 내적값은 양수, 둔각인 경우는 내적값은 음수가 된다.
이제 양의 정부호 행렬의 정의를 생각해보면, 영벡터가 아닌 열벡터 $x$에 대해 다음을 만족해야 임의의 대칭 행렬 $A$가 양의 정부호 행렬이다.
\[x^TAx>0\]여기서 $x^TAx$를 괄호를 이용해 다음과 같이 써보자.
\[x^TAx \rightarrow x^T(Ax)\]즉, 위 식은 임의의 영벡터가 아닌 벡터 $x$에 대해 선형 변환 $A$를 취해준 다음 원래의 $x$와 내적을 취해준 것으로 해석할 수도 있다.
앞서 말했던 것 처럼 두 벡터를 내적해서 양의 값이 나오기 위해서는 두 벡터 간의 사잇각이 $-\pi/2 \lt \theta \lt \pi/2$을 만족해야 한다.
그러므로, 결국 $x$에 선형 변환을 시켜줬을 때 변환 전 후의 각도 변화가 -90도에서 90도 사이에서 변하게 된다는 뜻으로 볼 수 있다.
즉, 양의 실수처럼 양의 정부호 행렬을 이용한 선형변환은 입력 벡터를 ‘뒤집어주지는 않는’ 것이어야 한다.
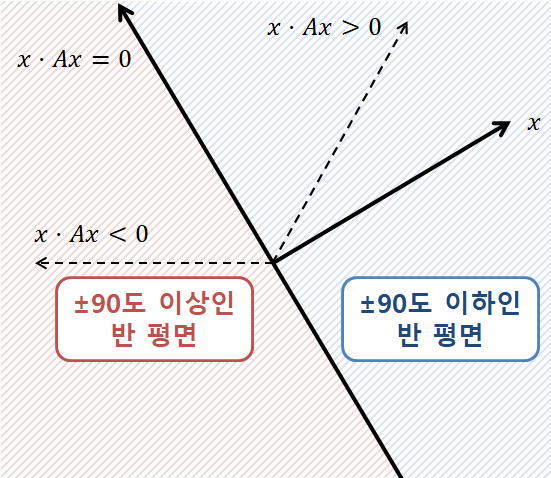
그림 2. 양의 정부호 행렬은 선형변환 시 변환 전 후의 각도 변화가 -90도에서 90도 사이에서만 변화하게 된다. (즉, 변환 후에도 파란색 영역에 들어오게 한다.)
양의 정부호와 고윳값
양의 정부호 행렬의 정의에 따르는 성질이지만 양의 정부호 행렬과 고윳값의 부호는 연관성이 깊다.
\[Ax=\lambda x\] \[x^TAx = x^T\lambda x=\lambda |x|^2\]이 때, 정의상 $x^TAx >0 $ 이므로 $\lambda>0$이다.
다시 말해 행렬 $A$가 대칭행렬이라는 조건 하에 고윳값의 부호가 모두 양수라는 조건은 행렬 $A$가 양의 정부호 행렬임을 말해주는 조건이다.
그런데, 고윳값의 의미를 다시 한번 생각해보면 고윳값은 행렬이 가져다주는 선형변환에 대한 방향성을 의미해준다.
고윳값은 고유벡터의 방향으로 얼마만큼 행렬이 변하는지를 보여주는데, 고윳값이 양수라는 말은 그 방향으로 scaling 되어서 커지거나 작아지는 변환을 수행하지만 뒤집어지지 않는 변환임을 얘기해준다.
이 포스팅의 가장 위에 있는 Javascript Applet을 이용해 좀 더 생각해보자.
빨간 화살표 끝에 있는 동그라미를 클릭하면 선형 변환 후의 기저벡터들을 결정함으로써 원하는 행렬 $A$를 선택할 수 있는데,
빨간 화살표와 초록 화살표가 -90도 ~ 90도 내에서 서로 뒤집히지 않는 경우에는 행렬 $A$는 양의 정부호 행렬인데 반해, 빨간 화살표와 초록 화살표가 이동 범위가 -90도 ~ 90도를 넘어가거나 두 화살표가 뒤집히는 경우에는 양의 정부호 행렬이 아니게 되는 것을 알 수 있다.
그러면서 동시에 고윳값의 변화도 함께 확인해볼 수 있는데, 양의 정부호인 경우, 즉, 화살표들이 서로 뒤집히지 않거나 -90도~90도 내의 변화만 있는 경우에는 고윳값이 모두 양수이고,
그렇지 않은 경우에는 두 고윳값 중 적어도 하나는 음수 고윳값을 갖게되는 것을 알 수 있다.
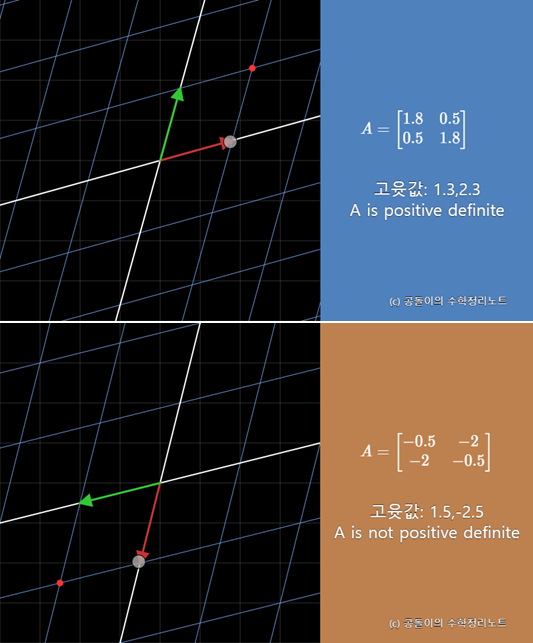
그림 3. 선형 변환 후에 기저벡터들이 서로 뒤집히거나 두 기저벡터 간의 각도가 -90 ~ 90도를 넘어가는 경우 두 고윳값 중 적어도 하나는 음수가 된다.
양의 정부호와 헤시안 행렬
양의 정부호 여부가 가장 중요하게 사용되는 응용 분야 중 하나는 최적화 분야이다.
최적화 이론에서는 함수의 최솟값을 찾는 것을 최종 목표로 한다고 볼 수 있다.
일전에 헤시안 행렬에 대해 다룬 적 있었지만, 헤시안 행렬은 2차 미분계수와 비슷한 의미를 갖는다고도 언급한 바 있다.
어떻게 생각하면 헤시안 행렬은 기본 bowl의 형태를 더 볼록하거나 오목하게 만드는 기하학적인 변환을 수행해주는 역할이라고도 할 수 있는데,
그림으로 보면 다음과 같다.
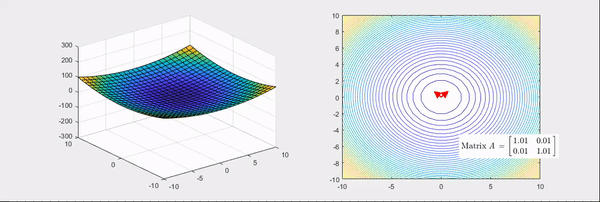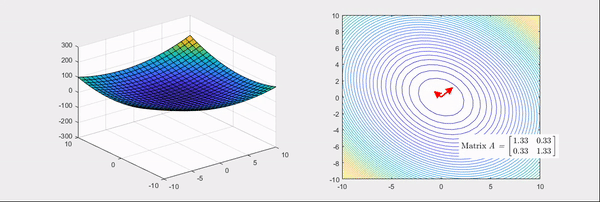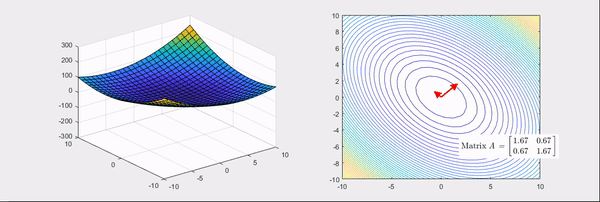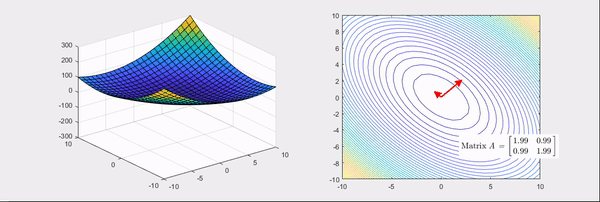
그림 4. 헤시안 행렬의 고윳값이 모두 양수인 경우
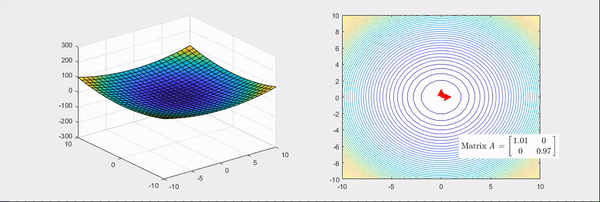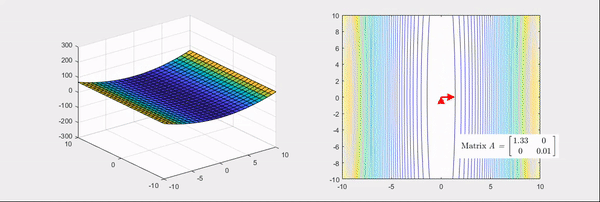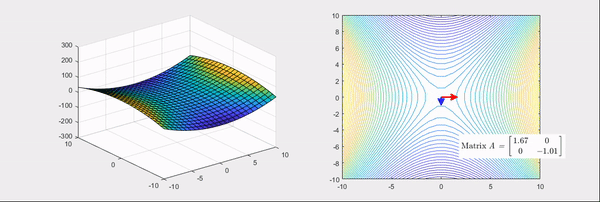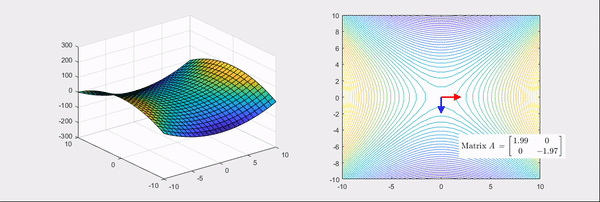
그림 5. 헤시안 행렬의 고윳값이 하나는 양수이고 하나는 음수인 경우
위 그림들의 화살표는 헤시안 행렬의 고유벡터 방향을 나타내고, 빨간색인 경우는 고윳값이 양수, 파란색인 경우는 고윳값이 음수인 경우를 의미한다.
잘 보면 고윳값이 모두 양수인 경우의 헤시안 행렬을 이용한 선형변환은 기본 bowl 형태가 더 볼록하게 만들어지는 것을 알 수 있다.
반면에 두 번째 그림에서 처럼 고윳값이 하나는 양수이지만 나머지 하나는 음수가 되면, 기본 bowl 형태가 안장(saddle) 형태로 바뀌는 것을 볼 수 있다.
즉, 헤시안 행렬은 대칭행렬이고, 거기서 헤시안 행렬에서 고윳값이 모두 양수라는 것은 헤시안 행렬이 양의 정부호 행렬임을 의미한다.
다시 말해, 어떤 두 번 미분가능한 실함수 $f$에 대해 Hessian 행렬이 양의 정부호 행렬이라면 이 함수의 전체적인 형태는 아래로 볼록하고, 필연적으로 극소값을 갖는다는 것을 알 수 있다.
만약 여기서 gradient를 구해서 0인 지점을 찾는다면 그 포인트가 바로 극소값임을 알 수 있다.