pole의 위치와 기저 함수 $\exp(\sigma t)$의 관계
출처: MIT Mathlets, https://mathlets.org/mathlets/poles-and-vibrations/

pole diagram과 주파수 응답의 관계
출처: MIT Mathlets, https://mathlets.org/mathlets/amplitude-response-pole-diagram/

Prerequisites

이번 포스팅을 더 잘 이해하기 위해서는 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 신호 공간(signal space)
• 푸리에 급수(Fourier Series)
• 푸리에 변환(Fourier Transform)

이하의 내용에서 $\delta(t)$는 디랙 델타 함수를 의미합니다.

\[\delta(t) =\begin{cases} \infty, && t = 0 \\ 0 && \text{otherwise}\end{cases}, \quad \int_{-\infty}^{\infty}\delta(t)dt = 1\]

또, $u(t-t_0)$는 unit step function 을 나타냅니다.

\[u(t-t_0)=\begin{cases} 1 && t \geq t_0 \\ 0 && \text{otherwise}\end{cases}\]

푸리에 변환의 한계

앞서 푸리에 급수와 푸리에 변환에 대해 공부하면서 연속 시간 신호에 대한 주파수 해석을 할 수 있게 되었다. 그 뿐만 아니라 푸리에 해석 방법은 LTI system에 아주 유용하게 적용할 수 있어서 시스템의 impulse response에 푸리에 변환을 적용하면 LTI system에 대한 주파수 응답 특성을 이해할 수 있었다.

그런데, 푸리에 급수 혹은 변환을 이용하기 위해선 조건이 붙는다. 일명 디리클레 조건이라고 하는 것인데, 말하자면 변환하고자 하는 신호가 absolutely integrable해야한다는 것이다. 만약 변환하고자 하는 것이 신호라면 발산하지 않는 신호여야 할 것이고 만약 impulse response라면 stable system의 impulse response만 푸리에 분석을 적용할 수 있다는 의미이다.

가령 $x(t) = e^{at}\cos(b t)u(t), \text{ for }a\gt 0$ 같은 신호 혹은 이와 같은 impulse response를 갖는 시스템은 푸리에 변환이 존재하지 않기 때문에 푸리에 해석을 통해 주파수 분석을 수행할 수 없다. 시간이 흘러감에 따라 신호의 크기가 무한대로 발산하기 때문이다

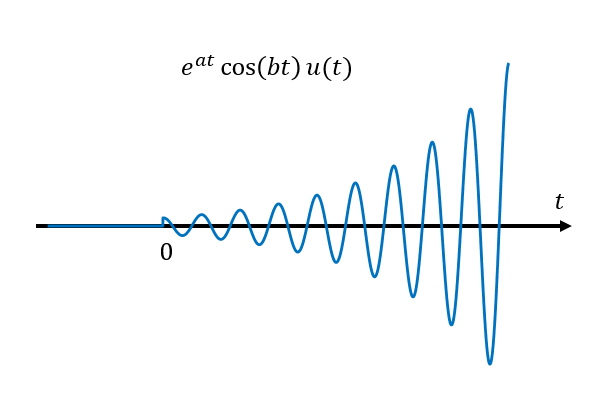
그림 1. 시간이 지남에 따라 발산하는 정현파

하지만 불안정한 시스템도 주파수 분석을 할 수만 있다면 유용한 점이 많을 것이다. 가령, 이 신호 혹은 임펄스 응답이 얼마나 빠른 속도로 발산하게 되는지, 그리고 어떤 주파수로 oscilating하는지 등에 대해 알 수 있게 된다는 것이다.

피에르 시몽 라플라스(Pierre Simon Laplace, 1749-1827)는 이런 한계를 극복할 수 있게 푸리에 변환을 일반화시킬 수 있는 변환을 생각해냈다¹.

라플라스 변환의 아이디어

아이디어는 아주 간단하다. 임의의 실수 $\sigma$를 상정하고 oscilating term을 상쇄시킬 수 있는 적절한 $\exp(-\sigma t)$를 곱해서 푸리에 변환하는 것이다.

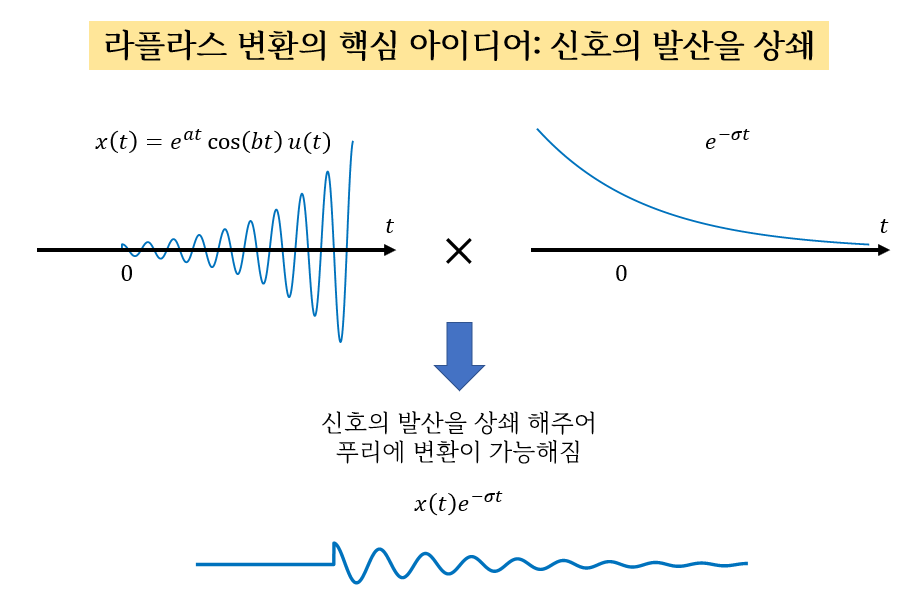
그림 2. 라플라스 변환의 핵심: 발산하는 신호에 감쇄하는 신호를 곱해줘 발산을 방지하여 푸리에 변환할 수 있도록 만듦

가령 $x(t) = e^{2t}\cos(3t)u(t)$와 같았다고 생각해보자. 이 신호는 여전히 시간이 지남에 따라 발산하는 신호이지만 여기에 $e^{-2t}$를 곱해버린다면 $x(t)e^{-2t}=\cos(3t)u(t)$는 푸리에 변환이 존재한다.

그런데, 우리가 임의의 신호 $x(t)$를 받았을 때, 적절한 $\sigma$를 잘 아는 것은 사실상 불가능하다. 따라서 라플라스 변환에서는 가능한 모든 $\sigma\in\mathbb{R}$에 대해 감쇄신호 $\exp(-\sigma t)$를 곱하고 푸리에 변환을 취하게 된다. 그래서 아래 그림과 같이 모든 $\sigma$에 대해 푸리에 변환을 취한 것을 한 평면 상에 모아줄 수 있다.

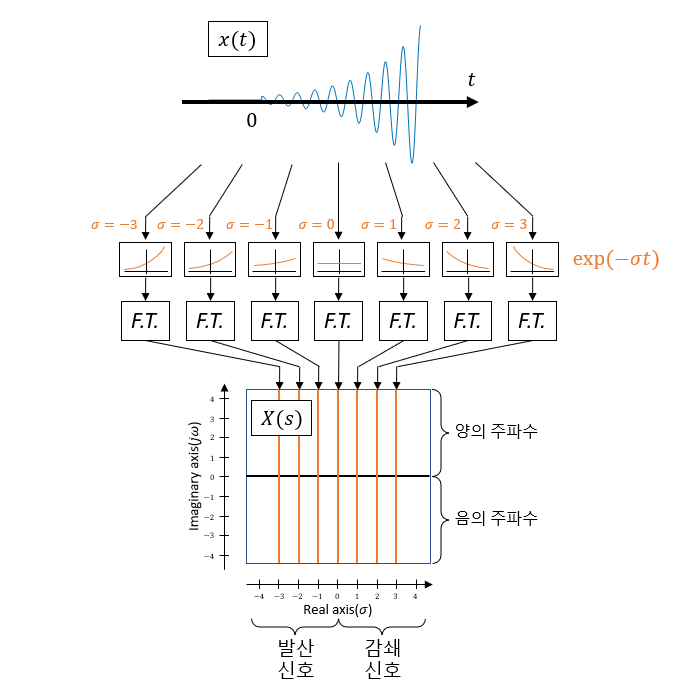
그림 3. 라플라스 변환은 입력 신호에 발산/감쇄하는 지수함수를 곱한 뒤 푸리에 변환을 수행한 것들을 모아둔 결과물이다.

그러므로 라플라스 변환은 푸리에 변환을 살짝 수정하여 다음과 같이 쓸 수 있는 것이다.

원래의 푸리에 변환은 아래와 같다고 하자.

\[X(\omega) = \int_{-\infty}^{\infty}x(t)\exp(-j\omega t)dt\]

여기서 $x(t)$ 대신에 $x(t)\exp(-\sigma t)$를 푸리에 변환 해주게 되면,

\[X(\sigma, \omega)=\int_{-\infty}^{\infty}x(t)\exp(-\sigma t)\exp(-j\omega t)dt\] \[= \int_{-\infty}^{\infty}x(t)\exp(-(\sigma+j\omega)t)dt\]

여기서 $\sigma+j\omega$를 새로운 변수 $s=\sigma+j\omega$라고 하자.

\[\Rightarrow X(s) = \int_{-\infty}^{\infty}x(t)\exp(-st)dt\]

위의 $X(s)$를 $x(t)$에 대한 라플라스 변환이라고 한다.

종종 위와 같은 정의 대신에 적분 구간을 $0$ 부터 $\infty$까지로 써주는 정의를 사용하기도 한다. 이런 라플라스 변환은 unilateral 라플라스 변환이라고 부르고, 시스템 혹은 미분방정식을 분석할 때 주로 사용된다.

\[X(s)=\int_{0^-}^{\infty}x(t)\exp(-st)dt\]

여기서 $0^-$은 $0$에 대한 좌극한이다.

추가로 라플라스 역변환도 존재하는데, 역변환은 복소 선적분이다. 역변환은 식이 복잡하다보니 잘 사용하지 않고 라플라스 변환쌍을 이용해 원래의 신호 $x(t)$를 추정한다.

Region of Convergence(ROC)

라플라스 변환을 공부할 때 중요한 개념 중 하나가 ROC(Region of Convergence)이다. 한국말로 하면 수렴 구간 정도 될 것 같다. 이것의 개념은 위의 그림 3에서 다시 출발할 수 있다. 아주 간단하게 그림 3의 $x(t)$가 다음과 같다고 상정해보자.

\[x(t) = \exp(2t)\cos(3t)u(t)\]

그러면 $\sigma$가 2보다 크다면 푸리에 변환을 취해주기 전에 곱해주는 함수는 아래와 같은 것들일 것이다.

\[\exp(-2t), \exp(-3t), \cdots\]

이러한 함수를 원래의 $x(t)$에 곱하면 이 신호들은 발산하지 않기 때문에 $s-domain$의 $\sigma > 2$인 영역에서는 수렴하는 신호들을 푸리에 변환해주는 것과 같다. 반면에 $\sigma$가 2보다 작은 경우에는 어떨까?

\[\exp(-t), \exp(0), \exp(t), \cdots\]

아마 위와 같은 신호들을 곱해주게 되면 원래의 $x(t)$에 신호를 곱해준다고 하더라도 여전히 발산하고 푸리에 변환은 존재하지 않을 것이다.

그러므로 $x(t) = \exp(2t)\cos(3t)$ 인 경우에는 ROC가 $\sigma>2$라고 할 수 있다.

ROC를 볼 때 가장 기초적이고도 중요한 내용으로써는 ROC가 허수 축을 포함하고 있느냐의 여부인데, 만약 ROC에 허수 축이 포함되는 경우는 $\exp(-\sigma t)$를 곱하지 않더라도 푸리에 변환이 존재한다는 의미이다. 그래서 입력 신호가 impulse response라면 이 시스템은 안정 시스템(Bounded Input Bounded Output, BIBO)이라는 것을 알 수 있다.

라플라스 변환 수행 예시

앞서 예시로 들었던 신호인 $x(t)=e^{2t}\cos(3t)u(t)$에 대해 그림 3의 방식으로 라플라스 변환을 구해보자.

결과는 아래와 같다. 다만, 실제로 라플라스 변환을 수행할 때는 식 (4) 혹은 식 (5)와 같이 계산하며, 아래와 같이 슬라이스 별로 푸리에 변환을 수행하지 않으니 아래는 개념적으로만 이해하는데 도움을 받고 넘어가도록 하자.

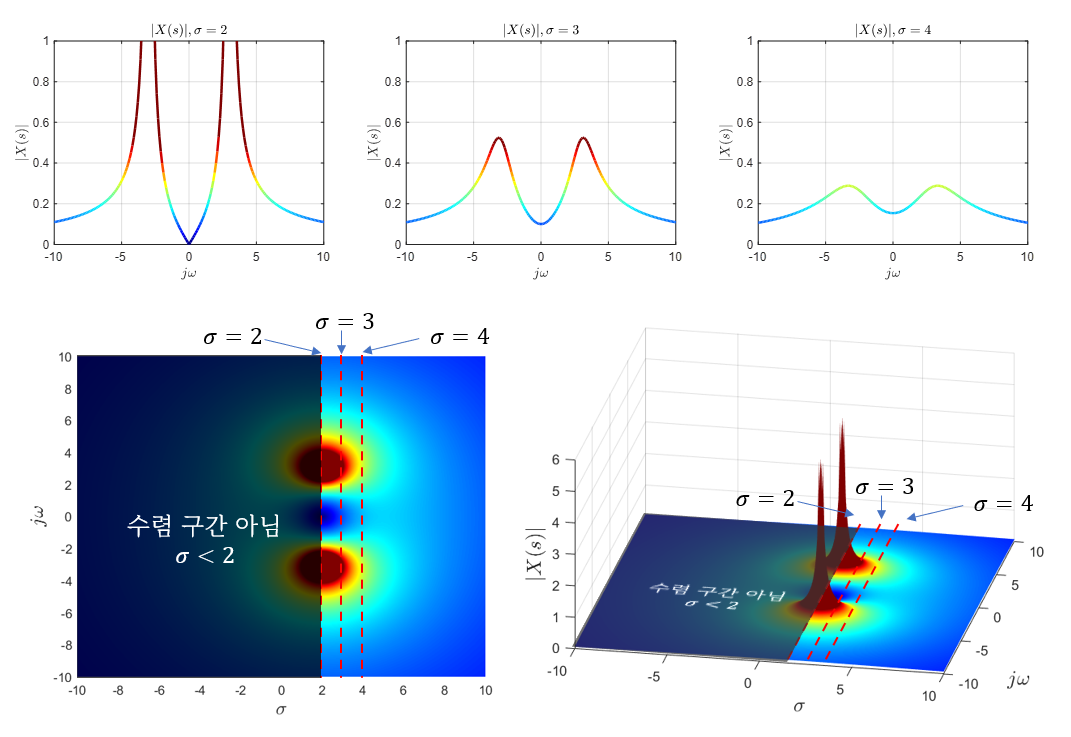
그림 4. $x(t)=e^{2t}\cos(3t) u(t)$에 대한 라플라스 변환을 $\sigma$ 값 별로 슬라이스 하여 확인한 결과

주목해서 봐야하는 점은 라플라스 변환의 결과는 2차원 복소평면 위에 세워진 3차원 그래프라는 점이다. 사실 라플라스 변환의 결과는 복소수로 나오기 때문에 함수의 높이(magnitude) 외에도 위상(phase)에 대한 정보도 함께 담고 있는데, 그림 4에서는 함수의 높이에 관한 부분만 표시했다.

(magnitude와 phase의 정보를 한꺼번에 표현하는 방법에 관한 더 자세한 내용은 허근의 위치 포스팅을 참고해보자.)

눈여겨 볼만한 점들을 몇가지 생각해보자면 다음과 같을 것이다.

우선, $\sigma=2$인 경우 $j\omega=\pm j3$인 경우에 무한대 값을 갖는다는 점이다. 이 결과는 $\sigma=2$일 때 푸리에변환되는 함수는 $x(t)\exp(-2t)=\cos(3t)u(t)$이기 때문이며 $\cos(3t)$의 푸리에 변환은

\[\mathcal{F}\lbrace\cos(3t)\rbrace(\omega)=\pi(\delta(\omega-3)+\delta(\omega+3))\]

과 같기 때문에 $\omega=\pm 3$에서 무한대 값을 갖는 것과 같은 이치라고 볼 수 있다.

두 번째로, $\sigma$ 값이 2보다 커질 수록 결괏값의 magnitude는 감소하게 된다는 것이다. 이것은 매우 자연스러운 결과라고 할 수 있는데 감쇄시키는 신호의 감쇄 정도가 늘어나기 때문에 신호 자체의 크기도 감소하기 때문이다.

마지막으로 $\sigma \lt 2$ 인 구간에서는 3차원 그래프가 그려져 있긴 하지만 실제로는 계산할 수 없는 부분이라는 점을 생각해보아야 한다. 그림 4에서 그려져있는 3차원 그래프는 수렴 구간에서 계산할 수 있는 라플라스 변환의 결과물이다. 실제로 $\sigma \lt 2$인 구간에서는 신호가 발산하기 때문에 푸리에 변환을 구할 수가 없으며 실제로는 결괏값이 존재하지 않는 영역인 것이다.

라플라스 변환의 적용 예시

이제부터는 라플라스 변환을 이용해 문제를 풀어보자.

예시 1

아주 간단한 신호부터 라플라스 변환을 수행해보자. 다음과 같은 unit impulse 함수에 라플라스 변환을 수행해보자.

\[x(t) = \delta(t)\]

위 신호에 대해 라플라스 변환을 계산하면 아래와 같다.

\[X(s) = \int_{-\infty}^{\infty}\delta(t)\exp(-st)dt = \exp(-s(0))=1\]

예시 2

아래의 신호에 대해 라플라스 변환을 계산하시오.

\[x(t)=\exp(at)u(t)\]

여기서 $u(t)$는 unit step function으로 아래와 같은 함수이다.

\[u(t)=\begin{cases} 1 && t \geq 0 \\ 0 && \text{otherwise} \end{cases}\]

또, $a$는 임의의 실수이다.

라플라스 변환은 다음과 같이 계산된다.

\[X(s) = \int_{-\infty}^{\infty}\exp(at)u(t)\exp(-st)dt\] \[=\int_{0}^{\infty}\exp(at)\exp(-st)dt=\int_{0}^{\infty}\exp((a-s)t) dt=\frac{1}{a-s}\exp((a-s)t)\big|_{0}^{\infty}\]

여기서 $s=\sigma+j\omega$로 치환하여 써보면 다음과 같다.

\[\Rightarrow X(s) = \frac{1}{a-\sigma-j\omega}\exp(a-\sigma -j\omega)t\big|_{0}^{\infty}\] \[=\frac{1}{a-\sigma-j\omega}\exp((a-\sigma)t)\exp(j(a_i-\omega)t)\big|_{0}^{\infty}\]

여기서 $\exp((a-\sigma)t)$에 $t=\infty$를 넣는다고 하면 이 함수가 발산하지 않기 위해선 아래의 조건이 만족되어야 한다.

\[a-\sigma \lt 0 \Longrightarrow \sigma \gt a\]

즉,

\[\text{Re}\lbrace s \rbrace \gt a\]

인 조건을 만족해야 한다는 의미이다.

결론적으로 라플라스 변환 $X(s)$는 다음과 같다.

\[X(s) = \frac{1}{a-s}[0-1]=\frac{1}{s-a},\space \text{Re}\lbrace s\rbrace \gt a\]

예시 3

다음과 같은 사각펄스에 대해 라플라스 변환을 구해보자.

\[x(t) = \begin{cases} 1 && 0\lt t \lt \tau \\ 0 && \text{else}\end{cases}\]

위 신호에 대해 라플라스 변환을 계산하면 다음과 같다.

\[X(s) = \int_{0}^{\tau}(1)\exp(-st)dt=\frac{\exp(-st)}{-s}\big|_{0}^{\tau}=\frac{1-\exp(-s\tau)}{s}\]

잘 생각해보면 $s=\sigma+j\omega$이기 때문에 $X(s)$는 $X(\sigma, \omega)$라고 쓸 수도 있다. 다시 말해 입력 변수를 두 개 받는 함수라는 뜻이며 그 출력값이 복소수인 함수이다.

이 함수를 그리기 위해서는 $x, y$ 평면에 $\sigma$, $j\omega$가 오고 $z$축에 $|X(\sigma,\omega)|$와 같이 $X(s)$의 크기가 오는 방법으로 그리는 것이 좋다. (크기 외에도 위상 $\angle X(s)$도 고려할 수 있지만 여기서는 생략하자.)

이것을 그리면 다음과 같은 결과를 얻게 된다.

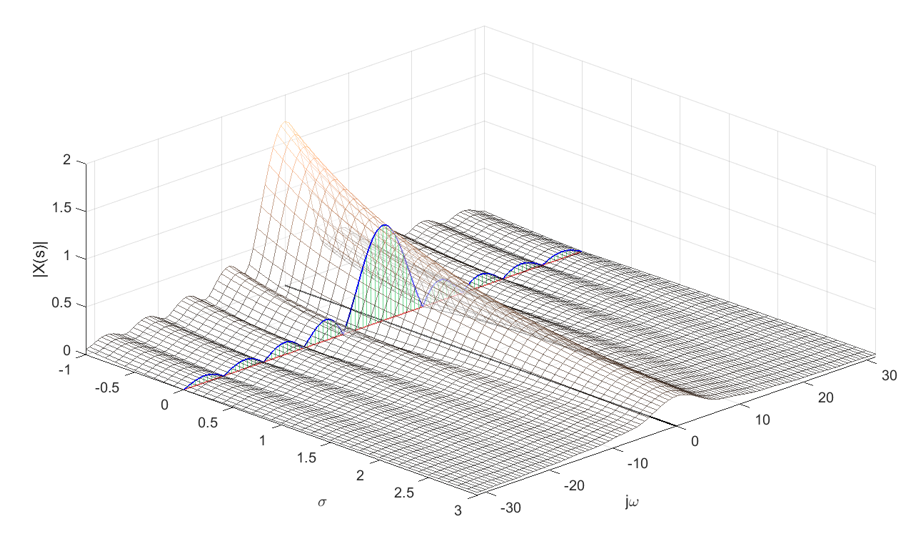
그림 5. 예시 문제에서 $X(s)$의 시각화. 이와 함께 $s=j\omega$인 경우에 해당하는 magnitude plot도 함께 확인할 수 있으며 이는 푸리에 변환의 주파수 응답이다.
코드 소스: Ex 7.7, Ch 7. Laplace Transform, Signals and Systems, Oktay Alkin

이 때, $s=j\omega$ 부분만 따로 떼서 그리면 아래 그림과 같으며, 이것은 사각펄스 $x(t)$의 푸리에 변환 결과에 대해 magnitude만 확인한 것과 같은 것이다.

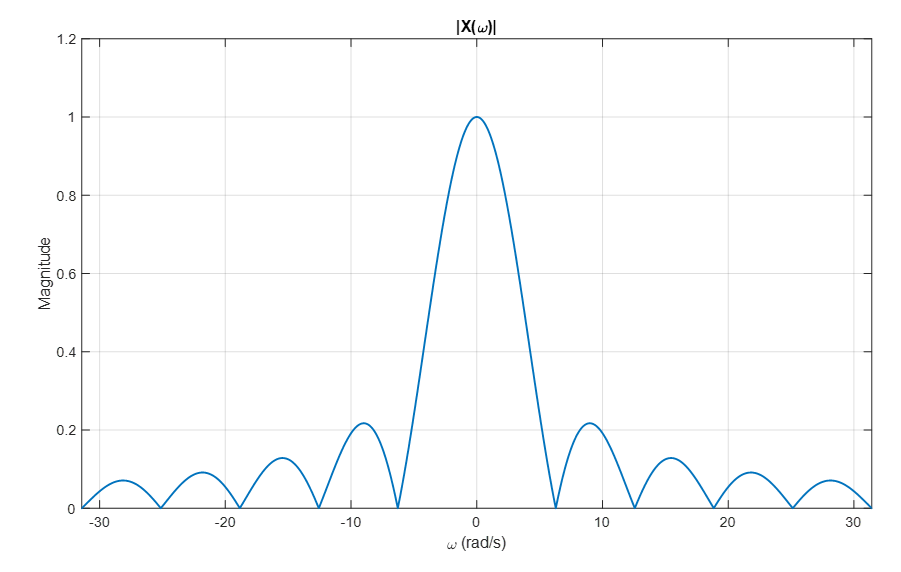
그림 6. 푸리에 변환의 주파수 응답 부분만 따로 떼서 시각화 한 것
코드 소스: Ex 7.7, Ch 7. Laplace Transform, Signals and Systems, Oktay Alkin

pole-zero plot

라플라스 변환 결과는 그림 4 혹은 그림 5에서 처럼 3차원 함수로 표현할 수 있다. 그러나, 그림 4 혹은 그림 5처럼 항상 3차원 그래프로 나타내기에는 사람의 손으로 그리는 것이 거의 불가능하다보니 pole-zero plot이라는 것을 이용해 정보를 나타낸다.

라플라스 변환을 수행한 결과를 보면 그림 4 혹은 그림 7에서 처럼 어떤 $s$ 점에서는 $X(s)$의 크기가 발산하거나 크기가 0이 되는 경우들이 많다. 라플라스 변환에서 가장 중요한 것은 전체적인 3차원 그래프의 형태가 아니라 Region of Convergence가 어디에서 정의되며, 어떤 $s$ 값에서 $X(s)$의 크기가 발산하고 어떤 $s$ 값에서 $X(s)$의 크기가 0이 되는지라고 할 수 있다.

따라서, 2차원 복소평면 상에서 발산하는 $s$의 위치에 x를 그리고 0으로 수렴하는 $s$의 위치에 o를 그려서 이를 표현한다. 이 그래프를 pole-zero plot이라고 부른다.

가령 그림 4에서와 같은 형태의 pole-zero plot은 아래와 같다.

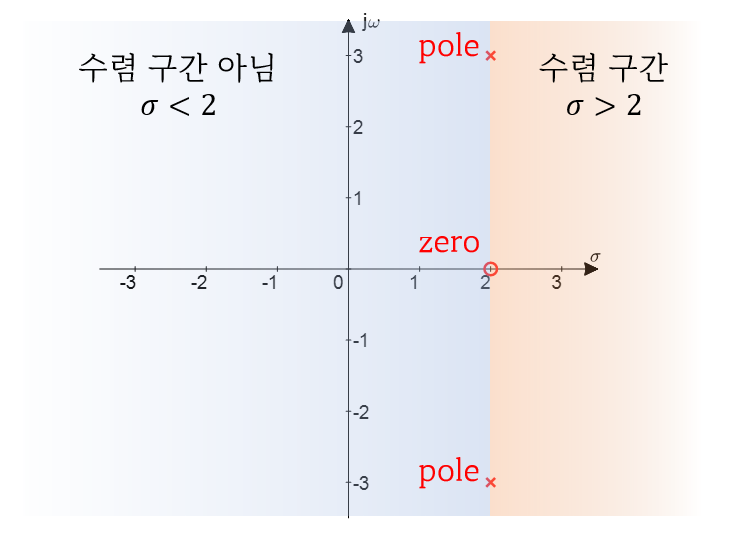
그림 7. 그림 4의 $|X(s)|$를 pole, zero 만으로 표현한 pole-zero plot

일반적으로 라플라스 변환의 결과인 $X(s)$는 아래와 같은 형태를 띈다고 할 수 있다.

\[X(s) = \frac {b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0} {a_ns^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0}\] \[=K\frac {(s-z_1)(s-z_2)\cdots(s-z_{m-1})(s-z_m)} {(s-p_1)(s-p_2)\cdots(s-p_{n-1})(s-p_n)}\]

위 식에서 $z_1, \cdots, z_m$을 zeros라고 하고 $p_1, \cdots, p_n$을 poles라고 한다. 다시 한번 zeros는 $X(s)$가 0이 되도록 만드는 $s$ 값이고 poles는 $X(s)$가 무한대로 발산할 수 있도록 만드는 $s$ 값이다.

라플라스 변환쌍

라플라스 변환을 응용할 때는 위의 예제 1~3에서와 같이 직접 적분을 계산하지 않고, 보통은 잘 알려진 변환쌍을 보고 변환 전/후의 결과물들을 매칭해 사용한다.

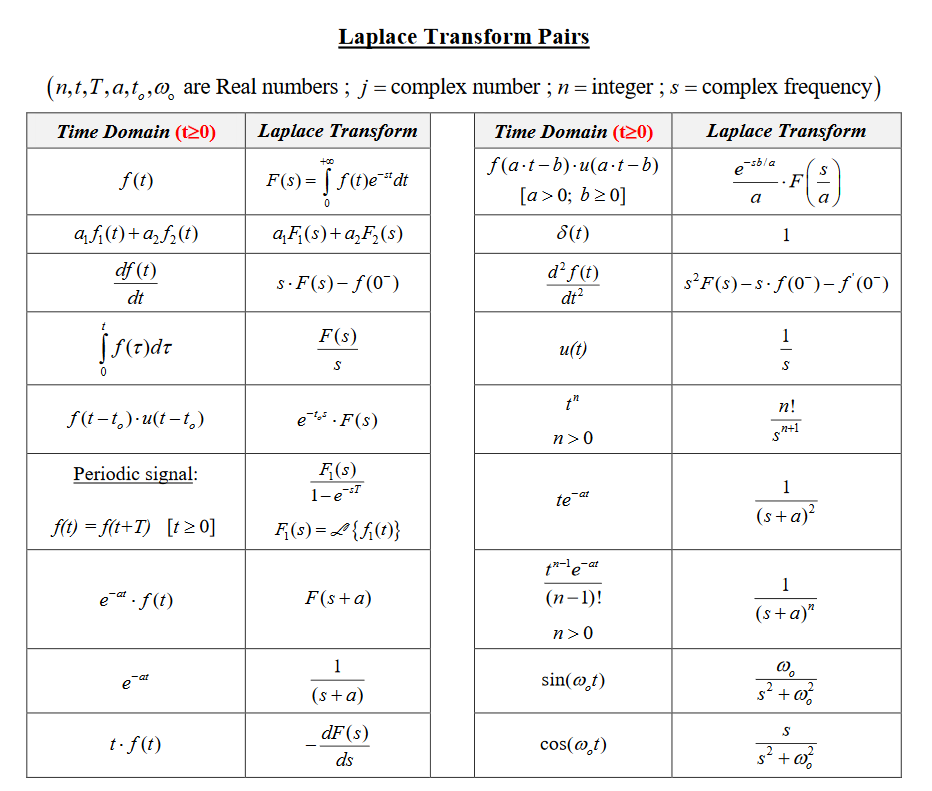
그림 8. 라플라스 변환쌍
출처: Chegg

위 그림에서는 자주 사용되는 라플라스 변환쌍들이 있으니 필요한 것들을 가져다 쓰면 좋을 것 같다.

이 중 우리는 미분계수에 관한 라플라스 변환에 집중해 아래의 내용에서 미분방정식의 풀이를 위한 용법에 대해 좀 더 자세히 생각해보고자 한다.

미분방정식의 풀이를 위한 용법

그림 8의 라플라스 변환쌍 중에는 미분계수에 대한 라플라스 변환 결과가 있다. 수식으로 쓰면 다음과 같다.

\[\frac{d}{dt}f(t) \Longleftrightarrow s\cdot F(s) - f(0^-)\]

여기서 우변의 $f(0^-)$은 신호 $f(t)$의 초기값으로 보통 0으로 놓고 문제를 푸는 경우가 많다. 만약, 특별히 초기값이 지정된다면 초기값은 상수값에 불과하므로 특별히 어렵지 않게 처리할 수 있으니 크게 신경쓰지 않아도 될 문제이다.

또, 2차 미분계수에 관한 라플라스 변환 결과는 다음과 같이 쓰여있는데,

\[\frac{d^2f(t)}{dt^2} \Longleftrightarrow s^2F(s)-s\cdot f(0^-)-f'(0^-)\]

$f(t)$든 $f’(t)$든 모든 $t=0$일 때의 값이 0이라고 가정한다면 미분을 몇번 했던지 관에 관계없이 다음이 성립한다는 것을 알 수 있다.

\[\frac{d^nf(t)}{dt^n} \Longleftrightarrow s^nF(s)\]

즉, 미분 계수 연산자가 단순화되는 것을 알 수 있다.

라플라스 변환을 이용해 미분방정식을 풀면 좋은 점은 크게 두 가지라고 할 수 있다. 첫번째는 어려운 미분방정식의 풀이법이 간단한 대수방정식의 형태로 바뀐다는 점이다. 두번째는 라플라스 변환을 이용하면 비제차미분방정식을 풀 때도 homogeneous solution, particular solution에 대해 따로 고려하지 않고도 한번에 풀어낼 수 있다는 점이다. 비제차 미분방정식에 관해서는 비제차 미분방정식의 의미 편을 참고하도록 하자.

라플라스 변환을 이용한 미분방정식 풀이 예시

예제 1

이 예제는 비제차 미분방정식의 의미 편에 있는 예시와 같은 것이며 초기값 조건을 추가한 것이다.

\[x''-4x'+3x=t; \quad x(0)= 0, x'(0)=0\]

위의 미분방정식에 대해 라플라스 변환을 취해보자.

\[\mathcal{L}\lbrace x''-4x'+3x\rbrace=\mathcal{L}\lbrace t\rbrace\]

라플라스 변환의 선형성에 의해,

\[\Rightarrow \mathcal{L}\lbrace x''\rbrace-4\mathcal{L}\lbrace x'\rbrace+3\mathcal{L}\lbrace x\rbrace=\mathcal{L}\lbrace t\rbrace\]

$x(t)$와 $x’(t)$의 초기값은 모두 0이다. $x(t)$의 라플라스 변환을 $X(s)$라고 하면,

\[\Rightarrow s^2X(s)-4sX(s)+3X(s) = \frac{1}{s^2}\] \[=(s^2-4s+3)X(s)=\frac{1}{s^2}\] \[\Rightarrow X(s) = \frac{1}{s^2(s-1)(s-3)}\]

여기서 부분 분수로 위의 식을 분할해보자.

\[\Rightarrow X(s) = \frac{a}{s}+\frac{b}{s^2}+\frac{c}{s-1}+\frac{d}{s-3}\]

다시 원래의 분수로 합쳐보면,

\[\Rightarrow \frac {as(s^2-4s+3)+b(s^2-4s+3)+cs^2(s-3)+ds^2(s-1)} {s^2(s-1)(s-3)}\] \[=\frac {s^3(a+c+d)+s^2(-4a+b-3c-d)+s(3a-4b)+3b} {s^2(s-1)(s-3)}\]

따라서 위 식의 분자는 1이라는 값을 가져야 한다. 그러므로 우선

\[b=\frac{1}{3}\]

이고, 나머지 세 개의 식을 연립하자.

\[\begin{cases}a+c+d = 0 \\ -4a+1/3-3c-d = 0 \\ 3a-4\cdot(1/3) = 0\end{cases}\]

그러면 결과로써 다음과 같은 결과를 얻는다.

\[a=\frac{4}{9}, b = \frac{1}{3}, c = -\frac{1}{2}, d = \frac{1}{18}\]

그러므로 $X(s)$를 다시 써보면,

\[X(s) = \left(\frac{4}{9}\cdot\frac{1}{s}\right)+\left(\frac{1}{3}\cdot\frac{1}{s^2}\right)+\left(\left(-\frac{1}{2}\right)\cdot\frac{1}{s-1}\right)+\left(\frac{1}{18}\cdot\frac{1}{s-3}\right)\]

이 $X(s)$를 다시 라플라스 역변환하면 다음과 같다.

\[x(t) = \frac{4}{9}+\frac{1}{3}t-\frac{1}{2}e^t+\frac{1}{18}e^{3t}\]

여기서 역변환에 이용한 라플라스 변환쌍은 다음과 같다.

\[\begin{cases}\mathcal{L}\lbrace u(t)\rbrace=1/s \\ \mathcal{L}\lbrace tu(t)\rbrace=1/s^2\\ \mathcal{L}\lbrace e^{at}\rbrace=1/(s-a)\end{cases}\]

참고문헌

• Signals and systems, Oktay Alkin, CRC Press
• 7. Laplace transform, EEE2047S: Signals and Systems I, Fred Nicolls, University of Cape Town