Non-negative Matrix Factorization(NMF)

Prerequisites

이번 포스팅을 이해하기 위해선 아래의 내용에 대해 잘 알고 오시는 것을 추천드립니다.

독립성분분석은 내용이 어려운 편이기 때문에 꼭 다 이해하실 필요는 없습니다만, 주성분분석과 경사하강법은 알고오시는 것을 추천드립니다.

NMF의 정의

음수 미포함 행렬 분해(Non-negative Matrix Factorization, NMF)는 음수를 포함하지 않는 행렬 $X$를 음수를 포함하지 않는 행렬 $W$와 $H$의 곱으로 분해하는 알고리즘이다

수식으로 표현하자면 다음과 같다.

\[X = WH\]

W와 H의 의미

$W$와 $H$의 의미에 대해 이해하기에 앞서 우리가 분해하고자 하는 행렬 $X$가 어떤 것일지 생각해보도록 하자.

행렬 $X$는 데이터셋으로 생각하면 좋을 것 같다. 가령 $X$가 $m\times n$행렬이라고 한다면 여기서 $m$은 데이터 샘플의 갯수(the number of observation), $n$은 각 데이터 샘플 벡터의 차원(the dimension of a data)라고 볼 수 있다.

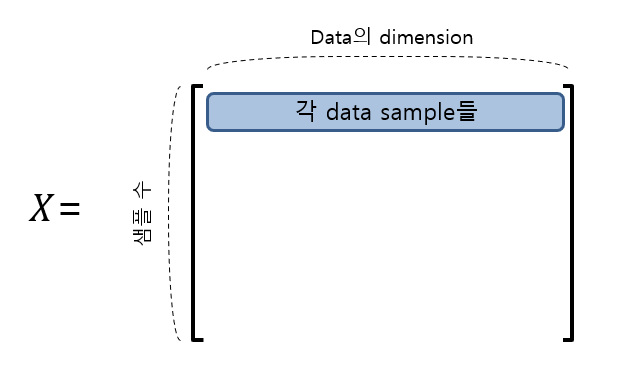
그림 1. 데이터 행렬 $X$의 형태

한편, 행렬 $W$와 $H$의 차원은 사용자의 필요에 맞게 결정해줄 수가 있다. 물론 $W$의 행의 갯수와 $H$의 열의 갯수는 각각 $m$과 $n$이 되어야 한다.

가령, $p$개의 feature를 가지고 원래의 데이터셋 $X$를 분해하고 싶다고 하면, $W$와 $H$의 차원은 다음과 같이 결정될 것이다.

\[W\in \Bbb{R}^{m\times p}\] \[H\in \Bbb{R}^{p\times n}\]

이렇게 분해해주게 되었을 대 우선 $H$부터 생각해보면 $H$의 각 행은 하나의 feature가 되며, $W$의 한 행은 각각의 feature들을 얼마만큼 섞어 쓸 것인지에 관한 weight의 의미를 갖게 된다.

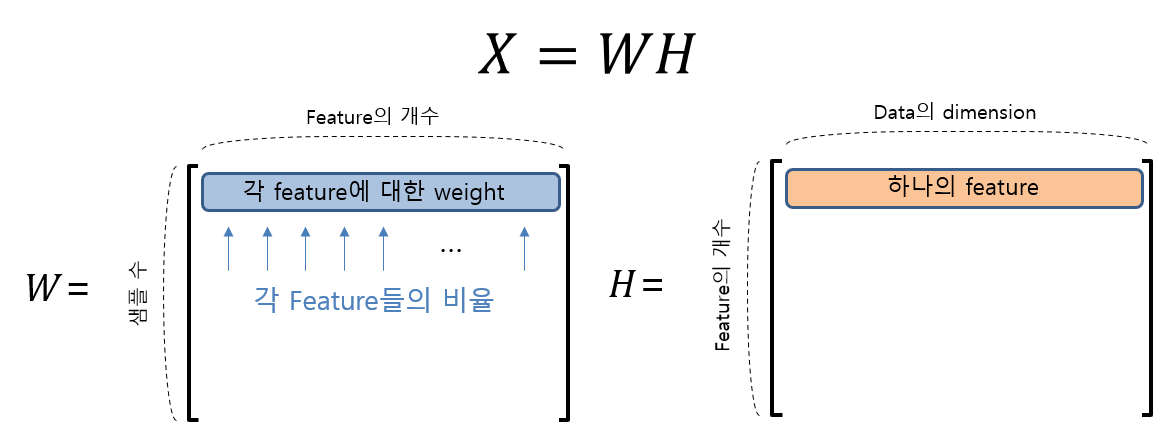
그림 2. NMF를 이용해 분해된 행렬 $W$와 $H$의 형태와 각 행렬의 행의 의미

왜 NMF를 쓰는 것이 유용할 수 있을까?

non-negative 데이터는 non-negative feature로 설명하는 것이 좋다.

NMF가 유용한 이유 중 하나는 추출하게 되는 feature들이 모두 non-negative feature이기 때문이다.

우리가 다루게 되는 데이터들 중 어떤 데이터들은 음수 값이 포함되지 않는 데이터들이 있다.

예를 들어 그림의 경우 모든 데이터들은 pixel의 세기로 구성되어 있고, 이 값들 중 음수는 없을 것이다.

그렇다면 가령 이 데이터가 어떤 feature들이 적절히 배치된 것이라고 한다면,

가령, 얼굴의 눈, 코, 입, 귀 등의 그림이 적절히 합쳐진 것이라고 하면 이 feature들은 모두 음수가 아닌 값들로 구성되어 있다고 보는 것이 자연스럽다.

그런데, 많은 경우에 사용되는 matrix factorization 방법들(가령, SVD)이나 차원 감소 방법(요인 분석, 주성분 분석, cluster 분석 등)에서는 획득할 수 있는 feature들이 음수이면 안된다던지 하는 제한사항같은 것은 없기 때문에 데이터의 특성인 non-negativity를 보존할 수 있다는 보장을 받을 수 없다는 한계점이 있다.

feature들의 독립성을 잘 catch 할 수 있다.

또, NMF를 사용하면 좋은 이유 중 하나는 NMF는 PCA나 SVD와 같은 factorization 방법에 비해서 데이터 구조를 조금 더 잘 반영할 수 있기 때문이다.

PCA나 SVD는 feature들 간의 직교성이 보장된다. 알고리즘 자체가 그렇게 설계된 것이기 때문이다.

PCA만 가지고 설명하면 PCA는 covariance matrix의 eigenvector를 이용한 분해인데, covariance matrix는 symmetric matrix이므로 eigenvector들은 항상 직교한다는 것을 수학적으로 증명할 수 있다.

(좀 더 자세한 설명에 대해선 PCA와 SVD 편을 참고해서 확인하길 바란다.)

하지만 feature 벡터들이 서로 직교하게 되면 데이터셋의 실제 데이터 구조를 잘 반영하지 못하게 될 수도 있다. 아래의 그림을 통해 PCA와 NMF의 차이를 확인해보도록 하자.

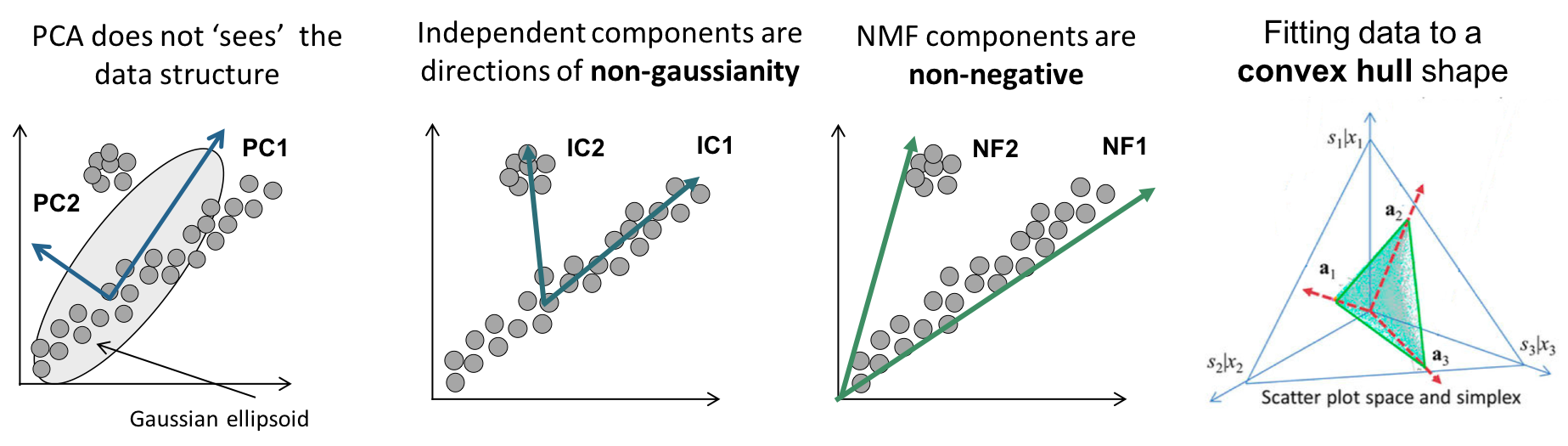
그림 3. PCA와 NMF의 기하학적인 해석
그림 출처

필요한 선행 테크닉

그렇다면, 본격적으로 NMF의 결과물인 $W$, $H$를 구하는 방법을 이해하기에 앞서 우리가 필요한 선행지식을 몇 가지 알고 가보도록 하자.

대각합 연산자(trace)

간간히, 행렬의 원소 중 대각 성분만 필요한 경우가 있다. 특히, 대각합 성분만 필요한 경우가 있는데 이 때 사용할 수 있는 연산자가 대각합(trace)연산자이다.

다시 말해 trace 연산자는,

\[tr\left(\begin{bmatrix}a_{11} && a_{12} && a_{13} \\ a_{21} && a_{22} && a_{23}\\a_{31} && a_{32} && a_{33}\end{bmatrix}\right) = a_{11}+a_{22}+a_{33}\]

과 같다.

여기서 trace 연산의 몇 가지 성질을 적어보자면 다음과 같다.

\[tr(A+B) = tr(A) + tr(B)\] \[tr(ABC) = tr(CAB) = tr(BCA)\]

또, trace가 포함된 두 개 이상의 행렬곱에 대해 행렬에 대한 미분(즉, gradient)은 다음과 같다.

이 내용은 아래에서 NMF의 알고리즘을 유도할 때 유용하게 이용될 것이기 때문에 네 개의 식은 눈여겨두고 가도록 하자.

\[\nabla_X tr(AX) = A^T\] \[\nabla_X tr(X^TA) = A\] \[\nabla_X tr(X^TAX) = (A+A^T)X\] \[\nabla_X tr(XAX^T) = X(A^T+A)\]

행렬의 크기를 계산하는 법

일반적으로 벡터의 크기를 노름(norm)이라고 부른다. (영어로 읽는 셈 치고 ‘놈’이라고 읽는 경우도 흔하다.)

행렬 역시도 일반적인 벡터의 성질(스칼라배와 벡터 간의 합)을 만족하기 때문에 일반적인 의미의 벡터로 볼 수 있다.

따라서, 행렬의 크기를 구하는 방법으로 일반적인 벡터의 크기를 구하는 방법인 norm 계산 방법을 차용해 쓰는 것은 문제없는 것이다.

norm의 종류는 어려가지인데, 여기서는 프로베니우스(Frobenius) norm에 대해서만 간단하게 알아보자.

가령, 아래와 같은 행렬 $A$가 있다고 생각해보자.

\[A = \begin{bmatrix}a & b \\ c & d\end{bmatrix}\]

이 행렬의 크기는 다음과 같은 방법으로 생각하면 무리가 없을 것이다.

\[\text{size} = \sqrt{a^2 + b^2 + c^2 + d^2}\]

여기서 이제부터는 size라는 이름 대신에 $||A||_F$ 라고 쓰고 이것을 행렬 A의 Frobenius norm이라고 부르자.

또, 이 norm을 계산하는 방법은 아래와 같이 계산할 수도 있을 것이다.

\[A^TA =\begin{bmatrix}a & c \\ b & d\end{bmatrix}\begin{bmatrix}a & b \\ c & d\end{bmatrix}\] \[=\begin{bmatrix}a^2+c^2 & ab+cd \\ ab+cd & b^2 + d^2 \end{bmatrix}\]

위의 마지막 결과에서 우리가 필요한 것은 대각합만 필요한 것을 알 수 있다.

따라서, 행렬 A의 Frobenius norm은 다음과 같이도 구할 수 있다.

\[\|A\|_F = \sqrt{tr(A^T A)}\]

일반적으로 $m\times n$ 사이즈의 행렬에 대해 Frobenius norm은 다음과 같이 정의할 수 있다.

\[\|A\|_F = \sqrt{\sum_{i=1}^m\sum_{j=1}^n |a_{ij}|^2} = \sqrt{tr(A^TA)}\]

원소별 곱

또, 가끔 행렬을 다루다보면 일반적인 행렬의 곱이 아니라 원소별 곱이 필요한 경우가 있다.

원소별 곱은 element-wise product 혹은 Hadamard product 라고 부른다 (한국어로 읽을 때 정식명칭은 ‘아다마르 곱’이다.).

원소별 곱은 말 그대로 행렬의 각 성분을 곱하는 연산인데, 같은 크기의 행렬에 대해서만 수행할 수 있다는 점은 생각해보면 당연하다.

가령, 아래와 같이 두 행렬을 원소별 곱 처리할 수 있다. 원소별 곱의 기호는 $\circ$이다.

\[A = \begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\] \[B = \begin{bmatrix}a & b \\ c & d\end{bmatrix}\] \[A\circ B = \begin{bmatrix}1a & 2b \\ 3c & 4d\end{bmatrix}\]

NMF의 update 규칙

\[H:= H\circ\frac{W^TX}{W^TWH}\] \[W:= W\circ\frac{XH^T}{WHH^T}\]

여기서 ‘$\circ$’는 원소별 곱(element-wise product)을 표현한 것이다.

또, 나누기 연산도 원소별 나누기 연산을 표현한 것이다.

update 알고리즘의 유도과정

우리는 임의의 행렬 $X$를 분해하여 얻게 된 $W, H$가 최대한 $X$에 가깝기를 바란다.

따라서, 목적함수는 $X$에서 $WH$까지의 Frobenius norm으로 정의하는 것은 무리가 없다.

\[\|X-WH\|^2_F =tr((X-WH)^T(X-WH))\]

NMF는 iterative한 방식으로 분해가 수행된다. 따라서, 업데이트의 방식은 gradient descent를 이용하는 것이 좋은 방법 중 하나이다.

\[H:=H-\eta_H\circ \nabla_H\|X-WH\|_F^2\] \[W:=W-\eta_W\circ \nabla_W\|X-WH\|_F^2\]

식 (22)을 조금 더 전개하면 아래와 같다.

\[\|X-WH\|_F^2 = tr\left((X-WH)^T(X-WH)\right)\] \[=tr\left((X^T - H^TW^T)(X-WH)\right)\] \[=tr\left(X^TX-X^TWH-H^TW^TX + H^TW^TWH\right)\]

이제 위의 trace와 관련된 성질들을 이용하여 $W$와 $H$에 대한 partial derivative를 계산하면 다음과 같이 계산할 수 있다.

\[\nabla_H \|X-WH\|_F^2 = \nabla_H\left\lbrace tr(X^TX)-tr(X^TWH)-tr(H^TW^TX)+tr(H^TW^TWH)\right\rbrace\] \[=0 - (X^TW)^T - W^TX + (W^TW+(W^TW)^T)H\] \[=-2W^TX+2W^TWH\] \[\nabla_W \|X-WH\|_F^2 = \nabla_W\left\lbrace tr(X^TX) - tr(X^TWH) - tr(H^TW^TX) + tr(H^TW^TWH)\right\rbrace\] \[=0-\nabla_W tr(HX^TW) - \nabla_W tr(W^TXH^T) + \nabla_W tr(WHH^TW^T)\] \[=-(HX^T)^T - XH^T + W((HH^T)^T + HH^T)\] \[=-2XH^T + 2WHH^T\]

따라서 식 (30)과 식 (34)의 결과를 식(23), 식(24)에 대입하면,

\[식 (23) \Rightarrow H:= H+\eta_H\circ(W^TX-W^TWH)\] \[식 (24) \Rightarrow W:= W+\eta_W\circ(XH^T-WHH^T)\]

여기서 원래 식(30)과 (34) 있던 숫자 2는 무시되었다.

그런데 식 (35)와 식 (36)를 보면 음수 term이 포함되어 있는 것을 알 수 있다.

즉, 이 과정에서 $H$와 $W$가 음수가 포함될 수 있게 된다. NMF의 가장 중요한 제약사항은 $H$와 $W$가 모두 음수를 포함하지 않아야 하므로 NMF에서는 특별한 방식으로 Gradient Descent를 수행하게 된다.

그 방법은 바로 learning rate $\eta$를 data-driven 방법으로 특별하게 정의하는 것이다. Lee and Seung(2001)에서는 learning rate을 다음과 같이 정의하는 것을 제안하고 있다.

\[\eta_H = \frac{H}{W^TWH}\] \[\eta_W = \frac{W}{WHH^T}\]

여기서 분수꼴의 표시는 element-wise division을 의미한다.

이렇게 learning rate을 이용하게 되면 식(35)과 식(36)은 다음과 같이 변형되게 된다.

\[식(35) \Rightarrow H:=H+\frac{H}{W^TWH}\circ (W^TX-W^TWH)\] \[=H+H\circ\frac{W^TX}{W^TWH}-H\circ\frac{W^TWH}{W^TWH}\]

여기서

\[\frac{W^TWH}{W^TWH}= I\]

이므로, (분수 표시는 elementwise-division임을 다시 한번 생각하도록 하자!)

\[H\circ\frac{W^TWH}{W^TWH} = H\]

이다.

따라서,

\[\Rightarrow H + H\circ\frac{W^TX}{W^TWH}-H=H\circ\frac{W^TX}{W^TWH}\]

이므로, update rule은

\[\therefore H:=H\circ\frac{W^TX}{W^TWH}\]

가 된다.

이렇게 해주게 되면 $H$는 음의 값을 가질 수 없게 update 될 수 있다.

마찬가지 방법으로 $W$에 대한 update rule을 계산하면,

\[식(36)\Rightarrow W:=W+\frac{W}{WHH^T}\circ(XH^T-WHH^T)\] \[=W+W\circ\frac{XH^T}{WHH^T}-W\circ\frac{WHH^T}{WHH^T}=W\circ\frac{XH^T}{WHH^T}\]

가 된다.

Lee and Seung(2001)에서는 이런 방식으로 learning rate을 선택하더라도 여전히 수렴성이 보장된다는 것을 증명하였다.

NMF 적용 결과

아래의 내용은 Yale Extended Face Data 를 이용해 NMF와 PCA로 feature 추출을 시도한 결과이다.

Yale Extended Face Data는 38명의 사람으로부터 얻은 32x32 사이즈의 얼굴 사진이 데이터로 포함되어 있다.

아래는 데이터셋의 일부이다.

그림 4. Yale Extended Face DAta 데이터 셋의 일부 그림

해당 데이터에 NMF와 PCA를 적용시켰을 때의 결과는 아래의 그림 5, 그림 6과 같다.

그림 5. NMF 적용을 통해 얻은 25개의 feature set

그림 6. PCA 적용을 통해 얻은 25개 feature set

데이터셋이 가지고 있는 빛의 방향이나 형태적인 요소들을 NMF를 이용해 얻은 feature들이 잘 반영하고 있는 것을 알 수 있다.

또한, NMF의 feature들은 많은 값들이 0으로 채워져 있으며, 이것을 생각하면 feature를 저장하는데 용량이 다소 적게들 수 있음을 알 수 있다.

또, PCA를 통해 얻은 feature들에 비해서 NMF로 얻은 feature들은 feature의 의미가 상대적으로 뚜렷해보인다.

NMF 적용 결과 epoch 별 feature 정리

MATLAB 코드

아래는 NMF와 PCA를 적용한 MATLAB 소스코드이다.

clear; close all; clc;

load('YaleB_32x32.mat'); % gnd는 사람 번호인듯.
% 출처: http://www.cad.zju.edu.cn/home/dengcai/Data/FaceData.html
% 사용한 데이터셋의 이름은 Extended Yale Face Database B임.

figure('position',[556, 237, 947, 699]);
for i= 1:25
    subplot(5,5,i)
    imagesc(reshape(fea(i,:), 32, 32)); colormap('gray')
end

%% NMF 수행하기
% n_features = 25;
% [W, H] = nnmf(fea, n_features); %MATLAB 함수 이용 시

% 직접 코딩해보기
m = size(fea,1);
n = size(fea,2);
p = 25; % the number of features
rng(1)
W = rand(m, p)*255;
H = rand(p, n)*255;
n_epoch = 200;
X = fea;
for i_epoch = 1:n_epoch
    H = H.*((W'*X)./(W'*W*H));
    W = W.*((X*H')./(W*(H*H')));
end

n_features = p;

figure('position',[556, 237, 947, 699]);
for i_features = 1:n_features
    subplot(5,5,i_features)
    imagesc(reshape(H(i_features,:), 32, 32)); colormap('gray');
end

% figure; imagesc(reshape(randn(1, 25) * H, 32, 32)); colormap('gray')

%% PCA 수행하기

[coeff, score, latent] = pca(fea);

figure('position',[556, 237, 947, 699]);
for i_features = 1:n_features
    subplot(5,5,i_features)
    imagesc(reshape(coeff(:, i_features), 32, 32)); colormap('gray');
end

참고자료

이전특이값 분해(SVD)

다음자코비안 행렬의 기하학적 의미