오일러 방법을 통한 dy/dx = x의 솔루션으로의 근사치 플롯

Prerequisites

이 내용을 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 미분방정식을 이용한 현상 모델링

미분 방정식을 보는 또 다른 관점

미분 방정식을 이용한 현상 모델링편에서는 어떻게 미분방정식을 이용해 현상을 모델링 할 수 있는지 알아보았다.

이 때 이용되었던 미분방정식은 대부분 단순한 1계 미분방정식의 꼴을 갖고 있었는데, 아래와 같은 형태였다.

\[\frac{dy}{dx}=f(x,y) % 식 (1)\]

위 식은 좌변에는 미분 계수, 우변에는 다항식이 들어있다라고 볼 수도 있지만, 다른 방식으로 생각해보면 $x, y$ 좌표계 상에 있는 $f(x,y)$라는 함수값이 미분 계수로 정의되어 있는 식이라고도 볼 수 있다.

다시 말해, 모든 $(x, y)$의 좌표에 대해 기울기가 정의되어 있는 형태라고도 볼 수 있는 것이다.

그러면 다음과 같이 미분계수를 모든 좌표에 적용한 형태의 결과값을 얻을 수 있게 되고 이러한 그림을 방향장(direction field) 혹은 기울기장(slope field)라고 부른다.

아래 그림의 예시에서는 다음과 같은 미분방정식에 대한 방향장을 도시하였다.

\[\frac{dy}{dx}=x % 식 (2)\]

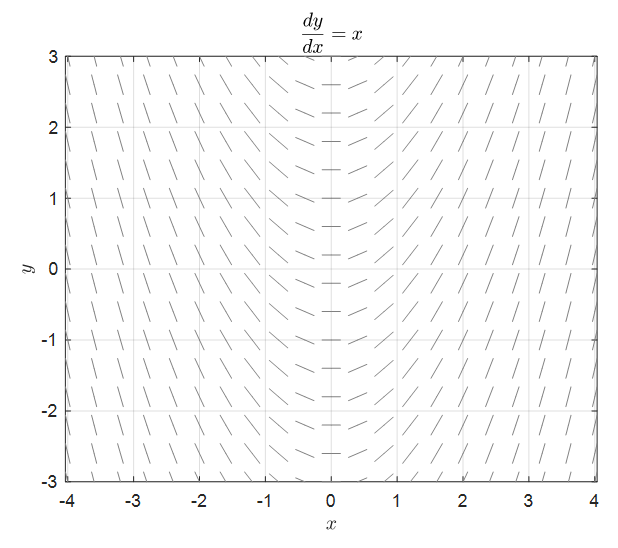
그림 1. dy/dx = x 의 방향장

그림 1에서 볼 수 있는 것은 dy/dx라는 미분계수 혹은 기울기는 x의 좌표값에 따라 바뀌게 된다는 점이다.

아주 간단한 미분방정식으로부터 얻는 식이지만, 방향장을 공부하기에는 아주 좋은 예시라고 할 수 있을 것 같아 가져왔다.

그럼 우리가 이런 방향장을 얻게됨으로써 미분방정식을 풀이하는데 어떤 이점이 있을까?

결국 미분방정식을 연구함으로써 얻을 수 있는 최후의 결과물은 이 방정식의 해(solution)와 관련된 것이니, 분명 해를 구하는 것과 관련이 있는 개념이어야 할 것이다.

오일러 방법을 이용한 solution 구하기

그림 1에서 이용한 미분방정식 식 (2)를 다시 확인해보자.

\[\frac{dy}{dx} = x \notag\]

식 (2)에 있는 좌변은 변화율이다. 다시 말해, 식 (2)의 미분 방정식은 함수 위의 순간 순간의 변화가 입력해준 $x$ 값에 따라 어떻게 다른지를 말해주고 있는 것이라고 할 수 있다.

과연 미분 방정식에서 말하는 ‘변화’란 무엇일까?

변화: 다음 포인트 함수값과의 차이

식 (2)에는 미분 계수 $dy/dx$가 들어있다보니 식이 어려워 보일 수 있다. 미분 계수를 원래의 정의대로 돌려놓고 생각해보자.

다시 말해, $y=f(x)$라고 했을 때,

\[식(2) \Rightarrow \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}=x % 식 (3)\]

와 같이 풀어 쓸 수 있다.

이 식에 대해 기하학적으로 생각해보면 다음의 그림 2와 같이 생각할 수 있다.

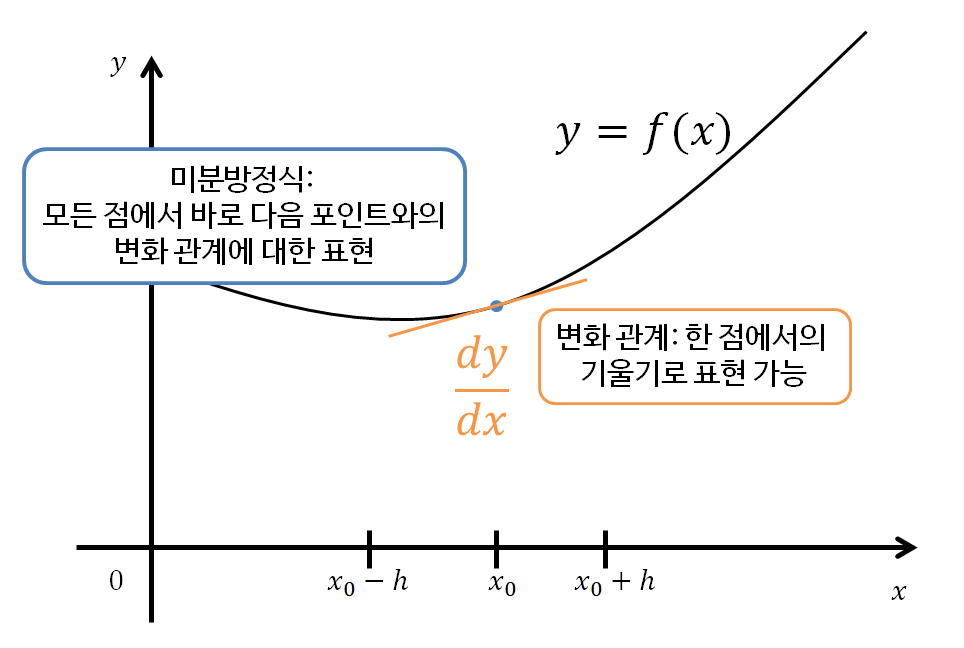
그림 2. 미분 방정식의 기하학적 의미

다시 말해, 미분 방정식에서의 미분 계수를 통해 바로 옆 정의역의 값에 대한 함수를 예측할 수 있게 된다.

이것에 대한 의미를 조금 더 생각해보기 위해 $h$가 1인 경우부터 조금씩 값을 줄여나가보자.

$h=1$인 경우

\[식(3)\Rightarrow f(x+1)-f(x) = x % 식 (4)\] \[\Rightarrow f(x+1) = x + f(x) % 식 (5)\]

즉, 식 (5)가 말하는 것은 일종의 점화식이다. 만약, $f(0)=0$이라는 초기값을 설정해보면 다음과 같이 $f(1), f(2), \cdots$을 구할 수 있다.

\[f(1) = 0 + f(0) = 0 + 0 = 0 % 식 (6)\] \[f(2) = 1 + f(1) = 1+ 0 = 1 % 식 (7)\] \[f(3) = 2 + f(2) = 2 + 1 = 3 % 식 (8)\] \[f(4) = 3 + f(3) = 3 + 3 = 6 % 식 (9)\] \[\vdots\notag\]

반대로 f(-1)과 같은 값들도 구할 수 있다. 식 (5)를 $x$를 좌변으로 옮겨 다시 써주면,

\[f(x) = f(x+1) - x % 식 (10)\]

이므로,

\[\Rightarrow f(x-1) = f(x) - (x-1) % 식 (11)\]

이다. 따라서,

\[f(-1) = f(0) - (-1) = 0 + 1 = 1 % 식 (12)\] \[f(-2) = f(-1) - (-2) = 1 + 2 = 3 % 식 (13)\] \[f(-3) = f(-2) - (-3) = 3 + 3 = 6 % 식 (14)\]

일부 값을 표로 정리하면 다음과 같다.

그리고 이것을 그래프로 그리면 다음과 같다.

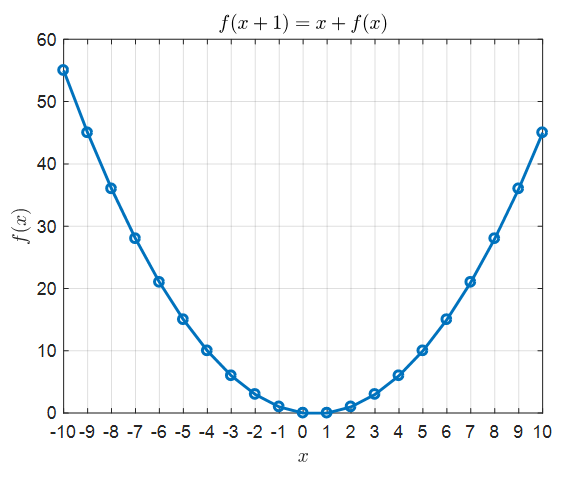
그림 3. 식 (5) 점화식의 solution을 그래프에 옮긴 것

$h = 0.5$인 경우

$h=0.5$라면 식 (3)은 다음과 같이 변하게 될 것이다.

\[식(3)\Rightarrow \frac{f(x+0.5)-f(x)}{0.5} = x % 식 (15)\] \[\Rightarrow f(x+0.5) = 0.5x + f(x) % 식 (16)\]

식 (5)와 마찬가지로 식 (16) 역시도 점화식의 개념으로 생각해볼 수 있으며 $f(0)=0$이라는 초기 조건을 이용하면 $f(0.5), f(1), f(1.5)$ 등의 값을 얻을 수 있다.

마찬가지로 아래와 같이 식 (16)을 조금 조정하면 $f(-0.5), f(-1)$ 등의 값 또한 얻을 수 있다.

\[\Rightarrow f(x-0.5)= f(x) - 0.5 (x-0.5) % 식 (17)\]

일부 값을 표로 정리하면 아래와 같다.

그리고 이것을 그래프로 그리면 다음과 같다.

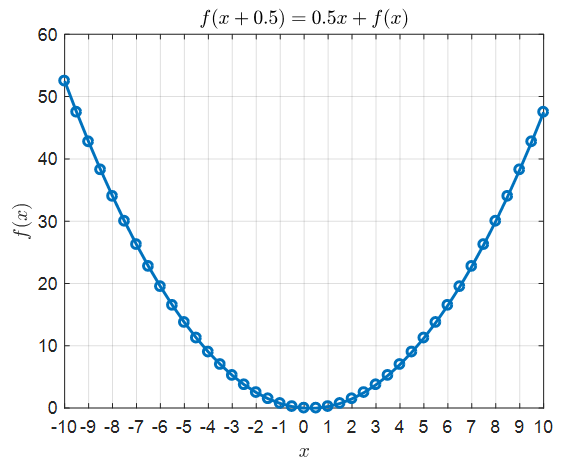
그림 4. 식 (16) 점화식의 solution을 그래프에 옮긴 것

$h=0.1$인 경우

$h=0.1$인 경우에도 위의 방법을 그대로 따라가서 점화식을 만들면 아래와 같으며,

\[식(3)\Rightarrow \frac{f(x+0.1)-f(x)}{0.1} = x % 식 (18)\]

같은 방법을 통해 그래프로 점화식의 solution을 그리면 다음과 같다.

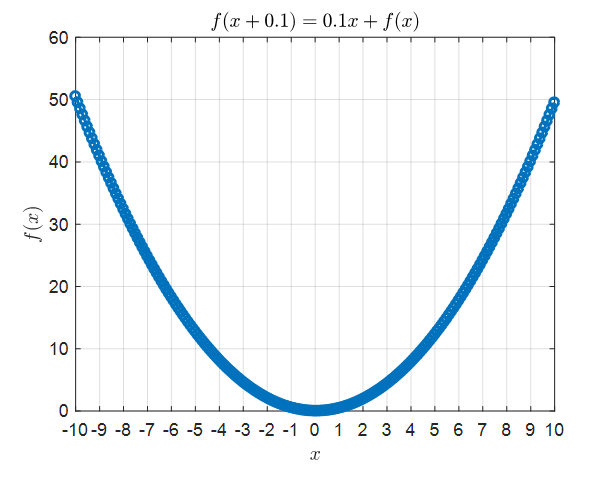
그림 5. 식 (18) 점화식의 solution을 그래프에 옮긴 것

식 (2)의 진짜 solution과 그림 2-4의 비교

그런데, 식 (2)는 다시 이렇게도 쓸 수 있는 것이다.

\[식(2) \Rightarrow f'(x)= x % 식 (19)\]

식 (19)는 양변을 적분하고 $f(0)=0$이라는 초기값을 넣어주면 다음과 같은 결과를 얻을 수 있다.

\[f(x) = \frac{1}{2}x^2\]

즉, $f(x)=\frac{1}{2}x^2$가 식 (2)를 만족시키는 해라고 할 수 있는데, 이 값을 그림 2~4에서 그린 값과 비교해보자.

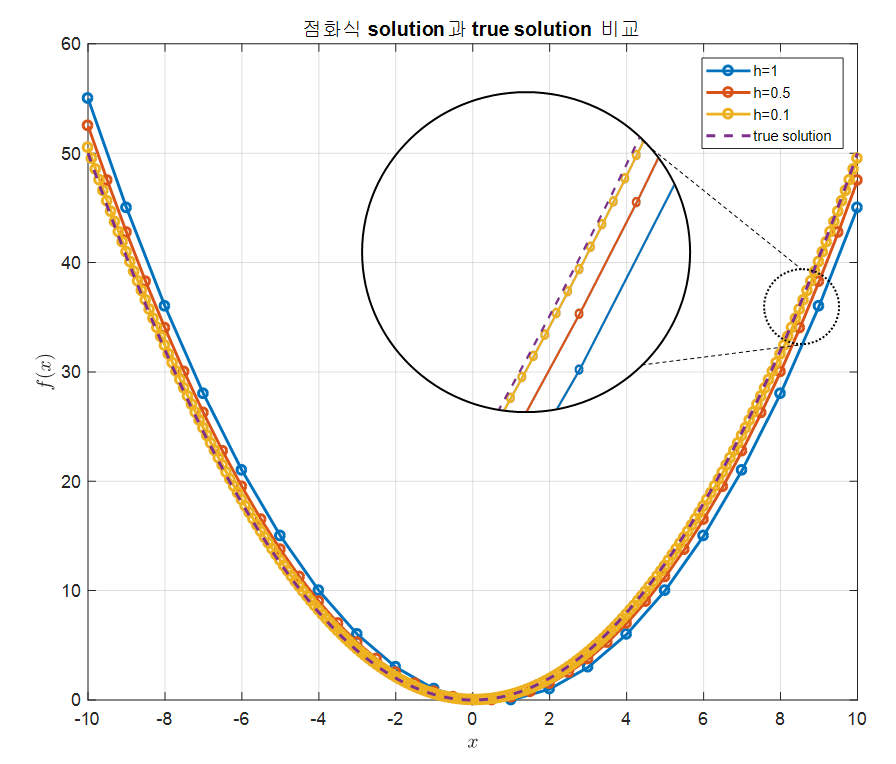
그림 6. 그림 2~4에서 표현된 점화식 solution과 true solution 간의 비교

그림 6를 보면 $h$의 값이 작을 수록 점화식으로 계산한 solution과 true solution은 비슷한 결과를 보여준다는 것을 알 수 있다.

정리하면,

위의 내용에서 step by step으로 설명한 방법이 오일러 방법이다¹.

그림 7. 오일러 방법에 대한 시각적 설명
그림 출처: 위키피디아: 오일러 방법

오일러 방법은 미분방정식을 수치해법으로 풀어주는 방법인데, 우리에게 몇 가지 점을 시사해준다.

1. 미분방정식의 solution을 구한다는 것은 미분방정식을 만족해주는 $f(x)$를 구하는 것이다.
2. 미분 방정식은 함수값의 변화에 대해 얘기해주고 있으며, 이것은 지금 포인트와 다음 포인트에서의 함수값 차이를 말해준다.
3. 시작점만 하나 특정할 수 있다면 미분방정식에서 말해주는 함수값 변화 룰에 따라 solution curve 하나를 구할 수 있다.
4. 지금 포인트와 다음 포인트 간의 간격이 좁을 수록 오일러 방법으로 예측한 solution curve는 true solution에 가까워진다.

초기값 문제

오일러 방법은 미분방정식이 함수값과 함수의 변화에 대한 관계를 설명한다는 사실에 기반한 solution 획득 방법이었다.

현재 함수값과 그 주변 함수값의 관계에 대해 알 수 있으므로, 어떤 한 점에서부터 바로 다음 정의역 값의 함수값을 추정해낼 수 있음을 알 수 있었다.

이렇게 매우 원시적인 미분방정식에 대한 해석을 이용한 것이 오일러 방법으로, 오일러 방법을 이용하면 주어진 미분방정식으로부터 함수값과 그 주변 함수값을 추정하여 솔루션을 찾아줄 수 있었다.

그러면, 지금까지 언급한 ‘현재 함수값’이란 것은 무엇일까?

생각해보면 여기서 언급되는 ‘현재 함수값’은 $(x, y)$ 평면 상의 어떤 점이어도 괜찮다. 내가 보고 있는 값이 무엇이든간에 상관없이 미분방정식의 solution을 생각할 수 있기 때문이다.

그리고, 미분방정식에 들어있는 ‘주변과의 관계’는 기울기로 표현될 수 있다. 미분계수의 기하학적의미가 기울기이기 때문이다.

즉, 미분 방정식을 이용하면 모든 $(x, y)$ 값에서 기울기를 그려줄 수 있다.

우리가 오일러 방법 편에서 그렸던 미분방정식인

\[\frac{dy}{dx}=x\]

에 대해 모든 점에서 기울기를 그리면 다음과 같다.

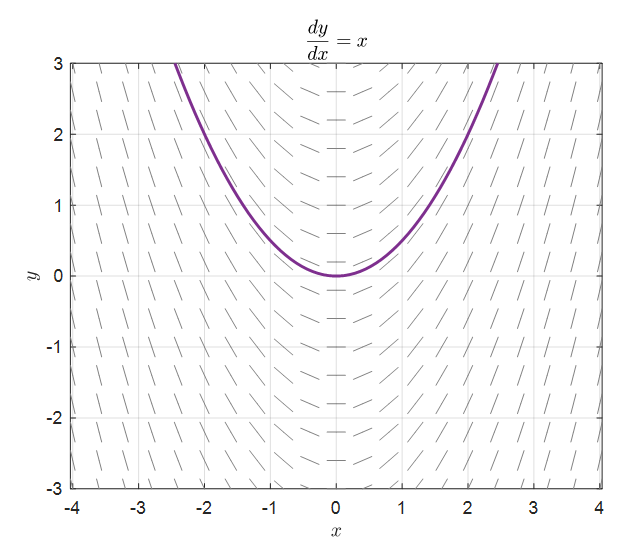
그림 8. dy/dx = x에 대한 기울기장과 솔루션 중 하나인 y = 1/2 * x^2

여기서 빨간색으로 그려진 막대기가 각 $(x, y)$ 좌표에서의 기울기를 뜻한다.

또 그림 8에서 보라색으로 칠해진 라인은 식 (2)의 솔루션 중 하나인 $y=1/2 x^2$을 의미한다.

여기서 생각해봐야 할 것은 그림 8의 보라색 라인은 $y(0) = 0$이라는 초기값에 따라 결정된 line이다.

만약 초기값이 다르다면 아래의 그림과 같이 다른 솔루션을 결과값으로 내줄 것이다.

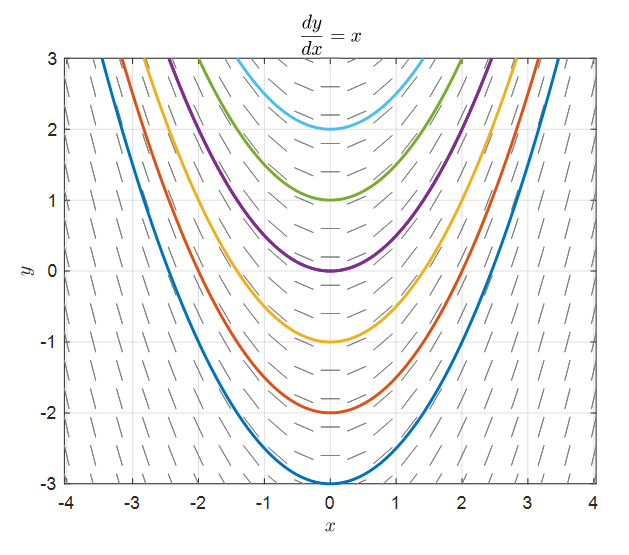
그림 9. 다양한 초기값에 대한 dy/dx = x에 대한 솔루션

다른 미분방정식의 방향장 확인

우리는 앞선 미분방정식을 이용한 현상 모델링 편에서 1계 미분방정식 모델을 두 가지 확인해보았다.

그것은 각각 Exponential growth와 logistic growth였다.

각각의 모델에 대한 방향장을 한번 확인해보도록 하자.

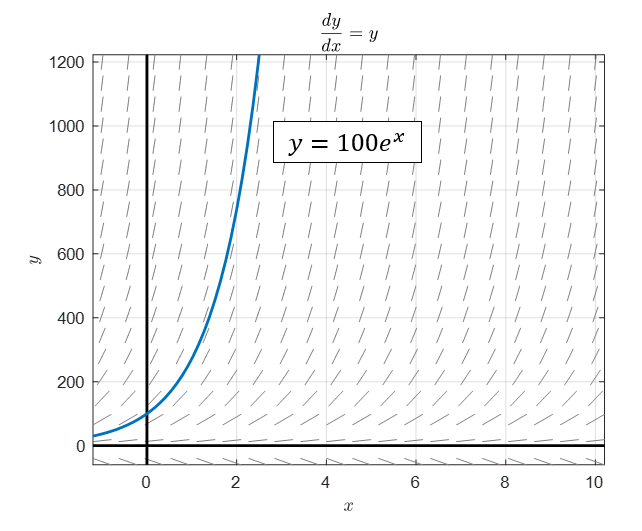
그림 10. Exponential growth model에 대한 방향장과 초기값이 100일 때의 솔루션ㄴ

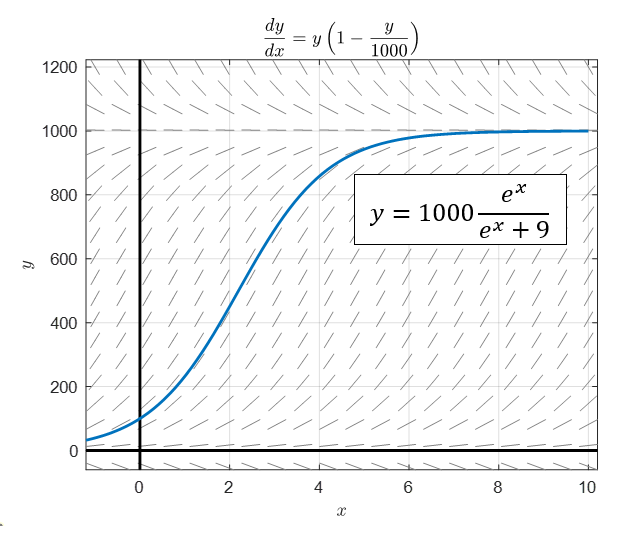
그림 11. logistic growth model에 대한 방향장과 초기값이 100일 때의 솔루션