주파수 샘플링과 DFT

주파수 샘플링 하는 목적에 대해서

우리는 지금까지 Analog Signal을 시간 영역에서 sampling 하여 Digital Signal로 변환시키고, Sample된 Digital Signal을 어떻게 하면 다시 Analog Signal로 원상 복구 시킬 수 있는지에 대해서 알아보았다. 이것은 일상생활에서 쉽게 접할 수 있는 아이디어로부터 출발하기 때문에 Nyquist Frequency Theorem이나 Ideal reconstruction의 개념은 그 필요성의 출발이 충분히 납득할 수 있는 것이었으리라 생각한다.

하지만 주파수는 왜 샘플링 하여야 하는가? 그것은 모든 Digital System은 이산화 되어 있기 때문이다. 즉, Discrete Time Signal을 이용하여, 또는 CT signal을 sample하여 그 신호의 주파수 응답을 분석해보는 것은 마치 컴퓨터에서 가능 할 것 처럼 보이지만, 실제로 분석하고자 하는 DT Signal이 주기신호가 아니라면 그것은 불가능하다. 그것은 DTFS와 DTFT가 정의된 수식에서 충분히 그 근거가 드러난다.

DEFINITION: Discrete Time Fourier Series (DTFS)
주기 이산 신호에 대하여, $$x[n] = \sum_{k=N_1}^{N_2}a_k \exp\left(j\frac{2\pi k}{N}n\right)$$ where $$a_k=\frac{1}{N}\sum_{n=N_1}^{N_2}x[n] \exp\left(-j\frac{2\pi k}{N}n\right)$$

DEFINITION: Discrete Time Fourier Transform (DTFT)
이산 신호에 대하여, $$x[n] = \int_{-0.5}^{0.5}X(f) \exp(j2\pi fn) df$$ where $$X(f)=\sum_{n=-\infty}^{\infty}x[n]\exp(-j2\pi fn)$$

다시 한번 DTFT의 수식을 살펴보면 $x[n]$ 과 $X(f)$ 모두 연속주파수 $f$ 를 가지고 있다는 것을 알 수 있다. 그렇기 때문에 컴퓨터를 이용해 일반적인 이산신호 $x[n]$ 의 주파수 응답을 알아보고 싶다면 연속 주파수 $f$ 를 샘플링하는 과정은 필연적인 것이다.

Sampling DTFT

우리는 연속주파수를 sample하기 전에 몇 가지 사실에 대해서 짚고 넘어가야 할 필요가 있다. 그것은 우리가 컴퓨터를 통해서 받는 신호는 any discrete time signal $x[n]$ 이라고 하지만, 어쨋든 길이가 유한할 수 밖에 없다. 그렇기 때문에 우리는 컴퓨터에서 사용할 일반적 이산신호 $x[n]$ 의 길이를 $N$ 으로 정하도록 하자. 그렇기 때문에 DTFT $X(f)$ 는 다음과 같이 생각될 수 있다.

\[\hat{X}(f)=\sum_{n=0}^{N-1}x[n]\exp(-j2\pi fn)\]

이제, 연속 주파수를 이산 주파수로 바꿔보자. CTFT와 DTFT의 유도과정을 다시 생각해보면 이렇게 바꿀 수 있다는 것을 금방 알 수 있을 것이다. 연속주파수 $f$는 $\lim_{N\rightarrow\infty}{\frac{k}{N}}$ 에서 출발했기 때문이다. 그러므로,

\[\hat{X}[k] = \sum_{n=0}^{N-1}x[n]\exp\left(-j\frac{2\pi k}{N}n\right)\]

이제, 위의 $\hat{X}[k]$ 를 새로운 푸리에 변환인 Discrete Fourier Transform이라고 정의할 수 있다.

DEFINITION: Discrete Fourier Transform (DFT)
전체 신호의 길이가 N인 이산 신호 $x[n]$ 에 대하여, $$X[k] = \sum_{n=0}^{N-1}x[n]\exp\left(-j\frac{2\pi k}{N}n\right)$$

이제, inverse Discrete Fourier Transform을 유도해보자. 지금껏 유도해왔던 Fourier Analysis Series와 마찬가지로 직교성(orthogonality)의 성질을 이용하면 된다.

PROOF inverse DFT의 유도

DFT는 아래와 같이 정의되었다.

\[X[k] = \sum_{n=0}^{N-1}x[n]\exp\left(-j\frac{2\pi k}{N}n\right)\]

두 정수 $p, n$ 에 대하여 다음과 같은 식을 생각하여 이산신호의 직교성의 성질을 이용하자.

\[\sum_{p=0}^{N-1}X[k] \exp\left(j\frac{2\pi p}{N}k\right)\] \[=\sum_{p=0}^{N-1} \sum_{n=0}^{N-1}x[n]\exp\left(-j\frac{2\pi k}{N}n\right) \exp\left(j\frac{2\pi p}{N}k\right)\] \[=\sum_{p=0}^{N-1}\sum_{n=0}^{N-1}x[n] \exp\left(j\frac{2\pi(p-n)}{N}k\right)\]

여기서도 CTFS에서 사용했던 방법과 마찬가지로 $p\neq n$, $p=n$ 의 두 가지 경우를 생각할 수 있다.

1) $p\neq n$인 경우,직교성의 성질에 의해

\[식(9) = \sum_{p=0}^{N-1}X[k] \exp\left(j\frac{2\pi p}{N}k\right) = 0\]

이고,

2) $p=n$인 경우 직교성의 성질에 의해

\[식(9) = \sum_{p=0}^{N-1}X[k] \exp\left(j\frac{2\pi p}{N}k\right) = Nx[n]\]

이다.

그러므로, inverse DFT는

\[x[n] = \frac{1}{N}\sum_{k=0}^{N-1}X[k] \exp\left(j\frac{2\pi k}{N}n\right)\]

이다.

DEFINITION: inverse Discrete Fourier Transform (iDFT)
전체 신호의 길이가 N인 이산 주파수 성분 $X[k]$ 에 대하여 $$x[n] = \frac{1}{N}\sum_{k=0}^{N-1}X[k] \exp\left(j\frac{2\pi k}{N}n\right)$$

예제를 통해 DFT를 조금 더 자세히 알아보자.

Ex) 다음의 이산신호 $x[n]$ 에 대하여 DFT $X[k]$ 를 구하시오.

\[x[n] = \begin{cases} 1, & n = 0, 1, 2, 3 \\ 0, & \text{otherwise} \end{cases}\]

Sol)

DFT의 정의에 따라,

\[X[k] = \sum_{n=0}^{3} 1 \times \exp\left(-j\frac{2\pi k}{4}n\right)\] \[= 1 + \exp\left(-j\frac{\pi}{2}k\right) + \exp\left(-j\pi k\right) + \exp\left(-j\frac{3\pi}{2}k\right)\]

그러므로, $k=0$ 일 때, $X[0]=4$ 이고, $k= 1,2,3$ 일 때, $X[k]=0$ 이다.

위와 같은 단순한 예제를 풂으로써 알 수 있는 것은 무엇일까? 바로 $x[n]$ 을 DTFT 한 결과물을 frequency domain에서 과연 sampling 했는지 알 수 있다는 것이다. 같은 문제를 가지고 DTFT를 구하면 다음과 같다.

ex2) 다음의 이산신호 $x[n]$ 에 대하여 DTFT $X(f)$ 를 구하시오.

\[x[n] = \begin{cases} 1, & n = 0, 1, 2, 3 \\ 0, & \text{otherwise} \end{cases}\]

Sol)

\[X(f) = \sum_{n=0}^{3}\left(1\times \exp({-j2\pi fn})\right)\] \[=\frac{1-\exp({-j8\pi f})}{1-\exp({-j2\pi f})}\]

여기서 위 식은 다음과 같이 변형할 수 있다.

\[= \frac {\frac{\exp({j4\pi f})-\exp({-j4\pi f})}{\exp({j4\pi f})}} {\frac{\exp({j\pi f})-\exp({-j\pi f})}{\exp({j\pi f})}}\] \[= \frac{\exp({j\pi f})}{\exp({j 4\pi f})} \times \frac{\exp({j 4\pi f}) - \exp({-j 4\pi f})}{\exp({j \pi f}) - \exp({-j \pi f})}\] \[=\exp\left(-j 3\pi f \right) \frac{\sin(4\pi f)}{\sin(\pi f)}\]

Ex2의 답의 결과에서 주파수 $f$를 $\frac{k}{4}$로 치환함으로써 주파수를 이산화해보자. 그렇게하면, 각각의 $k=0,1,2,3$ 에 대하여 Ex1의 결과와 같은 결과물을 얻게 된다는 것을 알 수 있다.

위 주파수의 이산화의 결과는 다음 그림을 통해서 확인해 볼 수 있다.

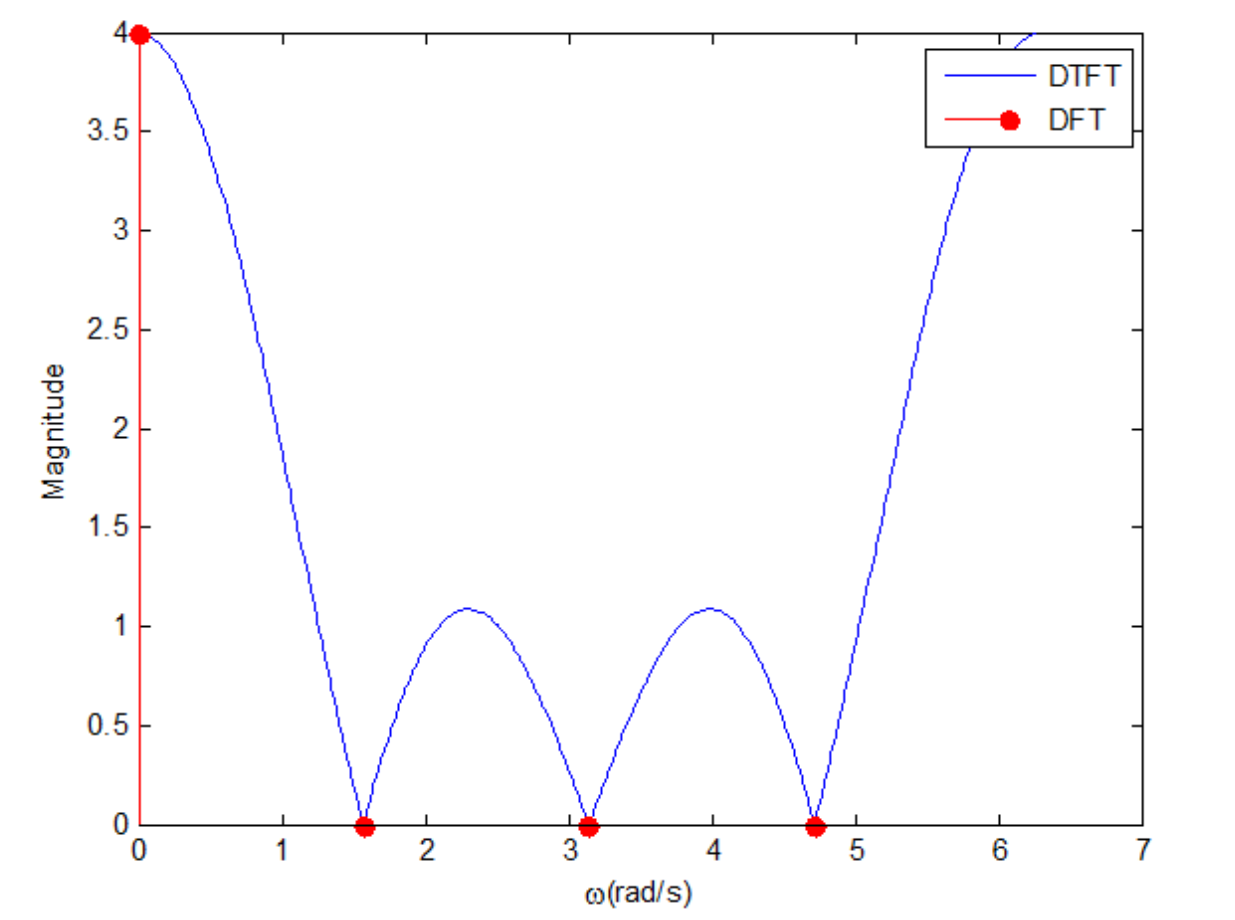
주파수 샘플링된 주파수 응답의 시간 영역에서의 표현

먼저, 시간을 샘플링 했을 때를 다시 생각해보자. 우리는 시간을 샘플링 했을 때에는 주파수 영역에서 주기성을 나타냈었다는 사실을 모두 증명했었다. 결과론적으로 얘기하자면, 시간과 주파수는 Dual Property를 가지고 있기 때문에, 주파수 영역에서 샘플링 한 신호는 시간 영역에서 주기성을 가지게 된다. $X(f)$의 연속 주파수 $f$ 를 $M$ 개로 Sampling한 신호를 $X_s[k]$ 라고 하자. 즉, $X_s[k]$ 는 이산 주파수 $f_k=\frac{k}{M}\space for \space k=0,1,\cdots,M-1$ 를 이용해서 표현될 수 있다. 이것은 Continuous Time Domain을 Sampling 할 때 이용한 기법을 이용해서 수학적으로 증명해 볼 수 있다.

\[X_s[k] = X\left(e^{j\frac{2\pi k}{M}}\right) = X(f) P(f)\] where \[P(f) = \frac{1}{M}\sum_{k=-\infty}^{\infty}\delta\left(f-\frac{k}{M}\right)\]

또한, 시간 샘플링 이론에서 증명되었던 것을 토대로 생각하면,

\[p[n] = \sum_{l=-\infty}^{\infty}\delta[n-lM]\]

또한, $X_s[k]=X(e^{j\frac{2\pi k}{M}})=X(f)P(f)$ 이므로, $x_s[n]=x[n]\otimes p[n]$ 이다.

그러므로,

\[x_s[n] = x[n] \otimes \sum_{l=-\infty}^{\infty} \delta[n-lM] = \sum_{l=-\infty}^{\infty} x[n]\otimes \delta[n-lM]\]

이것은 다음의 사실을 의미한다.

\[x_s[n] = \sum_{l=-\infty}^{\infty}x[n-lM]\]

즉, 위의 결과에 따르면 inverse DFT $x[n]$ 은 M을 주기로 하는 주기함수라는 것을 알 수 있다. 또한, Discrete Time Domain에서 표현되는 샘플의 갯수가 N인 $x[n]$ 의 aliasing을 방지하기 위해선 연속주파수를 sampling 할 때, $N\leq M$ 인 $M$ 개의 이산 주파수로 나눠야 한다는 것도 알 수 있다.

푸리에 행렬을 이용한 DFT의 이해

DFT를 이해하는 또 다른 방법은 신호를 벡터화 하고, 푸리에 변환은 푸리에 행렬을 통한 선형변환으로 보는 방법이다.

우선 DFT와 iDFT의 정의를 살펴보자.

DEFINITION: DFT and iDFT
전체 신호의 길이가 N인 이산 신호 $X[n]$과 길이가 N인 이산 주파수 성분 $X[k]$에 대하여 $$X[k] = \sum_{n=0}^{N-1}x[n]\exp\left(-j\frac{2\pi k}{N}n\right)$$ $$x[n] = \frac{1}{N}\sum_{k=0}^{N-1}X[k] \exp\left(j\frac{2\pi k}{N}n\right)$$

생각해보면 길이가 $N$인 신호 $x[n]$은 $N$차원 열벡터로 생각할 수 있으며, 여기에 마찬가지로 길이가 $N$인 이산 주파수 성분 $X[k]$역시 마찬가지로 $N$차원 열벡터로 생각할 수 있을 것이다.

즉, 신호는

\[\begin{bmatrix}x[0]\\ x[1] \\ \vdots \\ x[n] \\ \vdots \\ x[N-1]\end{bmatrix}\]

이고, 이를 적절시 선형변환 시켜 얻은 주파수 성분은

\[\begin{bmatrix}X[0]\\ X[1] \\ \vdots \\ X[k] \\ \vdots \\ X[N-1]\end{bmatrix}\]

와 같이 벡터화 시켜 생각해볼 수 있다. ($x[n]$과 $X[k]$의 대문자와 소문자 구별에 주의할 것.)

그렇다면 신호 벡터에 어떤 행렬(여기서 푸리에 행렬)을 통해 주파수 성분 벡터를 얻었다고 볼 수 있을 것이다. 이를 알기 위해 $k=0,1,\cdots, N-1$일 때의 $X[k]$ 값을 하나하나 계산해보자.

\[X[0] = x[0]\exp\left(-j\frac{2\pi 0}{N}0\right) + x[1]\exp\left(-j\frac{2\pi 0}{N}1\right)+\cdots +x[N-1]\exp\left(-j\frac{2\pi 0}{N}(N-1)\right)\] \[=x[0]\cdot 1 + x[1]\cdot 1 + \cdots + x[N-1] \cdot 1\] \[X[1] = x[0]\exp\left(-j\frac{2\pi 1}{N}0\right)+x[1]\exp\left(-j\frac{2\pi 1}{N}1\right)+x[N-1]\exp\left(-j\frac{2\pi 1}{N}(N-1)\right)\]

여기서 표기의 단순화를 위해

\[w = \exp\left(-j\frac{2\pi}{N}\right)\]

이라고 하자.

그러면,

\[\Rightarrow x[0]w^0 + x[1] w^1 + \cdots + x[n-1]w^{N-1}\]

이런 방식으로 $i$번째 주파수 성분 $X[i]$는 다음과 같이 계산할 수 있음을 알 수 있다.

\[X[i] = x[0]w^0 + x[1]w^{i\times1}+\cdots+x[j]w^{i\times j}+\cdots +x[n-1]w^{i\times(n-1)}\]

즉, 이런 과정을 거치게 되면 DFT를 다음과 같이 벡터와 행렬의 관계로 표현할 수 있다는 것을 알 수 있다.

\[\begin{bmatrix}X[0]\\X[1]\\ \vdots \\ X[N-1]\end{bmatrix} = \begin{bmatrix} 1 && 1 && 1 && \cdots && 1 \\ 1 && w^1 && w^2 && \cdots && w^{N-1} \\ 1 && \vdots && \vdots && \ddots && \vdots \\ 1 && w^{N-1} && w^{(N-1)\cdot 2} && \cdots && w^{(N-1)\cdot(N-1)}\end{bmatrix}\begin{bmatrix}x[0]\\x[1]\\ \vdots \\ x[N-1]\end{bmatrix}\]

행렬과 선형변환편에서는 행렬이 일종의 선형변환이라고 말했고,

행렬 곱에 대한 또 다른 시각편에서는 일반적인 행렬의 곱은 왼쪽에 곱해지는 행렬의 행과 오른쪽에 곱해지는 행렬의 한 열 간의 내적이라고 말한 바 있다.

또, 내적의 의미는 ‘닮음’이기도 한데, 그 말인 즉슨, 신호 벡터에 푸리에 행렬을 곱해준다는 것은 푸리에 행렬의 행과 신호 벡터가 얼마나 닮았는지를 확인해봄으로써 주파수 성분을 얻을 수 있다는 것을 말한다고 할 수 있다.

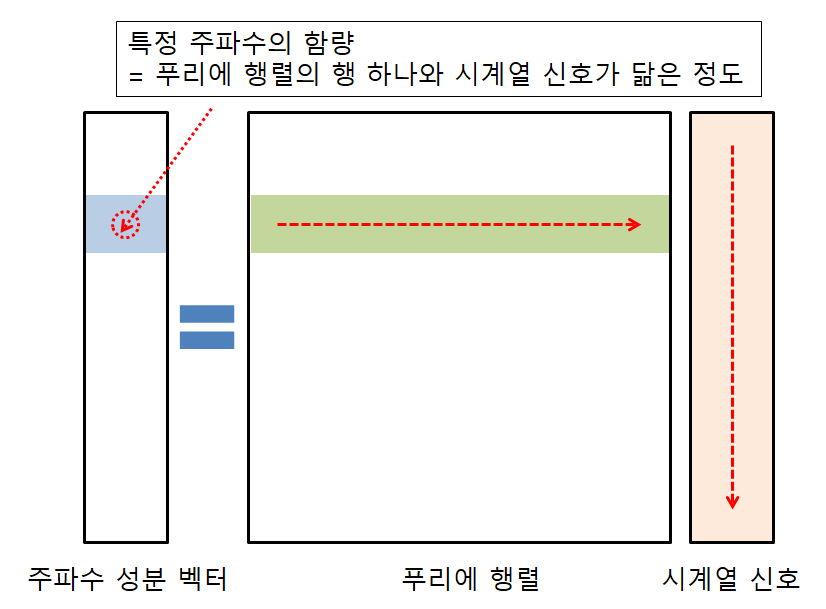
그림 2. 주파수 성분 벡터는 푸리에 행렬의 행과 시계열 벡터가 얼마나 닮았는지를 봄으로써 얻을 수 있는 것이다.

그렇다면, 푸리에 행렬의 각각의 행이 가져다주는 의미는 무엇일까?

푸리에 행렬이 가져다주는 의미

오일러 공식의 기하학적 의미편에서는 아래와 같은 공식의 의미에 대해 다룬 적이 있다.

\[e^{j\theta}=\cos(\theta) + j\sin(\theta)\]

식 (41)의 의미를 파악하기 위해 우변의 값을보면, 이는 복소평면에서 원점으로부터 $\theta$ 라디안만큼 회전한 호(弧, arc)의 좌표를 의미한다는 것을 알 수 있다.

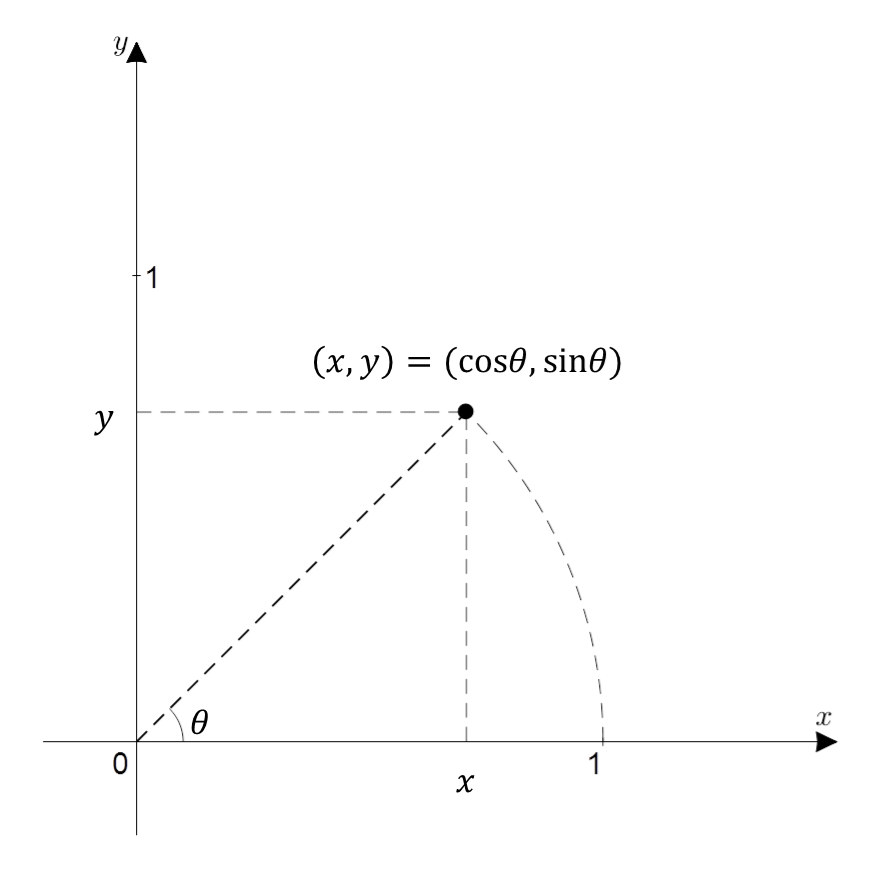
그림 3. 복소 평면 상에서 표현한 x+iy. 삼각함수로 표현하면 x축으로부터의 각도를 theta 라디안이라 했을 때 cos(theta) + i sin(theta)이다.

다시 말해 식 (40)에 있는 $w$는 다음과 같이 계산하는데,

\[w = \exp\left(-j\frac{2\pi}{N}\right)\]

이 말인 즉슨, 시계 방향으로 한 바퀴 도는 원 위의 점을 $N$ 등분 한 첫 번째 점의 위치라는 의미이다.

이와 같은 $w$의 의미를 생각하면서 $N=8$인 경우의 푸리에 행렬을 예시로 그 의미를 확인해보자.

$N=8$인 경우 푸리에 행렬에 들어가는 $w$의 값은 $w=\exp\left(-j\frac{2\pi}{8}\right)$이다. 이것을 복소평면에 표시하면 다음과 같다.

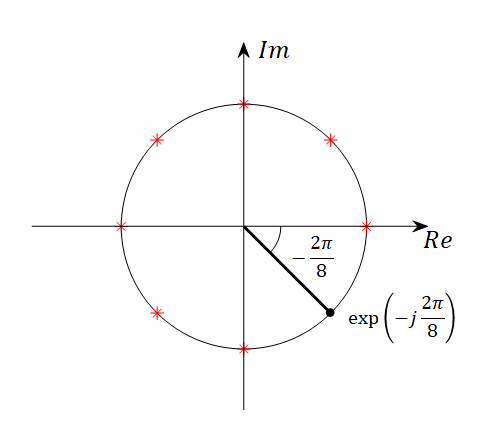
그림 4. $\exp(-j 2\pi/8)$을 복소평면 상에 표시한 것. 빨간색 별표는 w의 0승, 2승, 3승, ..., 7승을 표시한 것.

그림 4와 같이 $w$의 복소평면의 단위원 위의 phase로 푸리에 행렬 내의 복소수를 그림으로 대체하면 아래의 그림 5와 같을 것이다.

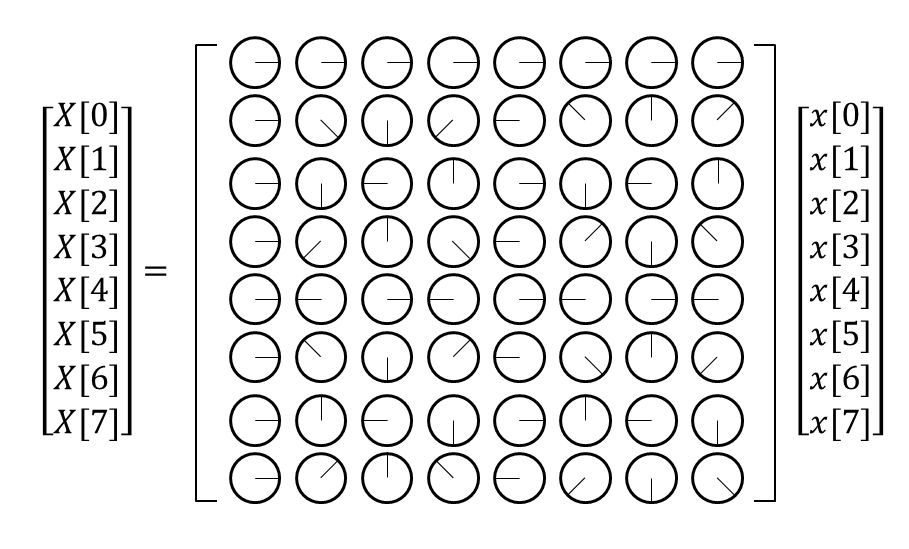
그림 5. $N=8$인 경우의 푸리에 행렬을 시각화 한 것. 푸리에 행렬 내의 그림은 복소수 $w$가 가르키는 phase를 표시하였다.

cosine 함수나 sine 함수 모두 원의 회전으로부터 출발하는 개념이므로 회전시 phase의 값은 모두 cosine 혹은 sine 함수의 값으로 바꿔 생각해볼 수 있다.

따라서 푸리에 행렬의 phase를 cosine 함수에 대해 생각해보면 다음과 같이 생각할 수 있다.

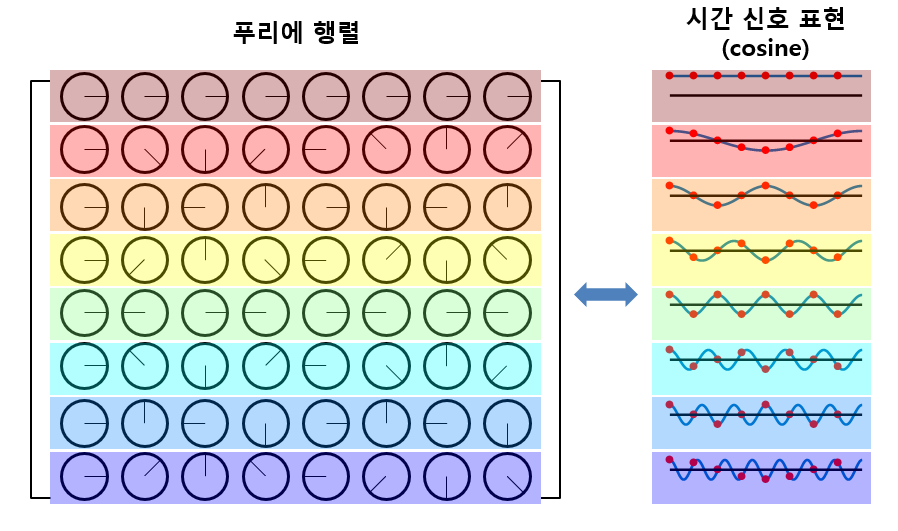
그림 6. 푸리에 행렬 내의 각 복소수 원소들의 phase를 sine 함수로 치환해 생각해본 경우

위의 그림 6에서 볼 수 있듯이 푸리에 행렬의 각 행은 주파수 0에서부터 fundamental frequency의 배수만큼의 cosine 함수를 표현하고 있는 것을 알 수 있다.

또, 푸리에 행렬의 phase를 sine 함수에 대해 생각해보면,

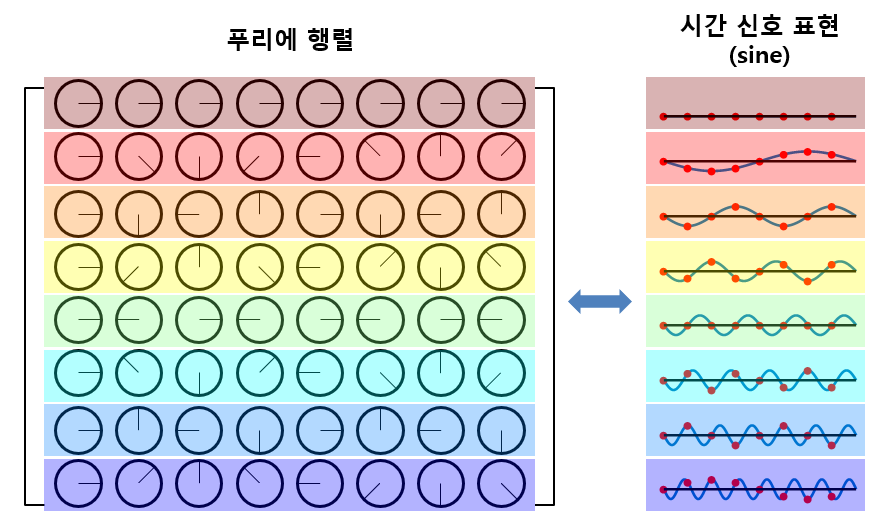
그림 7. 푸리에 행렬 내의 각 복소수 원소들의 phase를 sine 함수로 치환해 생각해본 경우

위의 그림 7에서 볼 수 있듯이 푸리에 행렬의 각 행은 주파수 0에서부터 fundamental frequency의 배수만큼의 sine 함수도 함께 표현하고 있는 것을 알 수 있다.

즉, DFT를 계산할 때 사용하는 푸리에 행렬은 fundamental frequency의 배수로 구성된 cosine, sine 함수들이며, 이 함수들이 실수부와 허수부를 구성하며, 원래의 시간 신호와 하나 하나 내적되어 결과를 얻어주는 것이다.

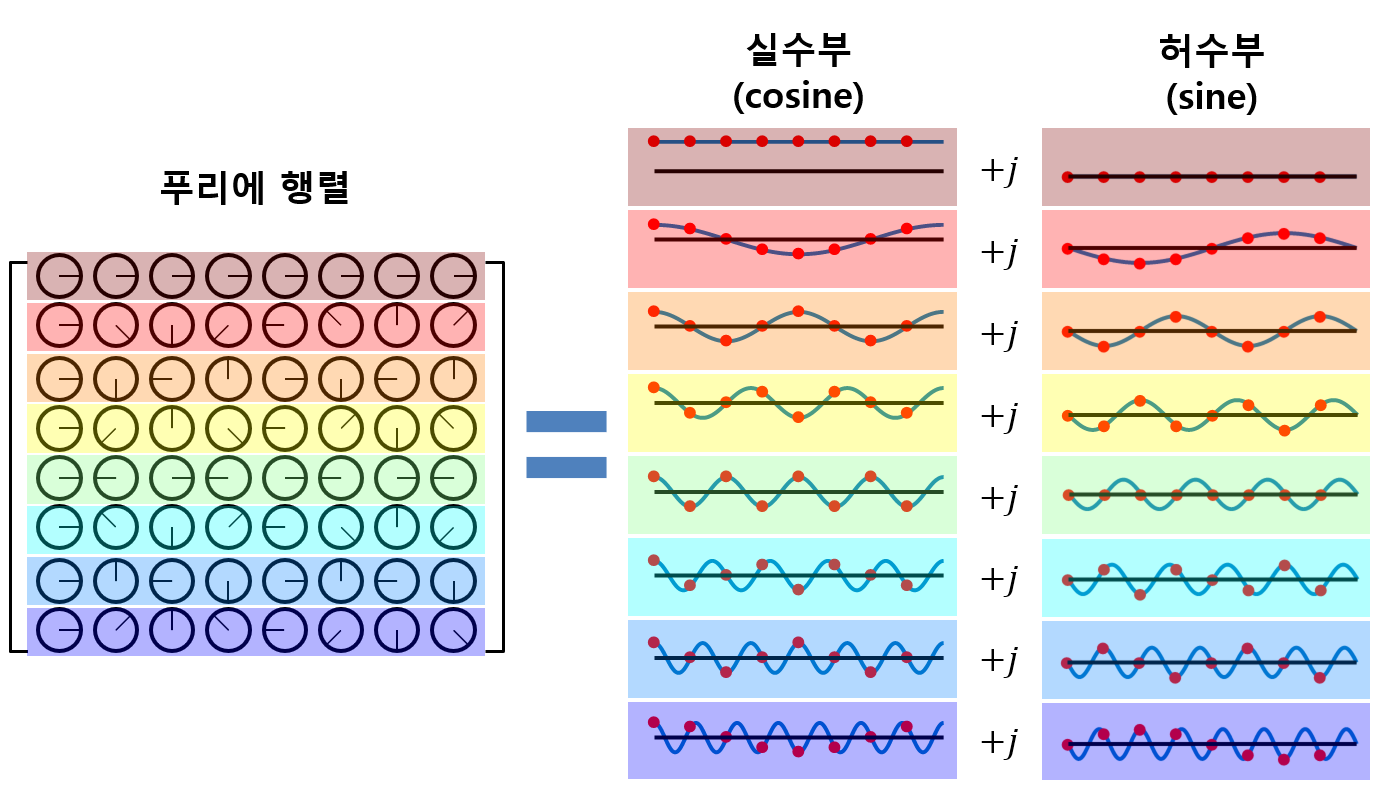
그림 8. 푸리에 행렬 내의 값들은 모두 복소수이며, 실수부와 허수부는 각각 cosine, sine 함수로 구성되어 있다는 것을 알 수 있다.

푸리에 행렬의 특성

이번에는 푸리에 행렬의 특성을 파악해보자.

1. 푸리에 행렬의 열들은 서로 직교함

우리는 간단한 방법으로 푸리에 행렬의 각 열들이 직교한다는 것을 확인할 수 있다.

가장 쉬운 방법으로는 푸리에 행렬 $F$에 Hermitian 연산¹을 취한 뒤 곱해보는 것이다.

즉,

\[F^HF = \begin{bmatrix} 1 && 1 && 1 && \cdots && 1 \\ 1 && w^{*1} && w^{*2} && \cdots && w^{*(N-1)} \\ 1 && \vdots && \vdots && \ddots && \vdots \\ 1 && w^{*(N-1)} && w^{*(N-1)\cdot 2} && \cdots && w^{*(N-1)\cdot(N-1)}\end{bmatrix} \begin{bmatrix} 1 && 1 && 1 && \cdots && 1 \\ 1 && w^1 && w^2 && \cdots && w^{N-1} \\ 1 && \vdots && \vdots && \ddots && \vdots \\ 1 && w^{N-1} && w^{(N-1)\cdot 2} && \cdots && w^{(N-1)\cdot(N-1)}\end{bmatrix}\] \[=N\begin{bmatrix}1 && 0 && \cdots && 0 \\ 0 && 1 && \cdots && 0 \\ \vdots && \vdots && \ddots && \vdots \\ 0 && 0 && \cdots && 1\end{bmatrix} = N\cdot I\]

여기서 superscript ‘*‘은 complex conjugate이다.

식 (44)의 결과와 같이 푸리에 행렬 $F$의 각 열들은 각 열 자신과 내적 시에는 $N$이라는 값을 갖고 이외의 열과 내적했을 때는 0이라는 결과를 얻어주게 되므로, 각각의 열들은 서로 직교한다는 것을 알 수 있다.

2. 푸리에 행렬의 역행렬과 역푸리에 변환

또, 식 (43)과 식 (44)를 통해 푸리에 행렬의 역행렬은

\[F^{-1}=\frac{1}{N}F^H\]

라는 것을 알 수 있다.

즉,

\[\begin{bmatrix}x[0]\\x[1]\\ \vdots \\ x[n-1]\end{bmatrix} = \frac{1}{N}\begin{bmatrix} 1 && 1 && 1 && \cdots && 1 \\ 1 && w^{*1} && w^{*2} && \cdots && w^{*(N-1)} \\ 1 && \vdots && \vdots && \ddots && \vdots \\ 1 && w^{*(N-1)} && w^{*(N-1)\cdot 2} && \cdots && w^{*(N-1)\cdot(N-1)}\end{bmatrix}\begin{bmatrix}X[0]\\X[1]\\ \vdots \\ X[N-1]\end{bmatrix}\]

이며, 이것은 inverse DFT의 식과 같다는 것 또한 쉽게 알 수 있을 것이다.

3. 역 푸리에 변환이 말해주는 것

행렬 곱에 대한 새로운 시각 편에서 열공간에 기반한 해석 파트를 다시 한번 생각해보자.

예를 들어 아래와 같은 행렬은,

\[\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}3\\5\end{bmatrix}\]

연립방정식을 풀면 쉽게 알 수 있다.

\[\begin{cases} x+2y = 3 \\ 3x+4y = 5 \end{cases}\] \[\Rightarrow x=-1, \text{ }y=2\]

하지만, 이번엔 이 식을 아래와 같이 생각해보자.

\[x\begin{bmatrix}1\\3\end{bmatrix}+y\begin{bmatrix}2\\4\end{bmatrix}=\begin{bmatrix}3\\5\end{bmatrix}\]

위 식에 대한 해석은 아래와 같이 할 수도 있다고 행렬 곱에 대한 새로운 시각 편에서 언급한 바가 있다.

"두 벡터 $\begin{bmatrix}1\\3\end{bmatrix}$과 $\begin{bmatrix}2\\4\end{bmatrix}$로부터 생성된 벡터공간 내에 벡터 $\begin{bmatrix}3\\5\end{bmatrix}$가 존재하는가? 만약 그렇다면, $\begin{bmatrix}1\\3\end{bmatrix}$과 $\begin{bmatrix}2\\4\end{bmatrix}$을 어떻게 조합해야 $\begin{bmatrix}3\\5\end{bmatrix}$을 구할 수 있을까??"

이 얘기를 푸리에 행렬에 그대로 적용해본다면 우리가 역 푸리에 변환을 취해준다는 것의 의미는 다음과 같다.

“N개의 $F^{-1}$의 열벡터로 생성된 벡터 공간 내에 $N$ 차원 시계열 벡터가 존재하는가?”

“그렇다면 $F^{-1}$의 열벡터를 어떻게 조합해야 시계열 벡터를 만들 수 있는가?”

즉, 무슨 말인가?

즉, 모든 시계열들은 정현파의 합으로 구성할 수 있으며, 정현파를 어떻게 조합하는가에 따라 시계열의 형태가 달라진다는 것을 다시 한번 방증하는 것이다.