Gradient Descent 방법은 1차 미분계수를 이용해 함수의 최소값을 찾아가는 iterative한 방법이다.
Step size를 조정해가며 최소값을 찾아가는 과정을 관찰해보자.

gradient descent 방법의 직관적 의미

gradient descent 방법은 steepest descent 방법이라고도 불리는데, 함수 값이 낮아지는 방향으로 독립 변수 값을 변형시켜가면서 최종적으로는 최소 함수 값을 갖도록 하는 독립 변수 값을 찾는 방법이다.

steepest descent 방법은 다음과 같이 많이 비유되기도 한다.

앞이 보이지 않는 안개가 낀 산을 내려올 때는 모든 방향으로 산을 더듬어가며 산의 높이가 가장 낮아지는 방향으로 한 발씩 내딛어갈 수 있다.

gradient descent의 목적과 사용 이유

gradient descent는 함수의 최소값을 찾는 문제에서 활용된다.

함수의 최소, 최댓값을 찾으려면 “미분계수가 0인 지점을 찾으면 되지 않느냐?”라고 물을 수 있는데,

미분계수가 0인 지점을 찾는 방식이 아닌 gradient descent를 이용해 함수의 최소값을 찾는 주된 이유는

• 우리가 주로 실제 분석에서 맞딱드리게 되는 함수들은 닫힌 형태(closed form)가 아니거나 함수의 형태가 복잡해 (가령, 비선형함수) 미분계수와 그 근을 계산하기 어려운 경우가 많고,
• 실제 미분계수를 계산하는 과정을 컴퓨터로 구현하는 것에 비해 gradient descent는 컴퓨터로 비교적 쉽게 구현할 수 있기 때문이다.

추가적으로,

• 데이터 양이 매우 큰 경우 gradient descent와 같은 iterative한 방법을 통해 해를 구하면 계산량 측면에서 더 효율적으로 해를 구할 수 있다.

gradient descent의 수식 유도

gradient descent는 함수의 기울기(즉, gradient)를 이용해 $x$의 값을 어디로 옮겼을 때 함수가 최소값을 찾는지 알아보는 방법이라고 할 수 있다.

기울기가 양수라는 것은 $x$ 값이 커질 수록 함수 값이 커진다는 것을 의미하고, 반대로 기울기가 음수라면 $x$값이 커질 수록 함수의 값이 작아진다는 것을 의미한다고 볼 수 있다.

또, 기울기의 값이 크다는 것은 가파르다는 것을 의미하기도 하지만, 또 한편으로는 $x$의 위치가 최소값/최댓값에 해당되는 $x$ 좌표로부터 멀리 떨어져있는 것을 의미하기도 한다.

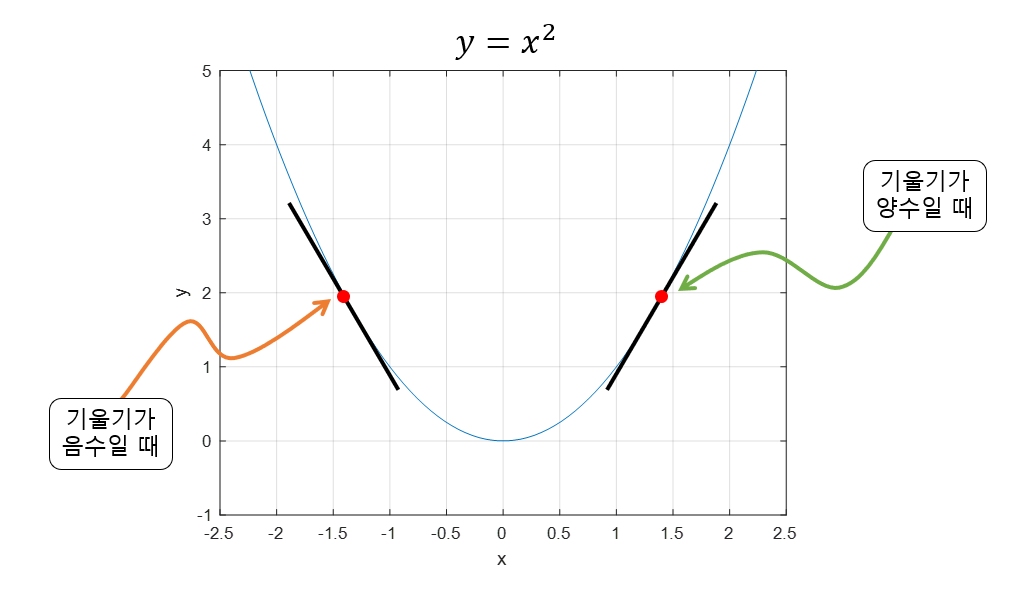
그림 1. 기울기가 양수일 때와 음수일 때의 비교

gradient의 방향 성분을 이용하자.

이를 이용해 특정 포인트 $x$에서 $x$가 커질 수록 함수값이 커지는 중이라면 (즉, 기울기의 부호는 양수) 음의 방향으로 $x$를 옮겨야 할 것이고,

반대로 특정 포인트 $x$에서 $x$가 커질 수록 함수값이 작아지는 중이라면 (즉, 기울기의 부호는 음수) 양의 방향으로 $x$를 옮기면 된다.

이 논리를 수식으로 쓰면 다음과 같다.

\[x_{i+1} = x_i - \text{이동 거리}\times\text{기울기의 부호}\]

여기서 $x_{i}$와 $x_{i+1}$은 각각 $i$번째 계산된 $x$의 좌표와 $i+1$번째 계산된 $x$의 좌표를 의미한다.

그러면 여기서 이동거리는 어떻게 생각해야 할까? 그것은 gradient의 크기를 이용하면 된다.

gradient의 크기도 이용해보자.

식 (1)의 문제점을 생각해보면 “이동 거리”라는 factor를 어떻게 구할지 생각해보아야 한다는 점이다.

이 문제에 대해 다시 잘 생각해보면 미분 계수(즉, 기울기 혹은 gradient)값은 극소값에 가까울 수록 그 값이 작아진다.

사실 극대값에 가까울 때에도 미분 계수는 작아지기 마련인데, gradient descent 과정에서 극대값에 머물러 있는 경우는 극히 드물기 때문에 이 문제에 대해서는 고려하지 않고자 한다.

따라서, 이동거리에 사용할 값을 gradient의 크기와 비례하는 factor를 이용하면 현재 $x$의 값이 극소값에서 멀 때는 많이 이동하고, 극소값에 가까워졌을 때는 조금씩 이동할 수 있게 된다.

즉, 이동거리 는 gradient 값을 직접 이용하되, 이동 거리를 적절히 사용자가 조절 할 수 있게 수식을 조정해 줌으로써 상황에 맞게 이동거리를 맞춰나갈 수 있게 하면 될 것이다.

이 때, 이동 거리의 조정 값을 보통 step size라고 부르고 기호는 $\alpha$로 쓰도록 하겠다.

따라서 최종 수식은 다음과 같이 계산할 수 있다.

최종 수식

최적화하고자 하는 함수 $f(x)$에 대해 다음과 같이 쓸 수 있다.

\[x_{i+1} = x_i - \alpha \frac{df}{dx}(x_i)\]

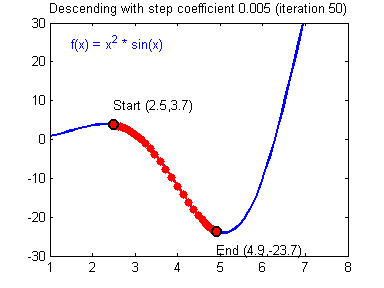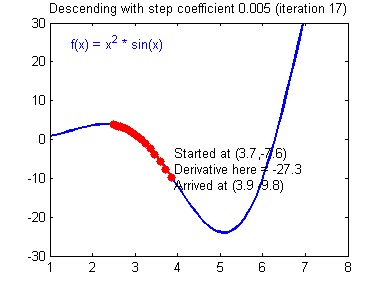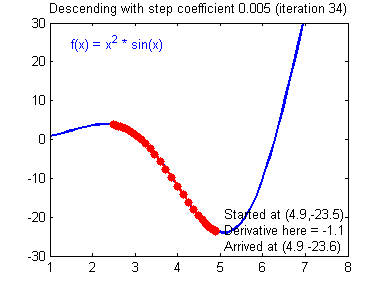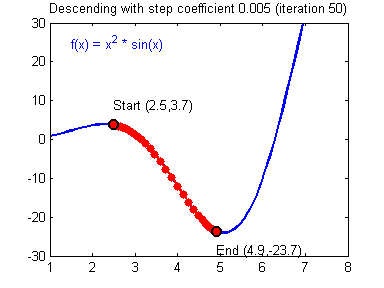
그림 2. 함수 $f(x)$에 대한 gradient descent의 시각화
그림 출처

이를 다변수함수에 대해 확장하면 다음과 같이 쓸 수 있다.

\[x_{i+1} = x_i - \alpha \nabla f(x_i)\]

아래는 변수가 두 개인 경우에 대한 gradient descent의 예시 장면으로, 선형 회귀 모델을 찾는 과정이다.

아래의 그림 3의 오른쪽의 contour plot이 등고선을 의미한다고 보면 된다.

그림 3. 경사하강법(gradient descent)을 이용해 비용함수의 최솟값을 찾는 과정
※ 비용 함수의 parameter들은 모두 normalize하여 시각화하였음.

적절한 크기의 step size

step size가 큰 경우 한 번 이동하는 거리가 커지므로 빠르게 수렴할 수 있다는 장점이 있다. 하지만, step size를 너무 크게 설정해버리면 최소값을 계산하도록 수렴하지 못하고 함수 값이 계속 커지는 방향으로 최적화가 진행될 수 있다.

또, 한편 step size가 너무 작은 경우 발산하지는 않을 수 있지만 최적의 $x$를 구하는데 소요되는 시간이 오래 걸린다는 단점이 있다.

아래의 그림을 통해 적절한 step size를 선택하지 못하는 경우 수렴하지 않거나 발산하는 경우를 확인해볼 수 있다.

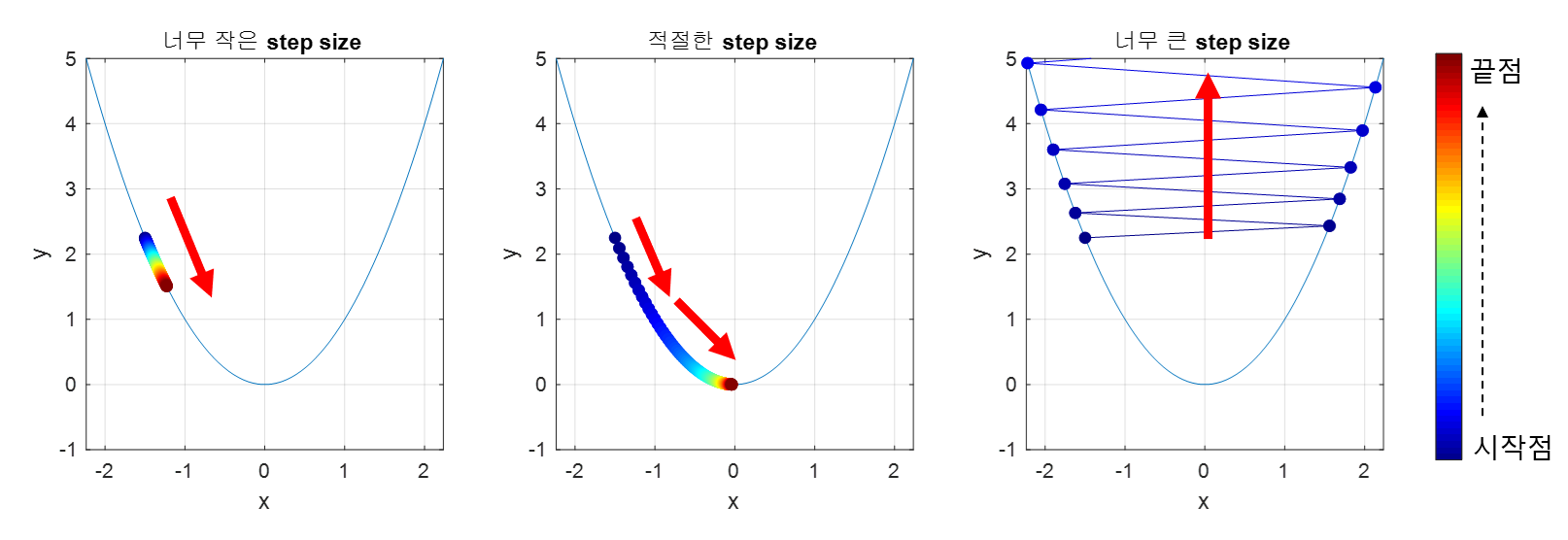
그림 4. step size가 너무 작으면 매 step 별로 이동하는 거리가 너무 작아 수렴하지 못하고, step size가 너무 크면 발산하게 될 수 있다.

local minima 문제

Gradient descent의 또 다른 문제는 local minima 문제이다. 실제로 우리가 찾고 싶은 것은 아래의 그림에서 볼 수 있는 빨간점이 표시하는 global minimum이지만,

gradient descent 알고리즘을 시작하는 위치는 매번 랜덤하기 때문에 어떤 경우에는 local minima에 빠져 계속 헤어나오지 못하는 경우도 생긴다.

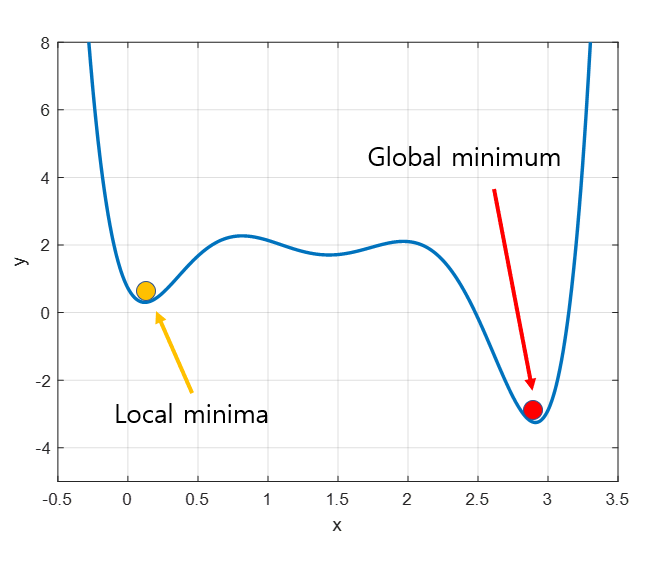
그림 5. 실제로 얻고 싶은 값은 global minimum(빨간색)이지만, initialization이 우연히도 잘못 되면 local minima(노란색)에 빠지기도 한다.