Divergence와 Curl은 벡터장에서 적용되는 연산자인데 우선 벡터장(vector field)이란 유클리드 공간의 각 점에 벡터를 대응시킨 것이라고 할 수 있다.
유체의 흐름, 중력장 등 각 점에서의 크기와 방향을 나타내기 위해 사용한다. (위키피디아, 벡터장)
Divergence (발산)
Divergence는 벡터장 내에서 임의의 한 점 $(x,y)$의 매우 작은 공간 안에서 벡터장이 퍼져 나오는지 아니면 모여서 없어지는지의 정도를 측정하는 연산자이다.
부족하지만 내 생각으로는 해당 임의의 점 $(x,y)$에서 벡터장이 향하는 방향으로의 정규화시킨 변화량을 확인한 것이라고도 생각할 수 있을 것 같다.
또, 물리적으로 벡터장의 발산이 의미하는 것은 매우 작은 공간(미소 면적, 혹은 미소 부피)에서 빠져나가거나 들어가며 변하는 단위 부피 당 유량이라고 할 수 있다.
매우 작은 공간 안에서 벡터장이 퍼져 나오는지를 확인해보기 전에 조금 더 macro 스케일에서 벡터장이 나오는지 모여서 없어지는 지를 한번 확인해보자.
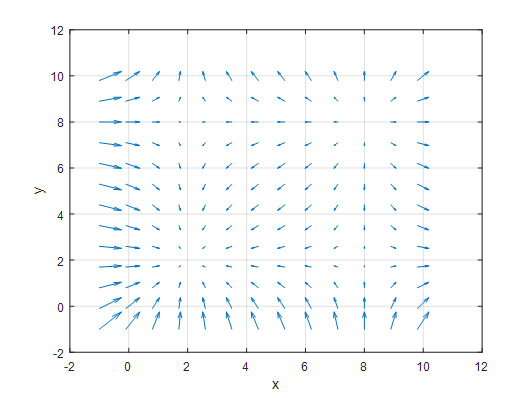
그림 1. xy 평면에서 모이기도 하고 나오기도 하는 점이 있는 벡터장
위와 같이 xy 평면상에 벡터장이 있다고 생각해보자. 얼핏 보기에 (2,2), (2,8), (8,2), (8,8)에서 벡터장이 모여서 사라지거나 퍼져 나오는 점이 있다는 것을 알 수 있을 것이다.
그렇다면 macro level에서는 임의의 점 에서 발산량을 확인하려면 어떤식으로 생각해야 할까? 일반적으로는 아래와 같이 생각할 수 있을 것이다.
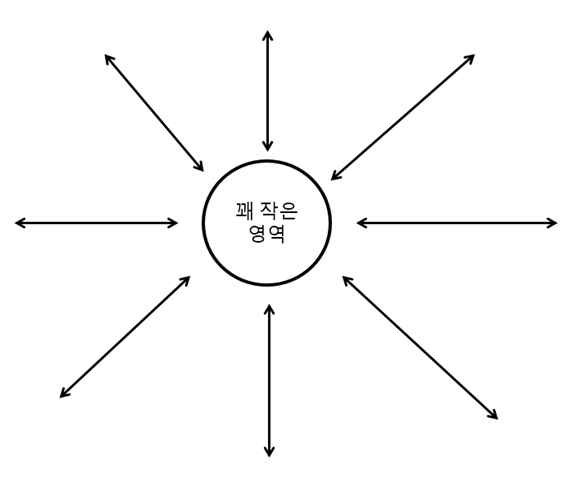
그림 2 macro level에서 생각한 발산량을 생각하는 방법
그런데 이렇게 발산량을 정의하려면 생각해야 할 문제가 있다.
가장 큰 문제는 실제로는 그림 2에 표현된 화살표는 벡터장 내의 벡터를 몇 개 샘플링해서 보여준 것이고 실제로는 매우 빽빽하게 많은 벡터들이 ‘꽤 작은 영역’으로 들어오거나 나가기 때문이다.
그렇기 때문에 발산량을 생각할 때는 미소 영역에서 벡터의 발산량을 생각해주어야 한다.
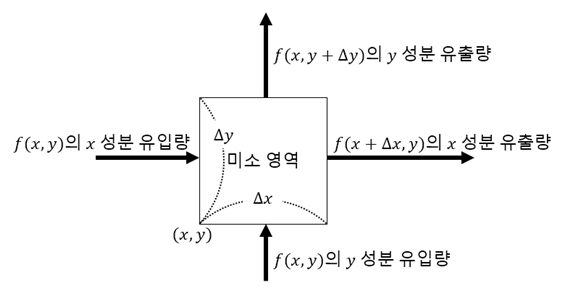
그림 3 미소 영역에서 확인할 수 있는 벡터장의 발산량
미소 영역에서만 벡터장의 유입, 유출량의 차이만을 생각하게 되면 두 방향으로부터만 들어오거나 나가는 벡터만 생각해줄 수 있다. 극한의 영역이기 때문이다.
그렇다면 이 미소 영역에서의 벡터 발산량은 어떻게 확인할 수 있을까?
그것은 (유출량 – 유입량)이다. 물론 $x$축에서의 발산량과 $y$축에서의 발산량을 합쳐야 한다.
그렇다면 벡터 함수 $f(x,y)$를 $f(x,y)=P(x,y)\hat{i}+Q(x,y)\hat{j}$로 정의했을 때, 미소 영역에서의 발산량은 다음과 같이 정의될 것이다.
미소 영역의 발산량 = $x$ 성분 방향의 발산량 + $y$ 성분 방향의 발산량
\[= \lim_{\Delta x\rightarrow 0}\lim_{\Delta y\rightarrow 0} \left\{ \frac{P(x+\Delta x, y+\frac{1}{2}\Delta y) - P(x, y+\frac{1}{2}\Delta y)}{\Delta x} + \frac{Q(x+\frac{1}{2}\Delta x, y+\Delta y) - Q(x+\frac{1}{2}\Delta x, y)}{\Delta y} \right\}\]$\Delta x$와 $\Delta y$로 나눠주는 것은 해당 미소 영역의 너비와 높이에 맞게 정규화 시켜준 것이라고 생각해도 될 것 같다.
그렇다면 이 미소 영역의 발산량은 편미분의 정의를 통해 다음과 같이 나타낼 수 있다.
\[\text{미소 영역의 발산량} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y}\]한편, 스칼라 필드와 Gradient편을 보았다면 Del 연산자를 보았을 텐데, 복습하는 차원에서 한 번 더 적어보자면 스칼라 함수 (또는 필드) 의 gradient는 다음과 같이 적었다.
\[gradient(f) = \nabla f=\frac{\partial}{\partial x}f(x,y)\hat{i} + \frac{\partial}{\partial y}f(x,y)\hat{j}\]여기서 $\nabla$연산자만 다음과 같이 떼서 생각해볼 수 있다.
\[\nabla = \frac{\partial}{\partial x}\hat{i} +\frac{\partial}{\partial y}\hat{j}\]벡터의 divergence(발산)는 내가 생각하는 정의에 따르면 벡터장이 향하는 방향으로의 변화량을 확인하는 것이기 때문에 $\nabla$과 벡터장 $f(x,y)$를 내적함으로써 얻는 다고도 생각할 수 있을 것 같다.
벡터장 $f(x,y)$를 $P(x,y)\hat{i}+Q(x,y)\hat{j}$라 하자. 벡터장 $f$의 divergence는 다음과 같이 계산할 수 있다.
\[\nabla \cdot f = \left(\frac{\partial }{\partial x}\hat{i} + \frac{\partial }{\partial y}\hat{j}\right)\cdot\left(P(x,y)\hat{i} + Q(x,y)\hat{j}\right) = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y}\]이것은 앞에서 구한 미소 영역의 발산량과 동일하다.
한 가지만 덧붙이자면 발산(divergence)은 벡터장에 적용해서 임의의 점 $(x,y)$에서 스칼라 값을 얻게 된다.
Divergence의 예시
이제, 예를 들어 보기 위해 다음과 같은 벡터장을 생각해보자.
\[f(x,y) = 2x\hat{i} + (0)\hat{j}\]그러니까 x 축에서 값이 양수로 갈수록 벡터의 크기는 커지는데 방향은 여전히 오른쪽을 향하게 되는 벡터장이다. MATLAB으로 그리면 다음과 같다.
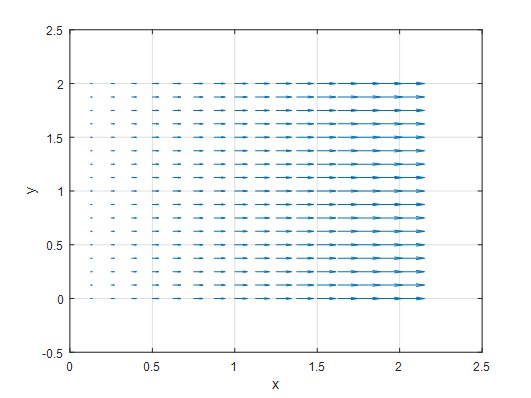
그림 4 벡터장 $f(x,y)=2x\hat{i}$를 표시한 그림
그렇다면 이러한 벡터장에서 divergence는 무엇을 의미할까? 우선 divergence를 구해보면
\[\nabla \cdot f = \frac{\partial (2x)}{\partial x} + \frac{\partial(0)}{\partial y} = 2\]$xy$ 평면 상의 어떤 점이든지 상관없이 이 벡터장의 divergence는 항상 2이다. 이것이 의미하는 바는 무엇일까?
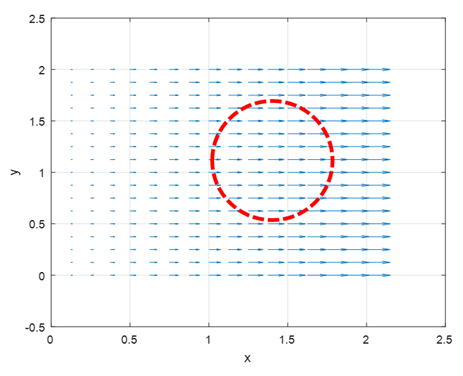
그림 5 벡터장 위에 임의의 구역을 설정해보자. 빨간색으로 임의의 구역을 표시했다. 임의의 구역 내에 들어가고 나오는 벡터들의 net sum(순(純) 합)은 어떻게 되는가?
그림 5를 보도록 하자. 같은 벡터장 $f(x,y)=2x\hat{i}$를 그린 것인데 그 위에 임의의 영역을 빨간색 동그라미로 그려보았다. 이 동그라미 안에 들어가고 나오는 벡터들이 있다는 것을 알 수 있을 것이다.
그렇다면 이 때 들어가고 나오는 벡터의 순 합(net sum, 純合)은 양의 값이다.
이 때 동그라미가 매우 매우 작아져서 미소 면적에 가까워 졌을 때, 정규화시킨 벡터의 순 합의 변화값은 2라는 것이다.
즉, 2라는 속도의 변화량을 가지고 벡터장의 순합이 변하게 된다는 뜻이다.
divergence는 가령 속도 벡터가 있는 벡터장에 적용했을 때 각 임의의 점 $(x,y)$ 에서의 가속도를 얻는 것이라고 할 수 있을 것 같다.
이번에는 그림 1의 벡터장의 divergence를 확인해보자.
그림 1의 벡터장은 다음과 같은 벡터 함수이다.
\[f(x,y) = (x-2)(x-8)\hat{i} + (y-2)(y-8)\hat{j}\]divergence를 구해보면
\[\nabla \cdot f = 2x-10+2y-10 = 2x+2y-20\]가 된다.
즉, $y=-x+10$이라는 선을 기준으로 그 위는 divergence 값이 양수이고 그 아래로는 divergence 값이 음수가 될 것이다.
MATLAB으로 확인해보면 다음과 같다. 계산한 값과 정확히 일치하는 결과를 확인할 수 있다.
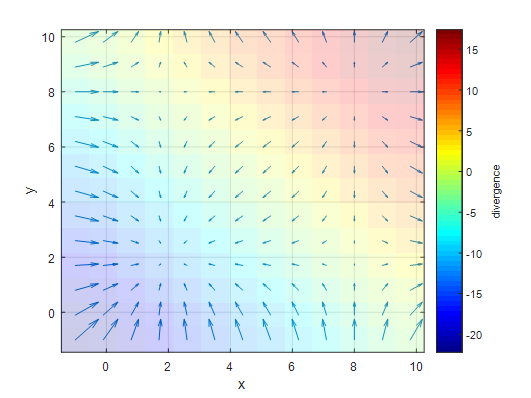
그림 6 $f(x)=(x-2)(x-8)\hat{i}+(y-2)(y-8)\hat{j}$ 의 divergence를 확인한 plot. $y=-x+10$을 중심으로 그 위는 양의 divergence, 그 아래로는 음의 divergence 값을 가진다.
※ MATLAB 코드는 공돌이의 수학정리노트 Github Repo에서 받으실 수 있습니다.
$\Rightarrow$ 공돌이의 수학정리노트 Github Repo