힐버트 변환이 필요한 이유

힐버트 변환이 필요한 이유에 대해 설명하기 위해서는 힐버트 변환이 하는 역할이 무엇인지, 그리고 그 역할을 수행함으로써 얻을 수 있는 결과는 무엇인지 파악하는 것이 중요한 과정일 것이라는 생각이 든다. 먼저, 힐버트 변환의 역할은 일종의 선형 필터로써 신호의 amplitude는 유지하되, phase만 $-\frac{\pi}{2}$만큼 shift 시켜주는 것이다. (음의 주파수의 경우에는 $\pi/2$만큼 phase shift 시켜준다.)

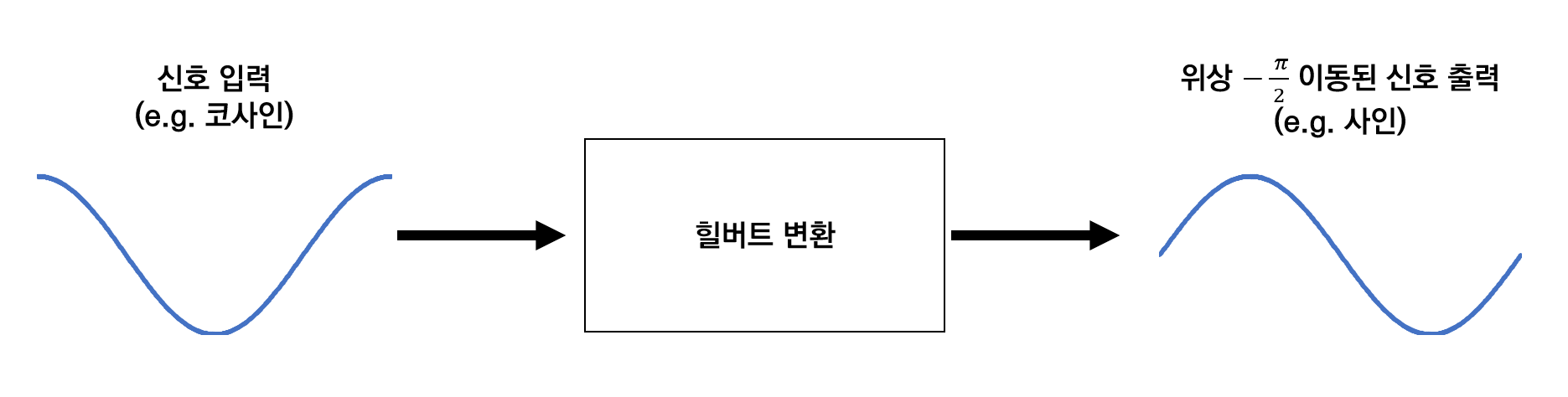
그림 1. 힐버트 변환은 원 신호의 amplitude는 유지하고 phase를 -90' shift 시킨다.

힐버트 변환의 특성

힐베르트 변환 필터의 특성은 모든 주파수에서 크기는 변하지 않고(all-pass filter) 위상만 음의 주파수에선 +90도, 양의 주파수에선 -90도로 변화시켜주는 필터이다. 즉 어떤 주파수의 $\cos \omega t$ 신호가 들어가면 항상 $\sin \omega t$ 신호가 나오는 것이다.

즉, 힐버트 변환을 정의함으로써 어떠한 실수 신호라도 그 신호를 $-\frac{\pi}{2}$ 또는 $\frac{\pi}{2}$ phase shift 시켜줄 수 있게 되는데, 그렇게 되면 실수 신호 를 복소수 차원으로 확장시킬 수 있게 되어서 amplitude와 phase의 분석이 쉬워지게 된다.

즉, 어떠한 실수 신호를 $x(t)$라 하고, 힐버트 변환 된 신호를 $\hat{x}(t)$라 했을 때, 복소수 차원으로 확장시켜 생각할 수 있는 신호 $x_p(t)=x(t)+j\hat{x}(t)$를 생각할 수 있게 되는 것이다.

가령 이 신호 $x(t)$가 $cos(\omega_0t+\theta)$인 경우에는 $x_p(t)=cos(\omega_0t+\theta)+j sin(\omega_0t+\theta)$라고 생각 할 수 있다. 이미 잘 알다시피 위의 $x_p(t)$는 $x_p(t)=e^{j(\omega_0t+\theta)}$로 표현할 수 있으며, 복소평면과 오일러 공식에 의해서 이 신호의 phase는 쉽게 구할 수 있게 된다. 이 처럼 실수차원의 신호를 복소수 차원으로 확장하여 해석하는 방법을 ‘해석적 표현(analytic signal)을 유도 한다’ 고 한다.

$x(t)$가 $cos(\omega_0t+\theta)$인 경우는 특별한 경우에 한하지만, 위와 같은 분석법은 어떠한 실수 신호에서라도 적용 가능하므로, 일반적인 실수 신호를 복소수 차원으로 확장해서 해석적 표현을 유도한다는 것은 매우 의미있는 과정이다.

힐버트 변환의 유도

힐버트 변환은 amplitude는 그대로 두고 phase만 변환시키는 역할을 한다. 따라서, 힐버트 변환은 일종의 all-pass 필터로 생각할 수 있으며, 위의 힐버트 변환의 특성을 만족시키는 transfer function은 다음과 같다.

\[|H(f)| = 1\]

이고

\[\angle H(f) = \begin{cases} \pi/2, & \text{for $f < 0$} \\ -\pi/2, & \text{for $f>0$} \end{cases}\]

그러므로 $H(f)=-j\times sgn (f)$라고 일반화 시킬 수 있다¹. 그러므로 변환 kernel인 impulse function $h(t)$는 $H(f)=-j\times sgn(f)$를 inverse Fourier Transform을 취함으로써 얻을 수 있다.

---

PROOF 힐버트 변환 kernel의 유도

\[h(t) = \int_{-\infty}^{\infty}{H(f) e^{j2\pi ft}df = \int_{-\infty}^{\infty}-j\times sgn(f)e^{j2\pi ft}df}\]

이 때, $sgn(f)$를 다음과 같이 근사시켜 생각할 수 있다.

\[sgn(f) \rightarrow G(f;\alpha) = \begin{cases} e^{-\alpha f}, & \text{for $f > 0$} \\ -e^{\alpha f}, & \text{for $f < 0$} \end{cases}\]

이 때, $G(f;\alpha)$는 $\alpha\rightarrow 0$로 근접할 때 $sgn(f)$와 매우 근사해진다는 것을 알 수 있다.

그러므로, 유도 과정에서는 $G(f;\alpha)$의 inverse Fourier transform을 생각하고, 이후 $\alpha\rightarrow 0$로 근접할 때의 $g(t)$의 모양을 생각하도록 하자.

그러므로,

\[h(t)=-j\lim_{\alpha\rightarrow 0}g(t;\alpha)\]

라고 할 수 있으며, $g(t;\alpha)$는 다음과 같이 유도할 수 있다.

\[g(t;\alpha) = \int_{-\infty}^{\infty}G(f;\alpha) e^{j2\pi ft}df\] \[= \int_{-\infty}^{0}-e^{\alpha f}e^{j2\pi ft}df + \int_{0}^{\infty}e^{-\alpha f}e^{j2\pi ft}df\] \[= \int_{-\infty}^{0}-e^{\alpha f+j2\pi ft}df + \int_{0}^{\infty}e^{-\alpha f+j2\pi ft}df\] \[= - \frac{1}{(\alpha + j 2\pi t)}\left|e^{(\alpha + j 2\pi t)f}\right|_{-\infty}^{0} +\frac{1}{(-\alpha + j 2\pi t)}\left|e^{(-\alpha + j 2\pi t)f}\right|_{0}^{\infty}\] \[= - \frac{1}{(\alpha + j 2\pi t)} (1-0) +\frac{1}{(-\alpha + j 2\pi t)} (0-1)\] \[= -\frac{1}{(\alpha + j 2\pi t)} - \frac{1}{(-\alpha + j 2\pi t)}\] \[=\frac{1}{(\alpha -j 2\pi t)} - \frac{1}{(\alpha + j 2\pi t)} = \frac{j4\pi t}{\alpha ^2 + (2\pi t)^2}\]

따라서,

\[h(t) = -j \lim_{\alpha \rightarrow 0}g(t;\alpha) = -j\lim_{\alpha \rightarrow 0}\frac{j4\pi t}{\alpha ^2 + (2\pi t)^2}\] \[= -j \frac{j4\pi t}{4\pi ^2 t^2} = -j \frac{j}{\pi t} = \frac{1}{\pi t}\]

---

일반적으로, 입력함수 $x(t)$에 대한 출력함수 $y(t)$는 시스템의 impulse response $h(t)$에 대해서

\[y(t)=x(t)\otimes h(t)=\int_{-\infty}^{\infty}{x(t)h(t-\tau)d\tau}\]

로 표현할 수 있으며, 힐버트 변환의 출력을 $y(t)$ 대신에 $\hat{x}(t)$라고 할 때, 다음이 성립한다.

\[\hat{x}(t) = \int_{-\infty}^{\infty}x(t) \frac{1}{\pi(t-\tau)d\tau}\] \[=\frac{1}{\pi}\int_{-\infty}^{\infty}x(t) \frac{1}{t-\tau}d\tau\]

힐버트 변환의 성질

신호 $x(t)$에 대한 힐버트 변환 결과를 $\hat{x}(t)$라고 할 때, 힐버트 변환은 다음과 같은 성질을 가진다.

힐버트 변환의 중복 적용

힐버트 변환을 두 번 취해주게 되면 원래 신호의 부호가 반전되는 결과를 가져온다. 이것은 phase shift를 $-\pi$ 또는 $\pi$만큼 시켜주기 때문. 이것을 수식을 이용해 표현하자면

\[\left(H(f)\right)^2 = \begin{cases} j \times j = -1, & \text{for $f < 0$} \\ (-j)\times (-j) = -1, & \text{for $f > 0$} \end{cases}\]

이다.

즉,

\[\hat{\hat{x}}(t) = -x(t)\]

삼각함수의 힐버트 변환

• $x(t) = \cos(2\pi f_0 t) \Leftrightarrow \hat{x}(t) = \sin(2\pi f_0 t)$

• $x(t) = \sin(2\pi f_0 t) \Leftrightarrow \hat{x}(t) = -\cos(2\pi f_0 t)$

• $x(t) = \exp(j2\pi f_0 t)$

\[\Leftrightarrow \hat{x}(t) = \begin{cases} -j \exp(j 2\pi f_0 t), & \text{for $f_0 > 0$} \\ +j \exp(j 2\pi f_0 t), & \text{for $f_0 < 0$} \end{cases} = -j\times sgn(2\pi f_0) \exp(j2\pi f_0 t) \notag\]

$x(t)$와 $\hat{x}(t)$는 같은 양의 에너지(또는 파워)를 가진다.

이것은 Parseval’s theorem으로부터 유도할 수 있다. $\hat{x}(t)$의 푸리에 변환을 $\hat{X}(f)$라고 했을 때, $\hat{X}(f)=-j\times sgn(f)X(f)$이므로,

\[\left|\hat{X}(f)\right| = \left|X(f)\right|\]

가 성립한다.

그러므로 아래와 같은 Parseval’s theorem에 의해 $x(t)$와 $\hat{x}(t)$의 에너지 또는 파워는 같은 값을 가진다는 것을 알 수 있다.

\[\int x^2(t) dt = \int \left|X(f)\right|^2 df\]

$x(t)$와 $\hat{x}(t)$는 직교함수이다.

다른 말로 $x(t)$와 $\hat{x}(t)$의 내적이 0이다. 즉,

\[\int_{-\infty}^{\infty}x(t)\hat{x}(t)dt = 0\]

이다.

이것 또한 Parseval’s theorem으로 증명할 수 있는데, 복소 신호에 대한 일반적인 Parseval’s theorem을 적용하면 위의 내적 값은 다음과 같아진다.

\[=\int_{-\infty}^{\infty}X(f)\hat{X}^*(f) df\] \[=\int_{-\infty}^{\infty}X(f)\space j \space sign(f) X^*(f)df\] \[=\int_{-\infty}^{\infty} j\space sgn(f) \left|X(f)\right|^2 df = 0\]

$\because sgn(f)$는 0에 대해 symmetric function이기 때문

Bedrosian identity (☆)

주파수 대역(spectra)가 겹치지 않는 두개의 신호 $c(t)$와 $m(t)$를 생각해보자. 이 때, $m(t)$가 lowpass filter이고 $c(t)$가 highpass filter라고 할 수 있으며 다음이 성립한다.

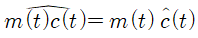
즉, $f_0$의 높은 주파수로 신호가 amplitude modulation된다고 했을 때, modulation되는 신호를 $m(t)$라고 하고 carrier signal을 $c(t)$라고 하면 다음이 성립한다.

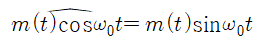
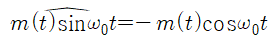
Signal의 Envelope

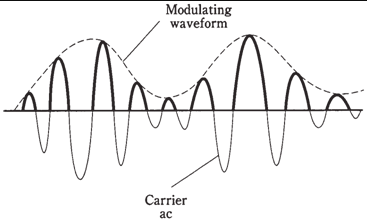
그림 2. Signal의 envelope이 말하는 것.
(출처 : http://www.expertsmind.com/CMSImages/2091_Detection%20of%20AM%20signals.png)

Bedrosian identity를 통해 amplitude modulation된 신호의 envelope를 구할 때 힐버트 변환을 활용할 수 있다.

즉, lowpass filter $m(t)$를 높은 주파수 $f_0$로 amplitude modulation 시킬 때, carrier signal을 $c(t)=cos(\omega_0 t)$라고 하면 AM signal은 $x(t)=m(t)c(t)$이다.

이 때, $x(t)$를 힐버트 변환하여 다음의 신호를 생각 할 수 있다.

\[x_p(t) = x(t) +j \hat{x}(t)\]

where

\[\hat{x}(t) = \sin (\omega_0 t)\]

이므로

\[x_p(t) = m(t) \cos(\omega_0 t) + j m(t) \sin (\omega_0 t) \notag\] \[=m(t) \exp(j\omega_0t)\]

이다.

그러므로,

\[\left|x_p(t)\right| = \left|m(t) \exp(j\omega_0 t)\right| = \left|m(t)\right|\]

이다. 따라서

\[|m(t)|\notag\]

는 AM signal의 envelope이다.