
선적분은 주어진 벡터장에 대해 지나간 경로를 따라 한 일을 구하는 문제와 같다.
그림 출처: Wikipedia, 벡터장의 선적분
물리학에서의 일(Work)
선적분의 개념을 적용하기에 가장 유용한 개념은 물리학에서의 “일”이다.
물리학에서 일은 다음과 같이 정의한다.
\[일 = 힘 \times \text{이동 거리}\]아래의 그림 1을 통해 철수가 한 일을 수식으로 표현하면 다음과 같이 생각할 수 있따.
철수가 $F$라는 힘으로 $s$ 만큼의 거리를 이동했을 때 철수가 한 일은 $W=Fs$이다.
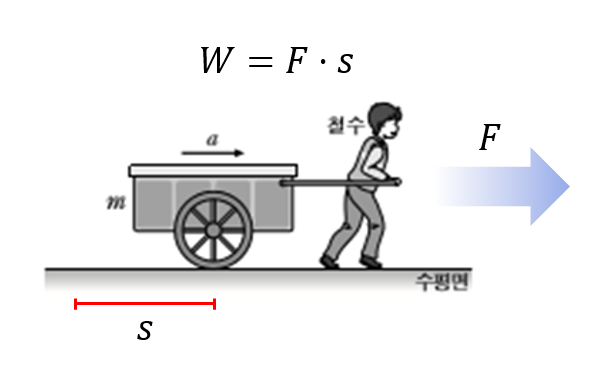
그림 1. 철수가 수레를 끌며 한 일은 힘과 이동거리를 곱한 만큼의 값이다.
그림 출처: EBS
그런데, 만약 철수가 수레를 밀 때 앞으로 똑바로 밀지 않고 어느정도의 각도를 가지고 윗쪽 사선 방향으로 밀어줬다고 생각해보자.
이럴 때는 수평면과 힘 벡터($\vec{F}$)와의 각도가 $\theta$라고 했을 때 아래와 같이 이동 거리와 관련된 방향 벡터와 내적하여 다음과 같이 계산할 수 있다.
\[W=\vec{F}\cdot \vec{s}=|\vec{F}||\vec{S}|\cos\theta\]
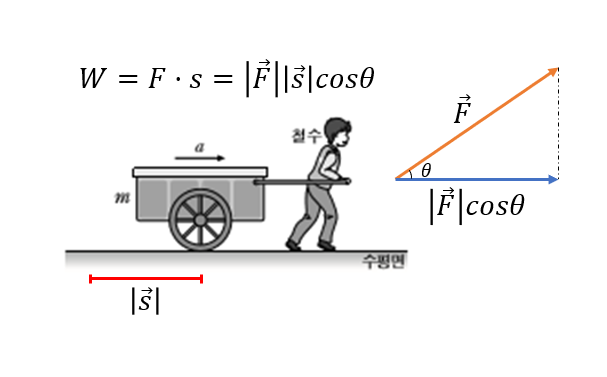
그림 2. 철수가 수레를 끌 때 수평면으로 똑바로 밀지 않고 비스듬하게 밀었을 때 철수가 수레를 끌며 한 일은 벡터의 내적으로 계산할 수 있다.
그림 출처: EBS
조금 더 복잡한 경로에 대해서…
이번엔 철수가 전체 거리를 이동하는 동안 세 번으로 나눠서 일을 다르게 했다고 생각해보자.
다시 말해, 아래의 그림 3과 같이 전체 이동 거리 중 세 개의 구간에서 사용한 힘의 크기가 서로 달랐거나, 힘을 준 각도가 서로 달랐을 경우를 상정해보자.
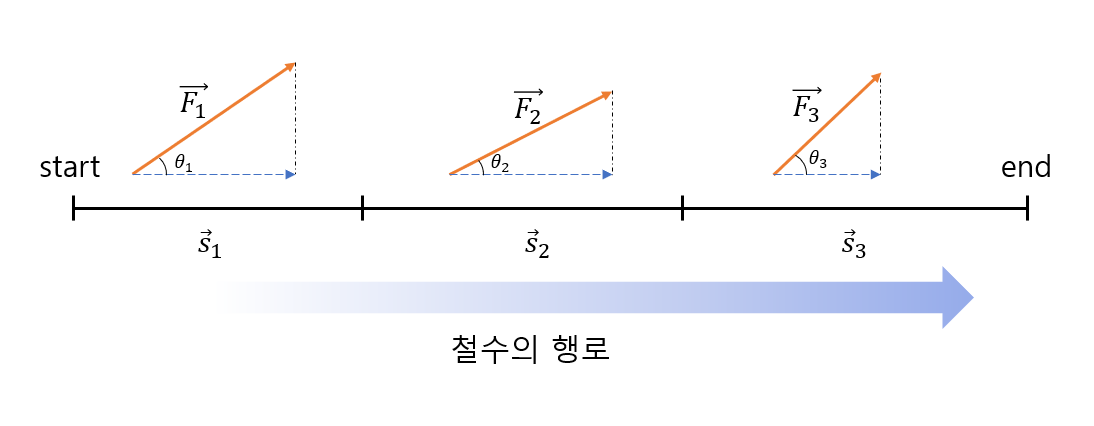
그림 3. 이동 경로를 세 구간으로 나누어 각 구간에서 한 일을 합치면 전체 구간에서 한 일을 구할 수 있다.
그러면 이 때 철수가 전체 이동 경로에서 해준 일은 다음과 같다.
\[W = W_1 + W_2 + W_3 = \sum_{i=1}^{3}\vec{F}_i\cdot \vec{s}_i\]그럼 이번엔 경로를 조금만 더 복잡하게 만들어 생각해보자.
그림 4와 같이 검은 실선으로 표현된 구불 구불한 경로에서 한 일을 계산하려면 빨간 점선으로 나타낸 것과 같이 직선적으로 여러 구간으로 경로를 나눈 뒤 각 경로에서 한 일을 모두 더해주면 된다.
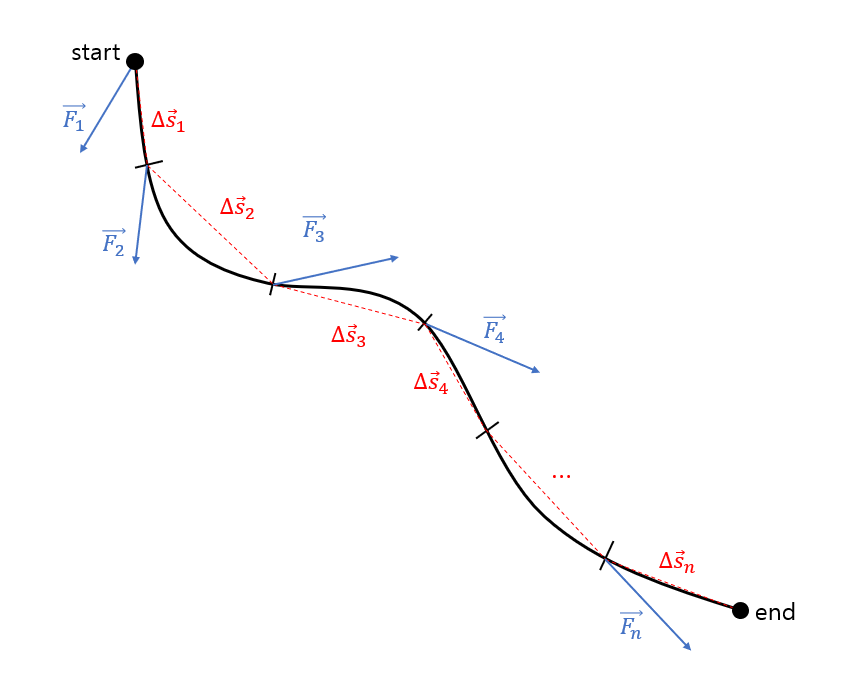
그림 4. 좀 더 구불구불하게 복잡한 경로에서 한 일을 계산하기 위해선 구간별로 잘게 잘라 각 구간에서 일한 일(Work)을 합하면 된다.
그림 4에서 표현하고 있는 일의 양을 수식으로 표현해주면 다음과 같다.
\[W = W_1+W_2+\cdots +W_n = \sum_{i=1}^{n}\vec{F}_i\cdot \Delta \vec{s}_i\]식 (4)와 같이 일을 계산할 때 경로를 무수하게 많이 쪼개려면 다음과 같이 생각할 수 있다.
\[W = \lim_{|\Delta \vec{s}|\rightarrow 0}\sum_{i=1}^{n}\vec{F}_i\cdot \Delta \vec{s}_i\]이 값을 우리는 line integral이라고 정의할 수 있다.
\[\Rightarrow \int_C\vec{F}\cdot d\vec{s}\]line integral
보통은 line integral을 표기할 때 식 (6)에서 사용한 적분인자($d\vec{s}$)를 $d\vec{r}$로 많이 쓴다.
\[\int_C\vec{F}\cdot d\vec{r}\]실제 문제에서는 그림 4에서 보는 $\vec{F}$들이 벡터장으로 주어지며 벡터장은 다음과 같이 보통 생각할 수 있다.
\[\vec{F(x,y)} = P(x,y)\hat{i} + Q(x,y)\hat{j}\]여기서 $F(x,y)$는 힘(Force)이 아니라 장(Field)를 의미하며, $P(x,y)$와 $Q(x,y)$는 모든 $(x,y)$ 좌표에서의 $x$ 성분과 $y$성분을 각각 의미한다.
또, 이동 경로로 표시한 curve는 $y=f(x)$처럼 주어질 수도 있고, $z=f(x,y)$ 혹은 아래와 같은 매개변수 방정식으로 주어질 수도 있다.
\[\begin{bmatrix} x(t) = g(t) \\ y(t) = h(t) \end{bmatrix}\]예시 문제 풀이
벡터장이 $F = xy\hat{i} -y^2\hat{j}$로 주어져 있을 때, 아래의 경로를 따라 한 일의 양을 구하시오.
\[y=\frac{1}{2}x\text{ where } 0<x<2\]
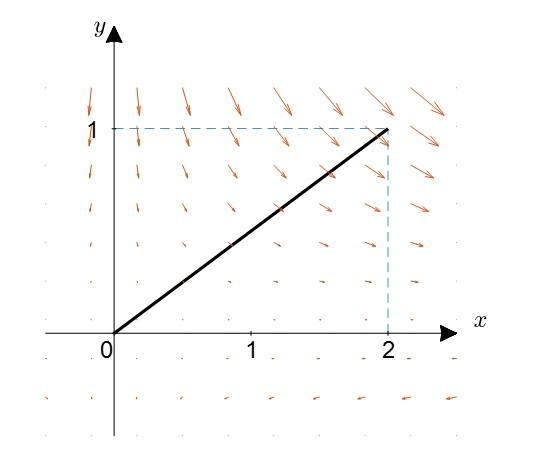
그림 5. 예시 문제의 벡터장과 이동 경로
우리가 구하려는 적분값은 다음과 같은데,
\[\int_C\vec{F}\cdot d\vec{r}\]여기서 $d\vec{r}$은 $x$방향으로의 성분 $dx$와 $y$방향으로의 성분 $dy$의 합으로 표현할 수 있으므로 다음과 같이 생각할 수 있다.
\[d\vec{r} = \hat{i}dx+\hat{j}dy\]따라서 주어진 벡터장 $\vec{F}$와 내적해 생각하면,
\[\vec{F}\cdot d\vec{r} = (xy\hat{i} - y^2\hat{j})\cdot (\hat{i}dx + \hat{j}dy) = xy(dx)-y^2(dy)\]여기서 경로는 $y=(1/2)x$로 주어져 있으므로 위 식에서 $y=(1/2)x$를 대입하면,
\[\vec{F}\cdot d\vec{r}\Rightarrow x\left(\frac{1}{2}x\right)dx-\left(\frac{1}{2}x\right)^2\left(\frac{1}{2}dx\right) =\left(\frac{1}{2}x^2-\frac{1}{8}x^2\right)dx\]따라서, 선적분 값은
\[\int_{0}^{2}\left(\frac{1}{2}x^2-\frac{1}{8}x^2\right)dx=\int_{0}^{2}\left(\frac{3}{8}x^2\right)dx=\left[\frac{1}{8}x^3\right]_{0}^{2} = 1\]임을 알 수 있다.