미분방정식의 해는 많은 경우 exponential 함수로 표현된다.
우리의 질문은 이렇게 귀결될 수 있다.
미분방정식은 ‘되먹임을 통한 성장’에 대한 기술(description)이기 때문이다.
Prerequisites
해당 내용에 대해 잘 이해하기 위해선 아래의 내용에 대해 잘 알고 오시는 것을 추천 드립니다.
미분방정식을 보는 또 다른 관점
우리는 지금까지 두 가지 관점으로 미분방정식을 생각해보았다.
미분방정식을 이용한 현상 모델링편에서는 미분계수가 포함된 방정식을 미분방정식이라고 보았다.
또, 방향장과 오일러 방법 편에서는 좌표 $(x,y)$에 매핑된 기울기로 미분방정식을 기하학적으로 해석했다.
이번 시간에는 또 다른 관점에서 미분방정식을 보고자 하는데, 그것은 되먹임(feedback)을 통한 연속 성장이다.
되먹임(feedback)이란 출력으로 나온 값을 가지고 다시 입력에 사용하는 것을 말한다.
그림 1. 입력과 되먹임(feedback)이 있는 시스템의 블록 다이어그램
미분방정식은 시간에 따른 성장
가령 아래와 같은 아주 간단한 미분방정식을 생각해보자.
\[\frac{dx}{dt}=f(t, x)\]위 식을 미분 계수의 정의를 이용해 미분 계수를 풀어서 적어보자.
\[\lim_{h\rightarrow 0}\frac{x(t+h)-x(t)}{h}=f(t, x)\]미분계수를 이해하는데 있어 가장 걸림돌이 되는 부분은 극한 개념의 도입이다.
우리는 극소값 $h$를 $\Delta t$와 같은 생각해보기 쉬운 작은 값으로 바꿔 놓고 수식을 더 풀어보자.
\[\Rightarrow \frac{x(t+\Delta t)-x(t)}{\Delta t} = f(t, x)\]그러면 아래와 같은 식이 보인다.
\[x(t+\Delta t) = x(t) + \Delta t f(t, x) % 식 (4)\]이 식이 말하는 것이 바로 현재 값 $x(t)$에서 $\Delta t f(t, x)$ 만큼 성장시켰을 때 다음번 스텝의 값 $x(t+\Delta t)$를 얻는다는 것이다.

그림 2. 미분방정식은 연속 성장을 통해 매 스텝마다 함수의 값이 어떻게 변해가는지를 기술한 것이다.
여기서 생각하는 타입 스텝 $\Delta t$는 실제 미분방정식을 생각할 때는 매우 작은 시간 단위에 대해 생각하는 것이므로, 우리는 이것을 연속성장과 관련된 값이라고 볼 수 있다.
되먹임을 통한 연속 성장
또 다시 식 (1)을 보자.
식 (1)을 보면, 식 (1)의 좌변은 매 시간 마다의 $x(t)$의 성장률에 대한 식이고 식 (1)의 우변에서는 그 성장률이 어떻게 계산되는지를 말해주고 있다.
미분방정식의 해는 초기값으로부터 주어진 성장량을 누적(즉, 적분)시켜가면서 얻은 결과물이다.
여기서 식 (1)에서 우변에 종속변수 $x$가 들어있다는 것이 매우 중요한데, 우변이 $x$에 관한 함수이여야만 비로소 ‘되먹임을 통한 연속 성장’이라고 할 수 있기 때문이다.
만약 우변에 독립변수 $t$에 관한 식만 들어있다면 이 미분방정식은 되먹임을 통한 연속 성장에 관한 기술(description)이라고 보긴 어렵다.
이것을 이해하기 위해 아래의 두 식의 차이를 생각해보자.
\[\frac{dx}{dt}=f(t) % 식 (5)\] \[\frac{dx}{dt}=f(x) % 식 (6)\]식 (5)와 식 (6)은 모두 성장에 관한 레시피이다. 왜냐면 좌변에는 성장률이, 우변에는 그 성장률을 기술할 다항식이 적혀있기 때문이다.
즉, 매 시점에 얼마만큼 성장해야 하는지가 기술(description)되어 있다.
그런데 식 (5)나 식 (6)을 식 (4)와 같은 방식으로 풀어쓰면 다음과 같을 것이다.
\[식(5)\Rightarrow x(t+\Delta t)=x(t)+\Delta t f(t)\] \[식(6)\Rightarrow x(t+\Delta t)=x(t)+\Delta t f(x)\]즉, 식 (5)는 현재 값에서 다음 값으로 넘어갈 때시간에 따른 성장률의 변화가 적용되는 레시피이고, 식 (6) 은 현재값에 관련된 성장 레시피가 적용되는 경우라고 할 수 있다.
다시 말해, 식 (1)의 우변에 $x$에 관한 함수가 있어야지만 되먹임을 통한 성장이라고 할 수 있다.
자연상수 e를 이용한 되먹임을 통한 연속 성장의 표현
그럼, 포스팅의 초반에 언급했던 내용인 미분방정식의 해가 $e^t$ 함수를 이용해 표현된다는 경우가 많다는 것과 되먹임을 통한 연속 성장은 어떤 관련이 있을까?
자연상수 e 편에서는 자연상수 $e$가 바로 연속 성장에 관한 성장량 그 자체라고 언급했다.
이 때, 우리는 연속 성장에 대해 알기 위해서 어떤 예시를 확인했었는가?
복리의 개념을 적용할 때 처럼 우리는 매 시간마다 지금까지 얻어진 결과물에 성장 비율을 곱해줘서 다음 번 성장 값을 얻어냈다.
즉, 지금까지 얻은 출력물을 가지고 다시 새로운 출력을 얻어내는 “되먹임을 통한 연속 성장”에 대해 생각해본 것이다.
구체적인 예시로써 다음과 같은 그림을 확인해보자.
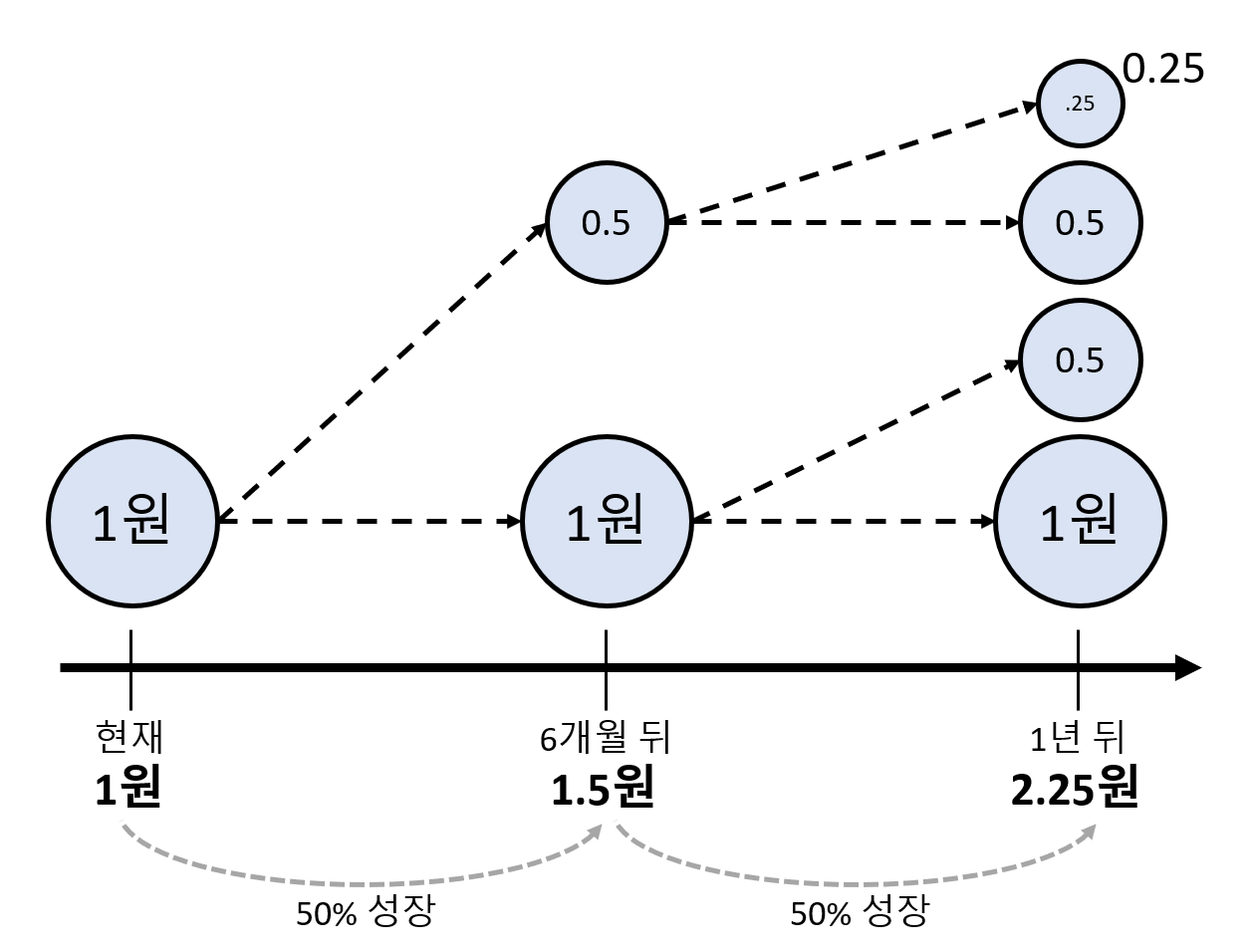
그림 2. 자연상수 e를 이해하는 과정에서 확인한 2회에 걸친 불연속 성장의 예시
위 그림에서는 2회에 걸쳐 불연속 성장을 했는데, 이 때, 1이라는 숫자를 1.5 곱해주고, 거기에 또 1.5를 한번 더 곱해주는 방식으로 결과값을 얻었다.
우리가 미분방정식을 푸는 과정도 마찬가지의 방법을 도입하는 것이다.
실제로 식 (1)의 우변에 $x$의 함수가 포함되어 있는 미분방정식을 풀면 그 해가 자연상수 $e$로 표현된다는 것을 알 수 있다.
간단한 예를 들어 아래와 같은 미분 방정식에 대해서,
\[\frac{dx}{dt}=x\]좌변을 모두 $x$에 관한 식으로, 우변을 모두 $t$에 관한 식으로 만들면,
\[\frac{1}{x}dx = dt\]와 같다는 것을 알 수 있고 양변에 적분 기호를 취해주면,
\[\int \frac{1}{x}dx=\int dt\]여기서 $1/x$의 부정적분이 자연로그이므로,
\[\Rightarrow \ln(x)=t+C\]라는 것을 알 수 있다. 여기서 $C$는 적분상수이다.
따라서,
\[x(t)=Ce^t\]이다.
제차 미분방정식의 의미
미분방정식을 공부하다보면 제차 미분방정식, 비제차 미분방정식이라는 용어와 만나게 된다.
제차 미분방정식이란 우리가 본 식 중 식 (6)에 해당한다. 식 (6)을 다시 써서 $x$에 관한 식을 모두 좌변에, $t$에 관한 식을 모두 우변에 넣으면 다음과 같은데,
\[\frac{dx}{dt}-f(x) = 0 % 식 (14)\]위 식을 잘 보면 우변에 $t$에 관한 항이 없다.
반면 비제차 미분방정식이란 우리가 본 식 중 식 (5)에 해당한다. 식 (5)는 다시 써보면,
\[\frac{dx}{dt}=f(t) % 식 (15)\]라고 쓸 수 있고 우변에 $t$에 관한 항이 남아 있다.
이것이 의미하는 것은 무엇일까?
식 (15)가 식 (14)와 다른점은 식 (15)는 $x(t)$가 시간에 따라 변해가는 법칙이 함수의 현재값에만 의존하는 것이 아니라 추가 파라미터 $t$에 의해서 함께 변해간다는 뜻이다.
다시 말해, 식 (14)에서 말하고 있는 식은 외부의 입력이 없는 자율적인 시스템을 구축한 셈이다.
식 (15)는 반대로 외부의 입력을 받아서 시시각각 시스템의 룰이 조금씩 변하고 있는 셈이다.
여기서 제차(齊次 혹은 동차 同次) 미분방정식의 의미는 ‘동일하다’ 혹은 ‘동등하다’라는 의미로 homogeneous를 번역한 것으로 보인다.
dictionary.com에서는 homogeneous의 수학적 의미로 ‘having a common property throughout’이라는 의미를 말해주고 있다.
즉, 시간이 지나더라도 변하지 않는 “일정한” 혹은 “동일한” 시스템을 유지하고 있는 시스템이다라는 뜻으로 이해해야 할 것으로 보인다.
다시 말해, 외부로부터 입력을 받지 않고 스스로의 시스템을 구축해 놓는 것이 제차 미분방정식이 갖고 있는 본질적 의미라고 생각하기 때문이다.