본 포스팅은 IIT의 S. C. Duta Roy 교수님의 강의를 정리한 것임을 먼저 밝힙니다.
목표
- Butterworth필터와 비교하여 Chebyshev 필터의 특징을 이해한다.
- Chebyshev Polynomial의 특징을 이해한다.
- Chebyshev 필터의 구현 조건인 $N$의 결정방법과 $\epsilon$의 결정 방법을 이해한다.
1. Chebyshev 필터의 특징
가. Introduction to Chebyshev Filter
Chebyshev 필터는 Butterworth 필터와 마찬가지로 일종의 All-Pole 필터로써 기본적으로 Lowpass Filter를 설계할 수 있도록 만들어진 필터이다.
앞선 Butterworth 필터 편에서도 설명했듯이, Chebyshev 필터의 경우에도 Chebyshev 필터를 통한 Lowpass filter 설계에 중심을 맞춰서 정리해 나갈 생각이다.
먼저, 개괄적으로, Chebyshev 필터는 elliptic filter를 제외하였을 때, 가장 ideal filter에 가까운 필터라고 할 수 있다. 그 이유는 같은 조건의 필터 차수($N$)와 specification requirement에 대해서 transition band가 가장 좁고, 가장 가파른 transition의 양상을 보이기 때문이다.
참고로 elliptic filter는 numerical method를 사용해야만 만들 수 있는 필터이기 때문에 elliptic filter를 제외하였을 때, Chebyshev 필터가 가장 ideal filter에 가까운 필터라고 하였다. 즉, coefficient를 수식을 통해서 구할 수 있는 필터 중에서는 Chebyshev 필터가 가장 optimal한 필터의 종류라고 할 수 있다.
나. Chebyshev 필터의 모양
그렇다면 Chebyshev 필터의 대략적인 모습을 보도록 하자.
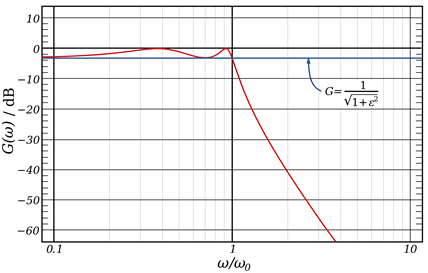
그림 1. Chebyshev 필터의 대략적인 형태
출처: 위키피디아 Chevyshev filter
외형에서 볼 수 있는 가장 큰 특징은 passband안에 있는 ripple이라고 할 수 있다.
조금 더 상세하게 Chebyshev 필터의 특징을 열거하면 다음과 같다.
① monotonic filter가 아니다.
② Equal ripple(Equi-Ripple)이 존재한다.
이 때, Type I의 Chebyshev 필터에서는 passband에 ripple이 있는데, stopband에서는 monotonic한 양상을 보인다.
이것은 Type II에서는 반대의 양상을 보이는데, type II는 type I을 뒤집으면 얻을 수 있는 것이다. 하지만 type I이 선호되는데, 그 이유는 type II는 lowpass filter의 역할 중, 불필요한 신호 제거에 취약하기 때문이다.
②의 이유에 대해서는 조금 뒤에 더 상세히 설명하겠지만, 그림에서와는 차이가 있는 것이, 실제로는 주기적인 모양을 가지는 ripple이 생기고, ripple에 대한 식 역시 존재한다. 그 ripple의 모양과 주기를 결정하는 식을 Chebyshev Polynomial이라고 하고, $C_N(x)$로 적는다.
다. 수식을 통해서 알 수 있는 것들은?
Chebyshev 필터는 다음과 같은 수식으로 정의된다.
\[|H_a(j\Omega)|^2 = A^2 / \left\lbrace 1+\epsilon^2 C_N\left(\frac{\Omega}{\Omega_p}\right)\right\rbrace\]또는
\[|H_a(j\Omega)| = A / \sqrt{ 1+\epsilon^2 C_N\left(\frac{\Omega}{\Omega_p}\right)}\]이 때, A는 gain factor이다. 보통, passband 주파수에서의 증폭을 원하는 경우가 아닌 경우 A=1로 둔다.
이 식을 잘 살펴보면, Chebyshev 필터의 특징을 볼 수 있는데, 이 때 특히 Butterworth 필터와 비교하여 살펴보면 좀 더 직관적인 이해를 도울 수 있다.Butterworth 필터의 식은 다음과 같았다.
\[|H_a(j\Omega)|^2 = 1/\left\lbrace 1+\left(\frac{\Omega}{\Omega_c}\right)\right\rbrace\]즉, Chebyshev 필터의 수식에는 Butterworth 필터의 수식에는 없는 것들이 있다. $\epsilon$과 $C_N(x)$가 그것이다. 그리고 Chebyshev 필터와 Butterworth 필터의 사소하지만 중요한 차이는 Chebyshev 필터의 수식에는 $\Omega_p$가 들어가있는 반면에, Butterworth 필터에서는 $\Omega_c$가 들어가있다는 점이다. 즉, Chebyshev 필터를 구현할 때에는 $\Omega_c$를 직접적으로 필요로 하지 않는다는 사실이다.
$\epsilon$은 ripple의 크기를 정하는 요소이고, $C_N(x)$는 필터의 차수 N에 의해서 정해지는 ripple의 모양이며, 이 $C_N(x)$는 다음과 같이 정의된다.
\[C_N(x) = \begin{cases}\cos(N\cos^{-1}(x)) && \text{ for } |x| \leq 1 \\\cosh(N\cosh^{-1}(x)) && \text{ for } |x| \gt 1\end{cases}\]이 식을 잘 살펴보면, 왜 $x$의 범위가 1을 중심으로 정의되는지 알 수 있다. 그것은 원래 $cos^{-1}(x)$의 함수가 $|x|\leq 1$에서 정의되기도 하고, $\Omega$가 $\Omega_p$보다 클 때와 작을 때의 $C_N(x)$의 값이 다르다는 것을 의미한다. 즉,
① $\cos(N\cos^{-1}(x))$는 어쨌든 cosine 함수이기 때문에 ripple이 생기며, 이 ripple은 $N\cos^{-1}(x)/{2\pi}$의 주기를 가진다.
② $\cosh(N\cosh^{-1}(x))$는 주기함수가 아니다. $\cosh(x)$함수는 Hyperbolic cosine이라고 읽고, 다음과 같이 정의된다.
\[\cosh(x) = \frac{e^x+e^{-x}}{2} = \cos(jx)\]그러므로, 수식을 통해서 보았을 때, $\Omega\leq\Omega_p$일 때는 주기성을 띄는 ripple을 가지는 함수이고, $\Omega>\Omega_p$의 범위에서는 monotonic 한 함수라는 것을 확인할 수 있다.
2. Chebyshev polynomial $(C_N(x))$
가. Chebyshev polynomial의 정의
다시 한번, Chebyshev Polynomial의 정의는 다음과 같다.
\[C_N(x) = \begin{cases}\cos(N\cos^{-1}(x)) && \text{ for } |x| \leq 1 \\\cosh(N\cosh^{-1}(x)) && \text{ for } |x| \gt 1\end{cases}\]우리는 이 때, $|x|\leq 1$인 경우에서의 $C_N(x)$에 관심이 있다는 것을 먼저 밝히고 싶다. 이것이 중요한 이유는, $C_N(x)$의 성질에 의해서 Chebyshev 필터의 모양이 결정되기 때문이다.
나. Analyzing Chebyshev polynomial
먼저, 우리는 $C_N(x)=\cos(N\cos^{-1}(x))$에 대해서 해석하는 것을 다시 한번 밝힌다. 이 때, $N$이 변함에 따라서 $C_N(x)$의 모양을 분석해보고자 한다. 이것은 Chebyshev 필터의 주요한 결정 요소는 필터의 차수 $N$과 ripple의 크기요소인 $\epsilon$이기 때문이다.
\[C_0(x) = 1\] \[C_1(x) = \cos(1\times \cos^{-1}(x)) = x\]$C_2(x)$을 구하려면, 약간 머리를 써야한다.
\[C_2(x) = \cos(2\cos^{-1}(x))\]여기서 $cos^{-1}(x)=\theta$라고 하자. 그러면 $x=cos(\theta)$이다. 그러므로,
\[C_2(x) = \cos(2\theta) = 2\cos^2\theta - 1 = 2x^2 - 1\]$C_3(x)$도 비슷한 방법으로 구할 수 있다.
\[C_3(x) = \cos(3\cos^{-1}(x))\]마찬가지로, $\cos^{-1}(x)=\theta$라고 하자. 그러면 $x=\cos(\theta)$이다. 그러므로,
\[C_3(x) = \cos(3\theta) = \cos(2\theta + \theta)\]여기서
\[\cos(2\theta + \theta)=\cos(2\theta)\cos(\theta) - \sin(2\theta)\sin(\theta)\] \[=(2\cos^2(\theta)-1)\cos(\theta) - 2\sin(\theta)\cos(\theta)\sin(\theta)\] \[=(2\cos^3(\theta) - \cos(\theta))-2(1-\cos^2(\theta))\cos(\theta)\] \[=2\cos^3(\theta) - \cos(\theta) - 2\cos(\theta) + 2\cos^2(\theta)\] \[=4\cos^3(\theta)-3\cos(\theta)\]따라서 원래의 $C_3(x)$는
\[\Rightarrow C_3(x) = 4x^3-3x\]이 때, $C_N(x)$의 모양을 보면, $x$의 차수가 2차가 차이가 난다는 것을 알 수 있다.
그러므로, 일반적으로
\[\cos(x) + \cos(y) = 2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right)\]임을 이용하면,
\[\cos(N\theta) + \cos((N-2)\theta) = 2\cos(\theta)\cos((N-1)\theta)\]이므로,
\[\cos^{-1}(x) = \theta, x = \cos(\theta)\]라는 식을 이용해서,
\[C_N(x) = \cos(N\cos^{-1}(x))\]이고,
\[C_N(x) = \cos(N\theta)\]이기 때문에,
\[C_N(x) = 2xC_{N-1}(x) - C_{N-2}(x)\]라는 사실을 유도해 낼 수 있다.
그러므로, 일반적인 $C_N(x)$의 식을 유도해 낼 수 있다.
그래서, 예를 들면,
\[C_3(x) = 2x(2x^2 -1) -x\] \[= 4x^3 - 3x\] \[C_4(x) = 2xC_3(x) - C_2(x)\] \[=2x(4x^3-3x) - (2x^2 - 1)\] \[=8x^4 - 8x^2 + 1\]같은 방식으로 어떤 $C_N(x)$이든지 N의 크기에 상관없이 회귀적으로 그 값을 구해낼 수 있게 되었다.
몇 개의 $C_N(x)$를 모아보았다.
\[C_0(x) = 1\] \[C_1(x) = x\] \[C_2(x) = 2x^2 - 1\] \[C_3(x) = 4x^3 - 3x\] \[C_4(x) = 8x^4-8x^2 + 1\]이렇게 $C_N(x)$를 모아놓고 보면, $C_N(0)$은 특이한 주기성을 가진다는 것을 알 수 있다.
그것은,
\[C_N(0) = \begin{cases}0 && N = \text{odd}\\\pm 1 && N = \text{even}\end{cases}\]이라는 것이다. 이것은 나중에 $\Omega=0$의 Chebyshev 필터의 모양을 결정하는데 중요한 역할을 한다.
또한 $C_N(x)$의 Polynomial을 모아서 보면 다음과 같다.
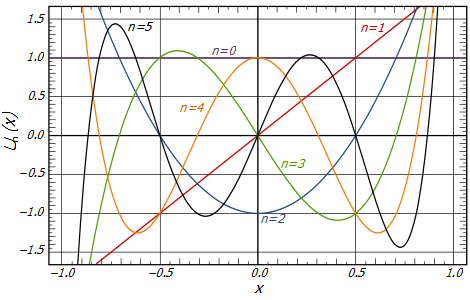
그림 2. 여러가지 n에 대한 Chebyshev Polynomial
출처: 위키피디아 Chevyshev filter
이 때, $|x|>1$인 $x$에 대해서는 해당 색깔의 선을 따라 연속적으로 그어주면 된다. 그것은 $C_N(x)$는 $|x|>1$에 대해서는 $C_N(x)=\cosh(\cosh^{-1}(x))$로 정의되기 때문이고, 이것은 다시 말하지만 monotonic한 모양을 가진다.
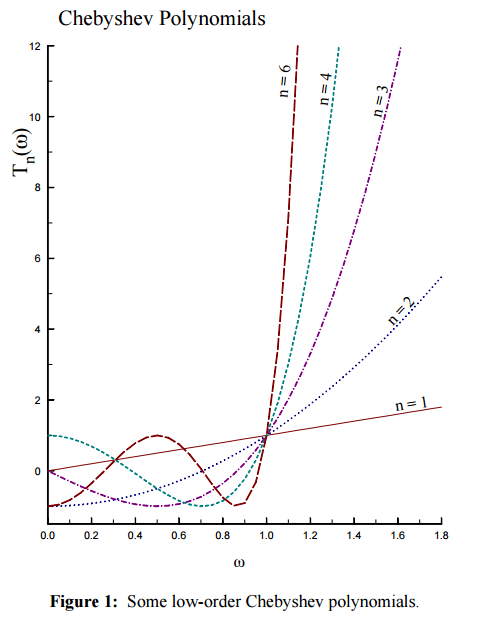
그림 3. 여러가지 n에 대한 Chebyshev Polynomial을 $\|x\|>1$인 경우에 대해서 까지 연장해 그린 것
(출처 : EE648 Chebyshev filters / John Stensby / ece.uah.edu)
그러므로, Chebyshev 필터에서 보이는 ripple은 equally oscillating 한다는 것을 알 수 있다.
다. N의 크기에 따른 Chebyshev filter의 모양
다시 한번 Chebyshev 필터의 수식을 써보자면 다음과 같았다.
\[|H_a(j\Omega)| = A / \sqrt{ 1+\epsilon^2 C_N\left(\frac{\Omega}{\Omega_p}\right)}\]여기서 우리는 Chebyshev filter의 모양을 그리기 위해서 $|H_a(j\Omega)|$의 최대값과 최소값을 생각해보자.
$0\leq\Omega\leq\Omega_p$에서 $C_N$이 oscillating 하고, 그 값은 $0\leq C^2_N\leq 1$이다.
\[\frac{A}{\sqrt{1+\epsilon^2}}\leq|H_a(j\Omega)|\leq A\]만약 여기서 $A=1$이라고 한다면,
\[\frac{1}{\sqrt{1+\epsilon^2}}\leq|H_a(j\Omega)|\leq 1\]그러므로, 각 필터의 차수 N에 대하여 그 모양을 보게 되면,
$N=1$일 때,
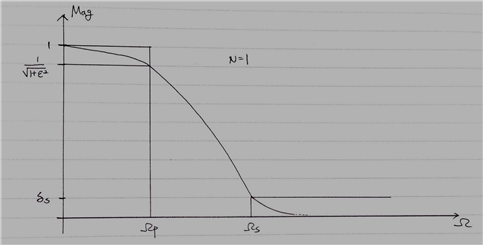
그림 4. $N=1$인 경우의 Chebyshev 필터의 형태
$N$이 홀수이기 때문에 $C_1(0)=0$이다. 또한, $|H_a(j\Omega)|_{\Omega = 0}=1$이다.
그렇기 때문에 N=1일 때, Chebyshev 필터는 1부터 시작한다는 것을 알 수 있다. 또한 N=1일 때는 Butterworth 와 같은 모습을 갖는다는 것도 알 수 있다. 하지만 $\epsilon$ 값을 어떻게 주는가에 따라서 Butterworth와 같은 값을 가질 수도 있고 아닐 수도 있기 때문에 모양이 같다고 해서 같은 필터가 되는 것은 아니다.
$N=2$일 때,
\[C_2(0)=2\times0^2-1=-1\]이고,
\[C_2(\Omega_p)=1\]이다. 따라서,
\[|H_a(0)|=\frac{1}{\sqrt{1+\epsilon^2}}\]이라는 점에 주의해 필터의 형태를 그려보면 다음과 같다.
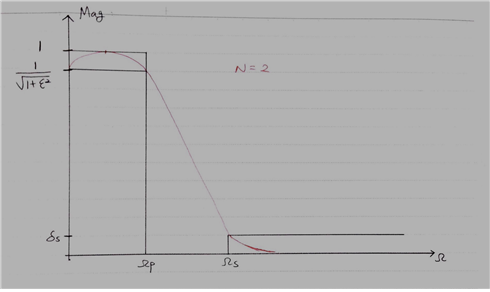
그림 5. $N=2$인 경우의 Chebyshev 필터의 형태
N=3, N=4에 대해서도 각각의 Chebyshev filter를 그려볼 수 있다.
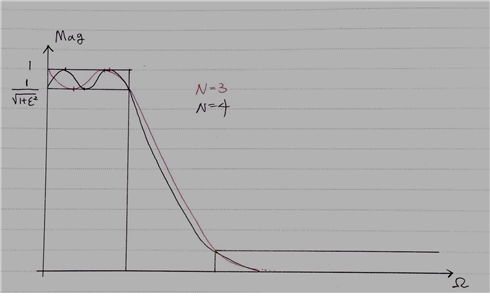
그림 6. $N=3$, $N=4$인 경우의 Chebyshev 필터의 형태
여기까지 보았을 때, 모든 Chebyshev 필터는 공통점을 갖고 있는데, 그것은 모든 Chebyshev 필터는 $N$의 크기에 상관없이
\[\left(\Omega_p, \frac{1}{\sqrt{1+\epsilon^2}}\right)\]점을 통과한다는 사실이다.
그것은 모든 Chebyshev Polynomial은 $(1,1)$을 통과하기 때문이라고 할 수도 있고,
$C_N(x)=\cos(N\cos^{-1}(x))$에서 $C_N(x)=\cos(N\cos^{-1}(x))=\cos(N\times 2\pi)=1$이기 때문이라고 직접 증명 할 수도 있는 것이다. 후에 이 사실을 이용해서 $N$의 크기를 계산할 수 있게 될 것이다.
몇 가지 사실에 대해 간단하게 정리하자면,
① The number of Maxima & Minima within the Passband = N
② If $N$ = even, starting point = $1/\sqrt{1+\epsilon^2}$
else if $N$ = odd, starting point = $1$
여기서 한 가지 더 생각해보아야 할 것은 3dB frequency (or cutoff frequency)를 찾는 방법이다. 이것은 간단하게, 3dB의 정의를 이용하면,
\[|H_a(j\Omega)|^2 = \frac{1}{2}\]이므로,
\[1/\left\lbrace1+\epsilon^2C_N\left(\frac{\Omega_{3dB}}{\Omega_p}\right)\right\rbrace=\frac{1}{2}\] \[\therefore \epsilon^2 C^2_N\left(\frac{\Omega_{3dB}}{\Omega_p}\right)= 1\] \[C_N\left(\frac{\Omega_{3dB}}{\Omega_p}\right)=\frac{1}{\epsilon}\]일반적으로, $\epsilon$은 “작은 값”으로 정의하는데, Chebyshev 필터의 특성 상, $\epsilon$은 1보다 작은 값이 되어야 한다. 그러므로, $C_N(x)=\cosh(N\cosh^{-1}(x))$를 사용하면,
\[\cosh\left(N\cosh^{-1}\left(\frac{\Omega_{3dB}}{\Omega_p}\right)\right)=\frac{1}{\epsilon}\] \[\therefore \Omega_{3dB}=\Omega_p\left\lbrace\cosh\left(\frac{1}{N}\cosh^{-1}(1/\epsilon)\right)\right\rbrace\]3. General transfer function of Chebyshev filter in s-domain
가. Finding poles of chebysehv filter
pole의 정의에 따라, pole은 다음 식을 만족하는 s와 같다고 할 수 있습니다.
\[1+\epsilon^2C^2_N\left(\frac{s}{j\Omega_p}\right) = 0\]하지만, 안타깝게도, 이 식을 푸는데 필요한 algebra가 저에겐 너무 복잡해서 다 이해하지 못했습니다. 그렇기 때문에 pole을 구하는 algebra에 대해서는 그 설명을 생략합니다.
하지만, 결론적으로는 이 pole을 구하게 되면 Butterworth filter의 pole과는 다르게 타원 위에 위치하게 된다고 합니다. 자세한 풀이과정은 위키피디아를 참고하길 바랍니다.
나. The transfer function of Chebyshev filter
Chebyshev Filter의 경우도 Butterworth Filter와 마찬가지로 N의 크기가 짝수 일 때와, 홀수 일 때의 경우의 두 가지 경우로 나뉜다. 이것은 위에서 N의 차수에 따른 Chebyshev 필터의 전반적 모양에서 본 것에서도 알 수 있듯이, N의 홀수 짝수 여부에 따라 그 시작점이 다르기 때문에 N의 홀수 짝수 여부에 따라 그 식도 달라진다고도 볼 수 있다.
$N$ : odd
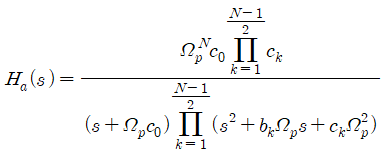
$N$ : even
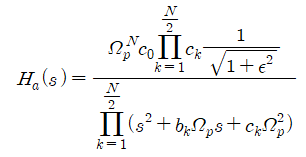
위 식을 통해서 다시 한번 알 수 있듯이, N이 짝수일 때에는 시작점이 $1/\sqrt{1+\epsilon^2}$이기 때문에 그 값이 분자에 곱해져 있다는 것을 알 수 있다. 각 상수 $c_0,b_k,c_k$에 대해서 설명하자면,
\[c_0 = y_N\] \[c_k = y^2_N+\cos^2\left(\frac{2k-1}{2N}\pi\right)\] \[b_k = 2y_N\sin\left(\frac{2k-1}{2N} \pi\right)\] \[y_N = \frac{1}{2}\left\lbrace \left(\sqrt{1+\frac{1}{\epsilon^2}}+\frac{1}{\epsilon}\right)^{\frac{1}{N}} - \left(\sqrt{1+\frac{1}{\epsilon^2}}+\frac{1}{\epsilon}\right)^{-\frac{1}{N}}\right\rbrace\]와 같다고 할 수 있다. 이제 마지막으로 N과 $\epsilon$을 정하는 방법에 대해서 생각해보아야 할 것이다.
다. $N$과 $\epsilon$을 결정하는 방법
일반적으로 필터를 구할 때에 받는 specification은 $\Omega_p, \Omega_s, \delta_p, \delta_s$라는 사실에 대해서 인지하고 있어야 한다. 이 값은 필터가 가졌으면 하는 요구조건이기 때문이다. 이것은 수학적으로 정해주는 것이 아니라, 필터의 설계자가 정하는 것이거나 요구하는 사장님이 정해주는 것이다.
일반적으로, specification의 관계를 표현하자면 다음과 같이 그릴 수 있다.
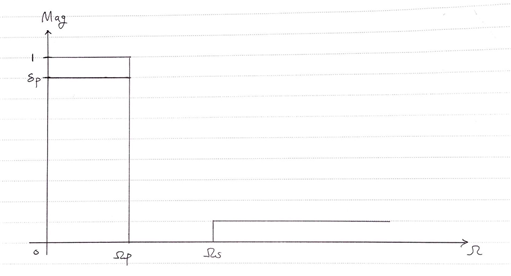
그림 7. 필터 설계 시 주어지는 specifictaion
위에서 설명했던 것과 같이 $\delta_p$는 주어진 값이기 때문에,
\[\delta_p = \frac{1}{\sqrt{1+\epsilon^2}}\] \[\therefore \epsilon = \sqrt{\frac{1}{\delta^2_p-1}}\]와 같이 $\epsilon$을 정할 수 있다.
$N$은 다음과 같이 정할 수 있다.
$\delta_s$도 주어진 값이라는 사실을 이용하면,
\[1/\left\lbrace1+\epsilon^2 C_N\left(\frac{\Omega_s}{\Omega_p}\right)\right\rbrace=\delta_s^2\] \[\therefore\epsilon^2 C^2_N\left(\frac{\Omega_s}{\Omega_p}\right)=\frac{1}{\delta_s}-1\] \[C_N\left(\frac{\Omega_s}{\Omega_p}\right)=\sqrt{\frac{1/\delta_s^2-1}{1/\delta^2_p - 1}}\]이 때,
\[\left(\frac{\Omega_s}{\Omega_p}\right)\gt 1\]이므로,
\[C_N\left(\frac{\Omega_s}{\Omega_p}\right)=\cosh\left(N\cosh^{-1}\left(\frac{\Omega_s}{\Omega_p}\right)\right) = \sqrt{\frac{1/\delta_s^2-1}{1/\delta^2_p - 1}}\] \[N_C\geq\frac{\cosh^{-1}\left(\sqrt{\frac{1/\delta_s^2-1}{1/\delta^2_p - 1}}\right)}{\cosh^{-1}\left(\frac{\Omega_s}{\Omega_p}\right)}\]을 만족하는 $N_C$를 찾을 수 있다. (여기서 $N_C$의 $C$는 Chebyshev를 의미하고자 했다.)
참고로, Butterworth filter의 차수 $N_B$는 다음과 같았다.
\[N_B\geq \frac{\log_{10}\sqrt{\frac{1/\delta^2_s-1}{1/\delta^2_p-1}}}{\log_{10}\left(\frac{\Omega_s}{\Omega_p}\right)}\]결국 Chebyshev 필터와 Butterworth 필터에서의 N을 구하는 방법은 매우 닮아있다고 할 수 있다.