s-plane에서 z-plane으로의 변화
슬라이더를 움직여 보세요 ^^

라플라스 변환과 z-변환

※ 이 꼭지는 Z 변환 포스트의 Z-변환과 라플라스 변환 꼭지에서 가져왔습니다.

Z-변환은 라플라스 변환의 discrete time 버전이라고 할 수 있다.

라플라스 변환의 식에서 시간 sampling을 해줌으로써 Z-변환을 얻어보자.

연속시간 신호$x(t)$에 대해 라플라스 변환은 다음과 같이 정의된다.

\[\mathfrak{L}\left[x(t)\right] = X(s) = \int_{0^{-}}^{\infty}x(t) e^{-st}dt\]

여기서 연속시간 신호 $x(t)$를 시간 샘플링하기 위해, 샘플링 주기 $T$에 대해 $t\rightarrow nT$로 치환하도록 하자.

즉,

\[X(s) = \int_{0^{-}}^{\infty}x(t) e^{-st}dt \big |_{t\rightarrow nT}\]

와 같은 과정을 거치며 여기서 $x(nT)$는 discrete time signal로 볼 수 있다. 따라서,

\[X(z) = \sum_{n=0}^{\infty}x(nT)e^{-snT}\]

여기서 $z = e^{sT}$를 대입하면,

\[식(3) \Rightarrow \sum_{n=0}^{\infty}x[n]z^{-n}\]

위 유도과정을 통해서 Laplace와 Z-transform이 수식적으로 연관되어 있다는 사실을 확인할 수 있다. 결론적으로 Laplace 변환과 Z 변환은 각각의 복소수를 정의해주는 방법에 차이가 있을 뿐 모두 system의 특성을 확인하기 위한 테크닉이라고 할 수 있겠다.

s-plane과 z-plane은 다음과 같은 형태학적 관계를 가지게 된다.

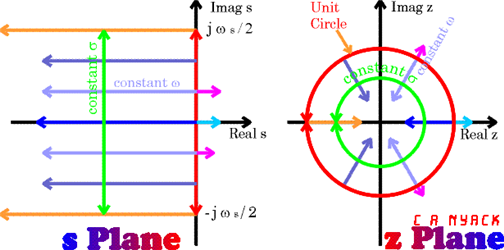
그림 1. s-plane과 z-plane의 관계. z-plane은 s-plane을 말아 넣은 것 같은 형태를 띄고 있다.

그림 1에서 처럼 s-plane에서는 세로축 기준 왼쪽에 pole이 위치해야 stable system이고 z-plane에서는 단위원 기준 안쪽에 pole이 위치하면 stable system이다.