슬라이더를 움직여 보세요 ^^
오일러 공식이란
우선 오일러 공식을 직접 써보도록 하자.
\[e^{i\theta} = \cos(\theta) + i\sin(\theta)\]식 (1)에서 볼 수 있듯이 오일러 공식은 여러가지 요소들이 혼합되어 있는데, 그 중 가장 독특한 것은 허수 승수라고 할 수 있을 것 같다.
이번 article에서는 이 복잡해 보이기만 하는 수식의 의미에 대해서 알아보도록 하자.
기하학적 의미
오일러 공식을 들여다보면 자연상수 $e$, 허수 $i$, 삼각함수 $\cos, \sin$가 들어있음을 알 수 있다.
처음 보기에는 허수 승수가 있는 좌변으로부터 어떤 정보를 알기는 어렵기에 공식의 우변으로부터 의미를 파악해보자.
공식의 우변으로부터
식 (1)의 우변을 다시 쓰면 다음과 같다.
\[\cos(\theta) + i \sin(\theta)\]$\cos(\theta)$와 $\sin(\theta)$를 각각 $x, y$로 놓고 생각해보면 식 (2)는 다름아닌 $x+iy$ 에 지나지 않는 것을 알 수 있다.
즉 식 (1)의 우변에서 좌변으로 오일러 공식의 의미를 생각해본다면 $e^{i\theta}$는 어떤 복소수라는 의미이다.
그리고 그 복소수가 길이가 1인 막대가 실수축으로부터 $\theta$ 라디안만큼 회전한 곳에 위치하는 값이라는 의미를 갖는다는 것이다.
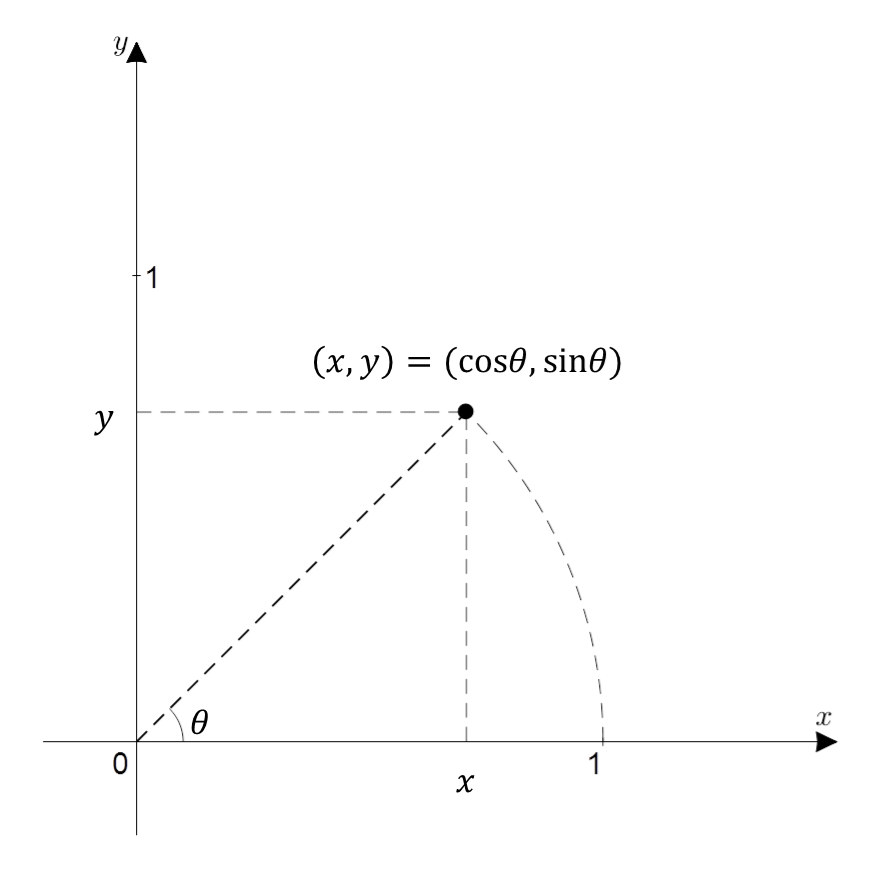
그림 1. 복소 평면 상에서 표현한 x+iy. 삼각함수로 표현하면 x축으로부터의 각도를 theta 라디안이라 했을 때 cos(theta) + i sin(theta)이다.
공식의 좌변으로부터
이번엔 식 (1)의 좌변을 생각해볼 차례인데, 결국 우리가 $e^{i\theta}$라는 것이 복소수이며,
이 복소수는 길이가 1인 막대가 실수축으로부터 $\theta$ 라디안만큼 회전한 곳에 위치하는 값이라는 의미를 찾을 것이라는 걸 염두에 두도록 하자.
일단 자연상수 $e$의 정의부터 생각해보면 자연상수 $e$는 다음과 같이 정의되었다.
\[e = \lim_{n\rightarrow \infty}\left(1+\frac{1}{n}\right)^n\]그러면 자연상수 $e$에 지수 $x$ 승이 붙은 경우는 어떻게 생각했더라…?
\[e^x = \lim_{n\rightarrow \infty}\left(1+\frac{x}{n}\right)^n = \left[\lim_{n\rightarrow \infty} \left(1+\frac{x}{n}\right)^{n/x}\right]^x\]그렇다면 식 (4)를 잘 생각해보면 자연상수 $e$에 허수지수 $i$가 붙은 것은 다음과 같이 생각해볼 수 있다.
\[e^i = \lim_{n\rightarrow \infty}\left(1+\frac{i}{n}\right)^n = \left[\lim_{n\rightarrow \infty} \left(1+\frac{i}{n}\right)^{n/i}\right]^i\]식 (5)의 중간에 있는 식만을 따로 떼서 보면 아래의 식과 같다.
\[\lim_{n\rightarrow \infty}\left(1+\frac{i}{n}\right)^n\]우리는 이 식 (6)의 의미에 대해 차근 차근 생각해보도록 하자.
자연상수에 붙은 허수 지수: 호(arc) 위의 점
식 (6)에서는 $n$을 무한대로 크게 만들어버렸지만, 일단은 $n$이 1인 경우부터 생각해보자.
n = 1 인 경우.
\[\text{n=1 }\Rightarrow \left(1+\frac{i}{1}\right)^1\]즉, 이것은 $1+i$라는 복소수를 의미한다. 그림으로 표현하면 아래와 같다.
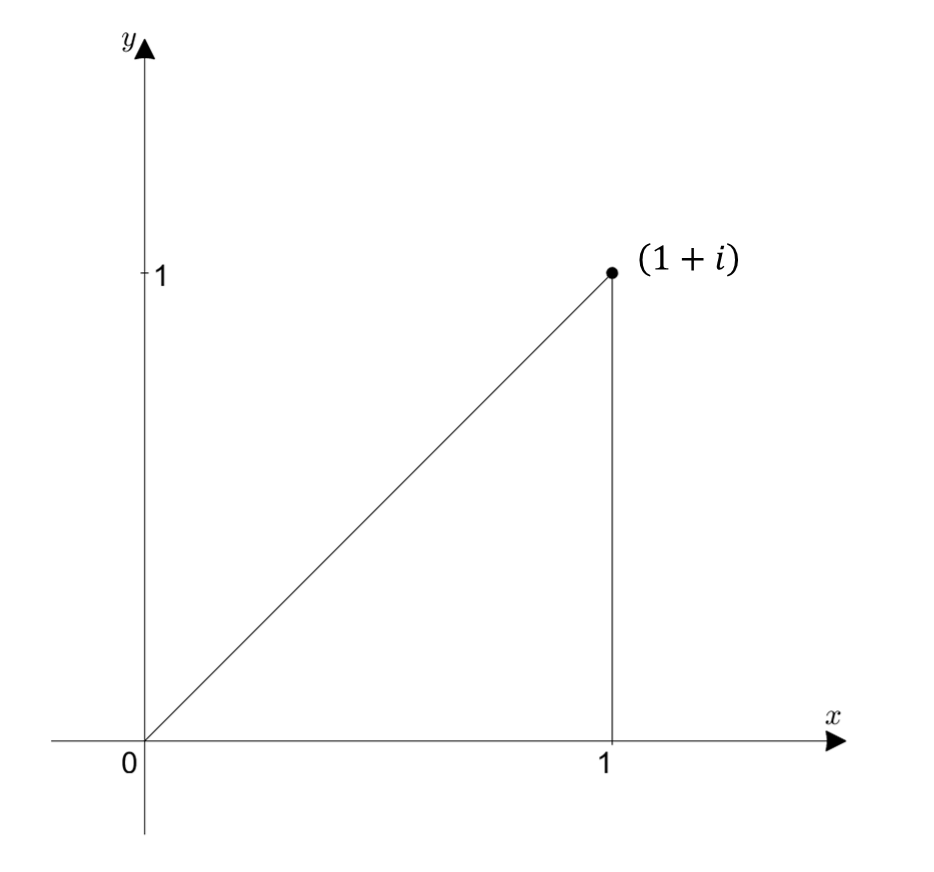
그림 2. 1+i의 복소 평면 상에서의 위치.
이번엔 n = 2 인 경우를 생각해보자.
\[\text{n=2 }\Rightarrow \left(1+\frac{i}{2}\right)^2 = \left(1+\frac{i}{2}\right)\left(1+\frac{i}{2}\right) = 0.75+i\]여기서 $\left(1+\frac{i}{2}\right)\left(1+\frac{i}{2}\right)$을 어떻게 쉽게 이해할 수 있을까?
한마디로 설명하면 $(1+i/2)$를 그려서 얻은 직각 삼각형에 대해 그 빗변의 길이에 1/2의 길이만큼을 높이로 하는 직각 삼각형을 한번 더 그림으로써
$\left(1+\frac{i}{2}\right)\left(1+\frac{i}{2}\right)$을 기하학적으로 그릴 수 있게 된다.
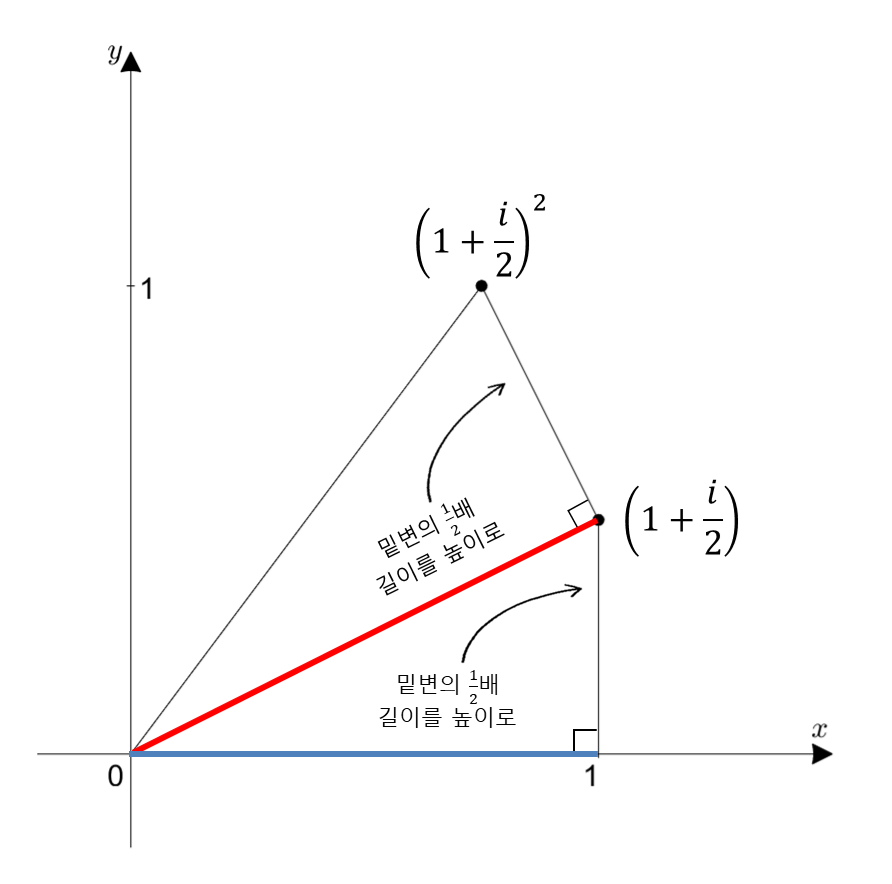
그림 3. (1+i/2)^2의 복소 평면 상에서의 위치를 생각하는 방법
마찬가지 방법으로 n = 3 인 경우는 다음과 같이 이해할 수 있다.
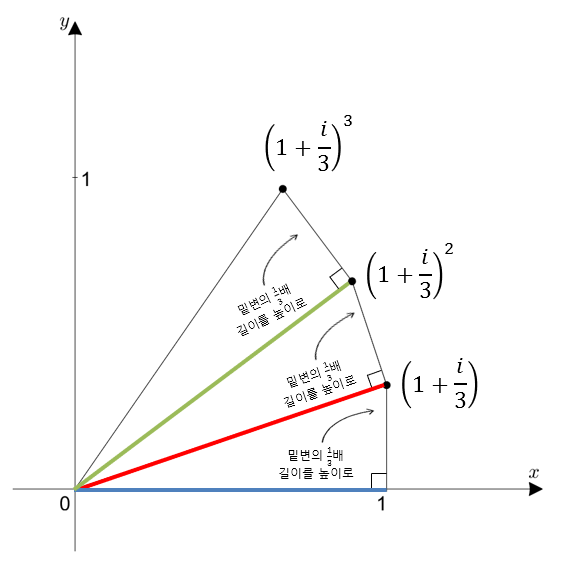
그림 4. (1+i/3)^3의 복소 평면 상에서의 위치를 생각하는 방법
같은 방식으로 n = 10인 경우를 생각해보면 다음과 같다.
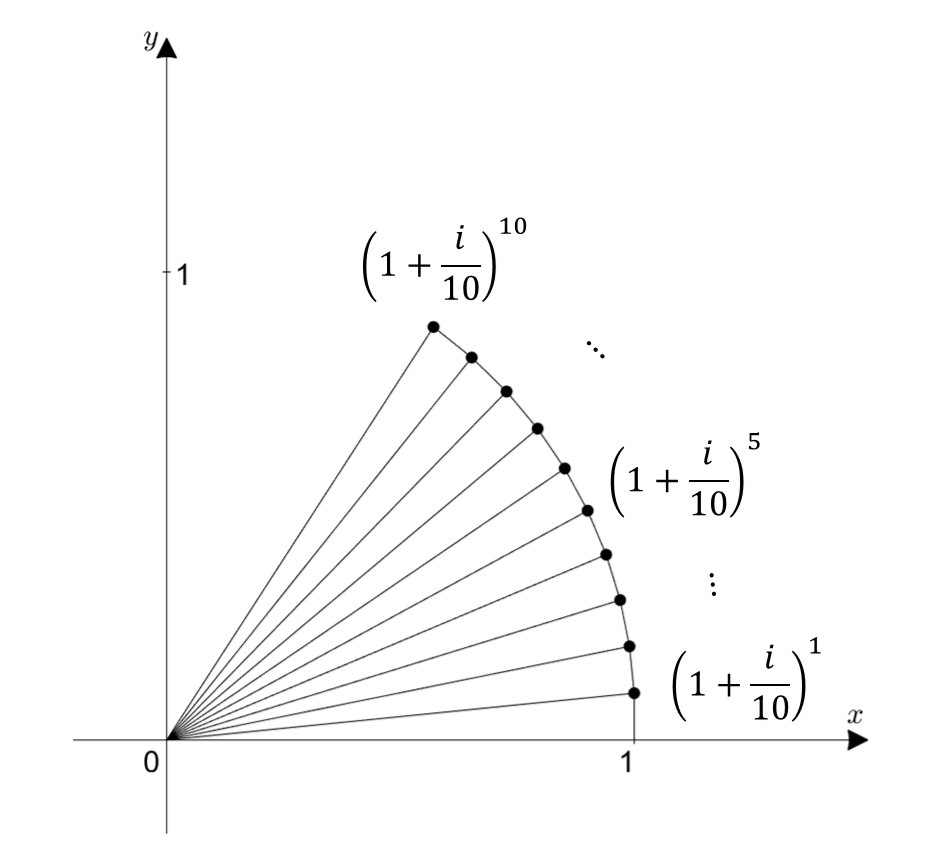
그림 5. (1+i/10)^10의 복소 평면 상에서의 위치를 생각하는 방법
$n$이 커지면 커질 수록 1과 $1/n$을 밑변고 높이로 하는 직각 삼각형의 빗변의 길이는 거의 1에 가까워지며,
$n$이 커질 수록 반지름이 1이고, 길이가 1인 호(arc) 위의 점에 가까워지는 것을 알 수 있다.
그림 6. 식 (6)에서 n이 커질 수록 식 (6)의 값은 반지름이 1이고 길이가 1인 호(arc) 위의 점을 의미한다.
따라서 최종적으로 식 (6)이 의미하는 것은 무엇인가?
그것은 호도법(radian)의 의미를 생각해보면, 반지름이 1이고 각도가 1 라디안인 호 위의 점을 의미하게 된다.
그러면 $e^{i\theta}$는 어떻게 이해하면 좋을까?
그건 바로 반지름이 1이고 각도가 $\theta$ 라디안 인 호 위의 점을 의미하게 되며, 그것을 다른 수식으로 표현하면 바로 $\cos(\theta) + i\sin(\theta)$이다.
이런 방식으로 식(1)의 기하학적 의미를 이해할 수 있게 된다.
자연상수의 의미 -> 회전하며 성장
그렇다면 ‘성장’을 의미하는 자연상수 e의 본연의 의미를 여기선 어떻게 받아들일 수 있을까?
필자의 생각으로는 지금까지의 자연상수가 의미한 것은 동일한 방향으로 지속적으로 성장하는 것을 의미한 반면,
허수 지수가 들어가게 되면서 수직 방향으로 성장하게 되는 상황을 표현한 것으로 생각할 수 있을 것 같다.