행렬을 이용해 물체를 평행이동 시켜주는 변환은 수학적으로 어떻게 기술될 수 있을까?
Prerequisites
본 포스트를 잘 이해하기 위해선 아래의 내용에 대해 알고 오는 것이 좋습니다.
복습
벡터란 공간 상의 한 점으로 생각할 수 있다고 했다. 벡터를 표현할 때 위치와 방향성을 모두 고려하여 화살표로 나타낼 수도 있지만, 수 많은 벡터를 한번에 표시하기에는 너무 복잡해질 수 있으므로 위치만 표시하기도 한다.
그림 1. 벡터는 화살표로 표시하기도 하지만 점으로 표시할 수 있다.
만약 2차원 평면 상에 표시된 점들을 pixel로 생각한다면 벡터들의 나열을 그림으로 대체해 생각할 수도 있을 것이다.
2차원 공간에서의 선형 변환
행렬과 선형변환 편에서 배운 것 처럼 행렬은 하나의 선형 변환으로 표현할 수 있다. 그림에 선형 변환을 적용하면 기하학적으로 사진의 형태가 변형되기 때문이 기하 변환(geometric transformations)이라고도 부른다. 대표적인 변환들은 아래와 같다.
Scaling (2D)
\[\begin{bmatrix}2 & 0\\ 0& 1\end{bmatrix} % 식 (1)\]
그림 2. 2차원 공간의 scaling 변환
Shear (2D)
\[\begin{bmatrix}2 & 1\\ 1& 2\end{bmatrix} % 식 (2)\]
그림 3. 2차원 공간의 shear 변환
Rotation (2D)
\[\begin{bmatrix}\cos(\pi/3) & -\sin(\pi/3)\\ \sin(\pi/3)& \cos(\pi/3)\end{bmatrix} % 식 (3)\]
그림 4. 2차원 공간의 Rotation 변환
Permutation (2D)
\[\begin{bmatrix}0 & 1\\ 1& 0\end{bmatrix} % 식 (4)\]
그림 5. 2차원 공간의 Permutation 변환
3차원 공간에서의 선형 변환
선형 변환은 비단 2차원에만 해당하는 것이 아니며, 3차원에서도 적용할 수 있다. 아래는 3x3 행렬을 이용해 표현한 3차원 공간 상에서의 변환이다.
Scaling (3D)
\[\begin{bmatrix}2 & 0 & 0 \\ 0 & 1 & 0 \\ 0& 0&1\end{bmatrix}% 식 (5)\]
그림 6. 3차원 공간의 scaling 변환
Shear (3D)
\[\begin{bmatrix}2 & 1 & 0 \\ 1& 2 & 0 \\ 0& 0&1\end{bmatrix}% 식 (6)\]
그림 7. 3차원 공간의 Shear 변환
rotation (3D)
\[\begin{bmatrix}\cos(\pi/3) & -\sin(\pi/3) & 0 \\ \sin(\pi/3)& \cos(\pi/3) & 0 \\ 0 & 0 & 1\end{bmatrix} % 식 (7)\]
그림 8. 3차원 공간의 Rotation 변환
이 외에도 3차원 선형 변환이 동작하는 방식은 다양하므로 본 글의 맨 위에 있는 데모 애플릿을 이용해 3차원 선형 변환을 수행해보도록 하자.
아핀 변환 (Affine Transform)
평행이동을 하기 위해선 덧셈이 필요해
2차원 혹은 3차원에서의 변화에서 알 수 있는 점 중 하나는 나열되어 있는 변환들만으로는 평행이동을 표현하지 못한다는 것이다. 쉽게 말해, 그림을 상하좌우로 옮길 방법은 없어 보인다는 점이다. 그 이유는 일반적인 행렬의 곱만으로는 벡터 간의 덧셈을 표현할 수 없기 때문이다. 그러니까, 평행이동을 표현해주기 위해선 아래와 같이 덧셈 연산이 필요함을 생각할 수 있다.
\[\begin{bmatrix}x_{new} \\ y_{new} \end{bmatrix} =\begin{bmatrix}A_{11} & A_{12} \\ A_{21} & A_{22}\end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix} + \begin{bmatrix}b_1 \\ b_2\end{bmatrix} % 식 (8)\]위 식에서는 $\begin{bmatrix} x & y\end{bmatrix}^T$ 벡터에 선형변환을 적용한 뒤 $x$ 축으로 $b_1$, $y$ 축으로 $b_2$ 만큼 이동시키는 것을 알 수 있다. 참고로 수학에서 평행이동을 시켜주는 양을 “bias”라고도 표현하기도 하므로 $b$라는 알파벳을 활용했다.
행렬 하나만으로 평행이동을 표현하기 위한 방법
그런데, 만약 2차원 평면 상에 표현하는 벡터에 “bias”에 해당하는 차원을 하나 더 추가해주면 편리하게도 행렬의 곱셈 하나만으로 평행이동을 함께 표현할 수 있게 된다. 글로만 설명하면 무슨 말인지 이해하기 어려울 수 있기 때문에 수식을 같이 곁들이자면 아래와 같다.
\[\begin{bmatrix}x_{new} \\ y_{new} \\ 1\end{bmatrix} =\begin{bmatrix}A_{11} & A_{12} & b_1 \\ A_{21} & A_{22} & b_2 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix}x \\ y \\ 1\end{bmatrix} % 식 (9)\]즉, 식 (9)에서 벡터의 세 번째 차원은 실제로는 사용하지 않고 “bias 계산의 편의를 위해” 숫자 1로 도입하고 중간에 곱해지는 행렬도 $b_1$, $b_2$ 값을 오른쪽에 더 붙이고, 3행에는 [0, 0, 1]을 넣어 3x3 행렬을 구성하면 된다는 것이다.
이런 식으로 방향과 크기 뿐만 아니라 위치를 함께 포함하는 변환을 아핀 변환 (Affine transformation)이라고 부른다. 또, 식 (9)에서처럼 기존의 N 차원 벡터에 차원 하나를 덧붙여 표시하는 좌표계를 동차 좌표계(homogeneous coordinates)라고 부른다.
아핀 변환의 실체
아핀 변환을 처음 배웠을 때에는 다소 의아한 점이 많았다. 식 (8)의 비선형변환을 식 (9)와 같이 차원을 하나 늘려줌으로써 선형 변환처럼 서술할 수 있다는 것이 “교묘한 트릭”처럼 느껴졌다.
즉, 행렬과 선형변환에서 배운 것 처럼 선형변환은 원점을 보존해야 하는데, 아핀 변환의 존재는 내가 알고 있는 지식이 부실한 기반인냥 나를 기만하는 것 같기도 했다.
계산만 보면 차원을 하나 더 늘렸을 때 평행이동을 수학적으로 서술할 수 있다는 것은 알겠으나, 그렇다면 하나 더 늘린 차원은 어디에 존재한다는 말인가? 또, 하나 더 붙였던 차원은 그냥 떼버리는 것 처럼 사용하는데 아핀 변환은 선형변환의 관점에서는 이해할 수 없는 것일까? 속된말로 “야매” 수학일까? 아니면 충분히 실용적이기 때문에 사람들에게서 받아들여지고 있는 내용인 것일까? 등의 생각으로 정리가 어려웠다.
하지만, 아핀 변환은 한 차원 높은 좌표계에서의 선형 변환이 어떻게 일어나는지 생각할 수 있다면 그 정체를 이해할 수 있으며, 기존의 “선형 변환은 원점을 보존한다”는 지식도 그 기반을 단단하게 다질 수 있게 된다. 아래는 맨 위의 데모를 조감도로 본 것이다. 1행 3열의 값을 바꿔보면 무슨 일이 일어나는지 생각해보자.
1행 3열의 값을 양으로 변화시키면 3차원 공간에서는 정육면체 윗면이 오른쪽으로 밀리게 되지만, 조감도로 투영해보면 사진이 오른쪽으로 이동하는 것과 같은 효과를 가져오게 된다.
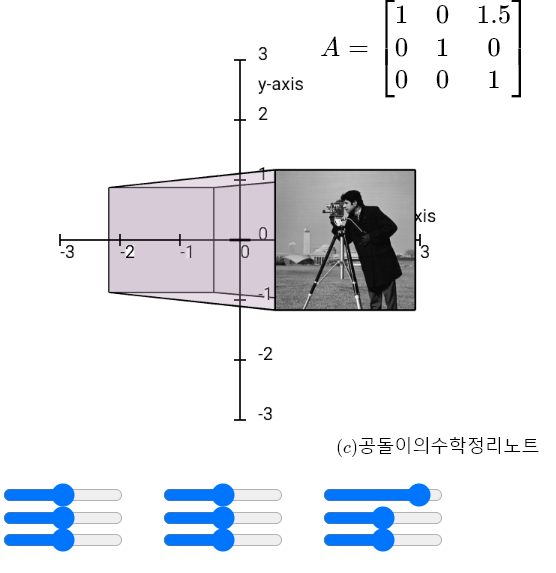
그림 9. 3차원 공간에서 1행 3열의 원소값 변화는 조감도로 보면 x축 상에서 평행이동해준 것과 같은 효과를 보인다.
마찬가지 방법으로 2행 3열의 원소값을 변화시키면 y축에서 평행이동하는 것과 같은 효과를 가져오게 된다.
즉, 아핀 변환에서 작용하는 행렬은 역시 원점을 보존해주는 변환임을 알 수 있으며, 추가된 하나의 차원에서 높이가 1인 지점에서의 변화를 관찰하여 2차원 평면에 투영하는 것과 같다는 것을 알 수 있다.