사비츠키-골레이(Savitzky-Golay) 필터

그림 1. smoothing 효과가 있는 Savitzky-Golay 필터! (진지)

Prerequisites

이번 포스팅을 이해하기 위해선 다음의 지식이 선행 학습되어야 합니다.

Discrete Time 신호의 Convolution
- Convolution 연산
- impulse response에 대한 개념
FIR 필터
행렬 연산에 관한 기초 지식 (행렬곱, 역행렬 등)

impulse response와 신호의 합성곱(convolution)

본 포스팅을 이해하기 위해선 impulse response에 대한 이해가 매우 필수적이다.

필요한 경우 짧게나마 impulse response에 대해 이해한 뒤, 해당 posting을 계속 읽어보도록 하자.

impulse response에 대한 이해가 충분하다고 생각된다면 이 파트는 건너뛰어도 무관하다.

임의의 이산신호 $x[n]$가 다음과 같은 형태의 신호라고 생각해보자.

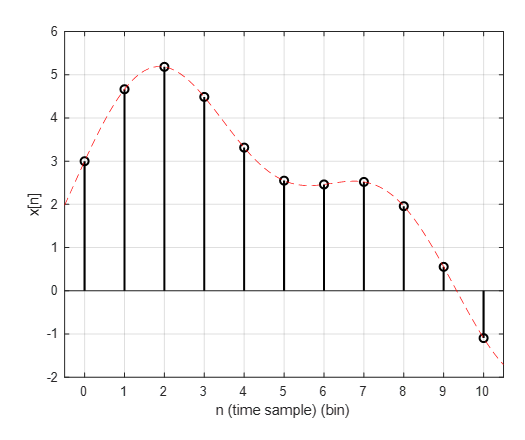
그림 2. 임의의 이산신호 $x[n]$

참고로 빨간색의 파선은 시간샘플링이 수행되기 전의 원래 함수라고 생각하면 될 것이다.

이 이산신호 $x[n]$은 모든 정수 $n$에 대한 $x[n]$값을 나열한 것이라고도 볼 수 있다. 그런데, 이 값들은 시간 순서대로 나와야 하므로, 아래 그림과 같이 각각의 함수 값($x[n]$)들을 가지는 impulse 들이 선형적으로 합해진 것으로도 볼 수 있을 것이다.

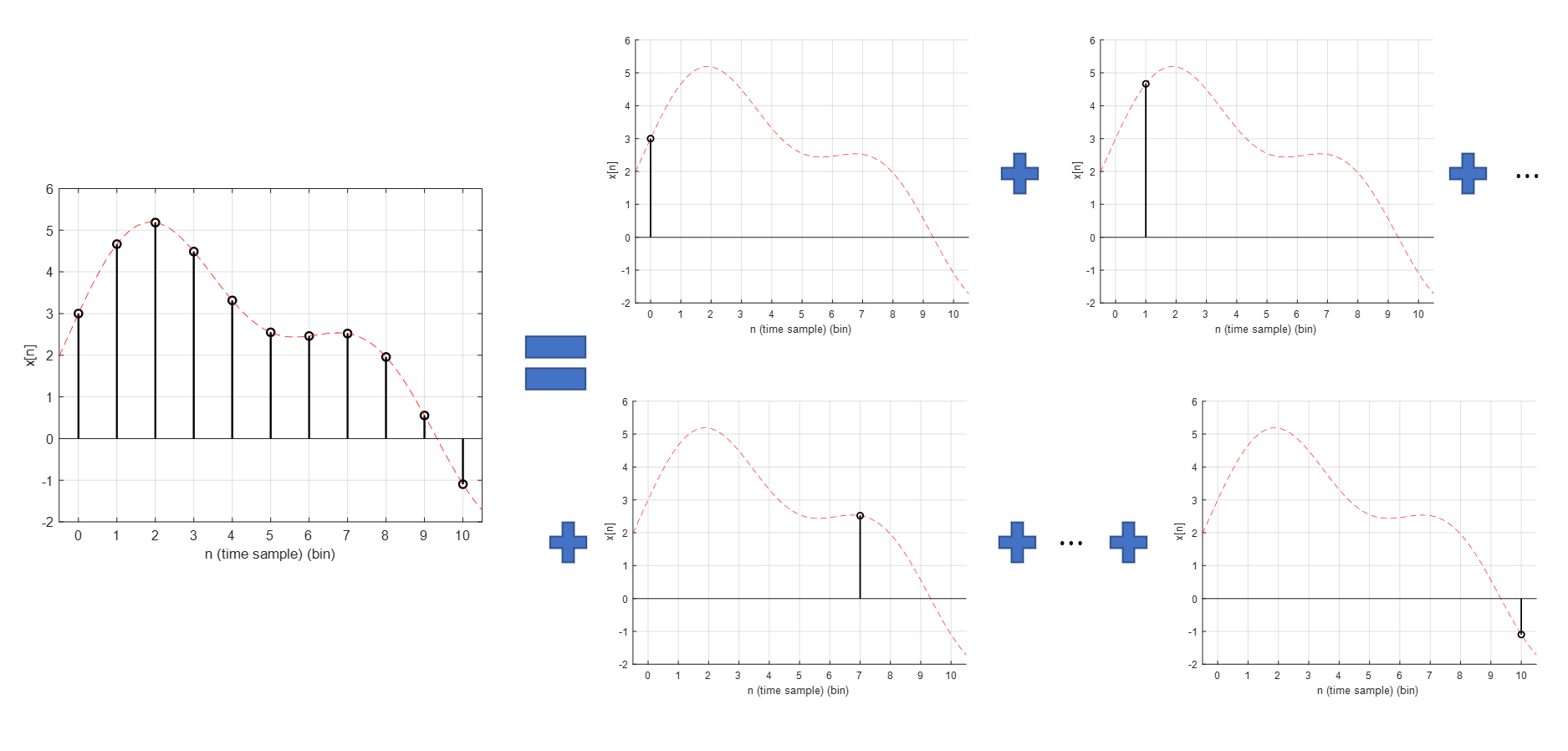
그림 3. 임의의 이산신호 $x[n]$

그림 3을 수식으로 표현하면 다음과 같다.

\[x[n] = \cdots + x[-2]\delta[n+2]+ x[-1]\delta[n+1] + x[0]\delta[n+0] + x[1]\delta[n-1] + + x[2]\delta[n-2]+\cdots\] \[=\sum_{k=-\infty}^\infty x[k]\delta[n-k]\]

여기서 $\delta[n]$은 아래와 같이 정의되는 함수이다.

\[\delta[n] = \begin{cases} 1 && \text{ if}\quad n = 0 \\ 0 && \text{otherwise } \end{cases}\]

여기서 우리가 어떤 선형 시스템을 생각한다고 하자. 이 시스템의 입력이 $x[n]$, 출력이 $y[n]$이라고 해보자. 출력과 입력의 관계를 연결시켜주는 선형시스템을 선형연산자 $O_n(\cdot)$로 대체해 생각한다면 입출력 관계는 다음과 같이 생각할 수 있다. (여기서 $O_n$의 아랫첨자 $n$은 이 연산자가 $n$에 대한 연산자라는 의미이다.)

\[y[n] = O_n(x[n])\]

식 (4)에 식 (1)을 대입하면,

\[\Rightarrow O_n\left(\sum_{k=-\infty}^\infty x[k]\delta[n-k]\right)\]

여기서 $O_n{\cdot}$은 $n$에 대한 선형연산자이므로 $x[k]$는 상수로 취급할 수 있다. 따라서,

\[\Rightarrow \sum_{k=-\infty}^{\infty}x[k]O_n\left(\delta[n-k]\right)\]

여기서 $O_n(\delta[n])$을 $h[n]$이라고 정의하자.

이 때 $h[n]$을 impulse response라고 부른다.

그러면,

\[\Rightarrow \sum_{k=-\infty}^{\infty}x[k]h[n-k]\]

만약 impulse response $h[n]$의 길이가 다음과 같이 유한하다고 생각해보자.

\[h[n] = \begin{cases} h[n] && \text{ if } -M\leq n \leq M \\ 0 && \text{otherwise} \end{cases}\]

그러면 다음과 같이 식 (7)의 $y[n]$을 쓸 수 있게 된다.

\[y[n] = \sum_{k=-M}^{M}x[k]h[n-k]\]

이렇듯 Impulse Response의 길이가 유한한 경우의 시스템을 Finite Impulse Response (FIR) 시스템이라고 한다.

다항 회귀 모델을 이용한 신호 스무딩(smoothing)

신호의 smoothing 방법에는 여러가지가 있다.

대표적인 smoothing 방법은 moving average로 시계열이 나열되어 있을 때 전체 데이터의 평균이 아니라 windowing을 통해 전체 데이터의 일부분을 순차적으로 평균을 구해서 평균값을 해당 윈도우의 대푯값으로 표시해 줌으로써 데이터를 smoothing 하는 방법을 말한다.

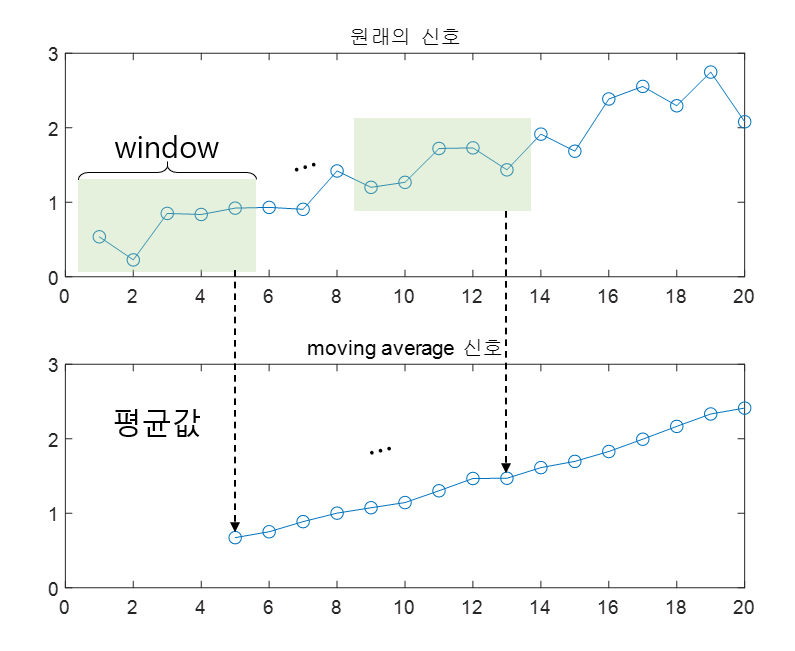
그림 2. moving average의 작동 원리

moving average를 취한다는 것은 아래와 같은 impulse response를 신호와 convolution 시켜준다는 것을 의미한다고도 생각할 수 있다. 가령 M차 moving average라면 impulse response는 다음과 같다.

\[h[n] = \begin{cases} 1/M && \text{ for } n = 0, 1, \cdots, M-1 \\ 0 && \text{otherwise} \end{cases}\]

여기서 moving average의 단점에 대해 금방 캐치할 수 있는 것은 moving average는 평균값을 이용한다는 점인데, 평균값은 outlier에 굉장히 취약하게 반응한다는 것이 잘 알려져 있다. 이런 이유로 어떤 application에서는 평균값 대신에 중위값(median)을 사용하는 경우도 왕왕 있다.

그래서 moving average는 구현이 쉽다는 장점이 있지만 순간적인 peak 등에 취약한 한계점을 보인다.

이를 보완하기 위한 방법 중 하나로 시계열에 적용시키는 window 내의 짧은 신호 구간에 대해 다항 회귀 모델을 구축함으로써 smoothing 하는 방법이 있을 수 있다.

그림 3. 다항 회귀모델을 이용한 신호의 smoothing 과정
그림 출처: 위키피디아 Savitzky Golay filter

위 그림에서는 짧은 구간의 window 내에서 다항 회귀모델을 만들어 신호를 smoothing하는 과정을 보여주고 있다.

아무리 다항회귀모델을 이용해서 신호를 smoothing 해준다는 것이 말인된다 한들 다항회귀모델을 이용한 smoothing의 경우 매 구간마다 회귀식을 계산해줘야한다는 매우 time-consuming한 과정일 것이고 매우 비효율적으로 보일지도 모르겠다.

Savitzky-Golay filter(S-G filter)는 이러한 회귀모델을 이용한 smoothing을 수행함에 있어 매 time step의 윈도우 내에서 회귀모델을 계산하지 않고도 특정한 impulse response를 마련함으로써 수학적으로 정확히 다항회귀모델을 이용한 smoothing을 대체할 수 있음을 말해주고 있다.

다시 말해, 적절히 계산된 impulse response를 이용하면 매 time step의 window 마다 회귀모델을 계산하는 것과 같은 효과를 얻을 수 있도록 필터를 설계할 수 있으며 이것이 S-G filter가 말해주고 있는 것이다.

유도 과정

지금부터 다루는 신호들은 모두 디지털 신호라고 가정하고, 시간 샘플을 앞으로 $n$이라고 표현하도록 하자.

우리가 원하는 것은 $-M\leq n \leq M$의 신호 $x[n]$을 적절한 $N$차 회귀모델 $p(n)=\sum_{k=0}^{N}a_kn^k$으로 대체하는 것이다.

즉, 회귀모델을 이용해 smoothing 하게되어 나오게 되는 신호 $p(n)$은 다음과 같다.

\[p(n) = a_0 + a_1 n+ a_2 n^2 + \cdots a_Nn^N\]

이게 무슨 말인가 하면, 시간 샘플 $0$을 중심으로 왼쪽으로 $-M$개, 오른쪽으로 $+M$개의 신호를 획득하고, 이 $2M+1$의 길이의 신호를 $N$차 회귀모델로 대체하겠다는 것이다.

굳이 시간 샘플이 $0$인 값을 중심으로 하는 신호에 대해 분석하고자 하는 것은 우리가 결국 하고 싶은 것은 회귀모델을 가지고 smoothing 해주려고 할 때 필요한 impulse response 이기 때문이다. impulse response를 이용해서 원래의 신호에 convolution을 해주면 결국 smoothing을 수행할 수 있다.

이제 이 $2M+1$ 길이의 신호를 모델링 해 줄 가장 적절한 회귀모델 $p(n)$은 아래와 같이 원래의 신호와의 에러를 가장 작게 해줄 수 있는 계수 $a_k \text{ where }k =0 ,1 ,\cdots, N$들로 구성될 것이다.

\[\epsilon_N = \sum_{n=-M}^{M}\left(p(n)-x[n]\right)^2\] \[=\sum_{n=-M}^{M}\left(\sum_{k=0}^Na_kn^k - x[n]\right)^2\]

편미분을 통해 에러를 최소화 할 수 있는 계수 $a_i\text{ for }i=0,1,\cdots,N$을 찾을 수 있다.

\[\frac{\partial\epsilon_N}{\partial a_i}=\sum_{n=-M}^{M}2\left(\sum_{k=0}^{N}a_kn^k-x[n]\right)n^i = 0\notag\] \[\text{ for }i=0,1,\cdots,N\]

위 식을 조금 더 정리하면,

\[\sum_{n=-M}^{M}n^i\sum_{k=0}^{N}a_kn^k-\sum_{n=-M}^{M}n^ix[n] = 0\] \[\Rightarrow \sum_{n=-M}^{N}\sum_{k=0}^{N}n^{i+k}a_k=\sum_{n=-M}^{M}n^ix[n]\]

이제 식 (15)를 행렬을 이용해 표현하기 위해 아래와 같은 행렬 $A$를 정의하자.

$(2M+1)\times(N+1)$의 dimension을 갖는 어떤 행렬 $A$를 다음과 같이 정의하도록 하자.

\[A = \lbrace a_{n, i} \rbrace = \lbrace n^i \rbrace\notag\] \[\text{where }-M\leq n \leq M \text{ and } i=0,1,\cdots,N\]

여기서 $\lbrace a_{n,i}\rbrace$의 표시는 $n$번째 행 $i$번째 열의 원소가 $n^i$와 같이 정의한다는 것을 의미한다.

참고로, 원소별로 쓰면 행렬 $A$는 다음과 같다¹.

\[A = \begin{bmatrix} (-M)^0 && (-M)^1 && \cdots && (-M)^N \\\\ (-M+1)^0 && (-M+1)^1 && \cdots && (-M+1)^N \\\\ \vdots && \vdots && \vdots && \vdots \\\\ 0^0 && 0^1 && \cdots && 0^N \\\\ 1^0 && 1^1 && \cdots && 1^N \\\\ \vdots && \vdots && \ddots && \vdots \\\\ M^0 && M^1 && \cdots && M^N \end{bmatrix}\]

또, 식 (15)를 행렬을 이용해 표현하기 위해 필요한 벡터들을 추가로 몇개 쓰자면,

\[\vec a = [a_0, a_1, a_N]^T\] \[\vec x = [x[-M], \cdots, x[-1], x[0], x[1], \cdots, x[M]]^T\]

이다.

이제 $A, \vec{a}, \vec{x}$를 이용해 식 (x)를 행렬로 쓰면 다음과 같다.

\[식(15)\Rightarrow A^TA\vec{a} = A^T \vec{x}\]

이 과정을 잘 이해하기 위해 $A^TA$를 계산해보면, $A^T$의 $i$번째 행, $A$의 $k$번째 열은 각각

\[A^T_{(i,:)}=[(-M)^i, (-M+1)^i, \cdots, M^i]\] \[A_{(:, k)} = [(-M)^k, (-M+1)^k, \cdots, M^k]^T\]

이므로, $A^TA$의 $i$번째 행, $k$번째 열의 원소는

\[A^TA = \lbrace a_{i,k}\rbrace = \left\lbrace \sum_{n=-M}^{M}(n)^{i+k}\right\rbrace\]

임을 알 수 있고, 또 $A^T\vec{x}$의 경우,

\[A^T\vec{x}= \begin{bmatrix} (-M)^0 && (-M+1)^0 && \cdots && 0^0 && 1^0 && \cdots && M^0 \\\\ (-M)^1 && (-M+1)^1 && \cdots && 0^1 && 1^1 && \cdots && M^1 \\\\ \vdots && \vdots && \vdots && \vdots && \vdots && \vdots && \vdots \\\\ (-M)^N && (-M+1)^N && \cdots && 0^N && 1^N && \cdots && M^N \end{bmatrix} \begin{bmatrix} x[-M]\\ \vdots \\ x[-1] \\ x[0] \\ x[1] \\ \vdots \\ x[M] \end{bmatrix}\] \[=\begin{bmatrix}\sum_{n=-M}^{M}n^0x[n] \\\\\sum_{n=-M}^{M}n^1x[n] \\\\ \vdots \\\\\sum_{n=-M}^{M}n^Nx[n]\end{bmatrix}\] \[=\sum_{n=-M}^{M}\begin{bmatrix}n^0 \\n^1 \\ \vdots \\ n^N \end{bmatrix}x[n]\]

임을 알 수 있다.

그러면 식 (20)을 통해 계수 벡터 $\vec{a}$를 계산할 수 있다².

\[\vec{a} = (A^TA)^{-1}A^Tx\]

그리하여 얻은 결과를 다음과 같이 정리하자.

\[(A^TA)^{-1}A^Tx = Hx\]

따라서, 첫 번째 계수 $a_0$는 다음과 같이 계산할 수 있을 것이다.

\[a_0 = H_{(1,:)}\cdot \vec{x}=\sum_{m=-M}^{M}h_{1, m}x[m]\]

여기서 $H_{(1,:)}$는 $H$의 첫 번째 행을 의미한다.

이제, 식 (29)에 대해 다시 한번 생각해보면 식 (29)는 결국 유한한 길이의 신호 $x[n] \text{ for } -M\leq n \leq M$에 대한 $n = 0$일 때의 출력값 $y[n]$과 같다는 것을 알 수 있다.

즉,

\[식 (29)\Rightarrow y_0 = a_0 = \sum_{m=-M}^{M}h[0-m]x[m]\]

이다. 식 (30)과 Finite Impulse Response를 갖는 시스템의 입출력에 관한 식인 식(9)를 비교해보면 결국 우리가 구한 $H$의 첫번째 행이 결국 Savitzky-Golay 필터의 impulse response라는 것을 알 수 있다.

MATLAB 코드

clear; close all; clc;

M = 10; % 필터의 길이는 2M+1 = 21
N = 9; % 다항식의 차수는 9

% 테스트용 신호
load mtlb
t = (0:length(mtlb)-1)/Fs;

%% MATLAB으로 계수만 얻은 것
b = sgolay(N, 2*M+1);

sgolay_filter = b((size(b,1)+1)/2,:);

smtlb = conv(mtlb, sgolay_filter,'same');

%% MATLAB으로 직접 convolution까지 한 것
smtlb_MATLAB = sgolayfilt(mtlb, N, 2*M+1);

%% 직접 S-G filter의 계수까지도 계산
A = zeros(2*M+1, N+1);

n_range = -M:M; % 원래 논문에서 n
i_range = 0:N; % 원래 논문에서 i
for i = 1:size(A,1)
    for j = 1:size(A,2)
        A(i,j)= n_range(i)^i_range(j);
    end
end

% matrix H = (A^TA)^{-1}*A^T

H = (A'*A)\A';

sgolay_filter_calculated = H(1,:); % H의 첫번째 행이 S-G filter의 impulse response이다.

my_smtlb_calculated = conv(mtlb, sgolay_filter_calculated,'same');

figure;
h1 = plot(t, mtlb);
axis([0.2 0.22 -3 2])
hold on;
% plot(t, smtlb);
h2 = plot(t, my_smtlb_calculated,'r', 'linewidth',2);
% plot(t, smtlb_MATLAB);
legend([h1, h2], '원형 파형','S-G filter 적용')

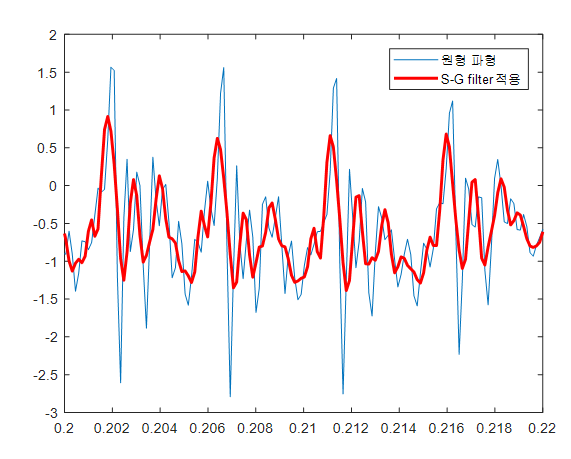
그림 4. 위 MATLAB 코드의 실행 결과