Prerequisites
본 포스트를 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것을 추천드립니다.
cyclic permutation matrix 소개
치환행렬은 행의 순서를 바꿔주는 행렬이다.
다만, 우리가 이번 post에서 이용할 치환행렬은 cyclic permutation을 수행해주는 행렬이다.
다시 말해, 어떤 벡터 $x$에 대해서,
\[\vec{x} = \begin{bmatrix}x_0\\x_1\\ \vdots \\ x_{n-1}\end{bmatrix}\]cyclic permutation을 수행해준다는 것은 다음과 같은 연산이 수행된다는 것을 말한다. permutation 행렬을 $P$라고 할 때,
\[P\vec{x} = \begin{bmatrix}x_{n-1}\\x_0\\ x_1 \\ \vdots \\ x_{n-2}\end{bmatrix}\]이러한 연산을 수행해주기 위해서는 다음과 같이 cyclic permutation 행렬이 정의되어야 한다.
\[P = \begin{bmatrix} 0 & 0 & \cdots & 0 & 1 \\ 1 & 0 &\cdots & 0 & 0 \\ 0 & \ddots &\ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & 0 \\ 0 & \cdots & 0 & 1 & 0 \end{bmatrix}\]즉, 대각성분 바로 아래의 성분들(준대각선)의 값이 1이고 행렬의 가장 우상단의 값이 1이 되어야 한다.
cyclic permutation 행렬의 재밌는 점은 $P$를 두 번 적용시켜주면 행이 두 번 shift 된다는 점이다.
다시 말해,
\[P\cdot P\vec{x} = P^2\vec{x} = \begin{bmatrix}x_{n-2}\\x_{n-1}\\ x_0 \\ \vdots \\ x_{n-1}\end{bmatrix}\]이다.
거기다가, $P^2$을 직접 써보면 다음과 같을 것이다.
\[P^2 = \begin{bmatrix} 0 & 0 & \cdots & 1 & 0 \\ 0 & 0 &\cdots & 0 & 1 \\ 1 & \ddots &\ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & 0 \\ 0 & \cdots & 1 & 0 & 0 \end{bmatrix}\]행을 $n$ 번 shift 시켜주기 위해선 $P$ 행렬을 $n$ 번 곱해줄 수 있다.
순환 행렬을 이용한 신호(벡터)의 분해
신호(벡터)의 분해를 생각하기 위해 신호의 분해의 기초가 되는 discrete unit sample function을 생각해보자. discrete unit sample function의 기호는 $\delta$로 쓰도록 하자.
\[\delta =\begin{bmatrix}1\\0\\ \vdots \\ 0\end{bmatrix}\]임의의 벡터에 대해서,
\[\begin{bmatrix}x_0\\x_1\\ \vdots \\ x_{n-1}\end{bmatrix} = x_0 \begin{bmatrix}1\\0\\ \vdots \\ 0\end{bmatrix} + x_1 \begin{bmatrix}0\\1\\ \vdots \\ 0\end{bmatrix} + \cdots + x_{n-1} \begin{bmatrix}0\\0\\ \vdots \\ 1\end{bmatrix}\]즉, 식 (7)이 말하는 것은 어떤 벡터라도 표준정규기저에 상수배해준 것의 합으로 표현해줄 수 있음을 말하고 있다.
한편, 식 (7)의 임의의 벡터 $x$는 discrete unit sample function $\delta$와 cyclic permutation matrix $P$를 이용해 다음과 같이도 쓸 수 있다.
\[= x_0 \delta + x_1 P\delta + x_2P^2\delta+\cdots x_{n-1} P^{n-1}\delta\]여기서 $\delta = I\delta$라고도 쓸 수 있으므로,
\[식 (8) \Rightarrow = x_0 I \delta + x_1 P\delta + x_2P^2\delta+\cdots x_{n-1} P^{n-1}\delta\] \[= \left(x_0 I + x_1 P + x_2P^2+\cdots x_{n-1} P^{n-1}\right)\delta\]이다.
여기서 $P$, $P^2$ 등의 행렬을 직접 써서 다시 식 (10)을 써보면,
\[\begin{bmatrix}x_0\\x_1\\ \vdots \\ x_{n-1}\end{bmatrix} = \begin{bmatrix} x_0 & x_{n-1} & \cdots & x_2 & x_1 \\ x_1 & x_1 &\cdots & x_3 & x_2 \\ x_2 & \ddots &\ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & x_0 & x_{n-1} \\ x_{n-1} & \cdots & x_2 & x_1 & x_0 \end{bmatrix} \begin{bmatrix}1\\0\\ \vdots \\ 0\end{bmatrix}\]과 같이 쓸 수 있음을 알 수 있다.
여기서 식 (11)에 $\delta$ 앞에 곱해진 행렬을 일반적으로 순환 행렬(circulant matrix) 이라고 부른다.
앞으로는 순환행렬의 기호는 $C$로 쓸 것이며 식 (11)을 일반화해서 다음과 같이 쓸 수 있다.
\[\vec{x} = C\delta=\left(\sum_{i=0}^{n-1}x_i P^{i}\right)\delta\]순환행렬과 이산컨볼루션의 관계
신호처리 이론에서 Kronecker delta 함수는 다음과 같이 정의된다.
\[\delta[n] = \begin{cases}1 && \text{ if }n=0 \\ 0 && \text{otherwise}\end{cases}\]
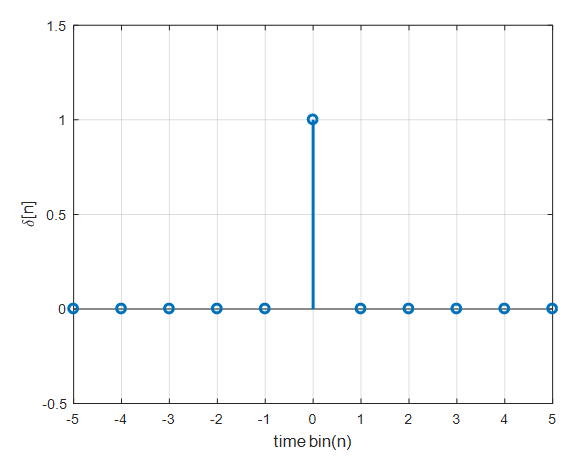
그림 1. 크로네커 델타 함수
우리는 크로네커 델타 함수를 이용해 임의의 이산 신호를 다음과 같이 분해할 수 있음을 알 수 있다.
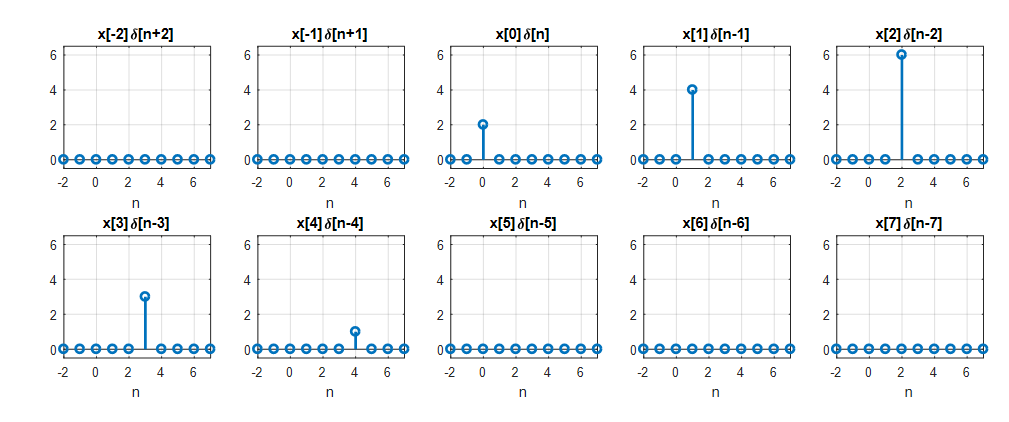
그림 2. 임의의 이산함수 $x[n]$는 크로네커 델타 함수를 이용해 분해해 생각할 수 있다.
이것을 수식으로 쓰면 아래와 같은데,
\[x[n]=\cdots + x[-2]\delta[n+2]+x[-1]\delta[n+1]+x[0]\delta[n]+x[1]\delta[n-1]+x[2]\delta[n-2]+\cdots\]또는 이렇게도 볼 수 있겠다.
\[x[n]=\cdots + x[n+2]\delta[-2]+x[n+1]\delta[-1]+x[n]\delta[0]+x[n-1]\delta[1]+x[n-2]\delta[2]+\cdots\]식 (15)는 다음과 같이 쓸 수 있다.
\[x[n] = \sum_{k=-\infty}^{\infty}x[n-k]\delta[k]\]이 식에 대해 $0\leq k \leq N-1$에 대해서만 생각해보면 다음과 같다.
\[x[n] = \sum_{k=0}^{N-1}x[n-k]\delta[k]\]$0\leq n \leq N-1$에 대해 식 (16)을 다시 풀어 쓰면,
\[x[0] = x[0]\cdot 1 + x[0-1]\cdot 0 + \cdots + x[0-(N-1)]\cdot 0\] \[x[1] = x[1]\cdot 1 + x[1-1]\cdot 0 + \cdots + x[1-(N-1)]\cdot 0\] \[\vdots \notag\] \[x[N-1] = x[N-1]\cdot 1 + x[(N-1)-1]\cdot 0 + \cdots + x[(N-1)-(N-1)]\cdot 0\]과 같이 쓸 수 있는데, 식 (18)에서 식 (20)까지를 모두 합쳐서 행렬로 표현하면 다음과 같이 쓸 수도 있다.
\[\begin{bmatrix}x[0]\\x[1]\\ \vdots \\ x[N-1]\end{bmatrix} = \begin{bmatrix} x[0] & x[N-1] & \cdots & x[1-(N-1)] & x[0-(N-1)] \\ x[1] & x[0] &\cdots & x[2-(N-1)] & x[1-(N-1)] \\ x[2] & \ddots &\ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & x[0] & x[N-1] \\ x[N-1] & \cdots & x[2] & x[1] & x[0] \end{bmatrix} \begin{bmatrix}1\\0\\ \vdots \\ 0\end{bmatrix}\]이 식을 생각할 때 $x[n]$이 $N$의 주기를 갖는 주기함수라 보면 이것은 식 (11)에서 본 circulant matrix로 표현한 벡터의 분해와 같은 것이라 할 수 있다.
결론적으로 circulant matrix를 이용해 벡터를 표현하는 것은 신호처리 이론에서 컨볼루션을 이용해 신호를 분해하는 것과 같은 일을 해주는 것이라 할 수 있다.