본 포스팅은 University of California Davis ENG 006: Engineering Problem Solving에서 제공하는 ZyBooks의 내용을 바탕으로 작성하였습니다.

연립방정식과 행렬

연립 방정식의 해

중학교 시절 배운 연립방정식 해법을 다시 한번 생각해보자.

가령 아래와 같은 연립 방정식을 생각해보자.

\[\begin{cases}2x+3y=1 \\ 4x + 7y=3\end{cases}\]

이 연립방정식의 해를 구하기 위해서는 위쪽 식과 아래쪽 식 중 하나에서 변수 하나를 소거해줘야 한다.

우리는 윗쪽 식에 2를 곱하고 아랫쪽 식에서 빼보자.

다시 말해, 윗쪽 식을 $r_1$이라고 하고 아랫쪽 식을 $r_2$라고 했을 때 아래와 같이 $r_2$를 새롭게 구성하는 것이다.

\[r_2 \rightarrow r_2 - 2 r_1\]

계산해보면,

\[4x+7y - 2(2x+3y)=3 - 2\times 1 = 1\] \[\Rightarrow (4x-4x)+(7y-6y)=y=1\]

임을 알 수 있다.

이 과정에서 우리는 $y=1$이라는 것을 알 수 있고, 이를 통해 첫 번째 식에 $y=1$을 대입함으로써,

\[2x+3(1)=1 \Rightarrow x = -1\]

임을 알 수 있다.

이 과정을 통해 알 수 있는 것은 연립 방정식을 풀 때는 두 가지 일을 해볼 수 있다는 것인데, 하나는 방정식 양변에 숫자를 곱하는 것과 또 하나는 방정식 두개를 합쳐주는 것이다.

또 한가지 추가적인 테크닉은 방정식 두 개의 순서를 서로 바꾸는 것도 문제가 되지 않을 것이라는 점이다.

요약하면 세 가지 스킬을 이용해 연립방정식을 풀 수 있다.

• 방정식의 양변에 숫자 곱해주기
• 서로 다른 방정식을 합쳐주기
• 서로 다른 방정식의 순서를 바꿔주기

행렬을 이용한 연립 방정식의 표현

그런데, 잘 생각해보면 행렬을 이용하면 연립 방정식을 표현해줄 수도 있다.

식 (1)의 연립 방정식은 아래와 같이 표현할 수 있다.

\[\begin{bmatrix}2 & 3 \\ 4 & 7\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}1\\3\end{bmatrix}\]

혹은 변수 $x,y$는 생략하고 아래와 같이 표현해주는 방법도 있다.

위의 행렬로 표현한 식에서

\[A=\begin{bmatrix}2 & 3 \\ 4 & 7\end{bmatrix}\]

라고 하고,

\[b = \begin{bmatrix}1\\3\end{bmatrix}\]

라고 하여 두 행렬을 양 옆으로 합친 행렬 $[A|b]$는

\[[A|b]=\left[\begin{array}{cc|c}2 & 3 & 1 \\ 4 & 7 & 3\end{array}\right]\]

와 같이 써줄 수도 있는 것이다. 이런 형태의 행렬을 첨가 행렬(augmented matrix)라고 한다.

첨가 행렬에서 긴 세로 막대기는 시각적 도움을 위한 보조선일 뿐 실제로는 일반 $2\times 3$ 행렬처럼 다뤄줘도 무방하다.

결론적으로 우리는 이 첨가 행렬의 각 ‘행(row)’들을 하나 하나의 방정식인 것 처럼 다7뤄줌으로써 연립 방정식을 풀 수 있게 된다.

그렇다면, 행렬로 연립방정식을 표현해줄 수 있다는 것 까지는 납득할 수 있지만, 굳이 더 복잡해 보이기만 하는 행렬로 연립 방정식을 표현해줘야 하는 이유가 있을까?

그 이유는 컴퓨터를 이용해 연립 방정식을 풀 수 있게 하려고 하는 것이다.

그러기 위해선 앞서 설명한 해를 구하기 위한 “세 가지 스킬들”에 대응되는 연산마저 컴퓨터로 표현할 수 있어야 한다.

행렬 곱에 대한 또 다른 시각 편에서 보았지만, 두 행렬을 곱한다는 것은 왼쪽의 행렬은 연산자의 기능을 하고, 오른쪽의 행렬은 피연산자의 기능을 하게 된다.

다시 말해, 임의의 행렬 $A$와 $B$에 대해 $AB$라는 연산에서 $A$는 연산을 수행해주는 역할, $B$는 연산을 받는 피연산 object의 기능을 한다는 것이다.

여기서도 마찬가지로 우리에게 주어진 $(A|b)$ 행렬에 대해 위에서 언급한 연립방정식의 스킬들을 적용하는 연산자 행렬을 생각해낼 수 있다면 이 행렬을 $(A|b)$ 행렬 앞에 곱해줌으로써 첨가 행렬의 행에 연산을 취해줄 수 있는 ‘기본 행 연산’을 수행해줄 수 있게 되는 것이다.

우리는 이렇듯 기본 행 연산을 수행해주는 연산을 기본 행렬(elementary matrix)라고 하며 이것은 기본 행 연산(elementary row operation)을 수행해주는 기능을 하는 행렬이라고 할 수 있다. 만약 이런 행렬들을 생각해낼 수 있다면 우리는 연립방정식을 푸는 과정을 컴퓨터를 통한 행렬 곱 연산으로 쉽게 해결해낼 수 있을 것이다.

Elementary matrices

연립방정식을 푸는 스킬에서부터 추측해보면 기본 행 연산(elementary row operation)은 총 세 가지라고 볼 수 있다.

• Row multiplication
• Row switching
• Row addition

기본 행렬의 역할은 뒤에 곱해질 행렬의 행에 연산을 취해주는 것이고, 가령 뒤에 곱해질 행렬의 크기가 $m\times n$이라면 기본 행렬의 크기는 $m\times m$이 되어야지만 뒤에 곱해질 행렬에 연산이 취해진 뒤에도 행렬의 크기는 그대로 유지될 수 있을 것이다.

그리고, 기본 행렬(elementary matrix)은 $m\times m$ 크기의 단위 행렬(identity matrix) $I_m$에서 숫자 하나만을 바꾸거나 행의 순서를 조작함으로써 얻을 수 있다.

무슨 말인지 각각의 연산에 대해 기본 행렬의 꼴을 생각해보도록 하자.

Row multiplication

row multiplication을 수행해주는 기본행렬은 아래와 같은 형태이다.

\[I=\begin{bmatrix}1&0&0\\0&1&0\\ 0&0&1\end{bmatrix} \rightarrow E=\begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{s} & 0 \\ 0 & 0 & 1\end{bmatrix}\]

즉, 단위 행렬(identity matrix)의 대각 성분 중 하나의 숫자를 바꿔서 얻게 되는 행렬이다.

위의 예시에서 보여준 행렬 $E$는 두 번째 대각 성분을 수정해서 상수 $s$로 바꿔주었는데, 이렇게 해주면 2번째 행에 상수배를 취해주는 연산을 해주게 된다.

기호로 표시하면 $r_2 \rightarrow sr_2$와 같으며, 임의의 $3\times 4$ 행렬 $A$에 행렬에 연산을 수행해주면 아래와 같은 연산이 수행되는 것이다.

\[EA = \begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{s} & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ \color{red}{a_{21}} & \color{red}{a_{22}} & \color{red}{a_{23}} & \color{red}{a_{24}} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix} =\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ \color{red}{sa_{21}} & \color{red}{sa_{22}} & \color{red}{sa_{23}} & \color{red}{sa_{24}} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix}\]

또, 추가로 생각해볼 수 있는 것은 row multiplication을 수행해주는 연산에 대한 역연산은 $1/s$ 배를 다시 수행해주는 것인데, 위와 같이 2행을 $s$배 해주는 연산에 대한 역연산은

\[E^{-1}=\begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{1/s} & 0 \\ 0 & 0 & 1\end{bmatrix}\]

와 같다는 것을 알 수 있으며, 이는 row multiplication 연산에 해당하는 기본행렬의 역행렬의 형태를 의미한다.

다시 말해,

\[EE^{-1}=E^{-1}E=I\] \[\Rightarrow \begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{s} & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{1/s} & 0 \\ 0 & 0 & 1\end{bmatrix}=\begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{1/s} & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{s} & 0 \\ 0 & 0 & 1\end{bmatrix}=\begin{bmatrix}1&0&0\\0&1&0\\ 0&0&1\end{bmatrix}\]

이라는 것이다.

Row switching

row switching은 단위 행렬의 행을 바꿔준 것으로 얻을 수 있다.

만약, 3행과 2행을 바꿔주는 연산을 수행하고자 한다면 다음과 같은 행렬을 생각해볼 수 있는 것이다.

\[I=\begin{bmatrix} 1 & 0 & 0 \\ \color{red}{0} & \color{red}{1} & \color{red}{0} \\\color{blue}{0} & \color{blue}{0} & \color{blue}{1}\end{bmatrix}\rightarrow P_{32}= \begin{bmatrix} 1 & 0 & 0 \\ \color{blue}{0} & \color{blue}{0} & \color{blue}{1}\\ \color{red}{0} & \color{red}{1} & \color{red}{0}\end{bmatrix}\]

기본 행렬 중 row switching을 해주는 행렬은 permutation matrix라고도 하고, symbol은 $P$를 쓴다. 거기에, 바꿔주는 행 두개의 번호를 $P_{ij}$와 같이 관례적으로 적어주어서 어떤 두 행의 순서를 바꾸고자 하는지를 명시해준다.

가령 임의의 $3\times 4$ 행렬에 $P_{32}$ 를 곱해주면 다음과 같은 결과로 이어지는 것이다.

\[P_{32}A=\begin{bmatrix} 1 & 0 & 0 \\ \color{blue}{0} & \color{blue}{0} & \color{blue}{1}\\ \color{red}{0} & \color{red}{1} & \color{red}{0}\end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ \color{red}{a_{21}} & \color{red}{a_{22}} & \color{red}{a_{23}} & \color{red}{a_{24}} \\ \color{blue}{a_{31}} & \color{blue}{a_{32}} & \color{blue}{a_{33}} & \color{blue}{a_{34}} \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ \color{blue}{a_{31}} & \color{blue}{a_{32}} & \color{blue}{a_{33}} & \color{blue}{a_{34}}\\ \color{red}{a_{21}} & \color{red}{a_{22}} & \color{red}{a_{23}} & \color{red}{a_{24}} \end{bmatrix}\]

또 추가로 생각해볼 수 있는 것은 행의 순서를 바꿔주는 기본 행렬(혹은 permuatation 행렬)의 역행렬은 자기 자신이라는 점이다. 이것은 꽤 자명해보이기도 하는데, 1행과 3행을 바꿔주는 연산을 다시 돌려 놓으려면 다시 1행과 3행을 바꿔주기만 하면 되는 것이다.

즉, 아래와 같은 행렬에 대해

\[P_{31}=\begin{bmatrix}0 & 0& \color{red}{1} \\ 0 & 1 & 0 \\ \color{blue}{1} & 0 & 0\end{bmatrix}\]

역행렬은

\[P^{-1}_{31}=\begin{bmatrix}0 & 0& \color{red}{1} \\ 0 & 1 & 0 \\ \color{blue}{1} & 0 & 0\end{bmatrix}\]

이다.

Row-addition matrices

마지막으로 생각해볼 기본 행 연산은 서로 다른 행끼리 더해주는 연산이다. 그리고, 더해준 결과를 어떤 행에 대체해두는 과정까지 수행해야 한다.

이 행위를 수식으로 표현하면 아래와 같은 것이다. 가령, 2행을 2행 더하기 1행의 $s$배로 바꿔준다는 것은 아래와 같은 결과를 얻는다는 것이다.

\[\begin{bmatrix} \color{blue}{a_{11}} & \color{blue}{a_{12}} & \color{blue}{a_{13}} & \color{blue}{a_{14}}\\ \color{red}{a_{21}} & \color{red}{a_{22}} & \color{red}{a_{23}} & \color{red}{a_{24}} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix} \rightarrow \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ \color{red}{a_{21}} \color{black}{+} \color{blue}{sa_{11}} & \color{red}{a_{22}} \color{black}{+} \color{blue}{sa_{12}} & \color{red}{a_{23}} \color{black}{+} \color{blue}{sa_{13}} & \color{red}{a_{24}} \color{black}{+} \color{blue}{sa_{14}}\\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix}\]

위와 같은 연산을 수행해주는 행렬 $E$를 생각해보자. 위 연산 전, 후 결과에 대해 연산이 이루어지기 전 행렬을 $A$라고 하면 다음과 같이 행렬 $E$가 행렬 $A$에 작동한다고 생각할 수 있다.

\[I=\begin{bmatrix}1 & 0 & 0 \\ \color{red}{0} & \color{red}{1} & \color{red}{0} \\ 0 & 0 & 1\end{bmatrix}\rightarrow E = \begin{bmatrix}1 & 0 & 0 \\ \color{red}{s} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\] \[EA=\begin{bmatrix}1 & 0 & 0 \\ \color{blue}{s} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix} \color{blue}{a_{11}} & \color{blue}{a_{12}} & \color{blue}{a_{13}} & \color{blue}{a_{14}}\\ \color{red}{a_{21}} & \color{red}{a_{22}} & \color{red}{a_{23}} & \color{red}{a_{24}} \\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix}=\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ \color{red}{a_{21}} \color{black}{+} \color{blue}{sa_{11}} & \color{red}{a_{22}} \color{black}{+} \color{blue}{sa_{12}} & \color{red}{a_{23}} \color{black}{+} \color{blue}{sa_{13}} & \color{red}{a_{24}} \color{black}{+} \color{blue}{sa_{14}}\\ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix}\]

이런 행렬 $E$가 어떻게 row-addition 연산을 수행해주는지 잘 생각해보자.

우선 생각해볼 수 있는 점은 행렬 $E$의 각 행을 이용해 수행하는 연산은 출력 행렬의 각 행에 영향이 간다는 것이다.

그림으로 생각해보면,

그림 1. 왼쪽에 곱해지는 행렬의 각 행은 출력으로 나오는 행렬의 각 행에 영향을 미치는 것이다.

그리고 왼쪽에 곱해지는 행렬 $E$의 각 행들의 각 원소는 피연산 당하는 행렬의 각 행들에 대해 얼마만큼 weight를 줄 것인가에 관한 것을 의미하기도 한다.

그림 2. 연산을 수행하는 행렬의 각 행에 들어있는 원소들이 말하는 것

따라서, 출력 행렬에 row addition 연산이 수행된다는 것은 아래와 같은 일이 일어나는 것이다.

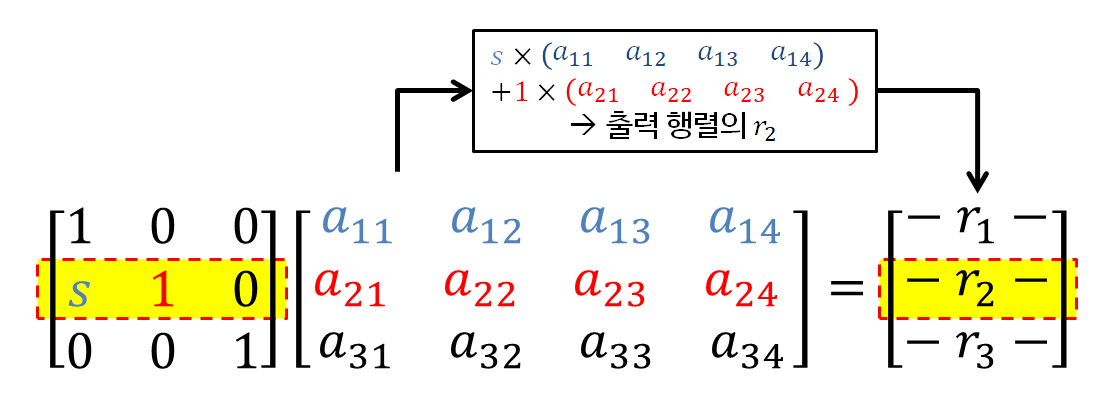
그림 3. 연산을 수행하는 행렬의 각 행에 들어있는 원소들이 말하는 것

이렇듯 row addition 연산을 이용하면 아래와 같이 특정 원소를 0으로 소거해줄 수 있다. 가령 아래와 같은 행렬 $A$에 대해,

\[A=\begin{bmatrix}\color{blue}{1} & 2 & 3 & 4 \\ \color{red}{1} & -1 & -2 & 2 \\ 0 & 3 & 2 & 1\end{bmatrix}\]

2행의 첫 번째 원소를 0으로 만들기 위해서 2행 = 2행 - 1행을 대입해주기 위해선 다음과 같이 기본행렬을 이용할 수 있다.

\[EA = \begin{bmatrix}1 & 0& 0\\ \color{blue}{-1} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}\color{blue}{1} & 2 & 3 & 4 \\ \color{red}{1} & -1 & -2 & 2 \\ 0 & 3 & 2 & 1\end{bmatrix}= \begin{bmatrix}\color{blue}{1} & 2 & 3 & 4 \\ \color{red}{0} & -3 & -5 & -2 \\ 0 & 3 & 2 & 1\end{bmatrix}\]

또 추가로 생각해볼 수 있는 것은 서로 다른 행끼리 더해주는 연산에 대한 역연산은 $-s$ 배해줘서 다시 더해주는 것이다.

가령, 아래와 같은 행렬에 대해

\[E=\begin{bmatrix}1 & 0 & 0 \\ \color{red}{s} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\]

역행렬은

\[E^{-1}=\begin{bmatrix}1 & 0 & 0 \\ \color{red}{-s} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\]

이다.

즉,

\[E^{-1}E=I\] \[=\begin{bmatrix}1 & 0 & 0 \\ \color{red}{-s} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 0 \\ \color{red}{s} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\]

이라는 점을 생각해볼 수 있다는 것이다.

기본행렬을 이용한 연립 방정식의 풀이

우리는 맨 처음에 보았던 연립방정식을 기본 행렬을 이용해 풀어보고 MATLAB으로 직접 implement하여 결과를 확인해보도록 하자.

\[\begin{cases}2x+3y=1 \\ 4x + 7y=3\end{cases}\] \[[A|b]=\left[\begin{array}{cc|c}2 & 3 & 1 \\ 4 & 7 & 3\end{array}\right]\]

두 번째 식의 $x$에 관한 항을 제거해 주기 위해 다음과 같은 연산을 수행하자.

\[r_2\rightarrow r_2 - 2r_1\]

그러기 위해 row addition 연산을 수행해보자. 그러기 위해 아래와 같은 기본행렬을 위의 첨가 행렬의 왼편에 곱해보자.

\[E_1=\begin{bmatrix}1&0\\-2&1\end{bmatrix}\] \[\Rightarrow E_1[A|b]=\begin{bmatrix}1&0\\-2&1\end{bmatrix}\left[\begin{array}{cc|c}2 & 3 & 1 \\ 4 & 7 & 3\end{array}\right]\] \[=\left[\begin{array}{cc|c}2 & 3 & 1 \\ 0 & 1 & 1\end{array}\right]\]

이번엔 첫 번째 행의 두 번째 원소 $3$을 없애주기 위해 아래와 같은 연산을 수행해보자.

\[r_1\rightarrow r_1 - 3r_2\]

그러기 위해 아래와 같은 기본 행렬을 곱해보자.

\[E_2=\begin{bmatrix}1&-3\\0&1\end{bmatrix}\] \[\Rightarrow \begin{bmatrix}1&-3\\0&1\end{bmatrix}\left[\begin{array}{cc|c}2 & 3 & 1 \\ 0 & 1 & 1\end{array}\right]=\left[\begin{array}{cc|c}2 & 0 & -2 \\ 0 & 1 & 1\end{array}\right]\]

마지막으로 첫 행을 1/2배 해주자. 그러기 위해 아래와 같은 기본행렬을 곱해보자.

\[E_3 = \begin{bmatrix}1/2&0\\0&1\end{bmatrix}\] \[\Rightarrow \begin{bmatrix}1/2&0\\0&1\end{bmatrix} \left[\begin{array}{cc|c}2 & 0 & -2 \\ 0 & 1 & 1\end{array}\right] =\left[\begin{array}{cc|c}1 & 0 & -1 \\ 0 & 1 & 1\end{array}\right]\]

따라서, $x=-1$, $y=1$ 임을 마지막 결과 첨가행렬을 통해 확인할 수 있는 것이다.

그리고 이 과정을 잘 생각해보면 아래와 같이 기본 행렬들 $E_1$, $E_2$, $E_3$을 차례대로 써서 결과를 얻을 수 있다는 것도 알 수 있다.

\[E_3E_2E_1[A|b] =\begin{bmatrix}1/2&0\\0&1\end{bmatrix} \begin{bmatrix}1&-3\\0&1\end{bmatrix} \begin{bmatrix}1&0\\-2&1\end{bmatrix} \left[\begin{array}{cc|c}2 & 3 & 1 \\ 4 & 7 & 3\end{array}\right] =\left[\begin{array}{cc|c}1 & 0 & -1 \\ 0 & 1 & 1\end{array}\right]\]

그리고 컴퓨터로는 아래와 같이 간단한 코딩으로 연산들과 방정식을 표현하고 해를 얻을 수 있게 된다.

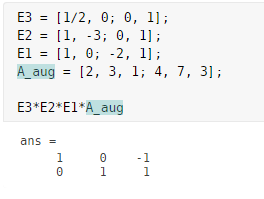
그림 4. 기본 행렬을 이용한 연립방정식의 풀이 (MATLAB)