미소곡면의 법선벡터

이번 article에서는 벡터장의 면적분을 이해하기 위해 필수적인 미소 곡면의 법선 벡터에 대해서 알아보고자 한다.

이를 위해서 우리는 곡면의 수학적 표현에 대해 이해하고자 한다.

매개변수 하나로 표현하는 곡선의 방정식

매개변수 방정식은 일반적으로 다음과 같이 표현할 수 있다.

매개변수 $t$에 대하여,

\[r(t) = \begin{bmatrix}x(t)\\y(t)\end{bmatrix}=x(t)\hat{i}+y(t)\hat{j}\]

고등학교 수학 시간에 배우기는 하지만 매개변수를 이용해 표현하는 직선(혹은 곡선)의 방정식은 한 눈에 이해하기가 어려웠던 것 같다.

그 이유는 우리가 보통 그리는 함수들은 입력과 출력을 한 평면에 모두 나타내게 되므로 (보통 입력을 $x$축에, 출력을 $y$축에 표현한다.) 입력이 변할 때 출력이 어떻게 변하는지 한눈에 알 수 있었기 때문이다.

그러나, 매개변수를 이용해 표현한 방정식은 그 결과만을 볼 때 함수의 출력만을 관찰하게 되기 때문에 그 결과물을 한눈에 이해하기 힘들다.

따라서 매개 변수를 이용해 표현한 직선(혹은 곡선)의 방정식을 조금이나마 쉽게 이해해보려면 입력의 변화와 출력의 변화를 한꺼번에 나타낼 수 있어야 할 것이다.

실생활에서 사용되고 있는 매개 변수를 이용해 표현한 직선의 방정식은 바로 스크롤이다.

그림 1. 스크롤의 위치를 이용해 현재 보여줄 페이지의 위치를 현재 화면에 매핑해 표현해주고 있다.

그림 1에서처럼 스크롤을 이동하게 되면 현재 스크롤의 위치에 맞게 매핑된 보고싶은 위치의 화면이 출력되게 된다.

즉, 스크롤은 여기서 매개 변수의 정의역에 해당하며 현재 보이는 화면의 위치가 치역에 해당된다고 할 수 있다.

이와 같이 매개변수의 정의역과 함수의 결과값인 치역을 한번에 나타내는 방식으로 조금 더 복잡한 함수를 표현해보자.

아래의 applet은 매개 변수 $t$를 이용해 표현한 함수 $r(t)$이다.

\[r(t) = \begin{bmatrix} t\cdot \cos(2\pi t) \\ t\cdot \sin(2\pi t)\end{bmatrix}\]
t로 매개된 곡선의 매개변수 방정식

위 applet을 보면 $t = 0$일 때 부터 $t = 3$일 때 까지의 변화가 슬라이더 상에 표현되고, 그 결과들이 각 $t$의 변화에 따라 매핑되는 것을 알 수 있다.

매개 변수를 이용해 표현한 곡선의 접선

또한, 매개변수를 이용해 표현한 곡선은 다른 함수들처럼 미분계수를 구할 수도 있다.

아래는 $t$의 변화에 따른 접선 벡터의 변화를 표시한 것이다.

t로 매개된 곡선의 매개변수 방정식의 접선 벡터

매개 변수의 접선 벡터를 수식으로 표현하면 다음과 같은데,

\[r'(t) = \begin{bmatrix} dx / dt \\ dy/dt\end{bmatrix}\]

이 말인 즉슨, 매개 변수 $t$가 약간 변할 때 $x(t)$와 $y(t)$는 각각 얼마나 변하는가를 말하고 있다.

매개 변수 두 개를 이용해 표현하는 곡면의 방정식

그렇다면, 곡면의 방정식을 표현하기 위해선 어떻게 해야할까?

일반적으로 곡면의 방정식은 매개변수가 두 개 필요하다.

매개변수를 이용한 곡면의 방정식은 일반적으로 다음과 같이 쓸 수 있다.

\[r(u, v) = \begin{bmatrix}x(u,v) \\ y(u,v) \\ z(u,v) \end{bmatrix} = x(u,v)\hat{i} + y(u,v)\hat{j} + z(u,v)\hat{k}\]

곡선에 대해 이해할 때와 마찬가지로 정의역과 치역을 각각 따로 놓고 곡면을 표현해보면 아래 그림과 같다.

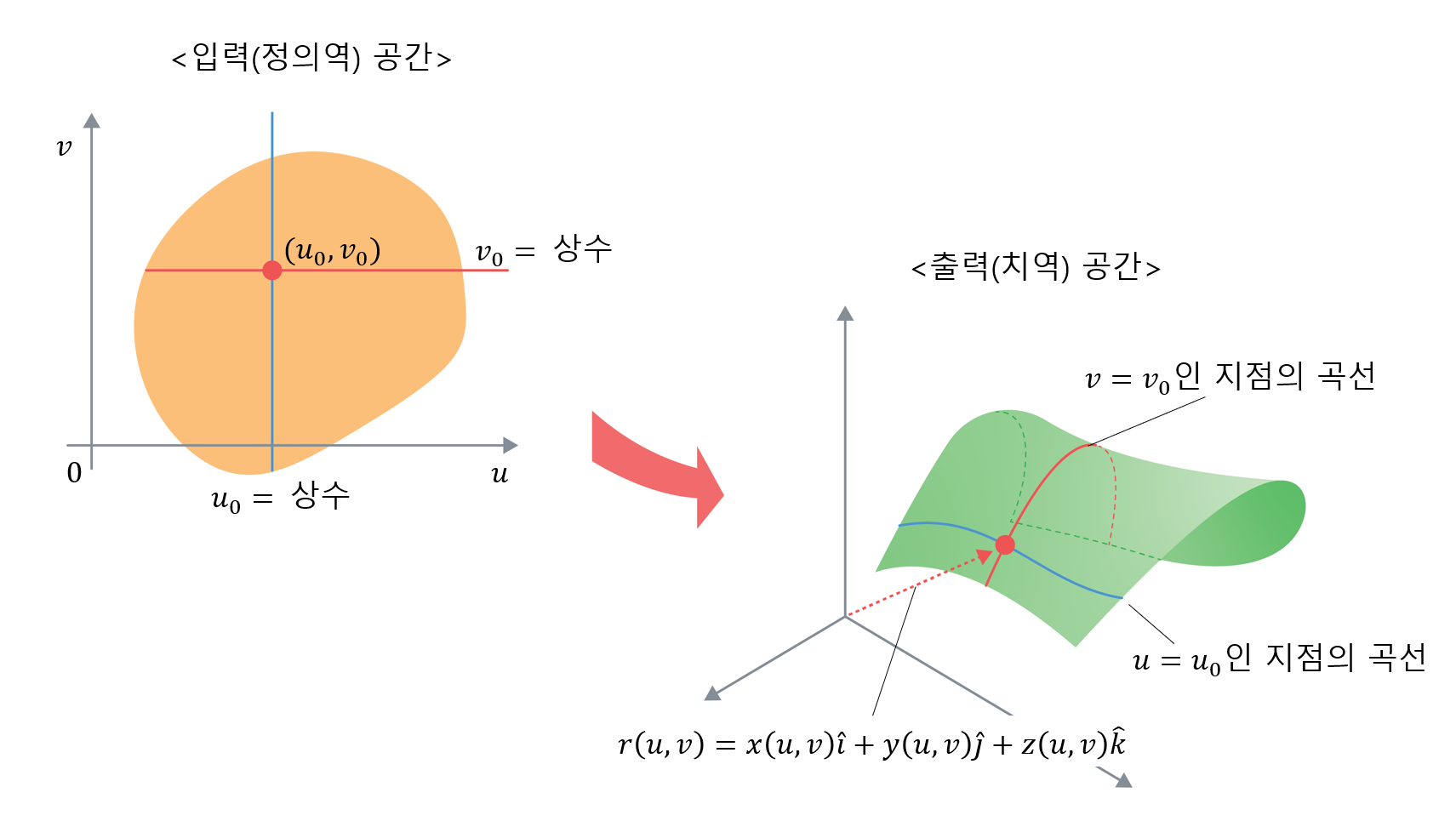
그림 2. 매개 변수를 이용해 표현한 곡면의 입력 공간과 출력 공간

우선, 곡면의 방정식은 $u$와 $v$로 표현한 두 개의 매개 변수가 이용되므로 입력 공간(정의역)은 2차원 벡터 공간으로 생각할 수 있다.

이 때, 출력 공간(치역)에서는 $u$와 $v$가 변함에 따라 출력 함수 $r(u, v)$의 값이 결정되게 되므로 3차원 벡터 공간 상에서의 위치가 결정되게 된다.

특히 주목할 점은 입력 공간에서 $u$ 혹은 $v$를 상수로 놓으면 출력 공간에서는 하나의 곡선이 결정되게 된다는 점이다.

매개 변수를 이용해 표현한 곡면의 접평면과 법선벡터

매개 변수를 이용한 방정식으로 곡면을 하나 결정할 수 있게 된다고 하였을 때, 입력 공간에서의 $u$ 혹은 $v$ 방향으로의 미세한 변화 $du$ 혹은 $dv$는 출력 함수 $r$의 작은 변화 $dr$을 이끌어 내게 된다.

가령, $u$에 대한 작은 변화가 $r$에서 일으키는 작은 변화 $dr$을 생각해볼 때 $v$를 상수로 두고 오직 $u$만을 변화시켰을 때 $r$에서는 얼마만큼의 변화가 일어나는지에 대해 생각해볼 수 있다. 이는 그림 1에서 본 것과 같이 곡면 상에 있는 곡선의 접선벡터를 구하는 과정과 같으며, 편미분의 개념이 그대로 적용된 것으로 볼 수 있다.

따라서 편미분 기호를 이용해 이러한 변화의 비율을 수식으로 쓰면 각각 다음과 같다.

\[u\text{의 작은 변화에 따른 } r\text{의 변화율 }\Rightarrow \frac{\partial r}{\partial u} = r_u\] \[v\text{의 작은 변화에 따른 } r\text{의 변화율 }\Rightarrow \frac{\partial r}{\partial v} = r_v\]

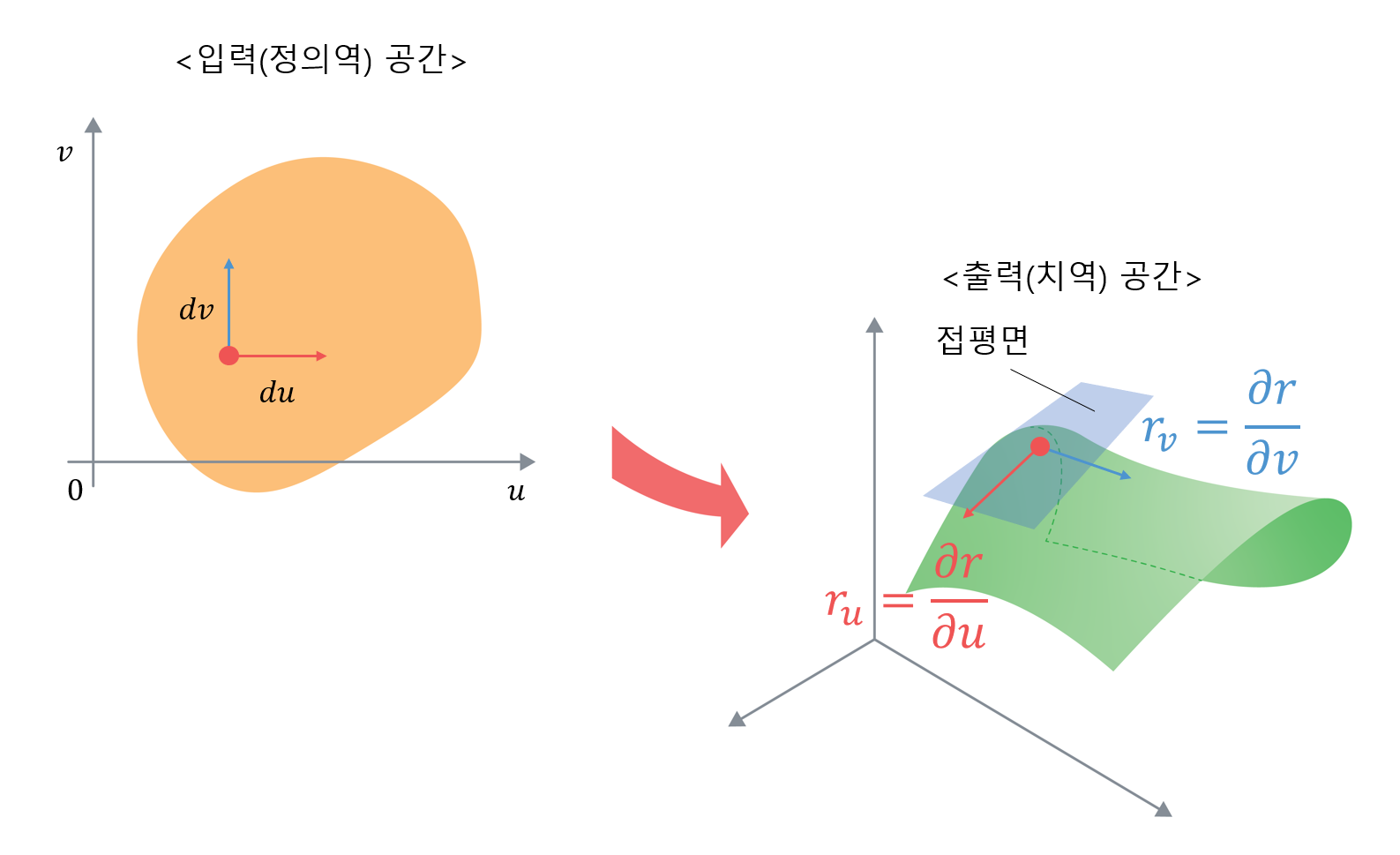
그림 3. 입력 공간의 작은 변화에 따라 얻어지는 출력 공간에서의 변화율