Prerequisites
이 포스팅의 내용을 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것을 추천합니다.
ANOVA를 생각하는 또 다른 관점
분산분석을 공부할 때 있어서 제곱합이라는 개념이 가장 큰 걸림돌이 된다. 처음 들으면 다소 생소한 개념일 수 있으나 제곱합의 개념은 분산 분석에서 아주 중요한 개념이다. 일단은 제곱합을 왜 사용해야 할까?
보통 분산 분석에서 제곱합이라고 하는 것은 좀 더 정확히 쓰자면 편차 제곱합(sum of squares of difference)라고 쓰는 것이다. 이 이름을 보면 우리가 생각해봐야 하는 것은 두 가지이다. 왜 편차에 관심을 가져야 하고 제곱합에 관심을 가져야 할까?
우선, 편차에 대해 생각해보자. 어떤 비교든지 간에 비교의 시작은 빼기(-)를 수행해줘야 비교할 수 있다. 그렇게 어려울 것이 없다. 비교를 위해서 편차를 생각하는 것은 자연스러운 논리적 흐름이라고 할 수 있다.
그럼 제곱은 왜 해줄까? 우선은 부호를 제거해주기 위한 목적이 있다. 편차는 양수, 음수 모두 나올 수 있기 때문에 합해주는 과정에서 복잡함이 생긴다. 절대값을 씌워줄 수도 있지만 그것보다는 제곱을 취하는 편이 계산에 편리하다. 따라서, 부호에 관계 없이 ‘변동’의 의미만을 남기고자 하는 것이다.
그런데, 제곱합을 이용하는 것이 끝까지 살아남은 이유는 전체 제곱합은 특별한 의미를 지닌 제곱합들로 쪼개 생각할 수 있기 때문이다. 무슨 말인지 감이 오지 않을텐데, 뒤에서 더 설명할 “ANOVA를 SS 관점에서 이해해보기”를 들여다보면 더 깊게 이해할 수 있을 것이다.
이 시점부터는 제곱합을 SS(Sum of Squares)라고 줄여 적도록 하겠다.
용어 정리
SS를 이용해 ANOVA를 이해해보기에 앞서 용어를 미리 정리하고 넘어가도록 하자.
처음보는 용어들이기 때문에 계속해서 이 부분을 참고해가면서 이해한다면 도움이 될 것이라 믿는다. 각 용어에 대한 자세한 설명은 아래의 유도 과정을 따라가면서 붙여나갈 것이다.
-
$SS_\text{something}$이라고 쓰면 something에 의해서 설명되는 제곱합이다.
-
자유도(degree of freedom; DF)는 주어진 조건 안에서 통계적인 추정을 할 때에 표본이 되는 자료 중에 모집단에 대한 정보를 주는 독립적인 자료의 수를 말한다.
$DF_\text{something}$이라고 쓰면 something이라는 조건에 관한 자유도를 말한다.
-
평균 제곱(mean square; MS)은 SS의 평균으로써, 산술적 평균이 아니라 SS를 자유도로 나눈 값이다.
즉, 평균적인 편차라는 의미에서 일종의 분산 역할을 한다. 다만 분산과 개념을 구분시켜 생각하는 이유는 MS는 여러가지 이유로 자유도가 수정되면 수정될 수 있는 통계치이기 때문이다.
One-way ANOVA를 SS의 관점에서 이해해보기
우리는 F-value의 의미와 분산분석 편에서 분산분석을 수행하는 과정을 확인해보았다.
분산분석은 기본적으로 모든 샘플 집단이 하나의 모집단에서 나왔다는 귀무가설을 가지고 진행된다.
그리고 ANOVA에서는 이 귀무가설을 확인하기 위해 두 가지 방법으로 분산을 추정한다. 첫 번째는 각 샘플 집단들이 가지고 있는 분산값을 이용하는 것이고 두 번째는 각 샘플 그룹의 평균값들이 퍼진 정도를 이용해서 분산을 추정하는 것이다. 만약 집단 내의 분산에 비해 샘플 집단 평균 간의 분산이 너무 크다면 우리는 귀무가설이 맞기 어려울 것이라고 보고 귀무가설을 기각해 적어도 하나의 샘플 집단은 다른 모집단에서 추출되었을 것이라고 볼 수 있다고 했다.
이 때, 분산의 비율값을 F 값이라고 불렀다. 즉, F 값을 수식으로 쓰면,
\[F=\frac{s^2_\text{bet}}{s^2_\text{wit}}\]이다. 여기서
\[s^2_\text{bet}\]는 그룹들의 평균값을 이용해 추정한 분산값,
\[s^2_\text{wit}\]는 각 그룹 내 표준오차를 이용해 추정한 분산값 말한다.
F 값의 확률 분포는 잘 알려져 있기 때문에 주어진 샘플 그룹으로부터 계산한 F 값이 얼마나 상대적으로 큰 값인지 계산할 수 있는 것이고 이를 통해 통계적 유의성을 검증한다.
(만약 위 내용이 잘 이해되지 않는다면 F-value의 의미와 분산분석 편을 보시는 것을 추천드립니다.)
F-value의 의미와 분산분석 수행해보았던 계산을 다시 한번 수행해보자.
다만, SS를 이용해서 ANOVA의 계산식을 새롭게 써보려고 하기 때문에 이전 ANOVA 포스팅의 내용에 비해 계산 과정은 훨씬 더 복잡할 것이다. 같은 결과를 얻기 위해 이런 복잡한 과정을 거치는 일이 꼭 필요한가 싶겠지만, 좀 더 복잡한 조건을 갖는 ANOVA를 수행하기 위해선 이런 과정은 불가피하다고 할 수 있다.
주어진 데이터 셋은 아래와 같이 표로 정리된 값으로 생각해보도록 하자.
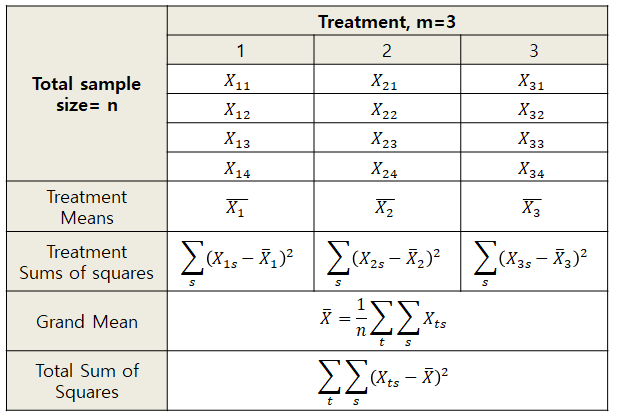
그림 1. 분산분석에 사용되는 데이터를 표와 기호로 정리한 것
그룹 내 분산($s^2_\text{wit}$)은 각 treatment 그룹 별 분산을 평균낸 것으로 볼 수 있다고 하였으므로1 다음과 같이 계산할 수 있는 값이다. 각 treatment 그룹의 분산을 $s_1^2, s_2^2, s_3^2$ 등이라고 한다면 아래와 같이 계산될 수 있다.
\[s^2_\text{wit}=\frac{1}{3}\left(s_1^2 + s_2^2 + s_3^2\right)\] \[=\frac{1}{3}\left( \frac{\sum_s\left(X_{1s}-\bar{X}_1\right)^2}{n-1} + \frac{\sum_s\left(X_{2s}-\bar{X}_2\right)^2}{n-1} + \frac{\sum_s\left(X_{3s}-\bar{X}_3\right)^2}{n-1} \right)\]여기서
\[SS_1 = \sum_s\left(X_{1s}-\bar{X}_1\right)^2\] \[SS_2 = \sum_s\left(X_{2s}-\bar{X}_2\right)^2\] \[SS_3 = \sum_s\left(X_{3s}-\bar{X}_3\right)^2\]와 같이 써주면, (여기서 아랫첨자 $s$는 subject, $t$는 treatment를 의미할 것이다.)
그룹 내 분산 값은
\[s^2_\text{wit}=\frac{1}{3}\left( \frac{SS_1}{n-1} + \frac{SS_2}{n-1} + \frac{SS_3}{n-1} \right)\]과 같고, 조금 더 요약해보면,
\[s^2_\text{wit}=\frac{1}{3}\left( \frac{SS_1+SS_2+SS_3}{n-1} \right)=\frac{\sum_t SS_t}{3(n-1)}=\frac{\sum_t \sum_s\left(X_{ts}-\bar{X}_t\right)^2}{3(n-1)}\]과 같다. 여기서 $SS_1+SS_2+SS_3$이 각 treatment 그룹 내에서 평균으로부터 각 샘플값이 떨어진 정도의 제곱합을 의미하므로 $SS_\text{wit}$라고 쓰자. 그리고 각 그룹별 표본의 개수는 $n$개, 그룹의 수는 $m$개라고 한다면,
\[s^2_\text{wit}=\frac{SS_{wit}}{m(n-1)}=\frac{SS_\text{wit}}{DF_\text{wit}}\]과 같다. 그러므로 그룹 내 분산 값은 $SS_\text{wit}$을 자유도 $DF_\text{wit}=m(n-1)$로 나눈 값과 같다는 것을 알 수 있다.
그렇다면 이번에는 그룹 간 분산을 생각해보자. 우리는 각 그룹의 평균값을 알고 있기 때문에 각 그룹의 평균값이 갖는 표준 오차를 생각해볼 수 있다.
\[s^2_{\bar{X}}=\frac{s^2_\text{bet}}{n}\]여기서 $S_{\bar{X}}$는 각 treatment 평균이 퍼진 정도, 즉 표준 오차를 얘기한다.
그러므로,
\[s^2_{\bar{X}} = \frac{(\bar{X}_1-\bar{X})^2+(\bar{X}_2-\bar{X})^2+(\bar{X}_3-\bar{X})^2}{m-1}\] \[=\frac{\sum_t(\bar{X}_t-\bar{X})^2}{m-1}\]임을 알 수 있다. 한편 식 (12)를 살짝만 틀어서 생각해주면
\[s^2_\text{bet}=ns^2_{\bar{X}}\]이므로,
\[s^2_{\text{bet}}=\frac{n\sum_t(\bar{X}_t-\bar{X})^2}{m-1}\]과 같이 $s^2_{\text{bet}}$을 계산할 수 있다는 점을 알 수 있으며, 더군다나 분자의
\[n\sum_t(\bar{X}_t-\bar{X})^2\]이라는 식이 가져다주는 의미가 grand mean $\bar{X}$로부터 각 treatment의 평균값이 떨어진 정도라는 것을 알 수 있다. 그리고 m개의 그룹으로부터 분산을 계산할 때의 자유도는 m-1이다는 사실 또한 생각할 수 있다. 그러므로,
\[s^2_{\text{bet}}=\frac{n\sum_t(\bar{X}_t-\bar{X})^2}{m-1}=\frac{SS_\text{bet}}{DF_\text{bet}}\]과 같이 $s^2_{\text{bet}}$을 SS를 이용해 써볼 수 있다는 점 또한 알 수 있다.
자, 지금까지 알아본 SS를 정리해보면 다음과 같이 정리할 수 있다.
\[SS_\text{wit}=\sum_t\sum_s\left(X_{ts}-\bar{X}_t\right)^2\] \[SS_\text{bet}=n\sum_t\left(\bar{X}_t-\bar{X}\right)^2\]그리고 마지막으로 우리는 각 샘플들이 grand mean $\bar{X}$로부터의 편차 제곱합인
\[SS_\text{tot}=\sum_t\sum_s\left(X_{ts}-\bar{X}\right)^2\]을 생각할 수도 있다.
앞서 제곱합(Sum of squares, SS)에 대해 설명할 때 제곱합을 이용하는 방법이 끝까지 살아남은 이유는 전체 제곱합은 특별한 의미를 지닌 제곱합들로 쪼개 생각할 수 있기 때문이라고 했다. 아래 꼭지에서 증명할 수 있듯이 $SS_\text{tot}$은 $SS_\text{bet}$와 $SS_\text{wit}$로 나눠 쓸 수 있다.
\[SS_{\text{tot}}=SS_{\text{bet}} + SS_{\text{wit}}\]그 뿐인가? 자유도(degree of freedom)도 마찬가지 구조로 쪼개 생각할 수 있다.
\[DF_{\text{tot}}=DF_{\text{bet}} + DF_{\text{wit}}\]
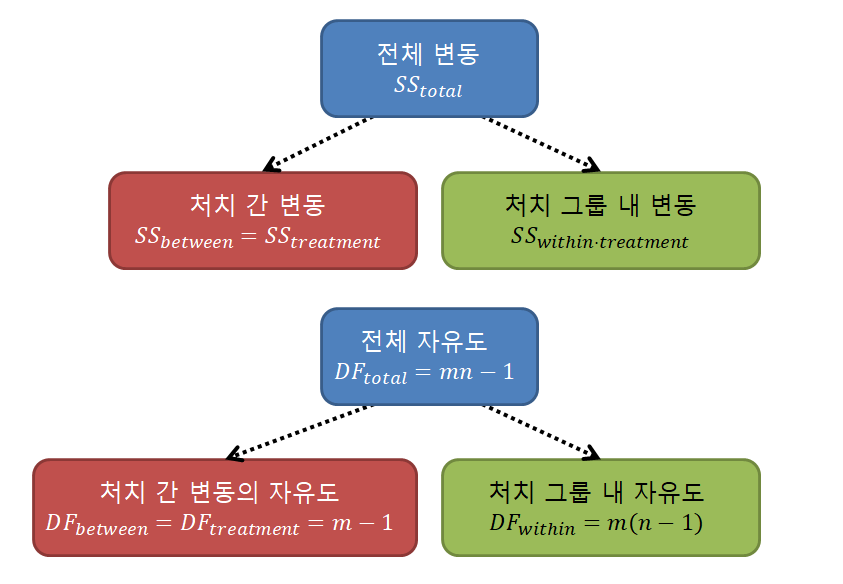
그림 2. one-way ANOVA에서 제곱합, 자유도의 분해(partitioning)
이 쯤 되면 ANOVA를 공부하는데 왜 제곱합(Sum of Squares, SS)이 필요한지 조금은 이해할 수 있을 것이다.
SS를 공부하는 것은 total SS를 특정한 의미를 갖는 SS로 분해할 수 있기 때문에 사용한다.
그리고, 그것이 말해주는 것은 특정한 그 의미 때문에 발생하는 변동에 관한 것이므로, 이 변동이 우리가 알 수 없는 error에 의해 발생하는 변동에 비해 얼마나 큰지를 체크할 수 있게 해준다.
거기에 F 값을 계산할 때는 제곱합을 그대로 사용해주는 것은 아니고 제곱합으로 표현된 변동을 자유도로 나눠주어서 샘플 수 혹은 그룹 수가 늘어나게 되어 발생할 수 있는 오류를 미연에 방지해준다.
이번에는 total SS를 between traetment SS와 within treatment SS로 나눌 수 있다는 것을 수식적으로 증명해보고, 그 다음에는 예제 문제를 풀어보도록 하자.
(skip 가능) ANOVA Sum of Squares의 분할 (증명)
※ $SS_\text{tot}=SS_\text{bet} + SS_\text{wit}$의 증명과정은 필수적인 것은 아닙니다. 너무 복잡하다고 생각되시면 skip하세요.
$SS_\text{tot}=SS_\text{bet} + SS_\text{wit}$임을 확인하기 위해 $SS_\text{tot}$의 괄호 안에 있는 식을 아래와 같이 분할해 생각해보자.
\[(X_{ts}-\bar{X}) = (\bar{X}_t - \bar{X}) + (X_{ts}-\bar{X}_t)\]여기서 양변을 제곱하면,
\[(X_{ts}-\bar{X})^2 = (\bar{X}_t - \bar{X})^2 + (X_{ts}-\bar{X}_t)^2 + 2(\bar{X}_t-\bar{X})(X_{ts}-\bar{X}_t)\]과 같다.
여기서 모든 샘플에 대한 합을 구하면 total SS를 구하는 것과 같다는 점을 알 수 있다.
\[SS_\text{tot} = \sum_t\sum_s(X_{ts}-\bar{X})^2\] \[=\sum_t\sum_s(\bar{X}_t - \bar{X})^2 + \sum_t\sum_s(X_{ts}-\bar{X}_t)^2 + \sum_t\sum_s2(\bar{X}_t-\bar{X})(X_{ts}-\bar{X}_t)\]위 식에서 첫 번째 항의 괄호 내부 식은 $s$와 관계없는 식이므로,
\[\sum_t\sum_s(\bar{X}_t-\bar{X})^2=n\sum_t(\bar{X}_t-\bar{X})^2\]이며 이것은 $SS_\text{bet}$와 같다.
한편, 세 번째 항은 다음과 같이 쓸 수 있는데,
\[\sum_t\sum_s2(\bar{X}_t-\bar{X})(X_{ts}-\bar{X}_t) =2\sum_t\left( (\bar{X}_t-\bar{X})\sum_s(X_{ts}-\bar{X}_t) \right)\]여기서 가장 내부의 $\sum_s$에 관한 식을 보면,
\[\sum_s(X_{ts}-\bar{X}_t)=\sum_sX_{ts}-\sum_s\bar{X}_t\] \[=\sum_sX_{ts}-n\bar{X}_t\]과 같이 풀어 쓸 수 있는데, $\bar{X}_t$는 정의상
\[\bar{X}_t=\frac{1}{n}\sum_sX_{ts}\]이므로,
\[\Rightarrow \sum_s(X_{ts}-\bar{X}_t)=\sum_sX_{ts}-n\frac{1}{n}\sum_sX_{ts} = 0\]이다.
그러므로
\[SS_\text{tot} = \sum_t\sum_s(X_{ts}-\bar{X})^2\] \[=\sum_t\sum_s(\bar{X}_t - \bar{X})^2 + \sum_t\sum_s(X_{ts}-\bar{X}_t)^2 + \sum_t\sum_s2(\bar{X}_t-\bar{X})(X_{ts}-\bar{X}_t)\] \[=n\sum_t(\bar{X}_t - \bar{X})^2 + \sum_t\sum_s(X_{ts}-\bar{X}_t)^2 + 0\] \[=SS_\text{bet}+SS_\text{wit}\]이다.
One-Way ANOVA 예시 문제
아래와 같은 데이터가 주어져 있다고 생각해보자.
이 때, 네 그룹 중 한 그룹이라도 다른 모집단에서 추출되었을 가능성이 있는지 타진해보도록 하자.
각 그룹의 샘플들은 모두 독립적으로 추출되었다고 생각하면 One-Way ANOVA를 이용해볼 수 있다.
| 그룹 1 | 그룹 2 | 그룹 3 | 그룹 4 |
|---|---|---|---|
| 4.6 | 4.6 | 4.3 | 4.3 |
| 4.7 | 5.0 | 4.4 | 4.4 |
| 4.7 | 5.2 | 4.9 | 4.5 |
| 4.9 | 5.2 | 4.9 | 4.9 |
| 5.1 | 5.5 | 5.1 | 4.9 |
| 5.3 | 5.5 | 5.3 | 5.0 |
| 5.4 | 5.6 | 5.6 | 5.6 |
앞서 공부한 방식을 그대로 이용하기 위해 그룹 내 분산과 그룹 간 분산을 Sum of Squares를 이용해 계산하자.
먼저 그룹 내 분산 $s^2_\text{wit}$을 계산해보자.
각 그룹별로 평균을 내고, 평균에서 얼마만큼 떨어져있는지를 계산하자.
각 그룹별로 평균은
\[\bar{X}_1 = 4.9571, \bar{X}_2 = 5.2286, \bar{X}_3 = 4.9286, \bar{X}_4 = 4.8000\]과 같다.
그러므로 각 그룹 별 그룹 내 sum of squares인 $SS_1, SS_2, SS_3, SS_4$를 구하면,
\[SS_1 = (4.6-\bar{X}_1)^2 + (4.7 - \bar{X}_1) ^2 + (4.7 - \bar{X}_1) ^2 + \cdots + (5.4-\bar{X}_1)^2 = 0.5971\] \[SS_2 = (4.6-\bar{X}_2)^2 + (5.0 - \bar{X}_2) ^2 + (5.2 - \bar{X}_2) ^2 + \cdots + (5.6-\bar{X}_2)^2 = 0.7343\] \[SS_3 = (4.3-\bar{X}_3)^2 + (4.4 - \bar{X}_3) ^2 + (4.9 - \bar{X}_3) ^2 + \cdots + (5.6-\bar{X}_3)^2 = 1.2943\] \[SS_4 = (4.3-\bar{X}_4)^2 + (4.4 - \bar{X}_4) ^2 + (4.5 - \bar{X}_4) ^2 + \cdots + (5.6-\bar{X}_4)^2 = 1.2000\]이므로 $SS_\text{wit}$는
\[SS_\text{wit}=\sum_t SS_t = 0.5971+0.7343+1.2943+1.2000 = 3.8257\]이고 $DF_\text{wit}$는
\[DF_\text{wit} = m(n-1) = 4\times(7-1) = 24\]이므로 $MS_\text{wit}$는
\[MS_\text{wit} = \frac{SS_\text{wit}}{DF_\text{wit}}=\frac{3.8257}{24}=0.1594\]이다.
이번에는 그룹 간 분산 $s^2_\text{bet}$을 계산해보자.
각 그룹 별 평균은 앞서 확인했기 때문에 이 그룹 별 평균들이 전체 평균(grand mean)으로부터 얼마나 떨어져있는지를 파악함으로써 그룹 간 분산을 구할 수 있다.
전체 평균은
\[\bar{X}= 4.9786\]이므로,
\[SS_\text{bet}=n \sum_{t}(\bar{X}_t-\bar{X})^2\] \[= 7\times \left((4.9571-4.9786)^2+(5.2286-4.9786)^2 +(4.9286-4.9786)^2 + (4.8000-4.9786)^2\right)\notag\] \[=0.6814\]이고,
\[DF_\text{bet}=m-1 = 3\]이므로,
\[MS_\text{bet}=\frac{SS_\text{bet}}{DF_\text{bet}}=0.2271\]임을 알 수 있다.
따라서, 우리가 구하고자 하는 F 값은
\[F = \frac{MS_\text{bet}}{MS_\text{wit}}=\frac{0.2271}{0.1594}=1.4249\]임을 알 수 있으며, 분자, 분모의 자유도는 각각 3, 24이므로 이 때 대응되는 우리의 $F$값의 p-value는 0.26에 불과하다.
One-way ANOVA의 결과를 정리하면 다음과 같다.
| Source | SS | df | MS | F | Prob > F |
|---|---|---|---|---|---|
| Between | 0.68143 | 3 | 0.22714 | 1.42 | 0.26 |
| Within | 3.82571 | 24 | 0.1594 | ||
| Total | 4.50714 | 27 |
One-Way RM ANOVA
Motivation 파트에서 설명했듯이 Repeated Measures ANOVA(이후 RM ANOVA)는 피험자 한 명이 여러 번의 treatment를 받은 경우에 적용할 수 있는 분석 기법이다.
One-Way ANOVA에서는 전체 제곱합(Sum of Squares 이하 SS)이 그룹 간 변동($SS_\text{bet}$)과 그룹 내 변동($SS_\text{wit}$)으로 나눠졌다고 하면
RM ANOVA에서는 전체 제곱합이 피험자 간 변동(between subject SS)과 피험자 내 변동(within subject SS)로 나뉘며, 피험자 내 변동이 treatment에 의해 생기는 변동과 그 외 잔여 변동으로 한 번 더 나뉘게 된다.
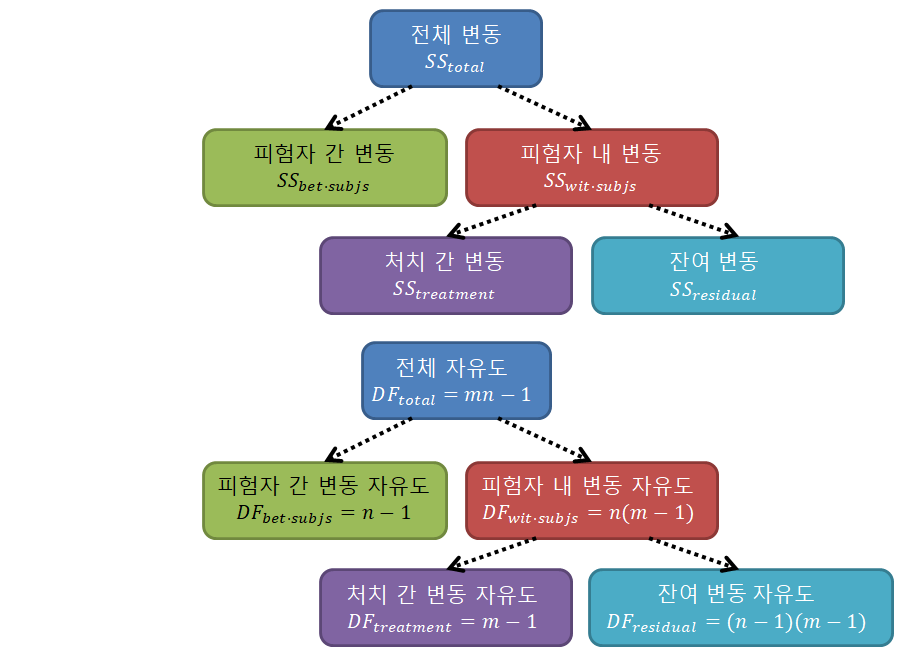
그림 3. 반복측정 분산 분석에서 변동 및 자유도의 분해(partitioning)
선뜻 보기에는 변동이 더 복잡하게 많이 나눠지니까 이해하기 어려울 수도 있겠다 생각이 들지만, 가장 중요하게 다루어야 하는 문제는 우리가 어떤 변동에 관심이 있는지를 정확히 캐치하는 것이다.
만약 100명의 헬스장 회원들이 3회에 걸쳐 체지방을 측정한다고 했을 때, 우리는 어떤 변동에 집중해야 할까?
회원들 간의 변동량(between subjects variation), 회차에 따른 체지방 측정량의 변화(between treatments variation), 잔여 변동(residual variation) 세 가지를 놓고 생각해보자.
여기서 우리는 회차에 따른 체지방 측정량의 변화에 대해 관심이 있다.
그리고 이것을 통계적으로 처리하기 위해 마치 t-test를 공부할 때 그룹 간 차이를 불확실성으로 나누어주었듯이
시간에 따른 체지방 측정량의 변동값을 잔여 변동으로 나누어준 값을 가지고 어떤 결과를 내는 것이 우리의 관심사가 될 수 있다는 것을 알 수 있다. 잔여 변동이라는 말이 우리가 측정할 수 없는 error에 대한 변동이라는 말을 내포하고 있기 때문이다.
따라서 우리는 F-value를 계산할 때 시간에 따른 체지방 측정량의 변동값과 잔여 변동량을 나누어 계산해준 뒤 유의성을 판단하면 되는 것이다.
RM ANOVA의 계산 수행 과정
앞서 간략하게 소개한 RM ANOVA의 분석 과정을 구체적으로 계산해보면서 진행해보자.
우선은 RM ANOVA를 이용해 분석할 수 있는 반복측정 데이터의 구조를 살펴보자.
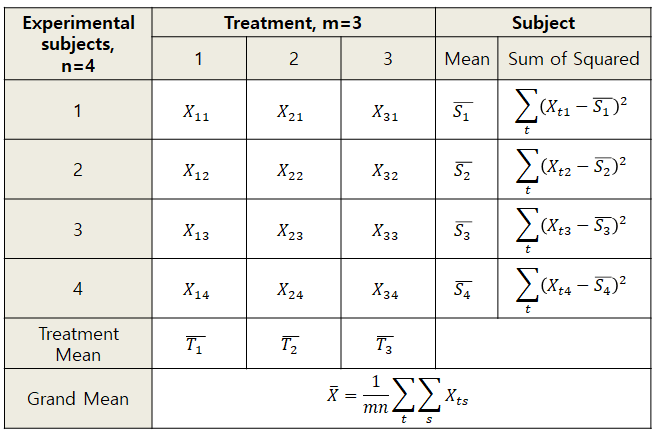
그림 4. 반복측정 데이터를 표와 기호로 정리한 것
그림 4에서는 반복측정 데이터를 표와 기호로 정리했다. 선뜻 보기에는 그림 1의 데이터와 다를게 없어보이지만 가장 핵심적인 차이는 그림 4에서 주어진 데이터들은 각 treatment 그룹에 있는 subject들이 같은 subject들이라는 것이다. 가령 그림 1에서는 데이터의 첫 번째 행에 있는 값들($X_{11}, X_{21}, X_{31}$)은 서로 다른 1번 피험자들이 수행하여 얻은 값이지만, 그림 4에서는 데이터 첫 번째 행에 있는 값들($X_{11}, X_{21}, X_{31}$)은 모두 동일한 피험자가 세 차례에 걸쳐 획득한 데이터가 되는 것이다.
그리고 그림 4에서는 Subject mean이라는 값도 존재한다. $\bar{S}_1, \bar{S}_2, \cdots$ 등으로 쓰인 값이며 각각은 다음과 같이 계산된다.
\[\bar{S}_s=\frac{\sum_t X_{ts}}{m}\]비슷한 방식으로 treatment mean 값이 있다. $\bar{T}_1, \bar{T}_2, \cdots$ 등으로 쓰인 값이며 각각은 다음과 같이 계산된다.
\[\bar{T}_t=\frac{\sum_s X_{ts}}{n}\]또, 전체 평균(grand mean) 값이 있으며,
\[\bar{X}=\frac{\sum_t\sum_s X_{ts}}{mn}\]이로부터 total SS를 계산할 수 있다.
\[SS_\text{tot}=\sum_t\sum_s\left(X_{ts}-\bar{X}\right)^2\]total SS에 대응되는 자유도는 $mn-1$이다.
이제 One-Way ANOVA를 공부할 때 total SS를 그룹 간 SS와 그룹 내 SS로 분할할 수 있었던 것 처럼 RM ANOVA에서도 total SS를 분할해보자.
RM ANOVA에서는 total SS를 크게 within subject SS와 between subjects SS로 나눌 수 있다.
먼저 within subject SS에 대해 알아보자. within subject SS는 말 그대로 각 피험자들이 받은 treatment에 대한 반응값이 각각의 피험자들의 평균값에서 얼마나 떨어졌는지에 관한 값이다.
가령, 1번 피험자의 within subject SS는 아래와 같이 계산할 수 있다.
\[SS_\text{wit subj 1} = \sum_t(X_{t1}-\bar{S}_1)^2\]2번 피험자의 경우에도 비슷한 방법으로 아래와 같이 within subject SS를 계산할 수 있을 것이다.
\[SS_\text{wit subj 2} = \sum_t(X_{t2}-\bar{S}_2)^2\]따라서, 모든 피험자들에 대한 within subject SS는 다음과 같다.
\[SS_\text{wit subjs} = SS_\text{wit subj 1}+SS_\text{wit subj 2}+SS_\text{wit subj 3}+SS_\text{wit subj 4}\] \[=\sum_t\sum_s(X_{ts}-\bar{S}_s)^2\]within subject SS의 자유도는 각각의 피험자가 갖는 자유도가 $m-1$이므로 $n$명의 피험자에 대해서는 $n(m-1)$이 된다.
다음으로 between subjects SS를 계산해보자. between subjects SS는 각 피험자들의 평균값들이 grand mean으로부터 얼마나 떨어져있는지를 계산하는 값이므로 다음과 같이 계산할 수 있게 된다.
\[SS_\text{bet subjs} = m \sum_t(\bar{S}_s-\bar{X})^2\]여기서 앞에 m이 곱해지는 것은 각 피험자들의 평균값은 m 개의 처치에 대한 평균적 반응이기 때문에 곱해지는 것이라고 볼 수 있다.
(이런 방식으로 생각하는 것은 one-way ANOVA에서 between group SS를 계산할 때 그룹 개수를 곱해주는 것과 같은 이치이다.)
피험자수가 n이므로 between subjects SS의 자유도는 $n-1$이 된다.
일단 여기까지 계산해보면 total SS를 다음과 같이 분할할 수 있는데 필요한 두 개의 SS 값들을 얻은 것이다.
\[SS_\text{tot} = SS_\text{bet subjs} + SS_\text{wit subjs}\]이제 마지막으로 within subject SS를 treatment에 의한 SS와 나머지(residual) SS로 분할해보자.
treatment에 의한 SS는 각각의 treatment 평균들이 grand mean으로부터 떨어진 정도를 이용하면 되기 때문에,
\[SS_\text{treat} = n \sum_t(\bar{T}_t -\bar{X})^2\]라고 쓸 수 있다. $n$이 앞에 곱해지는 것은 between subjects SS를 구할 때와 마찬가지 이유로 $\bar{T}_t$는 어찌되었건 평균값이기 때문에 평균의 표준 오차를 이용해 분산을 구해주는 과정을 이용하는 것이기 때문에 $n$이 붙는 것이다.
treatment에 의한 SS의 자유도는 $m-1$이 된다.
언급한대로 within subject SS는 다음과 같이 쪼개서 쓸 수 있게 된다.
\[SS_\text{wit subjs} = SS_\text{treat} + SS_\text{res}\]그러므로 우리가 직접 계산할 수 없는 $SS_\text{res}$는 다음과 같이 얻을 수 있으며,
\[SS_\text{res}=SS_\text{wit subjs} - SS_\text{treat}\]residual의 자유도 역시 다음과 같이 계산할 수 있다.
\[DF_\text{res} = DF_\text{wit subjs} - DF_\text{treat} = n(m-1) - (m-1) = (n-1)(m-1)\]이로써 최종적으로 우리가 궁금해하는 treatment의 변동에 의해 계산되는 F 값을 계산해보면 다음과 같다.
\[F = \frac{SS_\text{treat}/DF_\text{treat}} {SS_\text{res}/DF_\text{res}}=\frac{MS_\text{treat}}{MS_\text{res}}\]다시 말해 이 F 값을 이용하면 여러 회에 걸쳐 측정한 처치가 모든 시점에서 통계적으로 유의한 차이가 없다는 귀무가설을 검증할 수 있게 되는 것이다.
용어 상의 주의점
RM ANOVA를 공부할 때 어려운 점 중 하나는 One-way ANOVA를 공부할 때 생긴 between variance, within variance라는 용어 때문이다.
RM ANOVA를 수행해주게 되면 모든 Sum of Squares를 해석하는 관점은 treatment에 관한 것이 아니고 subject에 관한 것으로 바뀐다.
아래의 그림을 보자.
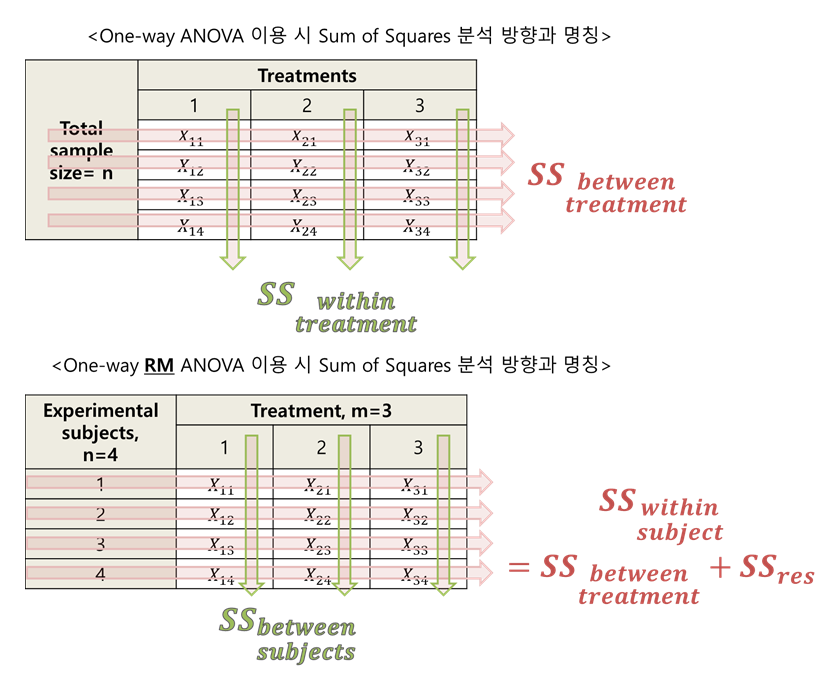
그림 5. One-way ANOVA 와 RM ANOVA를 이용할 때의 데이터 구조 및 SS 계산
One-way ANOVA를 공부할 때 막연히 between variance라고 했던 것의 방향은 그림 5의 윗쪽 테이블에서 좌우방향이다. 그런데, 그림 5의 아랫쪽 테이블을 보자. 좌우방향으로 계산해주는 sum of squares는 within subject SS가 된다.
생각해보면 아랫쪽 테이블에선 각 행들이 한 명 한 명의 피험자들을 뜻하기 때문에 within subject에 관한 Sum of Squares를 계산한다는 것을 알 수 있지만, within subject라는 말을 딱 보았을 때 within treatment에 관한 것으로 착각하지는 않았는가?
One-way ANOVA를 공부할 때 막연히 within, between 이렇게만 용어를 외워왔다면 이 부분에서 RM ANOVA를 공부할 때 헷갈리는 점이 분명 있었을 것이라 생각하여 노파심에 주의를 주고자 한다.
구형성
※ 구형성에 대한 자세한 내용은 Laerd Statistics의 글을 참고하여 작성한 것입니다. 더 자세한 내용은 해당 글을 읽는 것을 추천드립니다.
통계 프로그램을 이용해 RM ANOVA 분석을 수행하면 구형성 검정이라는 것을 수행해준다.
구형성을 가정한다고 하는 것은 모든 treatment 차이들을 조합(combination)해서 보았을 때 모든 조합 간의 차이 분산이 동일한 경우를 말한다.
차이의 분산값을 굳이 보려는 이유는 사후 분석 시 시점 조합 간 paired t-test를 수행해주게 될 것이고 이 때 t-value의 분모에 차이의 분산을 이용한 표준오차가 이용되기 때문이다.
아래의 그림을 보면서 얘기를 계속 이어나가 보자.
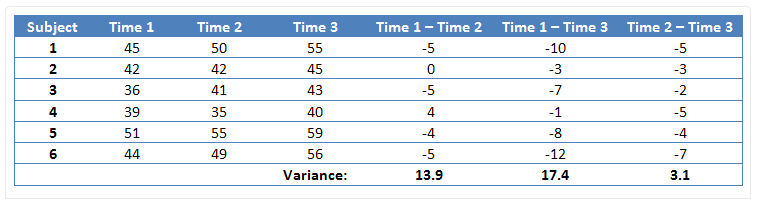
그림 6. 구형성이 만족되지 못하는 경우의 데이터
출처: sphericity, Laerd statistics
위 그림 6의 경우에는 세 번 반복측정한 데이터에 대해 확인하였으며, (Time 1 - Time 2), (Time 1 - Time 3), (Time 2 - Time 3)의 차이를 계산하고 이 차이값들의 분산을 확인 및 비교해 본 것이다.
육안으로 보기에도 세 개의 분산(13.9, 17.4, 3.1) 중 세 번째 분산 값이 확연히 작은 것을 볼 수 있다. 이런 경우에 우리는 구형성 가정이 위배되었다(violated)고 말한다.
구형성 가정이 위배 되게 되면 1종 오류가 증가할 수 있다. 즉, 실제로는 차이가 없는데 차이가 있다고 결과를 잘못 내게 될 가능성이 커진다는 것이다. 그 이유는 시점 간 차이를 확인할 때 불공평한 비교가 수행되기 때문이다.
이에 대해 그림 6의 경우를 가지고 계속 설명해보자면, Time 1과 Time 2를 비교할 때 보다 Time 2와 Time 3을 비교할 때 더 쉽게 유의한 차이를 볼 수 있게 될 것이다.
그런데 그 이유가 Time 2와 Time 3의 그룹 평균의 차이가 컸기 때문이 아니라 Time 2와 Time 3 간의 차이의 분산이 작기 때문에 유의한 차이를 보게 될 것이라는 것이다.
즉, paired t-test를 수행하게 될 때 t-value의 분모에는 표준 오차가 들어가고, 이 표준 오차는 차이의 분산에 비례하는 값이기 때문이다.
그래서 RM ANOVA 분석 시에 구형성이 가정이 위배되면 1종 오류는 증가한다. 실제로는 시점 간 평균 차이가 없는데, 특정 시점 간 비교 시에는 차이의 분산이 작아서 (paired) t-value가 커 보일 수 있다.
Mauchly’s test (모클리 테스트)
Mauchly’s test는 구형성을 검정해주는 테스트이다. SPSS나 기타 통계 프로그램을 이용해서 RM ANOVA를 테스트하면 Mauchly’s test 결과를 보여주게 되어 있다.
이 때, Mauchly’s W는 1에 가까울 수록 데이터가 구형성 가정을 만족하는 것임을 말해준다.
또, Mauchly’s test의 귀무가설은 구형성 가정을 만족한다는 것이기 때문에 결과물 중 p-value가 0.05보다 크다면 구형성을 만족하는 것이고, p-value가 0.05보다 작으면 구형성을 만족하지 못한다고 해석할 수 있는 것이다.
Epsilon 보정
RM ANOVA을 이용시 데이터가 구형성을 만족하지 못한다면 자유도를 보정해줌으로써 분석을 진행한다.
즉, Mauchly’s test에서 p-value가 0.05보다 작아서 구형성을 만족하지 못한다고 판단하는 경우 RM ANOVA의 결과에서 자유도를 수정해주면 되는 것이다.
이 때 자유도를 수정하기 위해 곱해주는 상수값이 epsilon이다. epsilon의 종류는 크게 Greenhouse-Geisser (G-G)의 epsilon과 Huyhn-Feldt (H-F)의 epsilon 두 가지가 있다.
epsilon 값은 1보다 작거나 같은 값인데, 그러다보니 구형성을 만족하지 못하면 자유도를 떨어뜨리는 방식으로 보정이 진행된다는 것을 알 수 있다.
생각해보면 일리 있는 방식인 것이, 구형성을 만족하지 못하면 앞서 언급한대로 1종 오류가 증가하므로 자유도를 떨어뜨려 같은 F 값이더라도 쉽게 유의성을 만족하지 못하게 만들어 버리는 것이다.
이로써 높아진 1종 오류율을 만회할 수 있게 하는 것이다.
G-G epsilon과 H-F epsilon 중 어떤 값을 사용해야 할지 고민이 된다면 아래의 flow chart를 참고해보자.

그림 7. 그림 6에서 제시된 데이터의 측정 시간 별 boxplot 도시
관례적으로 Mauchly’s test에서 구형성 가정이 위배된다고 했을 때 G-G의 epsilon 값이 0.75보다 작으면 G-G epsilon을 사용해 자유도를 수정해준다.
반면, Mauchly’s test에서 구형성 가정이 위배되었는데, G-G의 epsilon 값이 0.75보다 크면 H-F의 epsilon 값을 사용해 자유도를 수정한다.
RM ANOVA 예시 문제
우리는 그림 6에서 사용되었던 데이터를 그대로 이용해 RM ANOVA를 수행해보도록 하자.
우선 그림 6에서 주어진 데이터를 측정 시점 별로 boxplot을 이용해 그려주면 다음과 같은 것을 알 수 있다.
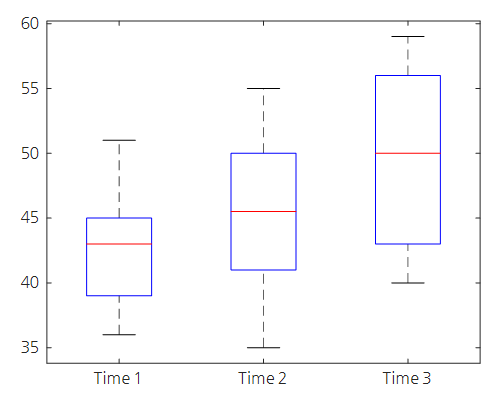
그림 8. 그림 6에서 제시된 데이터의 측정 시간 별 boxplot 도시
눈으로 보기에도 각 시점별로 데이터 값이 평균적으로 상승한다는 것을 짐작할 수 있다.
우리는 세 개의 Sum of Squares를 계산해야 하는데, 각각은 between subject SS, within subject SS treatment SS 이다.
이를 계산하기 위해 grand mean $\bar{X}$와 측정 시점 그룹 별 평균, 피험자 평균값을 계산해보면 다음과 같다2.
\[\bar{X} = 45.94\] \[\bar{T}=\begin{bmatrix}42.83 & 45.33 & 49.66\end{bmatrix}\] \[\bar{S} = \begin{bmatrix}50.00\\43.00\\40.00\\38.00\\55.00\\49.66\end{bmatrix}\]여기서 데이터를 보면 피험자 수 $n=6$이고, 시점의 수 $m=3$임을 알 수 있다.
세 가지 SS 중 between subject SS를 먼저 구해보면 다음과 같다.
\[SS_\text{bet subj}= m \sum_t(\bar{S}_s-\bar{X})^2 = 658.2778\]그리고 within subject SS는
\[SS_\text{wit subj} = \sum_t\sum_s(X_{ts}-\bar{S}_s)^2 = 200.6667\]마지막으로 treatment SS는
\[SS_\text{treat}=n \sum_t(\bar{T}_t -\bar{X})^2 = 143.4444\]와 같다.
그리고 within subject SS와 treatment SS의 차이를 이용해 residual SS를 구할 수 있으므로,
\[SS_\text{res}=SS_\text{wit subj} - SS_\text{treat} = 57.2222\]와 같이 계산된다.
한편, between subject, within subject, treatment, residual에 대한 DF는 각각 다음과 같다.
\[DF_\text{bet subj}=n-1 = 5\] \[DF_\text{wit subj}=n(m-1) = 12\] \[DF_\text{treat}=m-1 = 2\] \[DF_\text{res} = (n-1)(m-1) = 10\]최종적으로 관심사인 $F$ 값은 다음과 같이 계산될 수 있다.
\[F=\frac{SS_\text{treat}/DF_\text{treat}}{SS_\text{res}/DF_\text{res}}=\frac{MS_\text{treat}}{MS_\text{res}} = 12.5340\]자유도가 (2, 10)인 경우의 p-value = 0.95에 해당하는 F 값은
\[F_{p=0.95}(2,10)=4.1028\]인데, 우리에게 주어진 $F$ 값은 12.5340으로 4.1028보다 크므르 우리의 데이터는 최소한 한 시점에서는 유의한 차이를 보이는 것이라고 결론지을 수 있다.
Jamovi
Repeated Measures ANOVA를 수행해줄 수 있는 소프트웨어는 많이 있으나 GUI 기반으로 되어 있는 소프트웨어를 꼽자면 Jamovi를 추천하고 싶다.
다른 이유는 없고 무료로 쓸 수 있기 때문이다. SPSS나 Python 등에서도 RM ANOVA는 모두 수행이 가능하다.
Jamovi에서는 아래와 같이 그림 6의 데이터를 입력해주고 RM ANOVA를 수행하면 된다.
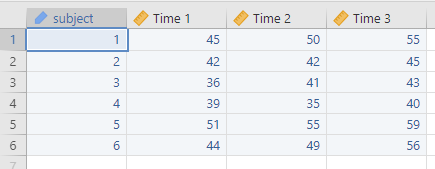
그림 9. Jamovi를 이용해 얻은 그림 6의 데이터를 입력한 것
RM ANOVA 분석 결과를 보면 앞서 손으로 계산한 RM ANOVA의 F 값과 같은 결과를 얻은 것을 알 수 있다.
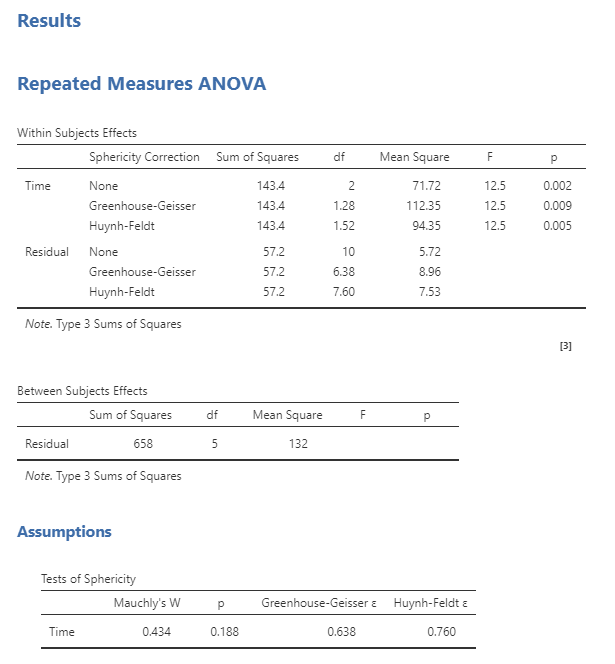
그림 10. Jamovi를 이용해 얻은 RM ANOVA 분석 결과
다만, 추가적으로 구형성에 대한 Mauchly’s test 결과물과 G-G epsilon 혹은 H-F epsilon 값이 적용된 경우에 대해서도 다루어주고 있다.
구형성에 대한 테스트 및 epsilon 값은 손으로 계산하기가 워낙에 어렵기 때문에 통계 소프트웨어를 활용하는 것을 더 추천한다.
참고문헌
- Primer of biostatistics, 7th ed., S. Glantz / Ch. 9 Experiments when each subject receives more than one treatment
- sphericity, Leard statistics
아래는 Jamovi 프로그램에 관련된 참고문헌 리스트입니다.
- The jamovi project (2021). jamovi. (Version 1.6) [Computer Software]. Retrieved from https://www.jamovi.org.
- R Core Team (2020). R: A Language and environment for statistical computing. (Version 4.0) [Computer software]. Retrieved from https://cran.r-project.org. (R packages retrieved from MRAN snapshot 2020-08-24).
- Singmann, H. (2018). afex: Analysis of Factorial Experiments. [R package]. Retrieved from https://cran.r-project.org/package=afex.