Prerequisites
이 포스팅을 더 잘 이해하기 위해서는 아래의 내용에 대해 알고 오시는 것이 좋습니다.
푸리에 변환의 아이디어
푸리에 변환의 아이디어는 단순하다. $T$ 를 주기로 하는 주기함수 $x(t)$ 에 대해서, $T$ 를 무한정 크게 늘린다면, 그것은 사실은 비주기 함수와 같다고 할 수 있는 것이다.
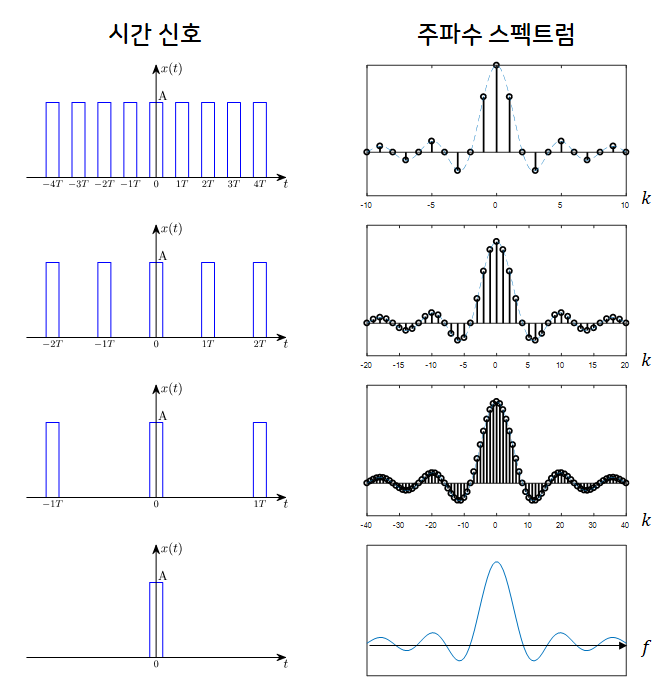
그림 1. 주기 함수의 주기를 무한정 크게 하면 어떤 일이 일어날까?
위 그림을 보면 사각 펄스의 주기를 계속 늘리게 되었을 때 주파수 스펙트럼이 변화하는 것을 볼 수 있다. 특별히 스펙트럼의 표현 간격이 주기가 늘어남에 따라 계속해서 좁아지는 것을 볼 수 있다.
주기가 무한정 커지게 되면 표현 간격은 무한소로 작아지게 되어 주파수 스펙트럼이 연속 신호로 바뀌게 된다.
푸리에 변환는 어떠한 비주기함수도 sinusoidal function을 이용해서 decompose할 수 있다는 것을 의미하기 때문에 큰 의의를 가진다.
이번 post에서는 푸리에 변환의 유도과정에 대해 알아보고자 한다.
푸리에 변환의 유도과정
주기가 $T$ 인 주기함수 $x(t)$는 다음과 같이 나타낼 수 있다.
\[x(t) = \sum_{k=-\infty}^{\infty}{c_k \exp\left(j \frac{2\pi k}{T}t\right)}\]푸리에 급수에서 푸리에 변환으로 넘어가는 과정에서 필요한 것은 $T\rightarrow\infty$ 이다.
식 (2)는 $x(t)$가 주기함수이기 때문에 다음이 성립한다.
\[c_k = \frac{1}{T}\int_{0}^{T}{x(t) \exp\left(-j \frac{2\pi k}{T}t\right)dt} = \frac{1}{T}\int_{-T/2}^{T/2}{x(t) \exp \left(-j \frac{2\pi k}{T}t\right)dt}\]식 (1)에 식 (3)을 대입한 다음 $T$ 를 무한하게 크게 만들면,
\[\lim_{T\rightarrow \infty}x(t) = \lim_{T\rightarrow\infty} \sum_{k=-\infty}^{\infty}\left[ \frac{1}{T}\int_{-T/2}^{T/2}{x(t) \exp\left(-j \frac{2\pi k}{T}t\right)dt} \right] exp\left(j\frac{2\pi k}{T}t\right)\]식 (4)를 약간 변형해 $1/T$ 를 우항의 가장 오른쪽으로 이동시켜보자.
\[\lim_{T\rightarrow \infty}x(t) = \lim_{T\rightarrow\infty} \sum_{k=-\infty}^{\infty}\left[ \int_{-T/2}^{T/2}{x(t) \exp\left(-j \frac{2\pi k}{T}t\right)dt} \right] exp\left(j\frac{2\pi k}{T}t\right)\frac{1}{T}\]여기서 정적분의 정의를 이용해 식 (5)에서 몇 가지 기호들이 다음처럼 바뀔 수 있음을 염두해두자.
- $1/T \rightarrow df$
- $k/T \rightarrow f$ 1
- $T/2 \rightarrow \infty$
- $-T/2 \rightarrow -\infty$
계산 상의 편의를 위해 식 (5)의 대괄호 ‘[ ]’ 내부에 있는 식을 먼저 계산하자.
\[\lim_{T\rightarrow\infty}\int_{-T/2}^{T/2}x(t) \exp\left(-j\frac{2\pi k}{T}t\right)dt = \int_{-\infty}^{\infty}x(t) \exp\left(-j2\pi f t\right)dt\]식 (6)의 결과는 신호 $x(t)$ 를 푸리에 변환한 결과로 볼 수 있다.
즉,
\[X(f) = \int_{-\infty}^{\infty}x(t) \exp\left(-j2\pi ft \right)dt\]이다.
한편, 식 (5)에 식 (7)의 결과를 대입시켜 다음과 같이 쓸 수 있다.
\[\sum_{k=-\infty}^{\infty}\lim_{T\rightarrow\infty}X(f) \exp\left(j\frac{2\pi k}{T}t\right)\frac{1}{T}\]이제, 정적분의 정의에 의해서 식 (8)은 다음과 같이 쓸 수 있다.
\[\sum_{k=-\infty}^{\infty}\lim_{T\rightarrow\infty}X(f) \exp\left(j\frac{2\pi k}{T}t\right)\frac{1}{T} =\int_{-\infty}^{\infty}X(f) \exp\left(j2\pi f t\right)df\]위의 과정을 통해 어떠한 연속시간 함수 $x(t)$ 를 다음과 같이 푸리에 변환할 수 있음을 유도하였다.
\[x(t) = \int_{-\infty}^{\infty}X(f) \exp\left(j2\pi f t\right)df\] \[X(f) = \int_{-\infty}^{\infty}x(t) \exp\left(-j2\pi ft\right)dt\]추가로 푸리에 변환는 수렴조건이 필요하다. 복소 지수함수 $exp(-j2\pi ft)$ 의 크기는 1 이므로 수렴 조건은 다음과 같다.
\[X(f) = \int_{-\infty}^{\infty}x(t) \exp\left(-j2\pi f t \right)dt \leq \int_{-\infty}^{\infty} x(t) dt \leq \int_{-\infty}^{\infty}|x(t)| dt < \infty\]이외에도 어떤 유한한 시간 구간에서 신호의 극대, 극소점의 수가 유한해야 하며, 어떤 유한한 시간 구간에서 신호의 불연속점의 수가 유한해야 한다는 조건이 필요하다.
푸리에 변환의 성질
푸리에 변환은 몇 가지 주요한 성질이 있다.
선형성
푸리에 변환은 다음을 만족하는 선형 변환이다.
임의의 신호 $x_1(t)$와 $x_2(t)$에 대해
\[ax_1(t) + bx_2(t) \Longleftrightarrow a X_1(f) + b X_2(f)\]쌍대성
푸리에 변환의 식을 자세히 살펴보면 $x(t)$와 $X(f)$의 공식이 거의 유사한 것을 볼 수 있다.
\[X(f) = \int_{-\infty}^{\infty}x(t)\exp\left(-j2\pi ft\right)dt\] \[x(t) = \int_{-\infty}^{\infty}X(f)\exp\left(j2\pi ft\right)df\]차이가 있는 것은 지수함수의 지수의 부호라는 것을 쉽게 알 수 있으며 $x(t)\leftrightarrow X(f)$이면 다음이 성립한다.
\[X(t) \Longleftrightarrow x(-f)\]이를 쌍대성(duality)라고 한다. 쌍대성을 이용해서 생각해내기 어려운 푸리에 변환을 쉽게 얻어낼 수 있다.
가령 사각 펄스의 푸리에 변환이 sinc 함수라는 사실을 알고 있기 때문에, sinc 함수의 푸리에 변환이 사각 펄스라는 사실을 추가적인 계산 없이도 유추해낼 수 있는 것이다.
시간 이동(time shift)
시간 영역에서 $t_0$만큼 이동하면 주파수 영역에서는 복소 지수 $\exp(-j2\pi ft_0)$를 곱한 것과 같다.
\[x(t-t_0)\Longleftrightarrow X(f)\exp(-j2\pi ft_0)\]이것은 시간 신호 전체에 대한 phase delay를 $t_0$만큼 걸어준 것과 같은 일을 하는 것이기 때문이다.
주파수 이동(frequency shift) 혹은 변조(modulation)
시간 영역에서 복소 지수 $\exp(j2\pi f_0 t)$를 곱해주는 것은 주파수 영역에서 $f_0$만큼 이동하는 효과를 나타냄.
\[\exp(j2\pi f_0 t)x(t) \Longleftrightarrow X(f-f_0)\]이를 조금만 응용해 생각해보면 원래 신호에 코사인, 사인 함수를 곱했을 때의 주파수 대역에서의 변화를 생각할 수 있다.
\[\cos(2\pi f_0 t)x(t) = \frac{1}{2}\left(\exp(j2\pi f_0 t) + \exp(-j2\pi f_0 t)\right)x(t)\]따라서,
\[\cos(2\pi f_0t) x(t)\Longleftrightarrow \frac{1}{2}\left(X(f-f_0) + X(f+f_0)\right)\]이고, 같은 방법으로
\[\sin(2\pi f_0t) x(t)\Longleftrightarrow \frac{1}{j2}\left(X(f-f_0) - X(f+f_0)\right)\]이다.
이러한 주파수 이동 혹은 변조는 AM 라디오에서 많이 쓰는 방법이다. AM 라디오는 원래의 소리 신호를 carrier 신호에 담아 전송한다.
carrier 신호는 소리 신호보다 더 높은 주파수를 갖는 신호인데, 먼 거리에 신호를 송출하기 위해서는 고주파 신호가 유리하기 때문에 이런식으로 Amplitude Modulation을 수행한다.
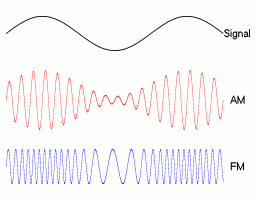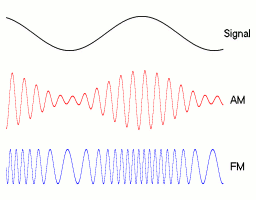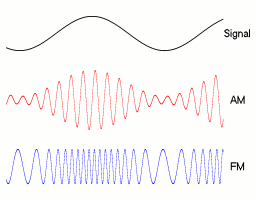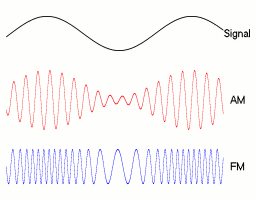
그림 2. AM, FM 변조
그리고 수신하는 라디오 입장에서는 캐리어 신호의 주파수를 이용해 다시 demodulation 해주면 원래의 음성 신호 (그림 2에서의 signal)를 복원할 수 있게 되는 것이다.
컨볼루션
시간 대역에서 컨볼루션이 주파수 대역에서 곱으로 표현되고, 주파수 대역에서 컨볼루션이 시간 대역에선 곱으로 표현된다.
\[x(t) * y(t) \Longleftrightarrow X(f)Y(f)\] \[x(t)y(t) \Longleftrightarrow X(f)*Y(f)\]컨볼루션 계산이 어려우나 각 신호의 푸리에 변환은 상대적으로 용이한 경우에 요긴하게 쓰일 수 있다.
-
시간의 역수의 값이 매우 작게 조금씩 커져간다. 이것은 $T\rightarrow\infty$ 일 때, $k$ 가 순서대로 하나씩 커져가기 때문인데, 결국 $k/T$ 는 연속적인 주파수의 영역을 이루게 된다는 것이다. ↩