Prerequisites

이번 포스팅의 내용을 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 기본 행렬

삼각행렬 소개

이번 LU 분해를 이해하기 위해선 아래의 삼각행렬이라는 용어를 조금 다루고 가는 것이 좋을 것 같아 짧게 소개한다.

선형대수학에서 종종 보이는 특이한 형태의 행렬 중 삼각행렬이라는 행렬이 있다. 이 행렬은 주대각선을 기준으로 대각 성분의 윗쪽이나 아랫쪽 항들의 값이 모두 0인 행렬을 말한다.

그래서 대각성분의 윗쪽 항들이 모두 0인 행렬을 하삼각행렬(lower triangular matrix)라고 하고, 대각 성분 아랫쪽 항들이 모두 0인 행렬을 상삼각행렬이라고 한다.

• 하삼각행렬(lower triangular matrix)

\[L=\begin{bmatrix} l_{1,1} & & & & 0 \\ l_{2,1} & l_{2,2} & & & \\ l_{3,1} & l_{3,2} & \ddots & & \\ \vdots & \vdots & \ddots & \ddots & \\ l_{n,1} & l_{n,2} & \cdots & l_{n,n-1} & l_{n,n} \end{bmatrix}\]

• 상삼각행렬(upper triangular matrix)

\[U=\begin{bmatrix} u_{1,1} & u_{1,2} & u_{1,3} & \cdots & u_{1,n} \\ & u_{2,2} & u_{2,3} & \cdots & u_{2,n} \\ & & \ddots & \ddots & \vdots \\ & & & \ddots & u_{n-1,n} \\ 0 & & & & u_{n,n} \end{bmatrix}\]

연립 방정식의 풀이 다시 생각해보기

연립 방정식의 풀이 과정에 들어가는 기본 행 연산들을 행렬로 표현해주기 위해 우리는 기본 행렬에 대해 생각해보았다.

잠깐 복습하면 기본행렬은 총 세 가지 종류가 있었는데 각각은

1. Row multiplication
2. Row switching
3. Row addition

이었다.

그리고 이런 기본 행 연산들을 통해서 해를 얻어주는 과정을 우리가 다시 잘 생각해보면 가장 아랫쪽에 있던 방정식에서는 가장 마지막 미지수에 대한 식만을 남기고, 그 위에 있는 방정식은 마지막 두 개의 미지수만을 남기는 식으로 미지수를 소거해 나가면 가장 아래에 있는 식으로부터 마지막 미지수에 대한 값을 얻고, 그 위에 있는 식에 대입하는 과정을 통해 그 다음 미지수에 대한 값을 얻고… 등의 순서로 미지수의 값들을 차례대로 얻어낼 수 있게 된다는 사실을 알 수 있다.

\[\begin{cases}x+y+z = 6 \\ 2x+3y-z=5 \\ 2x+3y+3z=17\end{cases} % 식 (3)\]

아래와 같은 연산을 수행하자.

\[r_2 \rightarrow r_2-2r_1 % 식 (4)\] \[r_3 \rightarrow r_3 - 2r_1 % 식 (5)\] \[\begin{cases}x+y+z = 6 \\ 0x+y-3z=-7 \\ 0x+y+z=5\end{cases} % 식 (6)\]

아래와 같은 연산을 수행하자.

\[r_3 \rightarrow r_3- r_2 % 식 (7)\] \[\begin{cases}x+y+z = 6 \\ 0x+y-3z=-7 \\ 0x+0y+4z=12\end{cases} % 식 (8)\]

그러면 아래에서부터 $4z=12$이므로 $z=3$임을 알 수 있고,

이 값을 두 번째 식에 대입해 $y=2$ 임을 알 수 있고,

$y=2, z=3$을 첫번째 식에 대입하면 $x=1$임을 알 수 있게 된다.

가장 마지막 미지수부터 처음 미지수로 계산해 나간다고 해서 이런 과정을 back substitution이라고 부른다.

Back substituion을 행렬로 표현해보자.

위에서 계산했던 해를 구하는 과정을 행렬로 표현해보면 어떨까?

즉, 식 (3) 방정식을 표현한 행렬

\[\left[\begin{array}{ccc|c} 1 & 1 & 1 & 6 \\ 2 & 3 & -1 & 5 \\ 2 & 3 & 3 & 17\end{array}\right]% 식 (9)\]

에 식 (4), (5), (7)과 같은 기본 행 연산들을 수행해줌으로써 식 (8)의 방정식을 표현한 행렬

\[\left[\begin{array}{ccc|c} 1 & 1 & 1 & 6 \\ 0 & 1 & -3 & -7 \\ 0 & 0 & 4 & 12\end{array}\right]\]

을 얻게 된 과정을 기본 행렬로 기본 행 연산들을 표현해 써보자는 것이다.

기본 행 연산들을 기본 행렬을 이용해 표현하면 다음과 같이 요약해서 쓸 수 있다.

\[\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 1\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ -2 & 0 & 1\end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix} \left[\begin{array}{ccc|c} 1 & 1 & 1 & 6 \\ 2 & 3 & -1 & 5 \\ 2 & 3 & 3 & 17\end{array}\right]= \left[\begin{array}{ccc|c} 1 & 1 & 1 & 6 \\ 0 & 1 & -3 & -7 \\ 0 & 0 & 4 & 12\end{array}\right]\]

원래의 $[A|b]$ 행렬 왼쪽에 붙은 기본 행렬들의 의미를 생각해본다면 다음과 같은 기본 행 연산들이다.

그림 1. 기본 행렬 연산을 통해서 얻게 된 최종 결과물로 back substitution을 수행할 수 있게 된다.

그러면 위에서 $x,y,z$에 대한 해를 구한 방법과 마찬가지로 결과로써의 우변의 행렬로부터 동일하게 $4z=12$라는 결과를 통해 $z=3$임을 알 수 있고, $y$와 $x$도 차례대로 알 수 있는 것이다.

그런데, 이 아이디어를 적용해서 조금 다른 시도를 생각해보자. 우리는 $[A|b]$ 대신에 방정식의 계수만 붙어있는 행렬 $A$에 대해서도 동일한 방법으로 기본 행렬을 곱해주면 우변의 행렬을 첨가(augment) 시키지 않은 꼴을 얻을 수 있다. 이 때, 얻게 되는 결과물은 앞서 소개한 상삼각행렬(upper triangular matrix)의 꼴일 것이다.

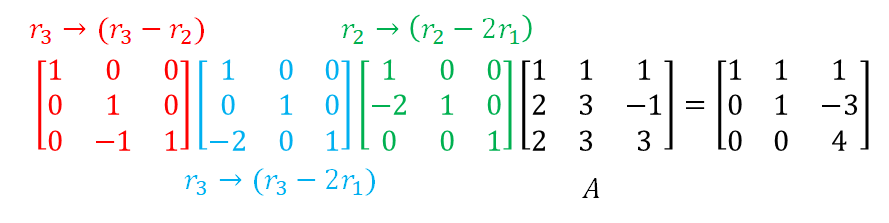
그림 2. 기본 행렬 연산을 통해서 계수 행렬 $A$를 상삼각행렬의 꼴로 바꿀 수 있다.

기본 행렬의 역행렬을 곱하기: LU 분해

그리고 기본 행렬 시간에 배웠던 것 처럼 기본 행렬들의 역행렬은 아주 간단한 형태를 띄고 있다. 간단하게 복습해보면 아래와 같다.

가령 아래와 같은 Row multiplication 행렬과 그 역행렬의 관계는 다음과 같다.

\[E=\begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{s} & 0 \\ 0 & 0 & 1\end{bmatrix} \rightarrow E^{-1}=\begin{bmatrix}1 & 0 & 0 \\ 0 & \color{red}{1/s} & 0 \\ 0 & 0 & 1\end{bmatrix}\]

와 같다.

또, 가령 아래와 같은 Row addition을 수행해주는 기본 행렬과 그 역행렬의 관계는 다음과 같다.

\[E=\begin{bmatrix}1 & 0 & 0 \\ \color{red}{s} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\rightarrow E^{-1}=\begin{bmatrix}1 & 0 & 0 \\ \color{red}{-s} & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\]

와 같다.

또, 행의 순서를 바꿔주는 기능을 수행해주는 기본 행렬과 그 역행렬의 관계는 다음과 같다.

\[P_{31}=\begin{bmatrix}0 & 0& \color{red}{1} \\ 0 & 1 & 0 \\ \color{blue}{1} & 0 & 0\end{bmatrix} \rightarrow P^{-1}_{31}=\begin{bmatrix}0 & 0& \color{red}{1} \\ 0 & 1 & 0 \\ \color{blue}{1} & 0 & 0\end{bmatrix}\]

그러므로 그림 2에서 볼 수 있었던 계수 행렬 $A$를 상삼각행렬로 만들어주는 연산에 대해 계수 행렬 $A$앞에 곱했던 기본행렬들의 역행렬을 순서대로 곱해주면 아래와 같이 행렬 $A$를 다시 써줄 수 있게 된다.

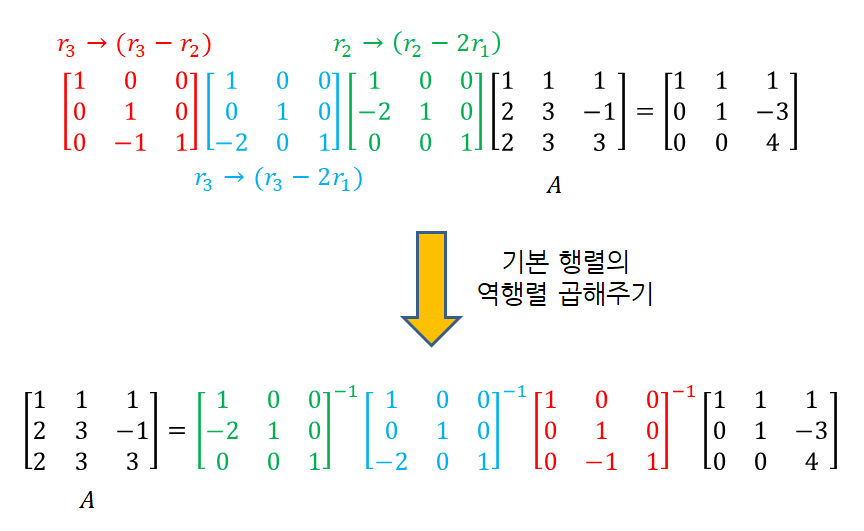
그림 3. 기본행렬들의 역행렬을 순서대로 다시 곱해줌으로써 좌변에 $A$만 남겨놓을 수 있게 된다.

그런 다음 기본 행렬의 역행렬들을 직접 계산해주고 행렬 곱을 통해 이들을 하나의 행렬로 합쳐주면 아래 그림과 같이 하삼각행렬로 합쳐질 수 있음을 알 수 있다.

따라서, 우리는 행렬 $A$를 하삼각행렬과 상삼각행렬의 곱으로 나눠줄 수 있다는 것을 알 수 있게 된다.

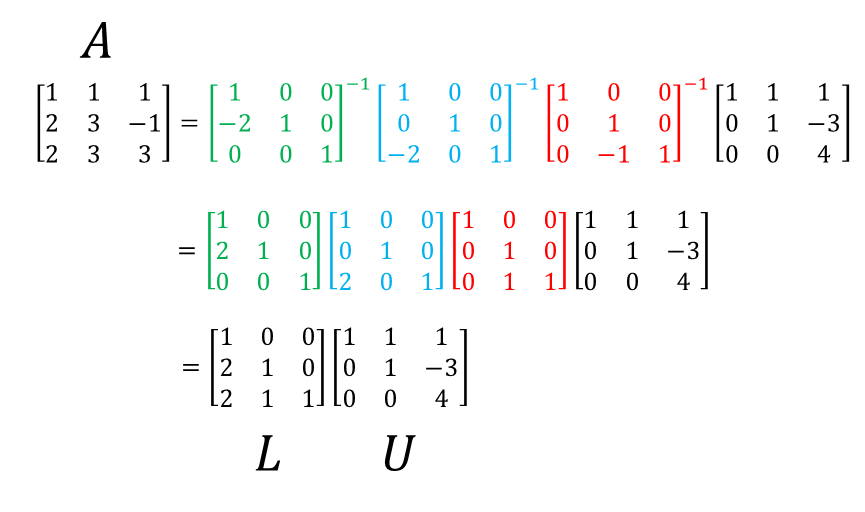
그림 4. 기본행렬들의 역행렬을 계산해주고 합쳐주면 행렬 $A$를 하삼각행렬과 상삼각행렬의 곱으로 나타내줄 수 있게 된다.

치환 행렬의 이용: PLU 분해

어떤 행렬은 행교환을 해주지 않으면 LU 분해가 바로 되지 않을 수 있다. 앞서 소개한 LU 분해의 예시에서는 사실 행 교환 연산은 이용하지 않은 경우였다. 이번에는 행 교환 연산까지도 포함되는 LU 분해를 생각해보자.

가령 아래와 같은 행렬 $A$를 생각해보자.

\[A = \begin{bmatrix}0& 0&3 \\ 1 & 1 & 1 \\ 2 & 3 & -1\end{bmatrix}\]

이런 행렬은 하삼각행렬 꼴의 기본행렬 중 row addition이나 row scaling 만을 이용해서는 최종 출력물이 상삼각행렬이 될 수 없다.

왜냐면 첫 번째 행에 첫 번째 두 번째 원소가 모두 0으로 이미 기정사실화 되어 있기 때문이다.

따라서, 하삼각행렬의 row addition과 row scaling에 해당하는 기본행렬만을 이용할 수 있도록 하기 위해선 $A$의 행을 바꿔놓고 시작해야만 한다.

이번 예시에서는 먼저 1행과 3행을 치환한 뒤 LU 분해를 생각해보자. 따라서

\[P_{13}=\begin{bmatrix}0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0\end{bmatrix}\]

이라는 행렬을 $A$에 곱해주면,

\[P_{13}A = \begin{bmatrix}2& 3&-1 \\ 1 & 1 & 1 \\ 0 & 0 & 3\end{bmatrix}\]

이 된다.

$r_2\rightarrow r_2-(1/2)r_1$ 연산을 수행해주면,

\[\Rightarrow \begin{bmatrix}1&0&0\\-1/2&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}2& 3&-1 \\ 1 & 1 & 1 \\ 0 & 0 & 3\end{bmatrix}=\begin{bmatrix}2& 3&-1 \\ 0 & -1/2 & 3/2 \\ 0 & 0 & 3\end{bmatrix}\]

와 같이 되는 것을 알 수 있으며 이 결과는 상삼각행렬임을 알 수 있다.

따라서, 기본 행연산의 역행렬을 취해 다음과 같이 써줄 수 있음을 생각해볼 수 있다.

\[P_{13}A = \begin{bmatrix}1&0&0\\-1/2&1&0\\0&0&1\end{bmatrix}^{-1}\begin{bmatrix}2& 3&-1 \\ 0 & -1/2 & 3/2 \\ 0 & 0 & 3\end{bmatrix}\] \[=\begin{bmatrix}1&0&0\\1/2&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}2& 3&-1 \\ 0 & -1/2 & 3/2 \\ 0 & 0 & 3\end{bmatrix}= LU\]

즉, 이와 같이 분해하고자 하는 행렬 $A$의 행순서를 미리 바꿔놓고 $LU$ 분해를 수행하는 경우를 PLU 분해를 수행한다고 한다.

앞서 언급했듯이 행 치환 행렬의 역행렬은 자기자신이므로 원래 계수행렬 $A$는 다음과 같이 분해할 수 있다.

\[A=\begin{bmatrix}0& 0&3 \\ 1 & 1 & 1 \\ 2 & 3 & -1\end{bmatrix}\] \[=P_{13}LU = \begin{bmatrix}0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0\end{bmatrix}\begin{bmatrix}1&0&0\\1/2&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}2& 3&-1 \\ 0 & -1/2 & 3/2 \\ 0 & 0 & 3\end{bmatrix}\]

LU 분해의 이용

LU 분해를 이용하면 어떤 이점이 있는지 생각해보자.

Ax=b의 해 구하기

만약 $A$가 정방행렬이고 $A=LU$와 같이분해 가능하다고 하면 다음과 같이 생각해볼 수 있다.

\[Ax=b\]

에서 $A=LU$라고 쓸 수 있으므로,

\[\Rightarrow (LU)x=b\]

이다. 이 때, 만약 이 식을 다음과 같이 괄호의 위치를 바꿔서 생각해보면,

\[\Rightarrow L(Ux)=b\]

$Ux$ 역시도 일종의 열벡터라고 생각할 수 있다는 것을 알 수 있다. 따라서, $Ux=c$라는 이름의 열벡터로 치환해주면,

\[\Rightarrow Lc=b\]

와 같은 꼴의 문제가 된다.

그런데, $L$은 잘 생각해보면 하삼각행렬이고 하삼각행렬은 forward substitution을 활용하면 solution을 수월하게 얻을 수 있다.

그런 다음 우리는

\[Ux=c\]

라는 문제를 풀어주면 $x$에 대한 답을 얻을 수 있게 되는 것이다. 이 때는 backward substitution을 써주면 해를 쉽게 얻을 수 있게 된다.

예를 들어, 위에서 보았던 행렬 $A$에 대해 LU 분해하면 다음과 같다.

\[A=LU\] \[\Rightarrow\begin{bmatrix}1&1&1\\ 2& 3& -1\\ 2&3&3\end{bmatrix}= \begin{bmatrix}1 & 0 & 0 \\2& 1 & 0\\2 & 1 & 1\end{bmatrix} \begin{bmatrix}1 & 1 & 1 \\0& 1 & -3\\0 & 0 & 4\end{bmatrix}\]

와 같은데,

$Ax=b$에서 $b$가 $[6, 5, 17]^T$ 였다고 하면, $LUx=b$는

\[\begin{bmatrix}1 & 0 & 0 \\2& 1 & 0\\2 & 1 & 1\end{bmatrix} \begin{bmatrix}1 & 1 & 1 \\0& 1 & -3\\0 & 0 & 4\end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}6\\5\\17\end{bmatrix}\]

과 같고, 위 식을 $Lc=b$의 꼴로 바꿔주면,

\[\begin{bmatrix}1 & 0 & 0 \\2& 1 & 0\\2 & 1 & 1\end{bmatrix} \begin{bmatrix}c_1\\c_2\\c_3\end{bmatrix}=\begin{bmatrix}6\\5\\17\end{bmatrix}\]

그러면 손쉽게 $c_1=6$, $c_2 = -7$, $c_3=12$라는 것을 알 수 있으므로 우리가 추가로 풀어야 할 문제는 $Ux=c$라는 점을 생각해보았을 때,

\[Ux=c\Rightarrow \begin{bmatrix}1 & 1 & 1 \\0& 1 & -3\\0 & 0 & 4\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix} = \begin{bmatrix}6\\-7\\12\end{bmatrix}\]

따라서, 이번엔 back-substitution을 이용하면 $z=3$, $y=2$, $x=1$ 임을 알 수 있다.

행렬식을 수월하게 구하기

마찬가지 원리로 만약 $A$라는 행렬이 LU 분해 가능하다고 하면 다음을 생각해볼 수 있다.

\[A=LU\]

라고 했을 때, 행렬식의 성질에 의해

\[det(A)=det(L)det(U)\]

일 것이다. 그런데 $L$이나 $U$는 모두 삼각행렬이므로 대각성분의 곱만으로 행렬식이 계산된다는 점을 생각하면 $A$의 행렬식을 쉽게 구할 수 있게 된다.

다시 말해 $A$를 분해한 $L$과 $U$가 식 (1), (2)와 같다고 하면 $A$의 행렬식은

\[det(A) = \prod_{i=1}^{n}l_{i,i}\prod_{j=1}^{n}u_{j,j}=\prod_{i=1}^{n}l_{i,i}u_{i,i}\]

와 같이 간단하게 계산할 수 있게 된다.