특이값 분해(SVD)가 말하는 것: 직교하는 벡터 집합에 대하여, 선형 변환 후에 그 크기는 변하지만 여전히 직교할 수 있게
되는 그 직교 집합은 무엇인가? 그리고 선형 변환 후의 결과는 무엇인가?

※ 특이값분해(Singular Value Decomposition, SVD)는 보통 복소수 공간에 대하여 정의하는 것이 일반적이지만, 본 페이지에서는 실수 벡터 공간에 한정하여 작성되어 있음을 명시합니다.

※ 본 article에서는 열벡터(column vector) convention을 따릅니다.

특이값분해의 정의

특이값 분해(Singular Value Decomposition, SVD)는 임의의 $m\times n$차원의 행렬 $A$에 대하여 다음과 같이 행렬을 분해할 수 있다는 ‘행렬 분해(decomposition)’ 방법 중 하나이다.

\[A = U \Sigma V^T\]

여기서 네 행렬($A, U, \Sigma, V$)의 크기(혹은 차원)와 성질은 다음과 같다.

$A$: $m\times n$ rectangular matrix
$U$: $m\times m$ orthogonal matrix
$\Sigma$: $m\times n$ diagonal matrix
$V$: $n\times n$ orthogonal matrix

---

여기서 약간의 보충 설명을 위해 orthogonal matrix와 diagonal matrix에 대한 성질을 추가하여 적자면 다음과 같다.

orthogonal matrix는 다음의 성질을 만족하는 행렬이다.

$U$가 orthogonal matrix라고 한다면,

\[UU^T=U^TU=I\]

이에 따라, $U^{-1}=U^T$라는 사실도 부가적으로 확인된다.

---

또, diagonal matrix는 다음과 같은 성질을 만족하는 행렬이다.

$\Sigma$가 diagonal matrix라고 한다면 $\Sigma$의 대각성분을 제외한 나머지 원소의 값은

모두 0이다.

즉, $\Sigma$가 $2\times 2$ 행렬일 때 대략적으로 다음과 같은 모양을 가진다.

\[\begin{pmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \end{pmatrix}\]

또, 만약 $\Sigma$가 $m\times n$ 행렬일 때, $m>n$이라면 대략적으로 다음과 같은 모양을 가진다.

\[\begin{pmatrix} \sigma_1 & 0 & \cdots & 0 \\\\ 0 & \sigma_2 & \cdots & 0 \\\\ {} & {}& \ddots & {} \\\\ 0 & 0 & \cdots & \ \sigma_n \\\\ 0 & 0 & \cdots & \ 0 \\\\ \vdots & \vdots & \vdots & \vdots \\\\ 0 & 0 & \cdots & 0 \end{pmatrix}\]

또, 만약 $\Sigma$가 $m\times n$ 행렬일 때, $m<n$이라면 대략적으로 다음과 같은 모양을 가진다.

\[\begin{pmatrix} \sigma_1 & 0 & \cdots & 0 &0 & \cdots & 0 \\\\ 0 & \sigma_2 & \cdots & 0 & 0 & \cdots & 0\\\\ {} & {}& \ddots & {} & {} & {} & {}\\\\ 0 & 0 & \cdots & \ \sigma_m & 0 & \cdots & 0 \end{pmatrix}\]

특이값 분해의 기하학적 의미

특이값 분해는 다음과 같은 의미를 갖는다.

$\Rightarrow$ 직교하는 벡터 집합에 대하여, 선형 변환 후에 그 크기는 변하지만 여전히 직교할 수 있게 되는 그 직교 집합은 무엇인가? 그리고 선형 변환 후의 결과는 무엇인가?

2차원 벡터공간에서 …

설명을 단순화 시키고, 시각적인 설명을 할 수 있도록 행렬 $A$가 $2\times 2$ 차원인 경우에 한정하여 생각해보자.

우리는 2차원 실수 벡터 공간에서 하나의 벡터가 주어지면 언제나 그 벡터에 직교하는 벡터를 찾을 수 있다.

좀 더 정형화된 방법은 Gram-Schmidt 과정을 이용하면 더 정교하게 찾을 수도 있을 것이다.

그런데, 직교하는 두 벡터에 대해 동일한 선형 변환 A를 취해준다고 했을 때, 그 변환 후에도

여전히 직교한다고 보장할 수는 없다.

아래 그림은 행렬 A에 대하여,

\[A=\begin{pmatrix} 0.25 & 0.75 \\ 1 & 0.5 \end{pmatrix}\]

임의의 벡터 $\vec x$를 선형변환 시켰을 때의 결과($A\vec x$)를 보여주고 있다.

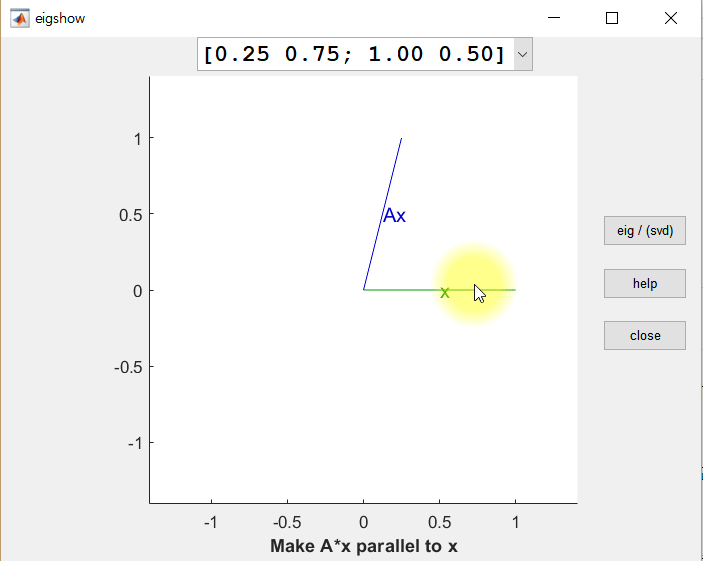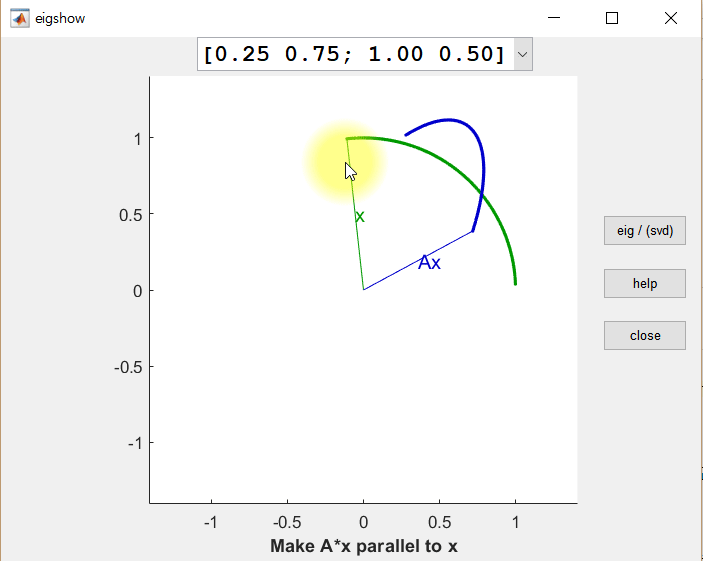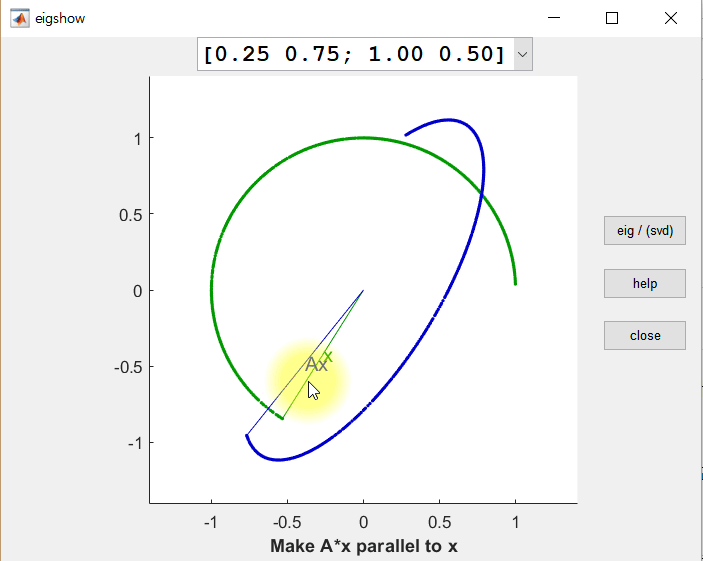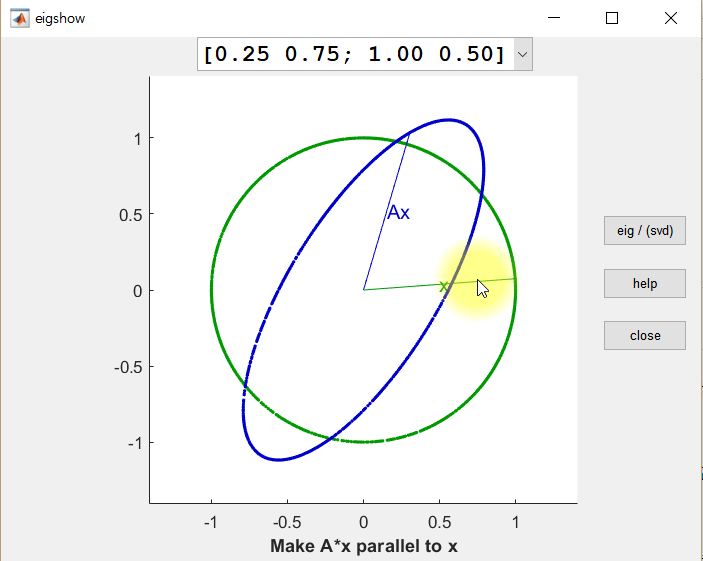
그림 1. 임의의 벡터 x와 어떤 행렬 A를 이용해 선형변환 시킨 결과 Ax

그렇다면, 직교하는 두 벡터에 대해 동시에 선형 변환을 시켜본다면, 선형 변환 후의 결과가

직교하는 경우를 찾을 수 있을까? 아래의 그림은 동일한 행렬 $A$에 대하여 직교하는 두 벡터 $\vec x$와 $\vec y$에 대한 선형 변환 결과(각각 $A\vec x$, $A\vec y$)를 보여준다.

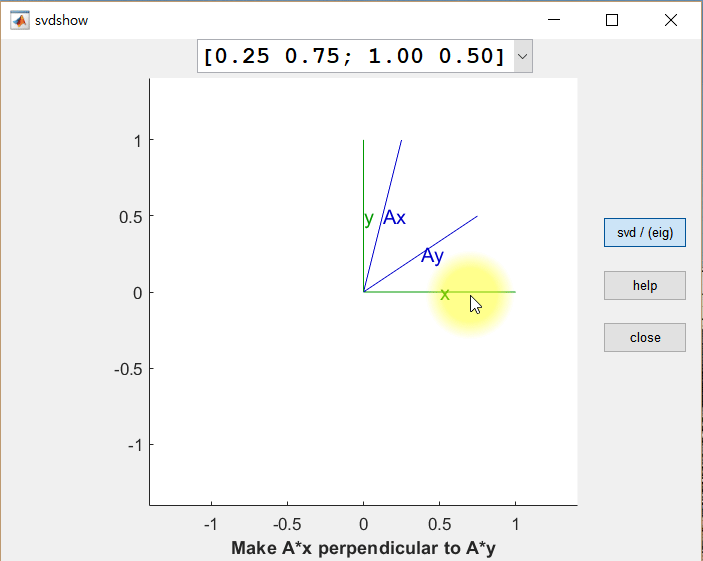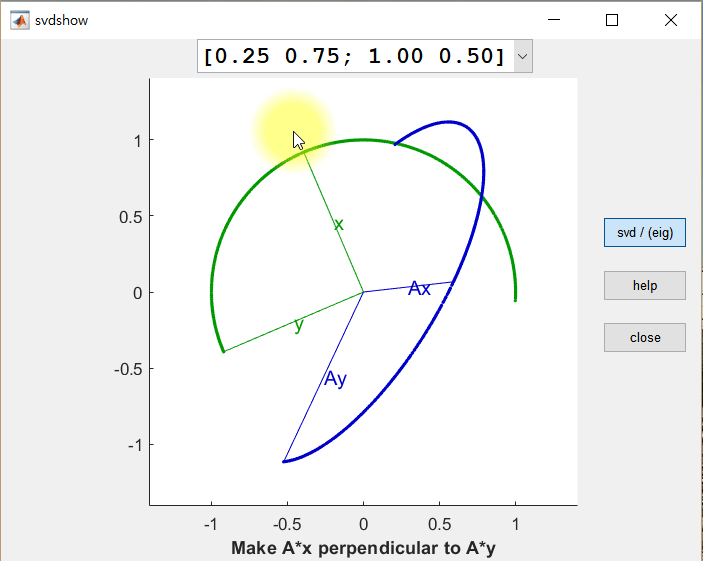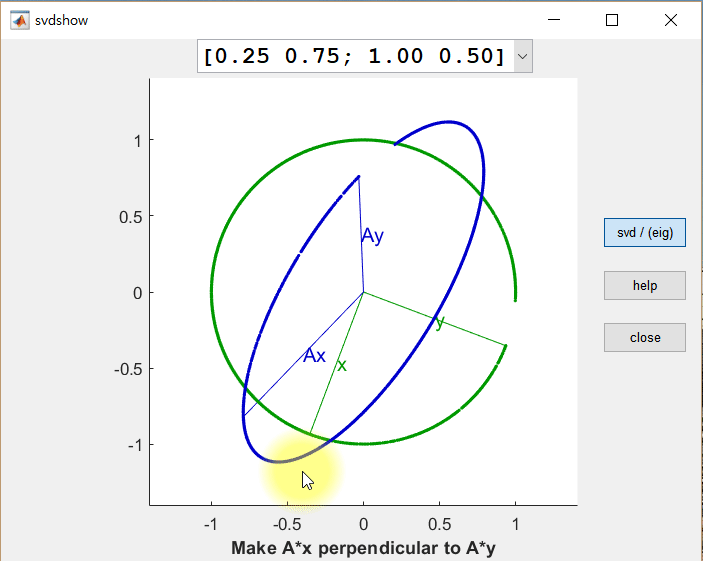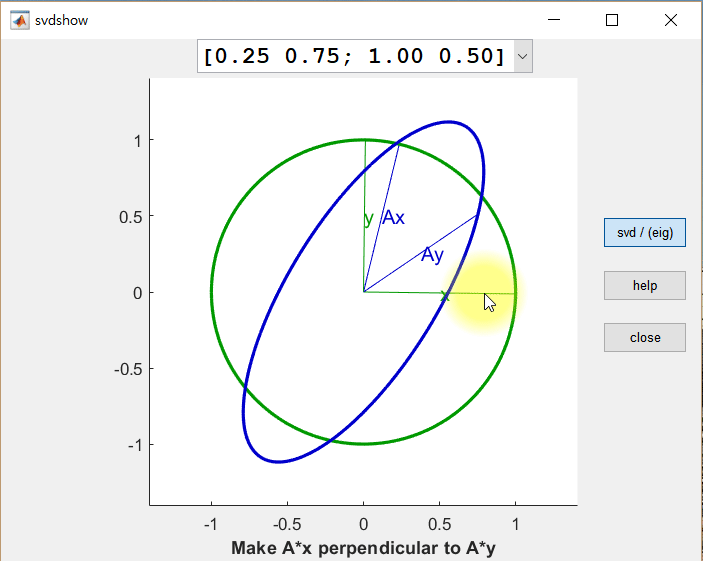
그림 2. 임의의 벡터 x와 x에 직교하는 벡터 y, 그리고 x, y를 선형변환한 결과인 Ax와 Ay

위 그림에서 주목할 것은 크게 두 가지이다.

$A\vec x$와 $A\vec y$가 직교하게 되는 경우는 단 한번만 있는 것이 아님을 확인할 수 있다.

또, $A\vec x$와 $A\vec y$는 $A$라는 행렬(즉, 선형변환)을 통해 변환되었을 때, 길이가 조금씩 변했다는 것이다. 이 값들을 scaling factor라고 할 수 있지만, 일반적으로는 singular value라고 하고 크기가 큰 값부터 $\sigma_1, \sigma_2, \cdots$ 등으로 부른다.

처음으로 돌아가서, 임의의 $m\times n$행렬 $A$는 다음과 같이 분해된다고 했다.

\[A=U\Sigma V^T\]

위의 예시에서 보여준 선형 변환 전의 직교하는 벡터 $\vec x, \vec y$는 다음과 같이 열벡터의 모음으로 생각할 수 있으며 이것이 $A=U\Sigma V^T$에서 $V$행렬에 해당된다.

\[V= \begin{pmatrix} | & | \\\\ \vec x & \vec y \\\\ | & | \end{pmatrix}\]

또, 위 예시에서 보여준 선형 변환 후의 직교하는 벡터 $A\vec x, A\vec y$에 대하여 각각의 크기를 1로 정규화한 벡터를 $\vec u_1$, $\vec u_2$라 한다면 이 둘의 열 벡터의 모음이 $A=U\Sigma V^T$에서 $U$행렬에 해당된다.

\[U= \begin{pmatrix} | & | \\\\ \vec u_1 & \vec u_2 \\\\ | & | \end{pmatrix}\]

마지막으로 singular value(즉, scaling factor)는 다음과 같이 $\Sigma$ 행렬로 묶어서 생각할 수 있다.

\[\Sigma= \begin{pmatrix} \sigma_1 & 0 \\\\ 0 & \sigma_2 \end{pmatrix}\]

선형 변환의 관점에서 네 개의 행렬($A, V, \Sigma, U$)의 관계를 생각하면 다음과 같다.

\[AV=U\Sigma\]

즉, “$V$에 있는 열벡터($\vec x$ 혹은 $\vec y$)를 행렬 $A$를 통해 선형변환 할 때, 그 크기는 $\sigma_1$, $\sigma_2$만큼 변하지만,

여전히 직교하는 벡터들 $\vec u_1$, $\vec u_2$를 찾을 수 있겠느냐?” 라고 묻는 것이다.

그러면 $V$는 orthogonal matrix이므로 $V^{-1}=V^T$이기 때문에,

\[AV=U\Sigma\] \[AVV^T=U\Sigma V^T\] \[A=U\Sigma V^T\]

라는 관계가 성립한다.

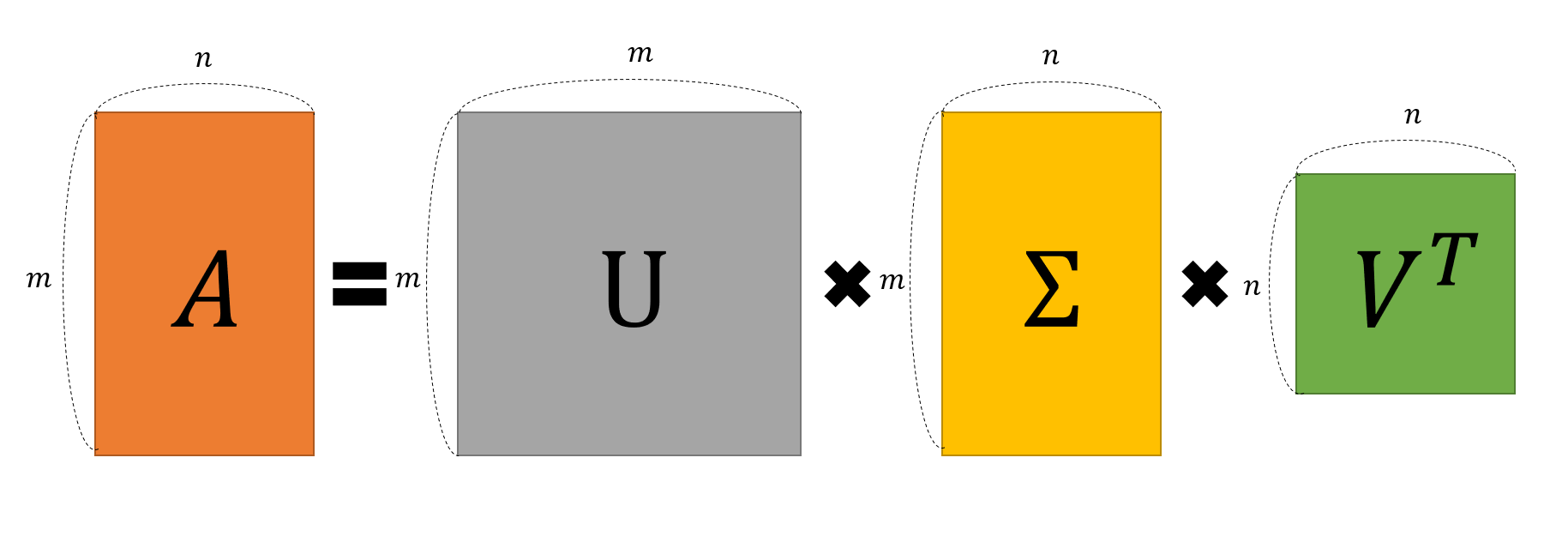
그림 3. 임의의 행렬 A를 특이값 분해한 결과를 시각화한 것.

입-출력의 차원이 다른 변환인 경우는?

특이값분해를 정의할 때 분해되는 행렬 $A$는 $m\times n$차원이라고 하였다.

즉, square matrix가 아닌 경우에도 행렬 A는 분해될 수 있다.

---

차원이 감소되는 경우를 생각하면 이해가 쉬운데,

가령 우리의 행렬 $A$가 3차원에서 2차원으로 차원을 낮춰주는 $2\times 3$행렬이라고 하자.

그렇다면 특이값분해(SVD)가 요구하는 것을 다시 생각해본다면,

3차원 공간에서 직교하던 세 벡터를 선형변환 하여 2차원으로 변환한 뒤에도,

2차원 공간에서 두 개의 벡터가 직교할 수 있게 만들 수 있겠느냐?는 것을 묻고 있다고 할 수 있다.

아래의 움직이는 그림을 보자. 아래의 그림은 3차원 벡터 공간에서 2차원 벡터공간(즉, 평면)으로의

선형변환을 표현하고 있다¹.

영상에 대해 약간 부연설명을 하자면, 색깔로 표시된 공들은 3차원 공간 상의 벡터이다.

보통은 화살표로 표시하지만, 머리부분만을 동그랗게 표현했다고 생각하면 된다.

이 영상에서 보여주는 변환은 3차원 벡터들을 평면 상에 사영시키는 변환이다.

이 경우 특이값 분해를 실시하면 선형변환 전 직교하는 벡터와 선형변환 후 직교하는 벡터는

다음과 시각화 할 수 있다.

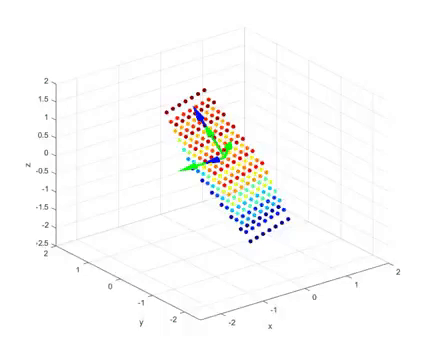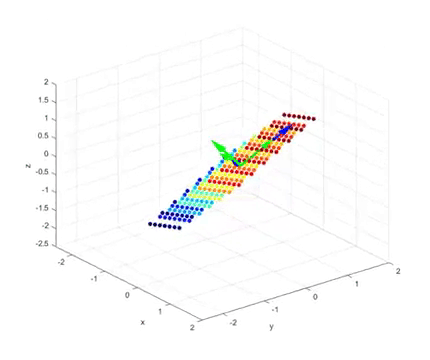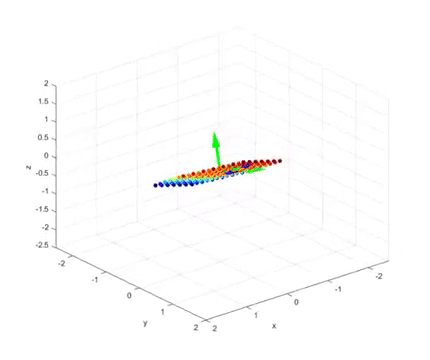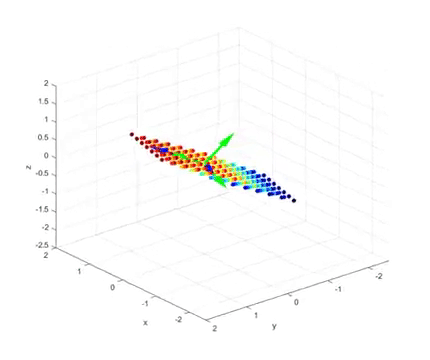
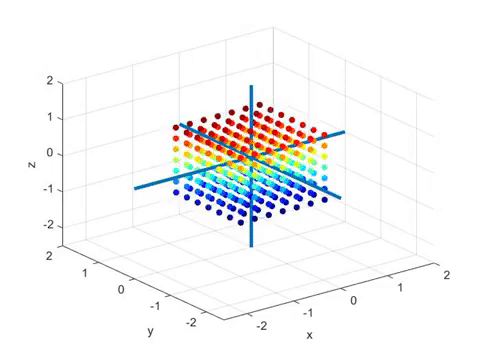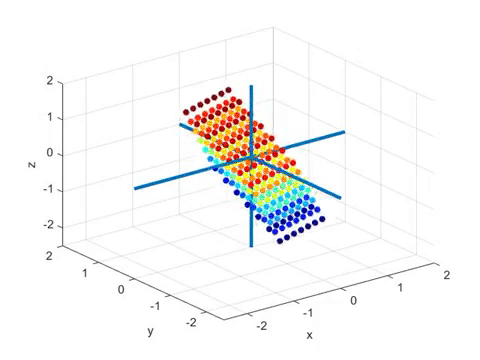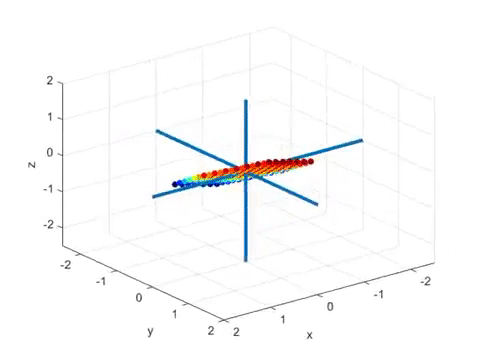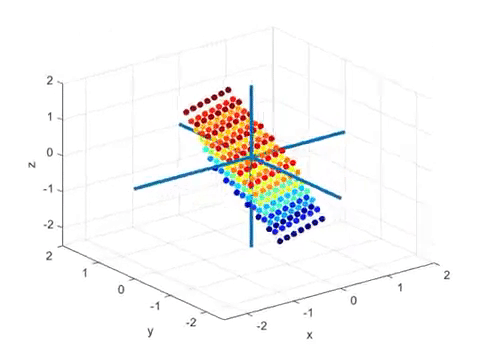
영상의 마지막 부분을 보면 다음과 같은데,

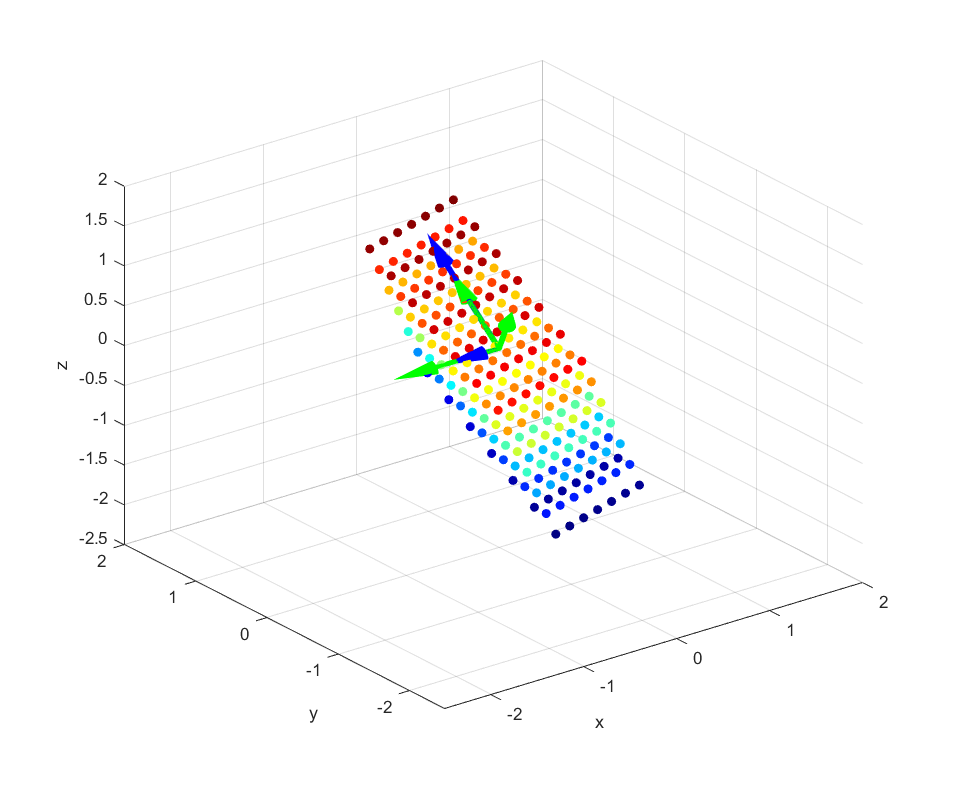
그림 4. 2 x 3 행렬의 선형 변환 후의 결과 및 V 행렬의 역벡터(초록)와 U 행렬의 열벡터(파랑)

여기서 초록색 화살표로 표시한 벡터들은 선형변환 전의 직교하는 벡터들이고

파란색 화살표로 표시한 벡터들은 선형 변환 후에 직교하는 벡터들이다.

이처럼 선형 변환 전 벡터들 중 하나의 scaling factor(즉, singular value)를 0으로 만듦으로써

차원이 변하는 선형변환의 경우에도 특이값 분해가 가능하다.

특이값 분해의 목적

특이값 분해의 공식을 다시 풀어 써보자면 다음과 같다.

\[A = U\Sigma V^T\] \[= \begin{pmatrix} | & | & {} & | \\\\ \vec u_1 & \vec u_2 &\cdots &\vec u_m \\\\ | & | & {} &| \end{pmatrix} \begin{pmatrix} \sigma_1 & & & & 0\\\\ & \sigma_2 & & & 0\\\\ & & \ddots & & 0\\\\ & & & \sigma_m & 0 \end{pmatrix} \begin{pmatrix} - & \vec v^T_1 & - \\\\ - & \vec v^T_2 & - \\\\ &\vdots& \\\\ - & \vec v^T_n & - \end{pmatrix}\] \[= \sigma_1 \vec u_1 \vec v_1^T + \sigma_2 \vec u_2 \vec v_2^T +\cdots+ \sigma_m \vec u_m \vec v_m^T\]

여기서 $\vec u_1 \vec v_1^T$ 등은 $m\times n$ 행렬이된다. 또, $\vec u$와 $\vec v$는 정규화된 벡터이기 때문에 $\vec u_1 \vec v_1^T$ 내의 성분의 값은 -1에서 1사이의 값을 가진다.

따라서, $\sigma_1 \vec u_1 \vec v_1^T$라는 부분만을 놓고 보면, 이 행렬의 크기는 $\sigma_1$의 값에 의해 정해지게 된다.

즉, 우리는 SVD라는 방법을 이용해 A라는 임의의 행렬을 여러개의 A 행렬과 동일한 크기를 갖는 여러개의 행렬로 분해해서 생각할 수 있는데, 분해된 각 행렬의 원소의 값의 크기는 $\sigma$의 값의 크기에 의해 결정된다.

다시 말해, SVD를 이용해 임의의 행렬 A를 정보량에 따라 여러 layer로 쪼개서 생각할 수 있게 해준다.

특이값 분해의 활용

특이값 분해는 분해되는 과정보다는 분해된 행렬을 다시 조합하는 과정에서 그 응용력이 빛을 발한다.

기존의 $U, \Sigma, V^T$로 분해되어 있던 $A$행렬을 특이값 p개만을 이용해 A’라는 행렬로 ‘부분 복원’ 할 수 있다. 위에서 말했던 것 특이값의 크기에 따라 A의 정보량이 결정되기 때문에 값이 큰 몇 개의 특이값들을 가지고도 충분히 유용한 정보를 유지할 수 있다.

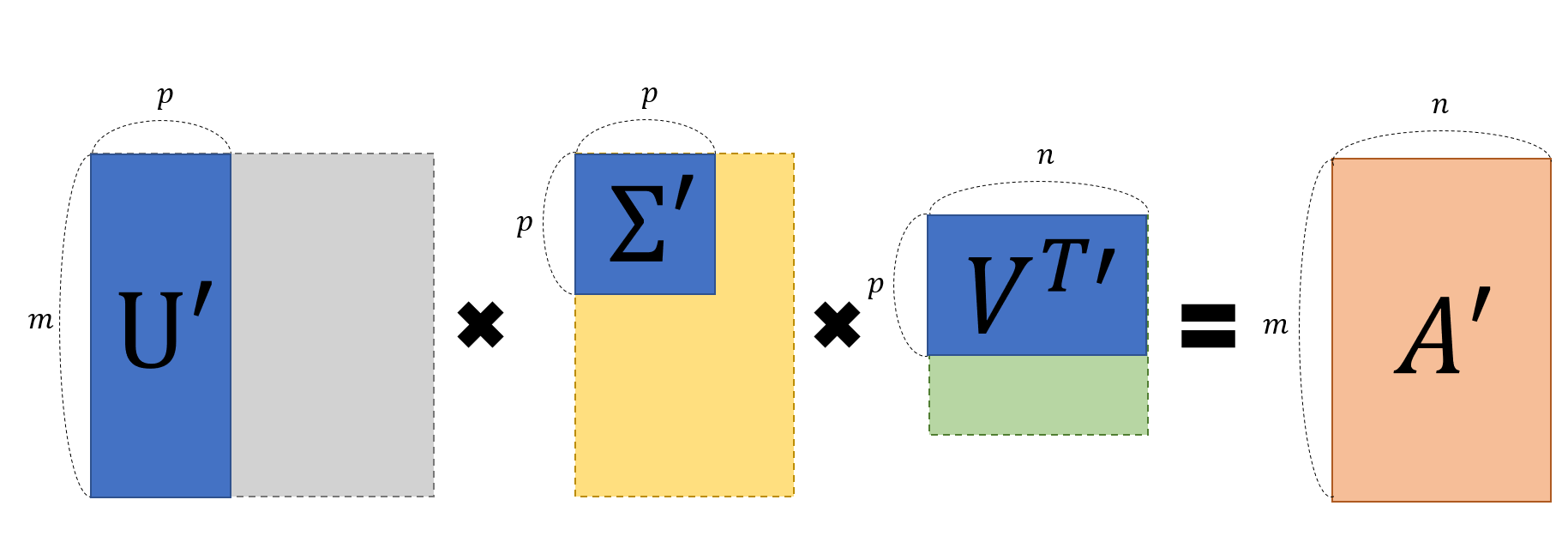
그림 5. 특이값 분해를 통해 얻어진 U, Sigma, V 행렬에서 일부만을 이용해 적당한 A'를 부분복원 하는 과정

아래의 애플릿에서는 해당 ‘부분 복원’ 과정을 사진을 통해 확인해볼 수 있다. 최대한 중요한 정보들만 부분 복원해서 사용하면 사진의 용량은 줄어들지만 여전히 사진이 보여주고자 하는 내용은 살릴 수 있을 것이다.