행렬은 선형 변환이다.
임의의 벡터 $\vec a$, $\vec b$와 스칼라 $c$ 에 대하여 변환 $T$ 가 다음의 두 조건을 만족한다면 이 변환 $T$ 는 선형변환이다.
\[T(\vec a + \vec b) = T(\vec a)+T(\vec b)\] \[T(c \vec a) = c T(\vec a)\]따라서, 위의 선형 변환의 성질에 따라, 임의의 벡터
\[\left[ \begin{array}{c} x\\ y \end{array} \right]\]에 대해 다음이 성립한다.
\[T \left ( \begin{bmatrix}x \\ y \end{bmatrix} \right ) = T\left ( x \begin{bmatrix}1 \\ 0 \end{bmatrix} + y \begin{bmatrix}0 \\ 1 \end{bmatrix} \right ) = x T \left ( \begin{bmatrix}1 \\ 0 \end{bmatrix} \right ) + y T\left ( \begin{bmatrix}0 \\ 1 \end{bmatrix} \right )\]여기서 눈여겨 볼 점은, 원래의 기저 벡터 두 개를 아래와 같이 $\hat{i}$, $\hat{j}$ 라 하고,
\[\hat i = \begin{bmatrix}1 \\ 0 \end{bmatrix}\] \[\hat j = \begin{bmatrix}0 \\ 1 \end{bmatrix}\]새로운 기저 벡터를 $\hat i_{new}$, $\hat j_{new}$ 라 했을 때,
\[\hat i_{new} = T\left ( \begin{bmatrix}1 \\ 0 \end{bmatrix} \right )\] \[\hat j_{new} = T\left ( \begin{bmatrix}0 \\ 1 \end{bmatrix} \right )\]$T$ 가 선형변환이라면, 벡터 $\begin{bmatrix}x \ y \end{bmatrix}$ 는 선형 변환 후에
새로운 기저 벡터 $\hat i_{new}$ 와 $\hat j_{new}$ 의 $x$ 배와 $y$ 배의 합으로 표현되어야 한다는 것이다.
예를 들어, 행렬
\[A=\begin{bmatrix} 2 & -3 \\ 1 & 1 \end{bmatrix}\]를 이용해 벡터
\[\vec x=\begin{bmatrix} 1 \\ 1 \end{bmatrix}\]를 변환시켜 보면,
\[A\vec x =\begin{bmatrix} 2 & -3 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix}=\begin{bmatrix} -1 \\ 2 \end{bmatrix}\]임을 알 수 있는데, 아래의 영상에서 처럼 이 값은 새로운 두 기저벡터의 1배와 1배의 합으로 표현될 수 있다.
위 애플릿의 슬라이드를 가장 오른쪽으로 옮겼을 때의 결과는 다음과 같은데,
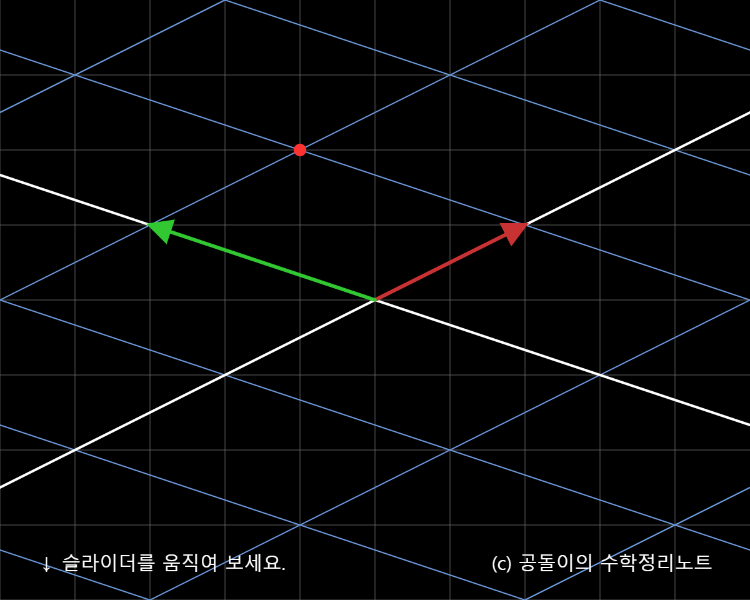
이를 보면 선형 변환의 결과로써의 빨간 점은 원래 기저 벡터의 -1, 2 배로 표현되었지만,
선형 변환 이후의 새로운 기저 벡터 $\hat i_{new}$, $\hat j_{new}$에 대해서는 각각 1,1 배로 표현되는 것을 알 수 있다.
일반적으로, 선형대수학의 기본 정리에 따르면 벡터 공간의 선형 변환과 행렬은 본질적으로 같다.
여러 선형 변환의 시각적 예시
위 영상 및 그림에서 또 한가지 눈여겨 볼 점은 선형 변환이라는 것은 기하학적으로 표현하자면, 격자들이 변환 후에도
선의 형태이고, 격자 간의 간격도 균등하게 넓어야 한다는 것이다.
여러가지 선형 변환(즉, 행렬)을 기하학적으로 시각화 하였으니,
이를 확인해봄으로써 격자들이 변환 후에도 선의 형태를 유지하면서도, 격자 간의 간격이 균등하게 넓은지 확인해보자.