Prerequisites
이번 포스팅을 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
Unit impulse function
이번 포스팅에서는 이산 컨볼루션에 대해 주로 알아보고자 한다. 그런데, 이산 컨볼루션을 생각 해보기에 앞서 단순하지만 아주 중요한 함수 하나를 생각해보자.
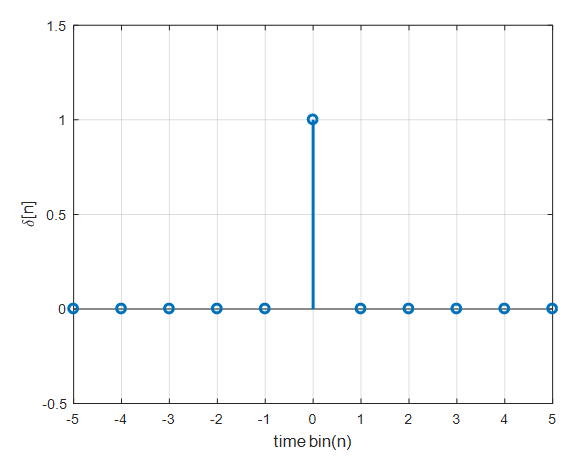
그림 1. 단위 임펄스(unit impulse) 함수
위 그림과 같이 정의된 함수를 단위 임펄스(unit impulse) 함수라고 부른다. 단위 임펄스 함수의 정의는 다음과 같다.
\[\delta[n]=\begin{cases}1, &\text{if } n=0 \\ 0, & \text{otherwise}\end{cases}\]단위 임펄스 함수는 수에서 1과 같은 역할을 한다. 또, 벡터에서는 단위 기저벡터와 같은 역할을 한다.
이산 컨볼루션
이산 컨볼루션의 유도
단위 임펄스는 좌, 우로 평행이동이 가능하다. 가령, $\delta[n-2]$는 $\delta[n]$을 오른족으로 2만큼 shift 시킨 것이다.
이 개념을 조금만 더 확장해보면 임펄스를 이용해 임의의 신호를 분해해 표현할 수 있게 된다. 아래의 임의의 이산 신호 $x[n]$을 보자.
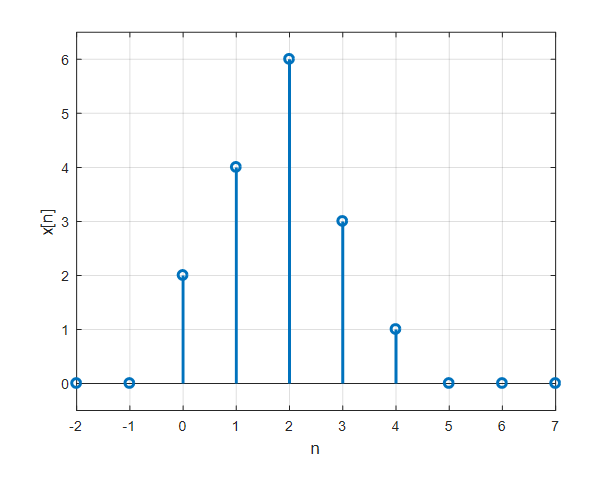
그림 2. 임의의 이산 신호 $x[n]$
이 이산신호는 $\delta[n]$ 및 이것을 좌우로 shift한 함수들을 이용해 다음과 같이 표현할 수 있다.
\[x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]\] \[=\cdots + x[-2]\delta[n+2]+x[-1]\delta[n+1]+x[0]\delta[n]+x[1]\delta[n-1]+x[2]\delta[n-2]+\cdots\]즉, $x[n]$ 이라는 임의의 함수를 $\delta [n-k]$ 라는 함수를 이용해서 분해할 수 있다.
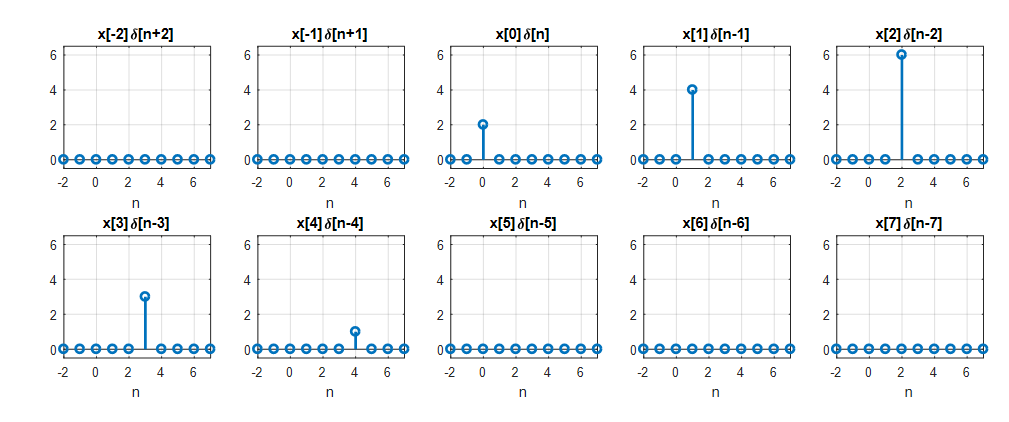
그림 3. 임의의 이산함수 $x[n]$를 단위 임펄스 함수를 이용해 분해한 결과
식 (3)은 $x[n]$을 단위 임펄스 함수로 분해한 것으로 볼 수도 있고, 상수가 곱해진 신호열의 합으로 볼 수도 있다.
여기서 상수는 $x[k]$를 의미한다. $x[k]$는 $k$번째 함수값이라는 의미이기 때문에 더 이상 함수가 아닌 상수이다.
식 (3)은 다음과 같이 기호로 표기하기도 한다.
\[\Rightarrow x[n] * \delta[n]\]이 때, $*$ 연산을 컨볼루션이라고 부르기도 한다.
일반적으로 임의의 이산 함수 $x[n]$과 $h[n]$에 대해 두 함수의 컨볼루션은 다음과 같다.
\[x[n] * h[n] = \sum_{k=-\infty}^{\infty}x[k]h[n-k]\]LTI 시스템과 컨볼루션
입력 $x[n]$ 과 출력 $y[n]$ 의 관계를 다음과 같이 생각해보자. 출력 $y[n]$ 을 입력 $x[n]$ 의 어떠한 변환이라고 생각한다면, $y[n]=T \left(x[n] \right)$ 이라고 생각할 수 있다.
만약, 현재 고려하는 시스템이 LTI 시스템이라고 한다면 선형성에 의해 다음이 성립한다.
\[T\left( \sum_{k=-\infty}^{\infty}c_kx_k[n]\right) = \sum_{k=-\infty}^{\infty}{c_kT(x_k[n])}=\sum_{k=-\infty}^{\infty}{c_ky_k[n]}\]또, 시불변성에 의해 다음이 성립한다.
\[T \left(x[n-k] \right)=y[n-k]\]그렇다면, 다시 한번 식 (3)을 이용하여 아래의 식을 좀 더 전개해보자.
\[y[n] =T(x[n])\notag\] \[=T\left(\cdots + x[-2]\delta[n+2]+x[-1]\delta[n+1]+x[0]\delta[n]+x[1]\delta[n-1]+x[2]\delta[n-2]+\cdots \right)\] \[=T\left( \sum_{k=-\infty}^{\infty}{x[k]\delta[n-k]}\right)\]이 때, $x[k]$ 는 $n$에 대해서는 함수가 아닌 상수이기 때문에 선형성에 의해서 위 식은 다음과 같다.
\[\Rightarrow \sum_{k=-\infty}^{\infty}{\left(x[k]T\left(\delta[n-k]\right) \right)}\]라고 할 수 있다. 이 때, $h[n]=T\left(\delta[n]\right)$ 라고 하자.
그러면 시불변성에 의해서
\[\Rightarrow \sum_{k=-\infty}^{\infty}{\left(x[k]T\left(\delta[n-k]\right) \right)} = \sum_{k=-\infty}^{\infty}{x[k]h[n-k]}\]라는 수식을 만족할 수 있다.
다시 한번, 위 식은 $y[n]$ 과 같으므로,
\[y[n] = \sum_{k=-\infty}^{\infty}{x[k]h[n-k]}\]라고 할 수 있다.
여기서 $h[n] = T\left(\delta[n]\right)$는 $\delta[n]$을 입력으로 했을 때의 변환이므로 해당 시스템에 대해 임펄스 입력을 줬을 때의 응답이다. 이를 임펄스 응답이라고 부른다.
다시 말해 다루고자 하는 시스템이 LTI 시스템이라면 입력과 임펄스 응답($h[n]$)의 이산 컨볼루션으로 시스템의 입출력 관계를 표현할 수 있다.
이산 컨볼루션의 성질
교환 법칙
컨볼루션은 두 신호 $x[n]$과 $h[n]$에 대해 다음과 같이 교환 법칙이 성립한다.
\[x[n] * h[n] = h[n] * x[n]\]식 (5)의 컨볼루션의 정의를 보면 한쪽 신호를 뒤집어 줘서 합해주는 것을 알 수 있는데, 교환 법칙이 성립한다는 것은 두 신호 중 어떤 것을 뒤집더라도 결과는 같다는 것을 말해준다.
즉, 계산이 편해지는 쪽의 신호를 뒤집어서 연산을 수행해주면 된다.
이를 시스템적인 관점에서 접근하자면 입력 신호와 시스템의 임펄스 응답의 역할을 바꾸어도 시스템의 출력이 여전히 같다는 것을 의미한다.
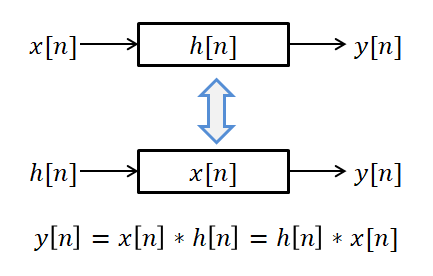
그림 4. 이산 컨볼루션의 교환 법칙이 성립한다는 것은 입력 신호와 임펄스 응답의 역할이 바뀌어도 시스템은 출력이 유지된다는 것을 의미한다.
또, 다른 해석으로는 두 개의 시스템이 직렬로 연결되는 경우 연결 순서를 바꾸어도 전체 시스템은 동일하다는 것 또한 생각해볼 수 있다.
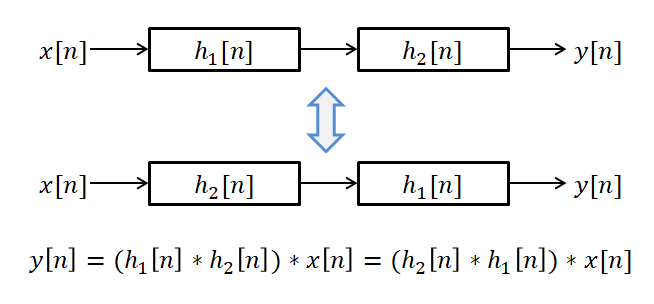
그림 5. 이산 컨볼루션의 교환 법칙이 성립한다는 것은 연속 적용되는 시스템의 순서를 바꾸어도 전체 시스템은 동일하다는 것을 의미한다.
결합 법칙
컨볼루션은 셋 또는 그 이상의 신호에 대해 조합된 컨볼루션의 계산 순서에 영향을 받지 않는다.
\[(x[n] * h_1[n]) * h_2[n] = x[n] * (h_1[n] * h_2[n])\]예를 들어 두 개의 시스템이 직렬로 연결되어 있는 경우, 두 개의 시스템을 컨볼루션으로 결합한 시스템 하나로 두 개 시스템의 결합을 대체할 수 있다는 것을 의미한다.
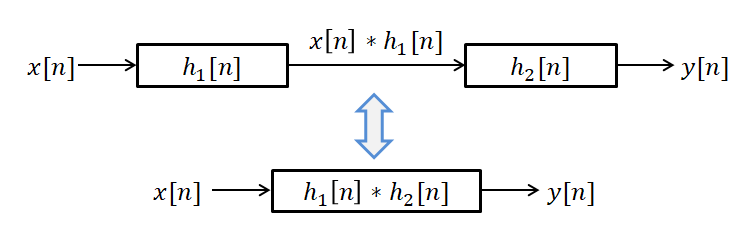
그림 6. 이산 컨볼루션의 결합 법칙의 의미. 두 시스템을 컨볼루션으로 합쳐 하나의 시스템처럼 다룰 수 있다.
분배 법칙
컨볼루션 연산은 다음과 같이 덧셈에 대한 분배법칙을 만족한다.
\[x[n]*(h_1[n] + h_2[n])= x[n]*h_1[n] + x[n]*h_2[n]\]분배 법칙은 두 개의 시스템이 병렬로 연결되어 있을 경우 각 시스템의 임펄스 응답을 더한 것으로 전체 시스템을 대체할 수 있다는 것을 의미한다.
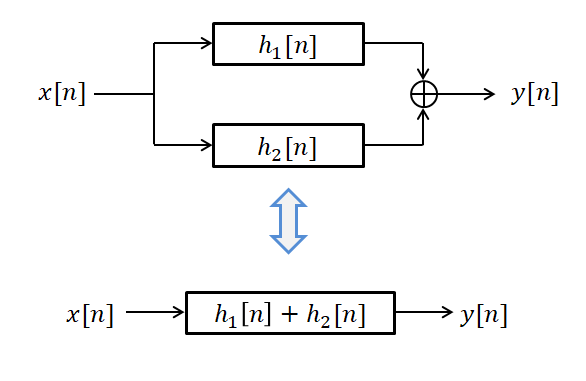
그림 7. 이산 컨볼루션의 분배 법칙의 의미.
임펄스 응답
임펄스 응답의 물리적 의미
임펄스 응답은 이산 컨볼루션을 유도해내는 과정에서 나오게된 결과로써, 임펄스를 입력으로 줬을 때 시스템에서 보여주는 출력이다.
하지만, 임펄스 응답은 이보다 더 큰 의미를 갖는다. 임펄스 응답은 과거의 입력 값들이 현재의 출력 값에 기여하는 정도가 얼마인지 알려주는 가중치의 역할을 한다.
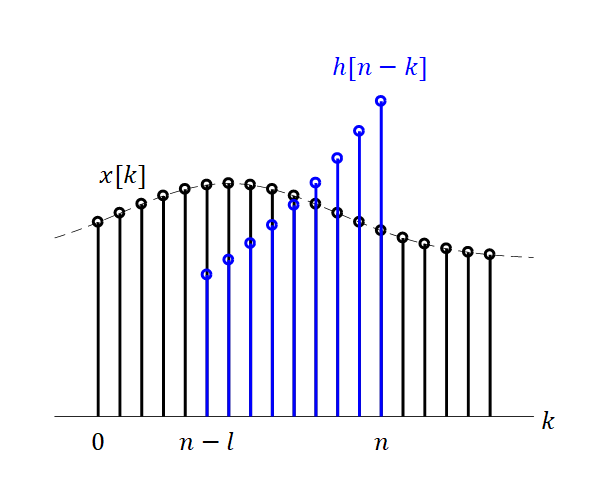
그림 8. 임펄스 응답의 물리적 의미
그러다보니 임펄스 응답 하나만을 가지고 시스템의 특성을 파악할 수 있다.
또, 임펄스를 입력으로 넣어주는 것은 시스템에 일종의 시동을 걸어주는 것 처럼 볼 수 있다. $n=0$인 시점에 임펄스 입력을 넣어줌으로써 $n>0$ 인 시점에서 시스템이 작동하는데,
이것은 외부 입력에 의한 응답이라기 보다는 시스템의 내부적인 특성을 반영한 출력이기 때문에 시스템의 특성에 관한 정보를 임펄스 응답을 통해서 알 수 있게 되는 것이다.
임펄스 응답과 시스템의 특성
앞서 선형 시불변(LTI) 시스템 편에서는 선형, 시불변 시스템에 대해서 알아보았는데, 이 외에도 여러가지 시스템의 특성이라 할 수 있는 것들이 있다.
순시적 시스템과 동적 시스템
순시적(instantaneous) 시스템은 현재 들어오는 입력에 의해서만 결정되는 시스템을 말한다. 반면 동적(dynamic) 시스템은 과거의 출력이나 입력에 의해서도 영향을 받을 수 있다.
순시적 시스템은 가령 아래와 같은 시스템이다.
\[y[n]=3x[n]\]여기서 임펄스 응답은 $h[n]=3$이 될 것이다.
반면 동적 시스템은 가령 다음과 같은 것이다.
\[y[n]=\frac{1}{2}(x[n]+x[n-1])\]이 경우의 임펄스 응답은 아래와 같다. (왜 그런지는 아래의 문제에서 풀어보게 될 것이다.)
\[h[n]=\frac{1}{2}(\delta[n]+\delta[n-1])=\begin{cases} 0.5 & n = 0, 1 \\ 0 & \text{otherwise} \end{cases}\]인과 시스템과 비인과 시스템
인과(causal) 시스템은 현재 입력이 있어야만 출력이 나오는 시스템이다. 다시 말하면 입력을 넣어주기 전에는 출력이 0이다. 즉, $k \lt 0$ 조건에서 $h[k]=0$인 시스템을 말한다.
이 시스템은 현재 시점보다 과거에 사용된 입력만을 사용하는 특징이 있다. 이 문구가 이해가 안될 수 있는데, 입출력 관계를 컨볼루션을 이용해 다시 써보자.
\[y[n]=\sum_{k=-\infty}^{\infty}h[k]x[n-k]\] \[=\sum_{k=-\infty}^{-1}h[k]x[n-k]+\sum_{k=0}^{\infty}h[k]x[n-k]\]위 식 중 아래의 식을 보면 첫 번째 항에는 $x[n+1]$, $x[n+2]$가 사용되고 두 번째 항에서는 $x[n]$, $x[n-1]$ 등이 사용되는 것을 알수 있다.
따라서, 이 시스템이 인과 시스템이라면 $x[n]$, $x[n-1]$ 등이 사용되기만 하므로 $h[n]=0 \text{ for } n \lt 0$이라면 과거의 입력만을 이용해 현재 출력이 계산되는 시스템이 되는 것이다.
안정 시스템과 불안정 시스템
시스템에서 안정, 불안정의 조건은 입력의 크기가 유한하고 출력의 크기도 유한한 경우를 의미한다.
실제 시스템에서는 출력으로 내보낼 수 있는 전압값이나 숫자의 크기가 한정되어 있기 때문에 무한히 발산하는 시스템을 만들 수는 없겠으나, 이론적으로는 무한한 크기로 발산하는 출력을 갖는 시스템을 불안정 시스템이라고 부른다.
영어로 Bounded Input Bounded Output이라고도 부르는데 줄여서 “BIBO 안정”이라고도 한다.
만약 입력 $x[n]$이 크기가 유한하여
\[|x[n]|\lt B_x\]라고 했을 때 출력 또한 유한한 크기를 갖게 하기 위해선 다음을 만족해야 한다.
\[|y[n]|=\left|\sum_{k=-\infty}^{\infty}h[k]x[n-k]\right|\leq\sum_{k=\infty}^{\infty}|h[k]||x[n-k]|\] \[\leq B_x\sum_{k=-\infty}^{\infty}|h[k]|\]따라서 유한한 출력을 갖기 위해선 임펄스 응답이 absolutely summable 해야 한다. 즉,
\[\sum_{k=-\infty}^{\infty}|h[k]|<\infty\]와 같은 조건을 가질 때 BIBO 안정 시스템이라고 할 수 있다.
유한/무한 길이의 임펄스 응답에 따른 구분
임펄스 응답의 길이가 유한하냐 무한하냐에 따라 Finite Impulse Response 시스템과 Infinite Impulse Response 시스템으로 구별하기도 한다.
사실 FIR/IIR 시스템의 구별은 나중에 필터를 설계할 때도 굉장히 중요한 위치를 차지한다.
가령 아래와 같은 시스템은 FIR 시스템이다.
\[y[n]=ax[n]+bx[n-1]\]이 때 임펄스 응답은
\[h[n]=a\delta[n]+b\delta[n-1]\]이다. 또, 아래와 같은 시스템은 IIR 시스템이다.
\[y[n]+ay[n-1]=b x[n]\]이 때 임펄스 응답은 다음과 같다.
\[h[n]=(-a)^nb\text{,}\ \ \ n\geq 0\]예제
문제 1.
아래와 같은 입출력 관계를 갖는 이동 평균 시스템에 대하여,
\[y[n]=\frac{1}{2}\left(x[n]+x[n-1]\right)\]1) 이 시스템이 LTI 시스템인지 판별하시오.
우선 선형성부터 판별해보자.
시스템을 $\mathcal{T}(\cdot)$이라고 이름 붙이도록 하자.
그러면, 아래가 성립한다면 선형 시스템이다.
\[\mathcal{T}(\alpha x_1[n]+\beta x_2[n])=\alpha\mathcal{T}(x_1[n])+\beta\mathcal{T}(x_2[n])\]좌변은 아래와 같고,
\[\mathcal{T}(\alpha x_1[n]+\beta x_2[n])=\frac{1}{2}\left\lbrace\alpha x_1[n]+\beta x_2[n] +\alpha x_1[n-1] + \beta x_2[n-1]\right\rbrace\]우변은 아래와 같다.
\[\alpha\mathcal{T}(x_1[n])+\beta\mathcal{T}(x_2[n]) = \alpha \left(\frac{1}{2}(x_1[n]+x_1[n-1]\right)+\beta \left(\frac{1}{2}(x_2[n]+x_2[n-1]\right)\]따라서, 좌변과 우변이 일치하므로 이 시스템은 선형 시스템이다.
이번엔 시불변성을 판별해보자. 아래가 성립한다면 시불변 시스템이다.
\[\mathcal{T}(x[n-k]) = y[n-k]\]여기서 좌변은 아래와 같다.
\[\mathcal{T}(x[n-k]) = \frac{1}{2}\left(x[n-k]+x[n-k-1]\right)\]또, 우변은 아래와 같으며 좌변과 동일하다.
\[y[n-k]=\frac{1}{2}\left(x[n-k]+x[n-k-1]\right)\]그러므로 이 시스템은 시불변 시스템이기도 하다.
정리하면 이 시스템은 선형 시불변 시스템이다.
2) 이 시스템의 임펄스 응답을 계산하시오.
임펄스 응답 $h[n]$은 입력이 $x[n]=\delta[n]$인 경우의 응답을 말한다. 따라서, 임펄스 응답은 아래와 같다.
\[h[n]=\frac{1}{2}(\delta[n]+\delta[n-1])=\begin{cases} 0.5 & n = 0, 1 \\ 0 & \text{otherwise} \end{cases}\]3) 특정 입력에 대한 출력을 계산하시오.
입력이 아래와 같다고 했을 때 출력을 계산하시오.
\[x[n]=\begin{cases} 1 & n = 0, 1, 2 \\ 0 & \text{otherwise} \end{cases}\]LTI 시스템에선 입출력 관계를 입력과 임펄스 응답의 컨볼루션으로 계산할 수 있다.
따라서 출력값은 다음과 같다.
\[y[n]=h[n] * x[n]\] \[=\sum_{k=-\infty}^\infty h[n-k]x[k]\]따라서, 모든 가능한 n에 대해 고민해보자면 $y[n]$은 다음과 같다.
$n=-1$일 때 $y[-1]=\cdots + x[-1]h[0]+x[0]h[-1]+x[1]h[-2]+x[2]h[-3]+\cdots = 0$
$n= 0$일 때 $y[0]=\cdots + x[-1]h[1]+x[0]h[0]+x[1]h[-1]+x[2]h[-2]+\cdots = 0.5$
$n= 1$일 때 $y[1]=\cdots + x[-1]h[2]+x[0]h[1]+x[1]h[0]+x[2]h[-1]+\cdots = 1$
$n= 2$일 때 $y[2]=\cdots + x[-1]h[3]+x[0]h[2]+x[1]h[1]+x[2]h[0]+\cdots = 1$
$n= 3$일 때 $y[3]=\cdots + x[-1]h[4]+x[0]h[3]+x[1]h[2]+x[2]h[1]+\cdots = 0.5$
$n= 4$일 때 $y[4]=\cdots + x[-1]h[5]+x[0]h[4]+x[1]h[3]+x[2]h[2]+\cdots = 0$
이 과정을 그림으로 표현하자면 다음과 같다.
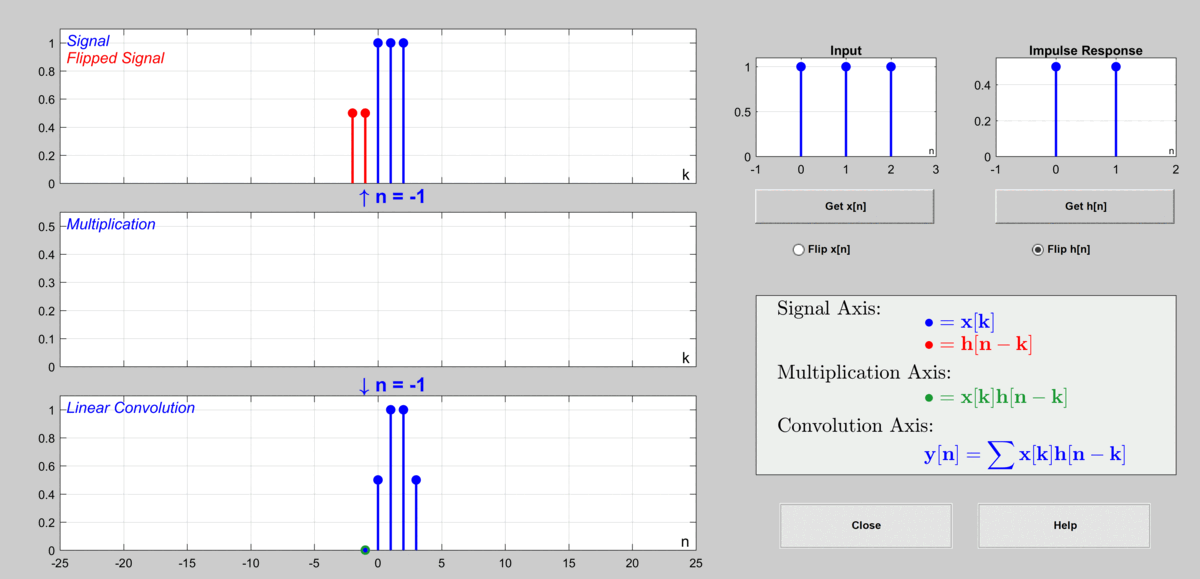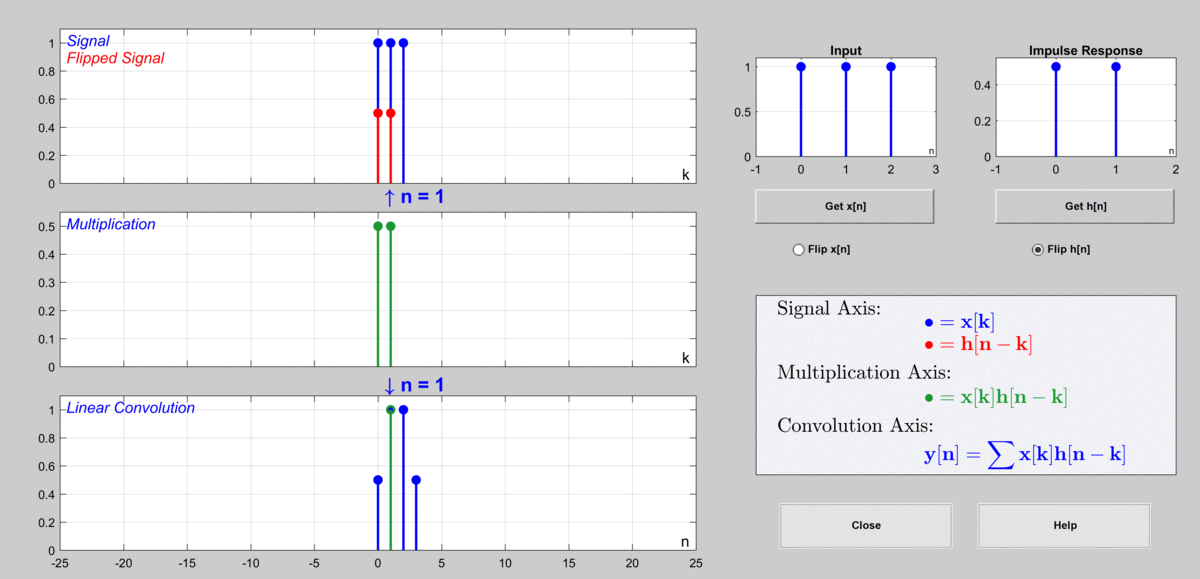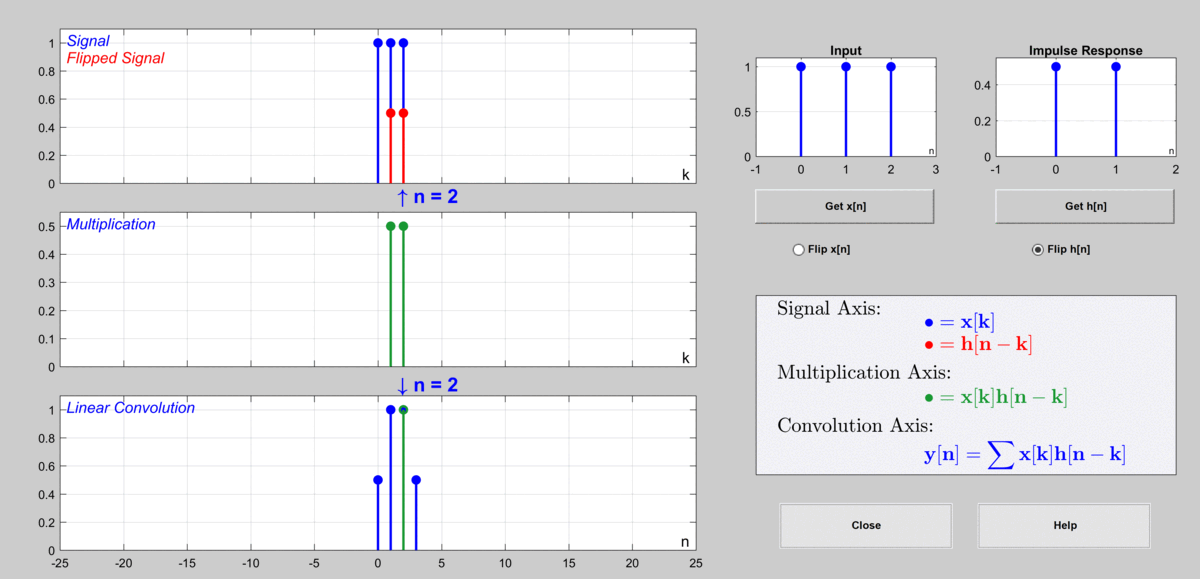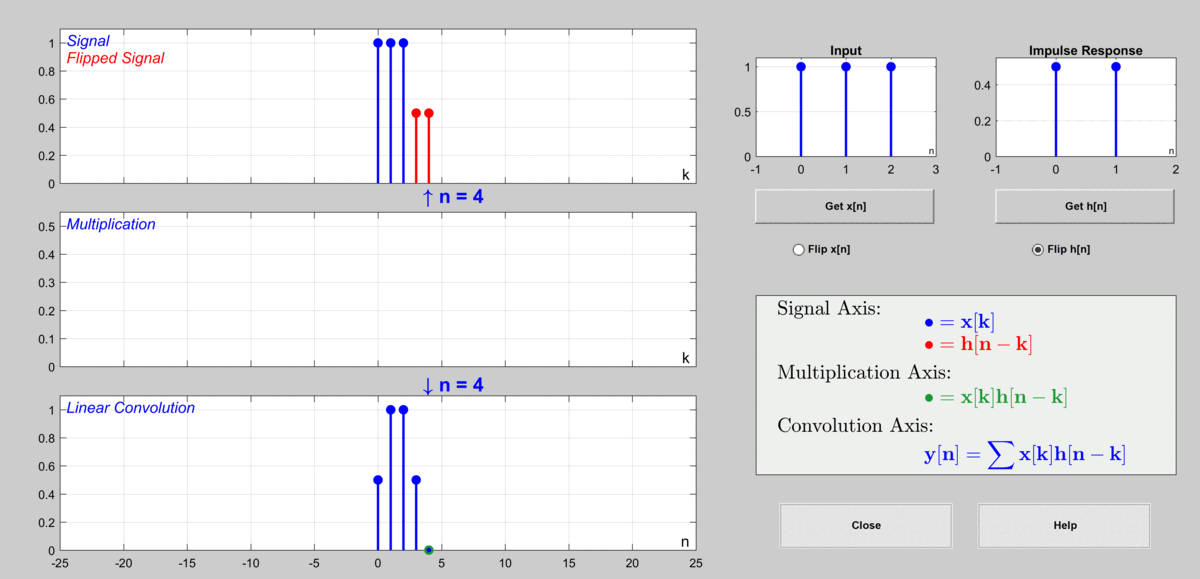
그림 9. 이산 컨볼루션을 통해 출력값을 계산하게 되는 과정
사용 GUI: DSP First의 MATLAB GUI 중 Discrete Convolution Demo
문제 2.
아래와 같은 입출력 관계를 갖는 자기 회귀 시스템에 대하여,
\[y[n] = a y[n-1] + b x[n]\]단, 아래의 조건이 만족된다고 가정한다.
\[x[n] = 0 \text{ for } n\lt 0\] \[y[n]=0 \text{ for }n=-\infty\]1) 이 시스템이 LTI 시스템인지 판별하시오.
이 시스템이 LTI 시스템인지 판별하기 위해선 시스템의 입출력 관계를 수정해서 표현해야 한다.
$y[-\infty]=0$이라는 조건에 의해 $n=-1$ 일 때, $y[-1]=0$ 이다.
그리고, $n = 0$일 때, $y[0]=b x[0]$ 이다. 이와 같은 방법으로 $n=1,2,\cdots$에 대하여,
\[y[1]=ab x[0]+b x[1]\] \[y[2] = a^2b x[0]+ab x[1] + b x[2]\] \[\vdots \notag\] \[y[n]=\sum_{k=0}^{n}a^k b x[n-k]\]이제 위 식을 이용해 선형성과 시불변성을 판별하자.
우선 선형성부터 판별해보자.
시스템을 $\mathcal{T}(\cdot)$이라고 이름 붙이도록 하자.
그러면, 아래가 성립한다면 선형 시스템이다.
\[\mathcal{T}(\alpha x_1[n]+\beta x_2[n])=\alpha\mathcal{T}(x_1[n])+\beta\mathcal{T}(x_2[n])\]좌변은 아래와 같고,
\[\mathcal{T}(\alpha x_1[n]+\beta x_2[n])=\alpha\left[\sum_{k=0}^{n}a^k b x_1[n-k]\right]+\beta\left[\sum_{k=0}^{n}a^k b x_2[n-k]\right]\]우변은 아래와 같다.
\[\alpha\mathcal{T}(x_1[n])+\beta\mathcal{T}(x_2[n]) = \sum_{k=0}^{n}a^k b\left[\alpha x_1[n-k]+\beta x_2[n-k]\right]\]따라서, 좌변과 우변이 일치하므로 이 시스템은 선형 시스템이다.
이번엔 시불변성을 판별해보자. 아래가 성립한다면 시불변 시스템이다.
\[\mathcal{T}(x[n-\tau]) = y[n-\tau]\]여기서 좌변은 아래와 같다.
\[\mathcal{T}(x[n-\tau]) = \sum_{k=0}^{n}a^k b x[n-\tau-k]\]그런데 summation notation 내의 $n-\tau+1$ 번째부터 $n$번째 값은 0과 같다.
왜냐면 각각의 $x[k]$ 값은 $x[n-\tau-(n-\tau+1)] = x[-1]$에서 $x[n-\tau-n]=x[-\tau]$에 해당하는데 $x[k] = 0\text{ for } k\lt 0 $이기 때문이다.
따라서 좌변의 식은 다음과 같이 고쳐쓸 수 있다.
\[\Rightarrow \sum_{k=0}^{n-\tau}a^k b x[n-\tau-k]\]또, 우변은 아래와 같으며 좌변과 동일하다.
\[y[n-\tau]=\sum_{k=0}^{n-\tau}a^k b x[n-\tau-k]\]그러므로 이 시스템은 시불변 시스템이기도 하다.
정리하면 이 시스템은 선형 시불변 시스템이다.
2) 이 시스템의 임펄스 응답을 구하시오.
위의 LTI 여부를 판별하기 위해 만든 입/출력의 관계에 따라,
\[y[n]=\sum_{k=0}^{n}a^k b x[n-k]\]이며 임펄스 응답은
\[h[n]=a^n b\]이다.
3) 특정 입력에 대한 출력을 계산하시오.
입력이 아래와 같다고 했을 때 출력을 계산하시오.
\[x[n]=\begin{cases} 1 & n = 0, 1, 2 \\ 0 & \text{otherwise} \end{cases}\]LTI 시스템에선 입출력 관계를 입력과 임펄스 응답의 컨볼루션으로 계산할 수 있다.
$n=0$ 인 경우 $y[0]=a^0 b x[0] = b$
$n=1$ 인 경우 $y[1]=\sum_{k=0}^{1}a^k b x[1-k] = a^0 b x[1-0] + a^1 b x[1-1] = b + ab$
$n=2$ 인 경우 $y[2]=\sum_{k=0}^{2}a^k b x[2-k] = a^0 b x[2-0] + a^1 b x[2-1] + a^2 b x[2-2] = b + ab+a^2b$
이와 같은 방법으로
\[y[n] = a^{(n-2)}b + a^{(n-1)}b+a^n b\]임을 알 수 있다.
아래 그림에서는 $a=0.8$, $b = 1$인 경우를 상정하였으며 임펄스 응답은 길이를 10개까지만 표시하였다.
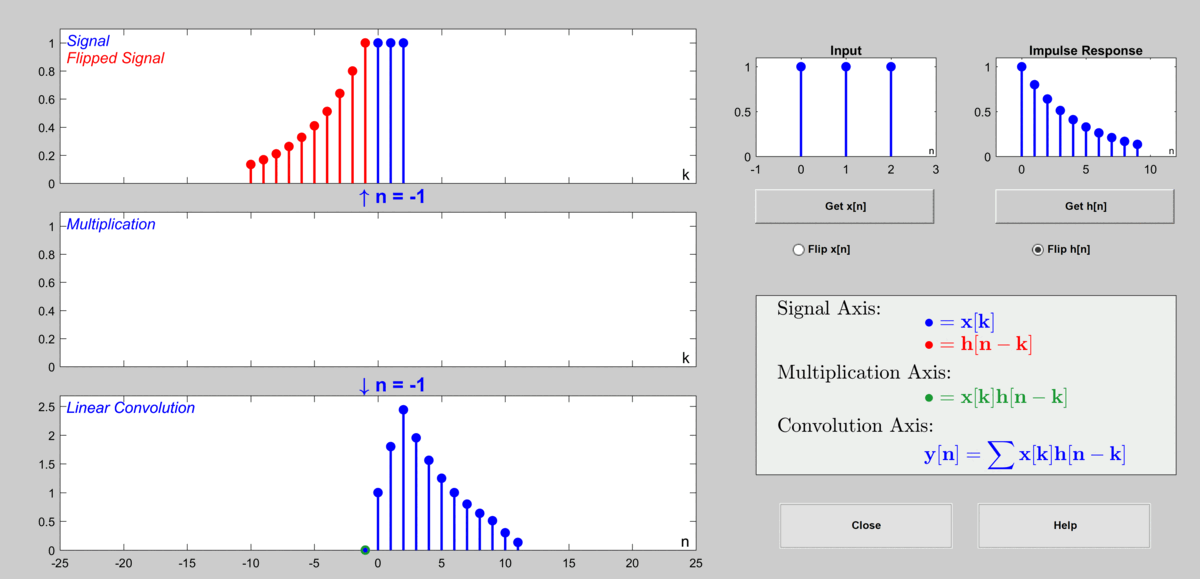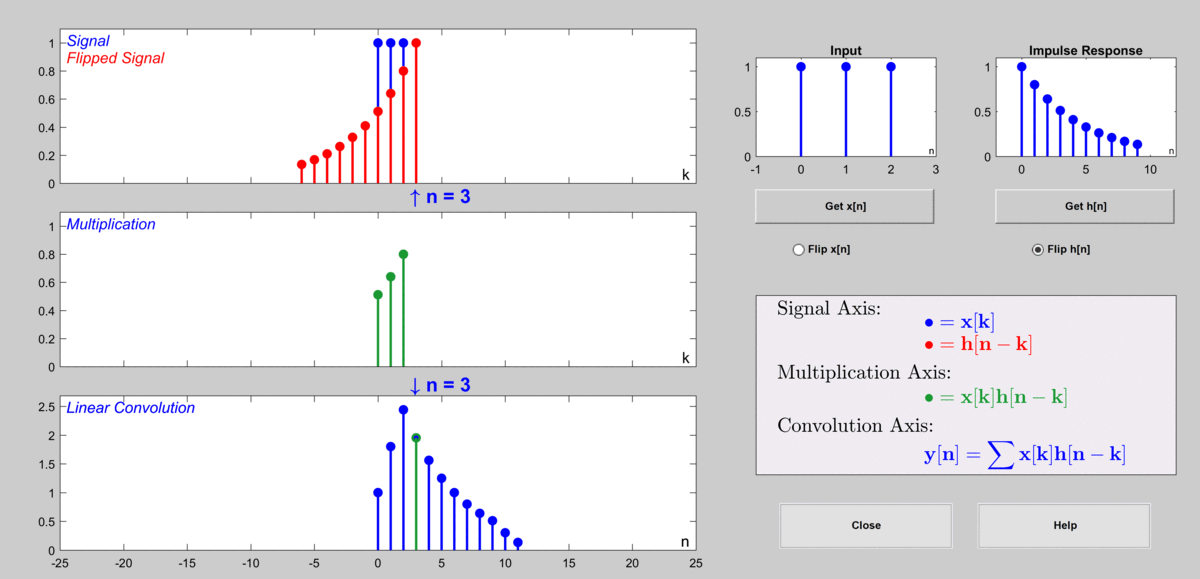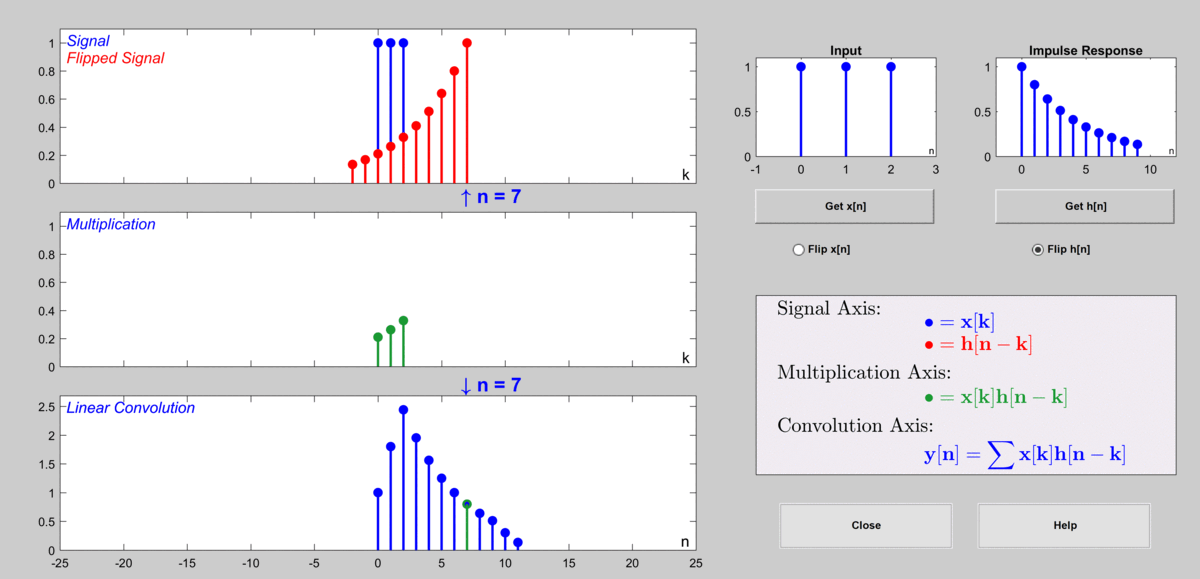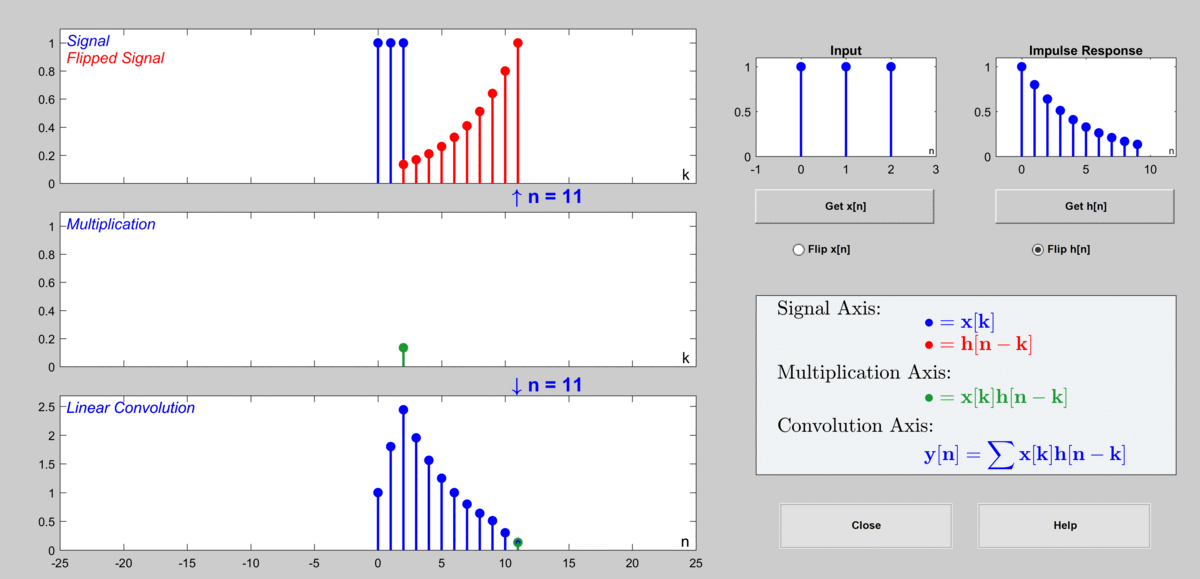
그림 10. 이산 컨볼루션을 통해 출력값을 계산하게 되는 과정
사용 GUI: DSP First의 MATLAB GUI 중 Discrete Convolution Demo
참고 문헌
- Hello! 신호 처리, James H. McClellan 등, 홍릉과학출판사
- 디지털 신호 처리, 이철희, 한빛아카데미