1. Random Process와 Fourier Transform

Continuous Time Fourier Transform(이하 CTFT)는 다음과 같이 정의된다.

$$G(\omega) = \int_{-\infty}^{\infty}g(t)\exp(-j\omega t)dt$$

where $\exp(-j\omega t) = \cos\omega t - j \sin \omega t$

이 때, Fourier Transform $G(\omega)$가 존재할 수 있는 조건은 Dirichlet Condition이라고 불리며, 그 조건은 다음과 같다.

1) $g(t)$ is absolutely integrable, that is,

$$\int_{-\infty}^{\infty}|g(t)|dt \lt \infty$$

2) $g(t)$ has only a finite number of discontinuouties in any finite interval

3) $g(t)$ has only finite number of maxima and minima within any finite interval

이 때, 우리가 궁금한 것은 왜 wide sense stationary 한 random process $X(t)$는 Fourier Transform이 될 수 없는지이다. 이 문제는 random process의 Fourier Transform은 왜 Dirichlet Condition을 만족할 수 없는지에 대한 문제로 귀결될 수 있다. 이 문제에 대한 핵심은 Dirichlet Condition 1번에 있다.

일반적으로 Stationary random process는 시간에 따라 random process $X(t)$의 pdf가 변하지 않는 것을 조건으로 하고 있다. 그 말은, random process $X(t)$의 realization 역시 시간 $t$에 따라 변하지 않는다는 것을 나타내며, $-\infty\lt x \lt \infty$에 대해서 $x(t)$는 언제나 유한한 값을 가질 수 있다는 것을 의미한다. 그러므로, Dirichlet condition 1은 위반 될 수 있으며, 일반적으로 random process $X(t)$의 Fourier Transform은 항상 존재하는 것은 아니다.

간단한 예를 들자면 다음과 같다. 다음과 같은 random process $X(t)$를 생각해보자.

random process $X(t)$의 random variable의 realization은 0 또는 1인데, $P(X=0) = 0.1$ 이고 $P(X=1) = 0.9$인 random variable이 있다고 하자.

그렇다면 random process 는 $-\infty\lt t \lt \infty$에 대해서 매우 낮은 확률로 $x(t) = 1 \text{ for }-\infty\lt t \lt \infty$일 수 있다. 그러면,

$$\int_{-\infty}^{\infty}1 dt = \infty$$

이다. 이렇듯 간단한 예를 통해서도 random process의 Fourier Transform이 항상 존재하는 것은 아니라는 사실을 알 수 있다.

2. Power Spectral Density of a WSS process

※ WSS: Wide Sense Stationary

그렇다면, 위와 같은 문제를 해결해줄 수 있는 가장 간단한 방법은 무엇일까?

그것은 random process $X(t)$의 $t$축에 boundary를 지정해주는 것이다. 즉,

$$X_T(t) = \begin{cases} X(t) && \text{ for }-T\lt t \lt T \\ 0 && \text{otherwise} \end{cases}$$

와 같이 $X_T(t)$를 놓고 생각해보는 것이다. 그 이후에, $T\rightarrow \infty$라고 만들면 Power Spectrum을 추정할 수 있게 되는 것이다. Power Spectral Density of a Wide Sense Stationary process의 증명과정은 다음과 같다.

$X_T(t)$의 푸리에 변환은 다음과 같을 것이다.

$$X_T(\omega) = \int_{-T}^{T}X_t(t)\exp(-j\omega t) dt$$

여기서 Parseval 정리를 이용해 신호의 energy를 정의해보자.

$$\int_{-T}^{T}X^2_T(t)dt = \frac{1}{2\pi}\int_{-\infty}^{\infty}|X_T(\omega)|^2 d\omega$$

또, 신호의 power는 신호의 energy에 신호 전체 길이를 나눠준 것이므로, 신호의 power는 다음과 같이 생각할 수 있다.

$$\frac{1}{2T}\int_{-T}^{T}X^2_T(t)dt = \frac{1}{2T}\frac{1}{2\pi}\int_{-\infty}^{\infty}|X_T(\omega)|^2 d\omega$$

그러면, power의 기댓값은 다음과 같다.

$$\frac{1}{2T}E\left\lbrace\int_{-T}^{T}X_T^2(t)dt\right\rbrace$$ $$=\frac{1}{2T}\frac{1}{2\pi}E\left\lbrace\int_{-\infty}^{\infty}|X_T(\omega)|^2 d\omega\right\rbrace$$ $$=\frac{1}{2\pi}E\left\lbrace\int_{-\infty}^{\infty}\frac{|X_T(\omega)|^2}{2T}d\omega\right\rbrace$$

여기서 $\frac{E\lbrace |X_T(\omega)|^2\rbrace}{2T}$는 주파수 $\omega$에서 파워의 기댓값에 기여한 기여도라고 볼 수 있으며, 이것이 $X_T(t)$의 Power Spectral Density(PSD)를 의미한다.

따라서 우리는 Power Spectral Density를 다음과 같이 정의할 수 있다.

$$S_{XX}(\omega) = \lim_{T\rightarrow \infty}\frac{E\lbrace |X_T(\omega)|^2\rbrace}{2T}$$

3. Autocorrelation과 Power Spectral Density의 관계

Autocorrelation과 PSD의 관계를 설명하는 이론은 Winer-Khinchin-Einstein 정리라고 불린다. 그 내용은 아래와 같으며 random process의 autocorrelation과 Power Spectral Density 간의 관계를 증명한다.

PSD의 식에서,

$$\frac{E \lbrace |X_T(\omega)|^2\rbrace}{2T}$$ $$=\frac{E \lbrace X_T(\omega)X_T^*(\omega)\rbrace}{2T}$$ $$=\frac{1}{2T}\int_{-T}^{T}\int_{-T}^{T}E\left\lbrace X_T(t_1) X_T(t_2) \exp(-j\omega t_1) \exp(-j\omega t_2) dt_1 dt_2\right\rbrace$$ $$=\frac{1}{2T}\int_{-T}^{T}\int_{-T}^{T}R_{XX}(t_1-t_2)\exp(-j\omega(t_1-t_2))dt_1 dt_2$$

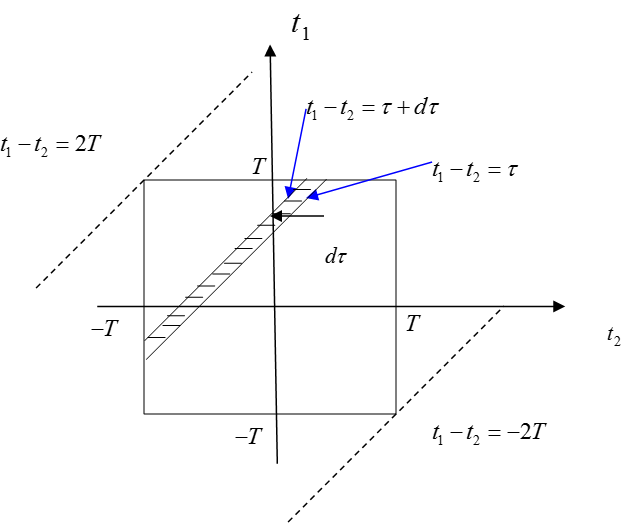
그림 1.

여기서 위의 식 (15)는 그림 1에서처럼 $t_1 = \pm T$와 $t_2 = \pm T$로 둘러싸인 정사각형 영역의 면적을 구하는 과정으로 볼 수 있다.

식 (15)를 보면 $t_1-t_2$라는 식이 일괄적으로 들어가있기 때문에, $t_1-t_2=\tau$와 같이 치환해서 적분식을 풀어줄 수 있다.

$t_1-t_2 = \tau$라는 식은 잘 생각해보면 기울기가 1인 일차함수 중 하나임을 알 수 있는데, 결국 그림 1의 정사각형을 구하는 과정을 $\tau$가 $-2T$부터 $2T$까지 변해가면서 그림 1에 shade 표시한 띠의 미소 면적을 적분해주는 과정이라고 볼 수 있는 것이다. 따라서, 그림 1에 shade 표시한 미소 면적을 $dA$라고 한다면 식 (15)는 다음과 같이 쓸 수 있다.

$$식(15)\Rightarrow \frac{1}{2T}\int_{-2T}^{2T}R_{XX}(\tau)\exp(-j\omega \tau) dA$$

여기서 $dA$를 구하면

$$dA = (2T-|\tau|)d\tau - \frac{1}{2}(d\tau)^2$$

이다. 이것은 두 삼각형의 넓이의 차를 이용해 구한 값이다.

따라서 식 (16)을 계속해서 쓰면,

$$\frac{E\lbrace X_T(\omega) X_T^*(\omega)\rbrace}{2T}$$ $$=\frac{1}{2T}\int_{-2T}^{2T}R_{XX}(\tau)\exp(-j\omega \tau)\left\lbrace(2T-|\tau|)d\tau - \frac{1}{2}d\tau^2\right\rbrace$$ $$=\frac{1}{2T}\int_{-2T}^{2T}R_{XX}(\tau)\exp(-j\omega \tau) \left\lbrace(2T-|\tau|) - \frac{1}{2}d\tau\right\rbrace d\tau$$ $$=\int_{-2T}^{2T}R_{XX}(\tau)\exp(-j\omega \tau) \left\lbrace \left(1-\frac{|\tau|}{2T}\right) -\frac{1}{4T}d\tau \right\rbrace d\tau$$

여기서 $R_{XX}$가 적분가능하다면, $T$가 무한히 커지게 되면 식 (21)은 아래와 같다.

$$\int_{-\infty}^{\infty}R_{XX}(\tau) \exp(-j\omega\tau)d\tau$$

따라서 아래와 같은 관계를 확인할 수 있다.

$$\lim_{T\rightarrow \infty}\frac{E\lbrace |X_T(\omega)|^2\rbrace}{2T} = \int_{-\infty}^{\infty}R_{XX}(\tau)\exp(-j\omega \tau)d\tau$$

앞서 언급했듯이 위 식의 좌변은 Power Spectral Density $S_{XX}(\omega)$라고 부른다. 따라서,

$$S_{XX}(\omega) = \int_{-\infty}^{\infty}R_{XX}(\tau)\exp(-j\omega \tau)d\tau$$

그리고, 역푸리에 변환을 이용하면

$$R_{XX}(\tau) = \frac{1}{2\pi}\int_{-\infty}^{\infty}S_{XX}(\omega)\exp(j\omega\tau)d\omega$$

임 또한 생각해볼 수 있다.