지금까지 우리는 벡터란 무엇인지에 대해 알아보고, 행렬과 벡터의 곱에 대해 알아보았다.
짧게 요약하자면 벡터란 상수배(곱셈 규칙)와 덧셈 규칙이 정의되는 원소들이라고 하였으며, 이들의 집합에 이 연산들이 정의된 집합을 벡터 공간(vector space)라고 한다고 하였다. 여기서 이러한 상수배와 덧셈 규칙이 정의되는 원소들을 ‘선형성을 갖는다’라고 표현한다.
또, 행렬은 벡터를 또 다른 벡터로 변환 시키는 일종의 연산자로 볼 수 있으며, 특히 행렬과 벡터의 곱은 행렬의 열벡터들을 얼마나 선형결합 시킬 것인가라는 의미로 볼 수 있다고 하였다.
이번 시간에는 행벡터의 기능과 역할에 대해 알아보고, 이를 통해 벡터의 내적이 왜 기하학적으로 한 벡터에서 다른 벡터로의 정사영과 관련이 되어 있는지를 알아보고자 한다.
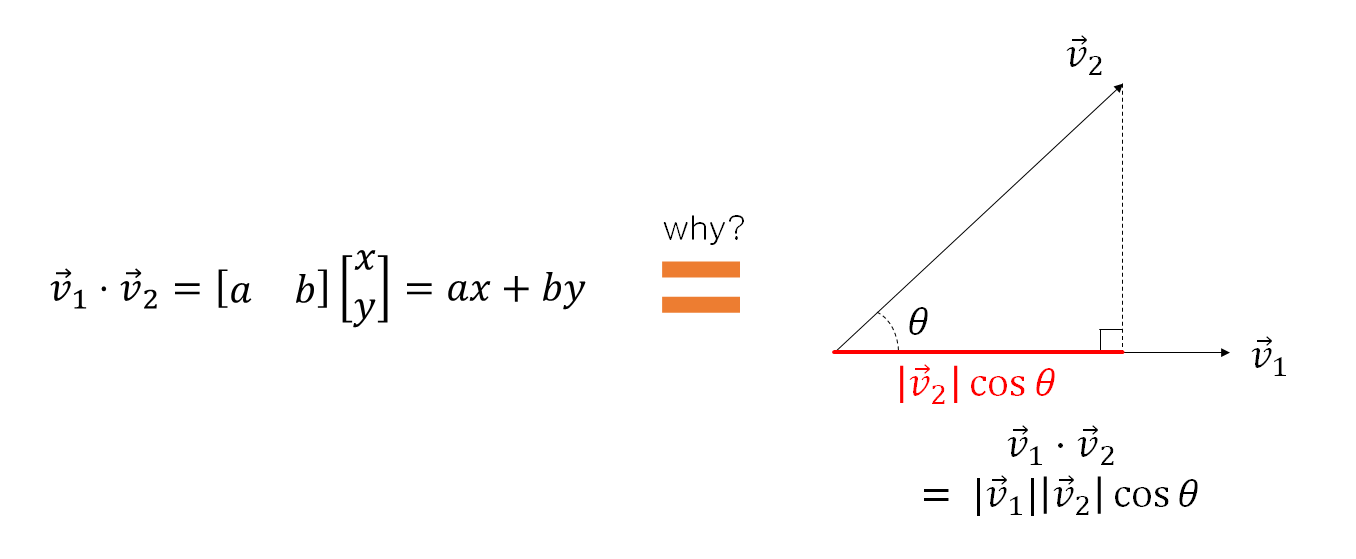
그림 1. 행벡터의 기능과 역할은 무엇이며 이것이 벡터의 내적의 기하학적 의미와는 어떻게 연관되어 있을까?
행벡터의 기능과 역할
행렬과 행렬의 곱 혹은 행렬과 벡터의 곱에 대해 생각해보면 행렬의 곱을 해석할 수 있는 가장 기본적인 방법은 아래와 같이 곱해지는 행렬 중 왼쪽 행렬의 행 요소들과 오른쪽 행렬의 열 요소들의 값들을 순서대로 곱해주고 더해주는 방법이다.
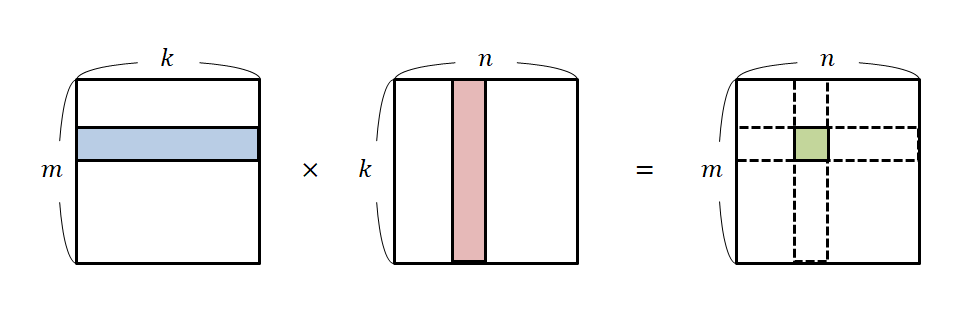
그림 2. 행렬의 곱에 관한 가장 기본적인 해석
이것은 행렬의 곱에 대한 새로운 이해편에서 이러한 해석이 행벡터와 역벡터 간의 내적으로 해석될 수 있다고 언급하였다. 하지만, 이번에는 ‘내적’이라는 용어나 계산 방법을 모른다고 생각하고, 오직 행렬의 곱셈만이 주어진 상태라고 했을 때 행벡터와 열벡터 간에 어떤 일이 일어나는지 알아보도록 하자.
우리는 보통 ‘벡터’라 하면 열벡터를 우리가 “흔히 말하는” 벡터라고 본다. 이것은 일종의 수학적 관례로써 기준을 잡아둔 것으로 생각하면 된다. 다시 말해, 변화가 되는 대상을 열 벡터로 보자고 관례적으로 잡아둔 것이다.
반면, 행벡터는 열벡터에 대한 함수이다. 무슨 말이냐 하면, 방금 언급했듯 열벡터는 ‘변화의 대상’이 되는 것에 반해 행벡터는 변화를 시키는 행위자인 것이다.
가령 $[2, 1]$이라는 행벡터와 $[3, -4]^T$라는 열벡터에 대해 다음과 같은 곱셈을 생각해보자.
\[\begin{bmatrix}2 & 1\end{bmatrix}\begin{bmatrix}3\\-4\end{bmatrix} = 2\cdot 3 + 1\cdot(-4) = 6-4 = 2\]이것을 달리 생각해보면 아래와 같이 함수의 표기로 생각할 수도 있다.
\[\begin{bmatrix}2 & 1\end{bmatrix}\left(\begin{bmatrix}3\\-4\end{bmatrix}\right) = 2\]즉, 행벡터는 열벡터를 입력으로 받아 스칼라를 출력하는 $f:V\rightarrow\Bbb{R}$인 함수1인 것이다.
행벡터의 시각화
지금까지 우리는 행벡터는 열벡터를 입력으로 받는 함수라고 언급하였다. 그러면 우리는 함수로써의 행벡터를 시각화 할 수 있을까?
함수를 시각화 한다는 것의 의미는 임의의 입력 $x$에 대해 함수의 출력 $f(x)$를 대응시킨 좌표들을 나열한 것이다.
가령 $y=x^2$을 시각화 한다는 것은 시각화하기에 좋은 범위의 $x$, 가령 $-2\leq x \leq 2$ 에 대해 대응되는 $y=f(x)=x^2$ 값을 좌표 평면에 모두 나타낸 것이다.
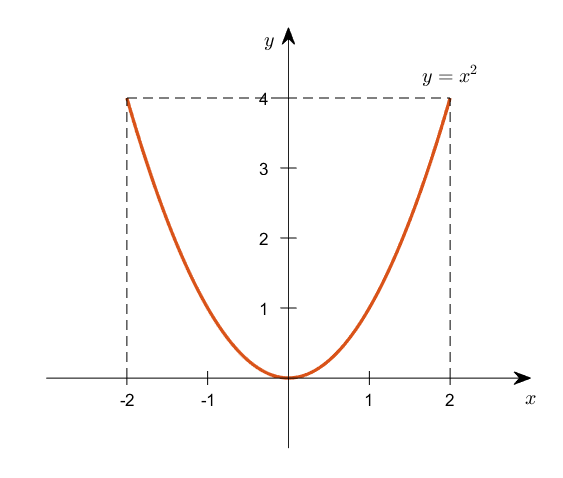
그림 3. 함수 $y=x^2$을 $-2\leq x \leq 2$ 의 범위에 대해 시각화 한 것
그렇다면 $\begin{bmatrix}2 & 1\end{bmatrix}$이라는 행벡터를 시각화 한다고 하면, 임의의 벡터 $\begin{bmatrix}x & y \end{bmatrix}^T$에 대해 함수의 출력을 좌표계에 나열하면 된다.
\[\begin{bmatrix}2 & 1 \end{bmatrix}\left(\begin{bmatrix}x \\ y \end{bmatrix}\right) = 2x+ y\]행벡터는 열벡터를 입력으로 받고 스칼라값을 출력하므로 여러가지 출력에 대한 함수를 하나의 $x, y$ 평면에 나타낼 수도 있을 것이다.
가령, $2x+y=1$을 만족하는 $x, y$ 쌍을 나타내면 $y=-2x+1$이라는 선 위에 모두 표시할 수 있을 것이다.
이렇듯 여러 스칼라 출력값에 대한 결과를 한번에 표시하기 위해서 등고선의 아이디어를 차용해보자.
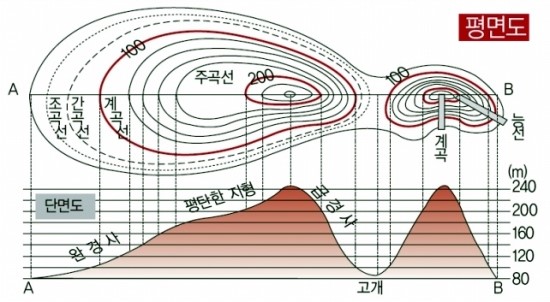
그림 4. 등고선의 예시. 등고선은 같은 높이를 갖는 위치들을 곡선으로 이어 연결한 것이다.
그림 출처
등고선은 그 이름에서 알 수 있듯이 높이가 같은 곳들을 하나의 선으로 연결한 지도를 의미한다. 우리는 여기서 동일한 스칼라 출력값을 갖는 $x, y$ 순서 쌍들을 하나의 선으로 연결하도록 하자.
즉, 이 등고선을 이용하면 임의의 벡터 $\vec{v}$가 $\begin{bmatrix} 2 & 1\end{bmatrix}$이라는 함수를 통과했을 때의 출력값을 쉽게 시각화 할 수 있게 된다.
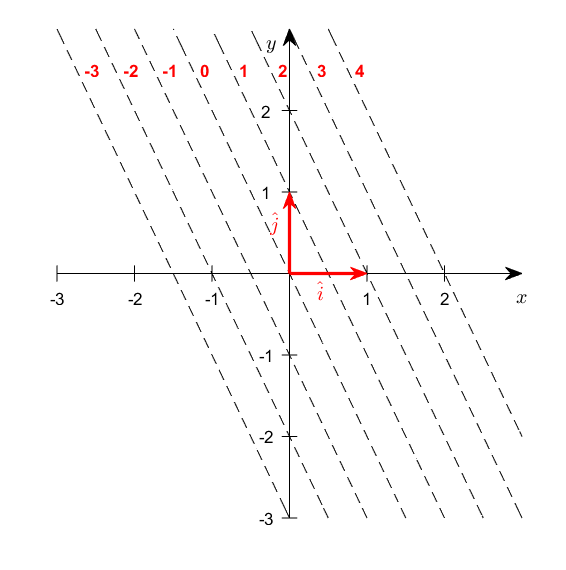
그림 5. 행벡터를 통해 출력된 함수값들의 시각화
그림 5를 보면 $2x+y$의 출력값이 각각 -3부터 4에 해당되는 $x, y$ 순서 쌍들을 한 선에 표시한 것을 알 수 있다.
여기서 이 순서쌍들 중 일부를 화살표 모양의 벡터 형태로 표시하면 아래의 그림 6에서 볼 수 있는 것들과 같다.
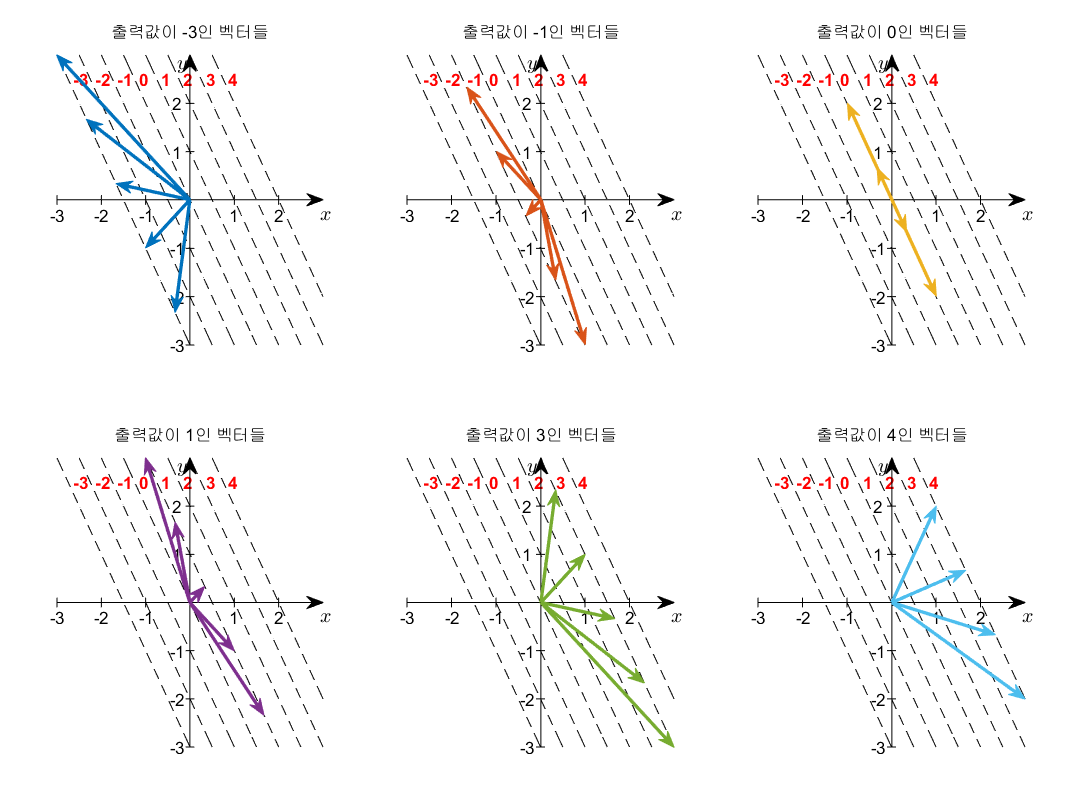
그림 6. 함수로써의 행벡터의 다양한 출력값에 대해, 각각의 출력값이 나오게 하는 입력 열벡터들의 예시.
가령, 그림 6의 가장 좌상단에서 볼 수 있는 출력값이 -3인 벡터들을 보면 모두 $2x+y=-3$인 점선 위에서 종점(end point)을 가지는 벡터들의 집합인 것을 알 수 있다.
행벡터와 벡터의 내적
그렇다면 이쯤해서 벡터 간의 내적의 기하학적 의미에 대해 생각해보도록 하자.
우리는 그림 1의 오른쪽에서 볼 수 있듯이 임의의 두 벡터 $\vec{v}_1$과 $\vec{v}_2$에 대해 두 벡터의 사잇각이 $\theta$라면 벡터의 내적은 다음과 같이 계산된다는 것을 알고있다.
\[\vec{v}_1\cdot\vec{v}_2 = |\vec{v}_1||\vec{v}_2|\cos\theta\]여기서 $|\vec{v}_2|\cos\theta$는 $\vec{v}_2$의 $\vec{v}_1$방향으로의 정사영이라는 점도 알 수 있을 것이다.
우리는 그림 6의 여러 subplot 중에서 출력 스칼라 값이 4가 되게 하는 경우에 대해 생각해보자. 이 때, 출력 스칼라 값이 4가 되게하는 임의의 벡터를 하나 생각해 그려보면 다음과 같다.
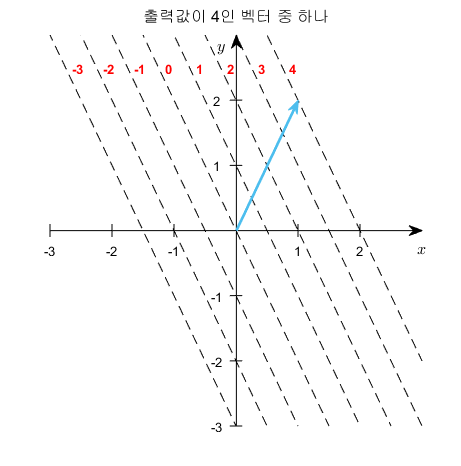
그림 7. 출력 스칼라 값이 4가 되게 하는 임의의 벡터 하나를 생각해보자.
여기서 출력 스칼라 값이 4라는 것은 어떤 의미일까? 우리는 행벡터에 해당하는 $[2, 1]$을 그려본 뒤, $2x+y=4$라는 점까지의 거리를 생각해보자.
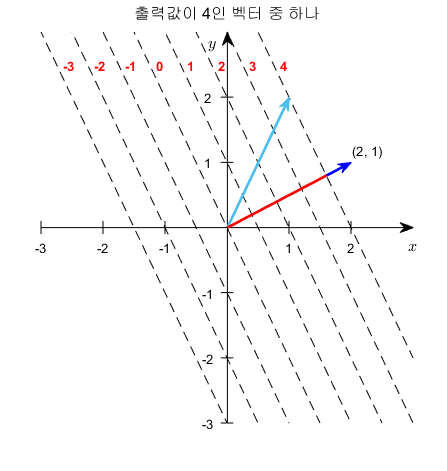
그림 8. 행벡터 $[2, 1]$(진한 파란색)과 $2x+y=4$까지의 거리(빨간색)
생각해보면 $2x+y=c$에 해당하는 점선은 모두 행벡터 $[2, 1]$에 수직이다. 왜냐면 행벡터가 점선으로 표현한 함수들에 대한 법선 벡터 역할을 하기 때문이다.
따라서, 그림 8에서 빨간색으로 표현한 길이는 다음과 같이 직각 삼각형의 높이를 계산함으로써 얻을 수 있다.
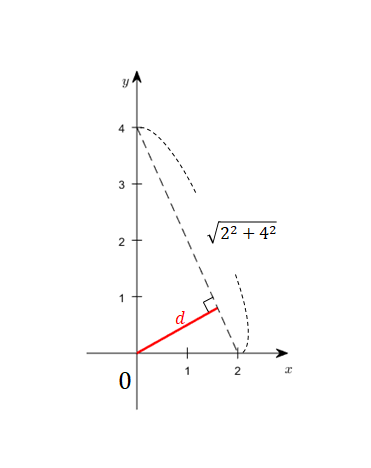
그림 9. 직각 삼각형의 넓이를 구하는 방법을 이용해 $d$의 길이를 계산할 수 있다.
즉,
\[4\times 2 = d\times \sqrt{20}\]이므로,
\[d= \frac{8}{\sqrt{20}}=\frac{4}{\sqrt{5}}\]이다.
여기서 행벡터 $[2, 1]$의 길이는 $\sqrt{5}$인데, 이 길이를 $d$에 곱하면
\[d\times\sqrt{5} = \frac{4}{\sqrt{5}} * \sqrt{5} = 4\]임을 알 수 있다.
즉, 열벡터의 정사영 길이 * 행벡터의 길이 = 내적 값과 일치함을 알 수 있다.
사실 그림 7에서 볼 수 있듯이 벡터의 내적을 계산할 때에는 $2x+y=4$의 점선 위에 있는 어떤 벡터를 고르더라도 행벡터 $[2, 1]$ 과의 내적 계산은 4가 되는 것을 알 수 있고,
이것은 다시 말해 열벡터의 정사영 길이가 내적 계산에 이용되기 때문임을 기하학적으로 확인할 수 있는 것이다.
행벡터와 행공간
행벡터도 열벡터와 마찬가지로 벡터의 정의를 만족하며 선형성을 갖는다. 따라서 행벡터도 일반적인 벡터로 생각할 수 있는 것이다.
그런데 이러한 선형성을 만족하는지 알아보는 것이 왜 중요할까? 그것은 행벡터가 처리 대상인 ‘데이터’가 아니라 ‘함수’임에도 선형성을 갖는다면 일반적인 벡터에 적용할 수 있다고 알려진 모든 method들을 적용할 수 있기 때문이다.
우선은 행벡터는 아래와 같이 벡터 합의 연산이 성립한다.
함수로써의 행벡터를 함수 $f$로 표현하고, 임의의 두 열벡터 $\vec{v}$와 $\vec{w}$에 대해 아래가 성립한다.
\[f(\vec{v}+\vec{w}) = f(\vec{v}) + f(\vec{w})\]예를 들면, 아래의 좌변과 우변의 결과는 같다는 것을 쉽게 알 수 있다.
\[\begin{bmatrix}2 & 1\end{bmatrix}\left(\begin{bmatrix}3\\-4\end{bmatrix} + \begin{bmatrix}1\\2\end{bmatrix}\right) = \begin{bmatrix}2 & 1\end{bmatrix}\left(\begin{bmatrix}3\\-4\end{bmatrix}\right) + \begin{bmatrix}2 & 1\end{bmatrix}\left(\begin{bmatrix}1\\2\end{bmatrix}\right)\]또, 상수배 연산이 성립한다.
임의의 스칼라 $n$에 대해 다음이 성립한다.
\[f(n\vec{w}) = nf(\vec{w})\]예를 들면, 아래의 좌변과 우변의 결과가 같다는 것을 쉽게 알 수 있다.
\[\begin{bmatrix}2 & 1\end{bmatrix}\left(2\begin{bmatrix}3 \\ -4\end{bmatrix}\right) = 2\begin{bmatrix}2 & 1\end{bmatrix}\left(\begin{bmatrix}3 \\ -4\end{bmatrix}\right)\]정리하자면 행벡터는 다음과 같은 기능과 성질을 갖는다.
- 열벡터를 입력으로 받아 스칼라(즉, 숫자)를 출력하는 함수
- 또, 행벡터는 선형연산자이다.
- 다시 말해 두 벡터를 더한 채로 함수 출력을 볼 때와 두 벡터의 함수 출력을 합한 것이 같음.
- 또 다시 말해, 선형연산자이기 때문에 입력에 상수배를 해준 채로 함수를 출력할 때와 출력된 함수에 상수배를 해준 것의 결과는 같음.
행벡터가 선형함수라는 것의 기하학적 의미.
행벡터의 스칼라배
우리는 그림 6에서와 같이 행벡터에 열벡터를 입력시켰을 때 얻는 스칼라 출력값을 등고선을 이용해 표현해보았다.
이 그림을 다시 생각해보면 주어진 행벡터에 대해서 어떤 열벡터와의 연산 후 출력된 스칼라 값을 생각하는 방법은 해당 열벡터가 등고선 몇 개를 통과했는가와 같다고도 볼 수 있다.
따라서, 행벡터의 길이가 길어진다면 등고선의 간격이 더 좁아지는 것과 같은 효과를 내게 된다는 것을 알 수 있다.
반대로 행벡터의 길이가 짧아진다면 등고선의 간격이 더 넓어지는 것과 같은 효과를 내게 된다는 것 또한 알 수 있다.
그림 10. 다양한 스칼라배로 크기가 커지거나 작아지는 행백터에 대응한 시각화
행벡터 간의 합
또한, 행벡터 간의 합이 의미하는 것은 두 개의 서로 다른 등고선이 합해져서 새로운 등고선을 만들어낼 수 있음을 의미한다.
이 때, 새롭게 만들어지는 등고선은 두 개의 서로 다른 등고선이 표방하는 행벡터들이 합쳐져 얻어진 새로운 행벡터에 수직하도록 형성된다.
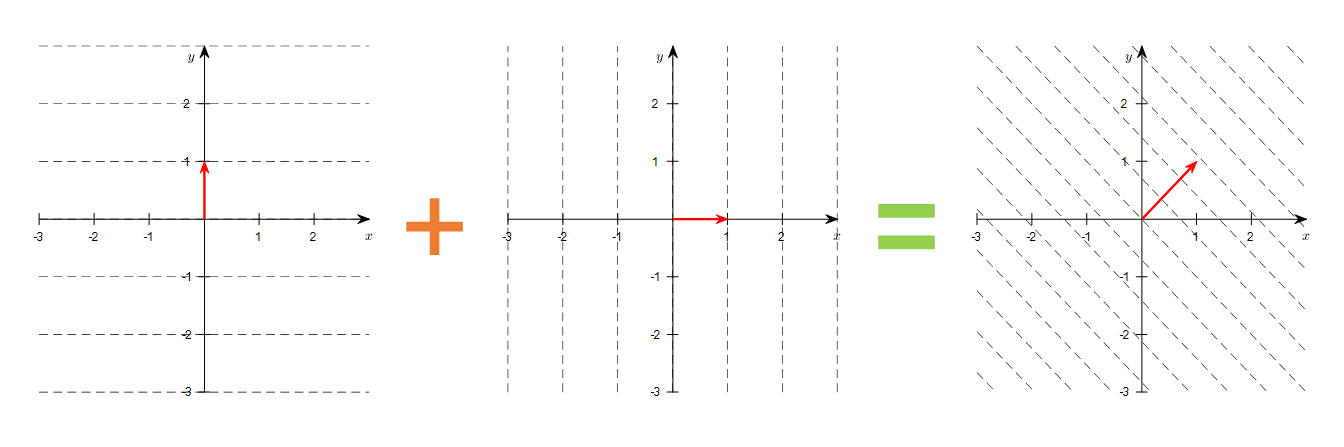
그림 11. 두 행벡터를 더해서 얻게되는 새로운 행벡터에 대응되는 등고선 시각화
행공간은 열공간의 쌍대공간
벡터에 대해 정의할 때 스칼라배와 벡터 간의 합에 대해 정의가 되는 것들을 벡터로 정의한다고 하였으며, 이 벡터는 벡터 공간을 이룬다고 하였다.
따라서, 행벡터에 대한 선형 함수1로 생각할 수 있는 행벡터들도 일반적인 벡터로 간주할 수 있다는 것을 알 수 있다.
이 때, 덧셈 법칙과 곱셈 법칙이 정의된 행벡터들로 구성된 집합을 행공간이라고 부른다.
지금까지 우리가 행벡터를 행벡터라고 불렀기 때문에 당연히 벡터라고 생각하고 있지만, 이렇듯 엄밀한 잣대를 들이댐으로써 새로운 개념의 벡터에 대해 생각해볼 수 있는 것이다.
행공간은 열공간에 대응되는 공간이라는 의미에서 쌍대공간(dual space)이라고 불리며, dual space의 엄밀한 정의는 다음과 같다.
| DEFINITION Dual Space |
|---|
| Vector Space $V$의 선형 범함수들의 집합 $$V^*=\left\lbrace f:V\rightarrow \Bbb{R} | f(c\vec{a}+\vec{b})\text{ for all }\vec{a},\vec{b}\in V\right\rbrace$$ 을 $V$의 dual space라고 한다. |
쌍대 공간의 개념이 중요한 것은 원래의 벡터 공간에서 특정 문제를 풀기가 어려운 경우에 해당 쌍대 공간에서는 문제가 쉽게 풀리는 경우가 있기 때문이다.
가령, 선형회귀에 대한 선형대수학적 해석이나 푸리에 변환에서 시간-주파수 간의 변환은 모두 쌍대성의 개념을 이용한 것이다.