0. prerequisites

우선 phasor에 대해 정확히 이해하기 위해선 다음의 개인정리를 꼭 읽기 바람. 또는 아래의 내용에 대해 알고 있는 사람이라면 계속 공부하셔도 무방합니다.

• 허수란 무엇인가?
• 자연상수 e의 의미
• 오일러 공식의 유도과정과 그 의미

1. 정현파란 무엇인가?

푸리에 분석의 최종적 결론이라고 할 수 있는 모든 신호는 정현파의 합으로 나타낼 수 있다는말은 학부시절 귀 따갑게 들었던 말이다 (독자가 현재 학부 과정 중에 있다면 귀에 따갑게 듣게 될 것이다.). 이 말은 굉장히 중요한 의미를 갖는데 그 중에서도 신호 분석에 있어서 phasor 분석이 가능하게 되는 시발점을 제공해준다. 즉, 정현파만의 어떠한 분석적인 특성이 phasor라는 특별한 신호 분석 방법을 제공해준다는 것이다. 그렇다면 정현파란 무엇일까? 모든 정현파(sinusoidal wave)는 막대기의 회전 운동으로부터 유도된다는 사실을 잊어선 안될 것이다. 막대기의 회전 운동에 대해 생각해보자.

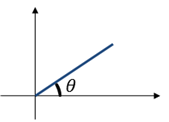
그림 1. x축과의 각도가 $\theta$인 막대기

그림 1과 같은 막대기가 있다고 하자. x축과 $\theta$라는 각도를 가지고 원점을 중심으로 막대기가 기울어져 있다. 이 때 우리는 원점을 중심으로 막대기가 회전한다고 상상하자. 이 때, 막대기의 위에서 아래로 비친 그림자의 궤적을 추적한 것을 cosine이라고 한다. 중학교 시간에 배운 내용이다.

그렇다면 sine이란 무엇인가? sine은 오른쪽에서 왼쪽으로 빛을 비추었을 때 나오는 그림자의 궤적을 추적한 것이라고 배웠지만, 어떻게 생각하면 sine과 cosine은 막대기의 시작점만 다른 것일 뿐이다. 즉, 막대기를 회전 시킬 때 90도 더 뒤로 당겨서 회전시키면 sine 파의 파형을 얻을 수 잇다. 그림 2의 오른쪽 부분을 보면 더 잘 알 수 있다.

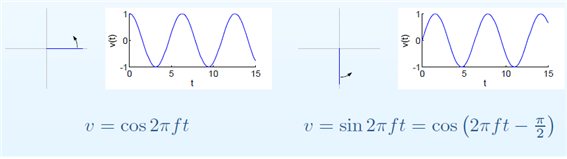
그림 2. cosine파와 sine 파는 막대기의 회전 시작 위치만 다를 뿐 사실상 같은 '원의 회전'에 관한 기술(description)이다.

즉, 여기서 말하고자 하는 것은 sine이나 cosine이나 모두 cosine으로 환원해서 생각할 수 있다는 것이다. phasor 분석에서 중요한 전제는 모든 정현파를 cosine으로 환원해서 생각하는 것으로부터 출발하자는 것이다. 그래야만 위상의 기준점을 설정할 수 있기 때문이다. 다시 말하자면, sine은 막대기의 각도가 $-\pi/2$만큼 이동한 곳에서 막대기가 회전을 시작할 때, 위에서 아래로 빛을 비추어서 얻어낸 그림자의 궤적과 같다라고 할 수 있겠다.

이제 조금 더 수학적으로 막대기를 분석해보도록 하자.

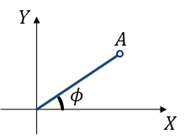
그림 3. 길이가 $A$이고 x 축과의 각도가 $\phi$인 막대기

그림 3에서 볼 수 있듯이 막대기의 길이가 A이고, 회전을 시작하는 맨 처음의 각도가 $\phi$라고 해보자.

그렇다면, 이 때 주파수 $f$로 막대기가 반시계방향 회전을 한다고 하자. 그러면 위에서 아래로 빛을 비추어 얻어낸 그림자의 궤적을 따라 값을 표현한다면 다음과 같이 표현할 수 있겠다.

\[A \cos(2\pi f t + \phi)\] \[= A \cos(\phi) \cos(2\pi f t)-A \sin(\phi)\sin(2\pi f t)\] \[= X \cos(2\pi f t)- Y\sin(2\pi f t)\]

즉, 주파수 성분은 고정되어 있다고 하면 $A\cos(2\pi f t + \phi)$ 를 코사인 공식을 이용해서 (2)와 같이 분해할 수 있게 되고, (3)에서 볼 수 있는 것 처럼 점 A의 좌표 $(X,Y)=(A \cos (\phi) , A\sin(\phi))$ 를 얻어낼 수 있게 된다. phasor 분석의 핵심 아이디어는 바로

주파수 성분은 고정되어 있다고 하면, X와 Y의 값만을 가지고 막대기의 길이 $A$, 시작 각도 $\phi$인 막대기의 회전운동을 나타낼 수 있기에 충분하다

는 것이다. 그러므로, 우리는 $(X,Y)=(A\cos(\phi), A\sin(\phi))$ 라는 벡터를 생각할 수 있게 되고, 이 2차원 벡터 하나만 가지고도 회전 운동을 표현할 수 있게 되는 것이다.

그런데, 이 2차원 벡터를 표현해주는 좌표계를 phasor에서는 복소평면으로 책정했다. 그 이유는 허수는 회전을 의미하기 때문이다 ¹.

따라서 벡터

\[(X,Y) = (A\cos(\phi), A\sin(\phi))\]

는 다음과 같이 표현할 수 있다.

\[(X,Y) = X+jY = A\cos(\phi) + jA\sin(\phi)\]

또 이것을 오일러 공식을 활용하면 다음과 같이 표현할 수도 있다.²

\[A\times exp(j\phi)\]

또는 간단하게 막대기의 길이 와 각도 만을 가지고 다음과 같이 표현할 수도 있다.

\[A\angle\phi\]

그러므로, 네 가지 방법을 이용해 하나의 회전운동하는 막대기를 표현할 수 있게 되며, 주파수가 고정되어 있다고 가정한다면 네 개의 표현 방법은 모두 같은 현상을 표현한 것이다. 이 중 복소수 표기법과 phasor notation 표기법이 자주 쓰인다. phasor는 시간함수로 표현되는 것을 복소수 표기법으로 나타낸 것 또는 polar coordinate representation으로 표현된 것을 통틀어 phasor라고 부른다.

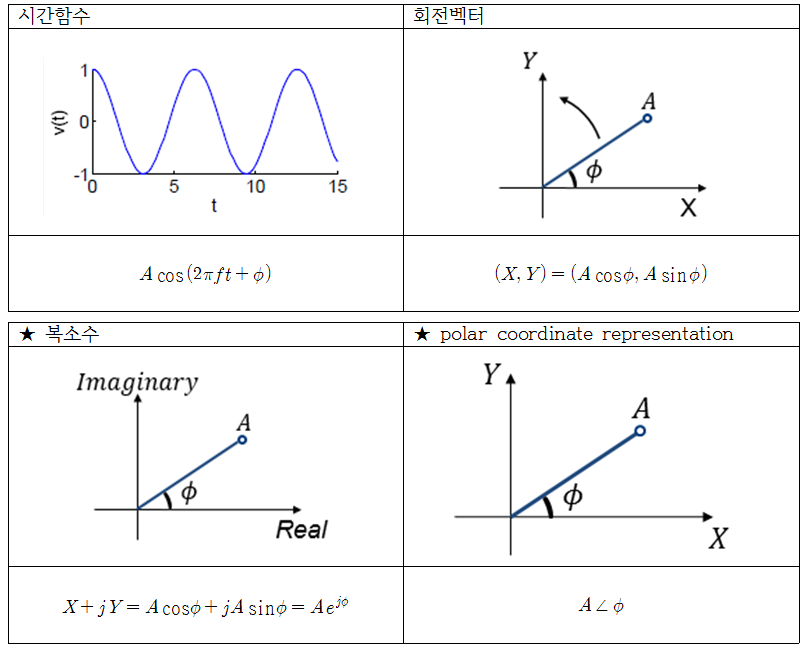
그림 4. 정현파를 표현할 수 있는 네 가지 방법.

2. phasor의 예제 문제

phasor의 표현 방법에 대해 알아보았으니 간단한 예제를 풀어보도록 하자. 모든 예제에서 주파수는 고정되어 있다고 가정한다. 즉, $f$ 는 상수임.

예1) $v(t)=\cos(2\pi ft)$ 을 복소수 표현방법과 polar coordinate representation으로 표기하시오.

정답: 복소수 표현방법으로 표기하자면 $V=1$ 이고, polar coordinate representation으로 표기하면 $1\angle 0°$ 이다.

예2) $v(t)=\sin(2\pi ft)$ 를 복소수 표현방법과 polar coordinate representation으로 표기하시오.

정답: 복소수 표현방법으로 표기하자면 $V=-j$ 이고, polar coordinate representation으로 표기하면 $1\angle -90°$ 이다.

예3) $v(t)=-\cos(2\pi ft)+0.5\sin(2\pi ft)$ 를 복소수 표현법과 polar coordinate representation으로 표기하시오.

정답: 복소수 표현방법으로 표기하자면 $V=-1-0.5j$ 이고, polar coordinate representation으로 표기하자면 $1.12\angle -153°$ 이다. 주의할 점은 $V=X+jY$ 는 $v(t)=X\cos(2\pi ft)-Y\sin(2\pi ft)$ 와 같다는 점이다.

3. phasor의 연산과 미분

phasor와 시간함수로 나타내는 회전운동의 몇 가지 연산을 비교해보도록 하자.

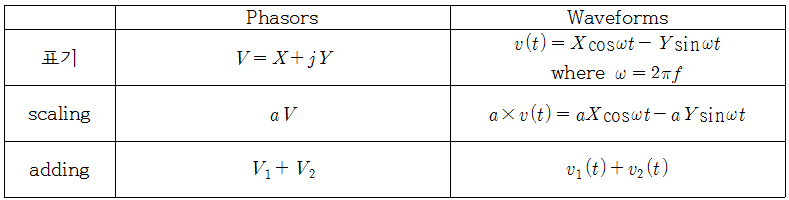
즉, 덧셈과 scaling은 phasor와 Waveform에서 같다. 곱셈과 나눗셈에 대해서도 생각해 볼 가치가 있지만, phasor를 이용한 신호 해석이 가장 의미가 있는 부분은 미적분이다.

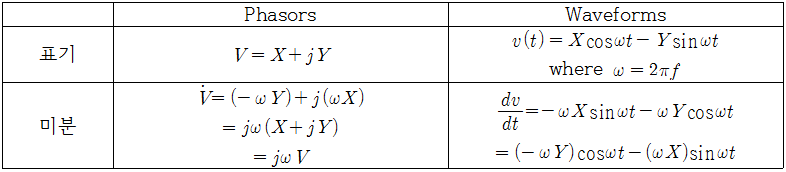
즉, phasor를 사용하게 되면 waveform을 미분해주는 것은 phasor에서는 단지 $j\omega$ 를 곱해주는 것만으로 가능하게 된다. 이것만으로도 미분방정식의 해석이 굉장히 쉬워진다.

다시 한번 강조하자면, $\frac{d}{dt}v(t)$ 와 $j2\pi f\times V$ 는 등가이다. 즉, 원래의 phasor 값에 $j2\pi f$ 를 곱해주기만 하면 미분을 대신 할 수 있다. 적분은 그 반대로 $j2\pi f$ 를 나눠주면 된다. 그렇다면 왜 $j$ 를 곱해주는 것이 미분과 등가가 될 수 있는 것일까?

다시 처음으로 돌아가면 모든 phasor는 sinusoidal wave의 다른 표현법이다. sine은 미분하면 cosine이 된다. 막대기로 생각하면 sine에서 cosine이 되는 것은 +90도 회전을 시켜주는 것과 같은 것이다.

또, cosine을 미분하면 -sine이 된다. 이것을 막대기로 생각하면 cosine에서 -sine이 되는 것은 +90도 회전을 시켜주는 것과 같은 것이다.

즉, sinusoidal wave는 미분했을 때 그 전체적 모양(sinusoidal)은 바뀌지 않고 막대기 회전의 시작 위치만 바뀐다. sinusoidal wave는 특이하게도 한번 미분해주면 위치가 바뀌는데 90도 회전을 하는 형태로 바뀐다. 허수란 무엇인가 편에서 보았겠지만 허수는 90도 회전을 의미하므로 미분과 회전은 sinusoidal wave에서 동등한 의미를 가지는 것이다. 따라서 sinusoidal wave를 복소수로 표현할 수 있게되면 $j2\pi f$ 를 곱해주는 것이 미분을 뜻할 수 있게 된다.

4. RLC 회로와 phasor

RLC 회로를 해석할 때, 캐패시터와 인덕터의 전압, 전류의 관계는 미분으로 표현된다고 배웠다. 캐패시터의 경우

\[i(t) = c {dv \over dt}\]

라는 공식을 통해 전압과 전류의 관계가 표현되는데, 이것을 phasor로 나타내게 되면

\[I = C \times j 2\pi f \times V\]

또는

\[V = I\times {1\over{j2\pi f C}}\]

가 된다. 옴의 법칙에서 $V=IR$이고, $L, C$의 저항값은 리액턴스라고 부르고 $X_L, X_C$ 라고 쓴다. 따라서 리액턴스 값은

\[X_C = {1\over {2\pi fC}}\]

이고³⁴⁵ 임피던스는

\[Z_C = {1\over {j2\pi fC}}\]

가 되는 것이다.

인덕터의 경우

\[v(t) = L {di \over dt}\]

라는 공식을 통해 전압과 전류의 관계가 표현된다. 이것을 phasor로 나타내면

\[V = L\times j 2\pi f \times I\]

로 표현할 수 있다.

따라서, 리액턴스는

\[X_L=2\pi fL\]

임피던스는

\[Z_L=j2\pi fL\]

로 표현할 수 있게 된다.