미분방정식을 보는 또 다른 관점

지금까지 미분방정식을 해석하는 여러가지 관점에 대해 알아보았다.

미분방정식을 이용한 현상 모델링편에서는 미분계수가 포함된 방정식을 미분방정식이라고 보았다.

또, 방향장과 오일러 방법 편에서는 좌표 $(x,y)$에 매핑된 기울기로 미분방정식을 기하학적으로 해석했으며,

자연상수 e와 제차 미분방정식 편에서는 미분방정식이란 연속성장의 관점에서 시시각각 변화율이 바뀌는 시스템의 관점에서 미분방정식을 해석하였다.

위의 세 가지 해석은 미분방정식을 수치적으로나 해석적(analytic)으로나 매우 유용한 관점이었으며, 1계 미분방정식 뿐만 아니라 그 이상의 degree의 미분방정식의 해 특성을 파악하는데에도 중요한 역할을 하는 주춧돌이었다.

---

지금부터는 미분방정식을 보는 또 다른 관점으로 바라보고자 한다. 여기서는 선형대수학에서 사용되던 벡터, 행렬의 개념을 함수에 도입할 것이다.

이제부터는 함수를 일종의 벡터로 취급할 수 있다는 것을 알 수 있게 되며, 선형대수학에서 행렬에 해당하는 연산이 ‘선형 연산자(linear operator)’라는 이름으로 개념이 확장된다.

또, 벡터들의 집합인 벡터 공간을 함수들의 집합인 함수 공간으로 개념을 확장시켜 사용할 것이다.

이런 논리가 아주 자세하게 학문으로 정립된 것이 ‘함수해석학’인데 이번 글에서는 기본적인 내용만 간단히 짚고 넘어가고자 한다.

Prerequisites

이번 포스팅을 이해하기 위해선 아래의 내용에 대해 자세히 알고 오시는 것을 추천드립니다. (사실상 선형대수학의 기초 전반은 모두 알아야 잘 이해할 수 있습니다.)

• 벡터의 기본 연산(상수배, 덧셈)
• 행렬 곱에 대한 또 다른 시각
• 행벡터의 의미와 벡터의 내적
• 행렬과 선형변환
• 4개 주요 부분 공간 간의 관계

functions as vectors

이전 포스팅 중 선형대수학의 기초 부분인 벡터의 기본 연산(상수배, 덧셈)에서는 세 가지 관점으로 벡터를 생각했다.

각각은 벡터란 화살표 같은 것, 숫자의 나열, 벡터 공간의 원소라는 정의였다.

그 중 벡터란 벡터 공간의 원소라는 정의가 가장 수학적인 정의라고 말한 바 있는데, 이 정의가 중요한 이유는 ‘이런 방식으로 벡터를 정의하는 것은 이러한 특성을 가진 것들은 모두 벡터로 취급해서 다룰 수 있다는 점을 강조한다’라고 언급했다.

다시 말해, 벡터의 특성을 가지는 개념을 발견한다면, 선형대수학에서 적용해볼 수 있었던 테크닉들과 개념들을 확장해 적용해볼 수 있게 되는 것이다.

조금 더 구체적으로 말하자면 어떤 수학적 object(가령, 벡터, 행렬, 함수, 등등…)가 벡터이기 위해선 다음의 두 가지 연산에 대해 닫혀있어야 한다.

• 벡터의 상수배
• 벡터의 합

너무 단순한가?

마치 쿠팡에서 로켓와우 멤버십 가입비 2900원만내면 쿠팡에서 제공하는 모든 로켓배송 서비스를 누릴 수 있는 것 처럼, 어떤 수학적 object가 위의 두 개의 법칙만 잘 만족하는 것이라고 확인된다면 ‘벡터’라는 멤버십을 받게 되는 것이다.

그리고 이에 따라 선형대수학에서 열심히 일궈놓은 개념들과 테크닉들을 적용받을 수 있게 된다.

그림 1. 쿠팡에서 로켓와우 멤버십에 가입해 누릴 수 있는 혜택들 (출처: 쿠팡)

엄밀한 증명은 아니지만 간단하게만 생각해봐도 함수는 벡터로 볼 수 있는 자격을 갖췄다.

아래는 함수의 상수배와 함수끼리의 합을 표현한 것이다.

\[(c\cdot f)(x) = c\cdot f(x) % 식 (1)\] \[(f+g)(x) = f(x)+g(x) % 식 (2)\]

다시 말해 어떤 함수 $f(x)$에 임의의 상수 $c$를 곱하더라도 여전히 $cf(x)$는 함수이고,

어떤 함수 $f(x)$와 $g(x)$를 더하더라도 $f(x)+g(x)$ 역시 함수다.

그림 2. 두 함수의 합
그림 출처: Function space, Wikipeda

이렇게 되면 벡터가 벡터 공간의 원소로 정의되었던 것 처럼, 함수도 벡터 공간의 원소로 정의될 수 있는 벡터가 되며, 이 때 함수가 포함되어 있는 벡터 공간을 “함수 공간(function space)”이라고 부른다.

---

우리는 벡터의 개념을 확장해서 함수 공간이라는 개념을 얻어낼 수 있음을 알게되었다.

이제 중요한 점은 어떻게 벡터에 적용되는 선형대수학의 개념들과 테크닉들을 함수에 적용할 것인가 라는 점이다.

개념의 확장이 있고 난 뒤에는 아무 의심없이 적용했던 모든 것들을 의심해봐야 한다.

이 개념이 어디서부터 나왔는지, 이 개념이 가졌던 근본적인 의미가 뭐였는지 생각해본 뒤에 비로소 확장된 버전의 테크닉들을 생각해낼 수 있기 때문이다.

여기서는 총 세 가지의 선형대수학의 개념에 대해 함수해석학에서 “확장된” 버전의 개념이 어떤 것인지 알아볼 것이다.

벡터 간의 내적 → 함수의 내적

첫 번째는 내적(inner product) 연산이다.

선형대수학에서 벡터의 내적은 다음과 같이 정의되었다.

임의의 아래와 같은 $n$차원 실수 벡터 $\vec{a}$와 $\vec{b}$에 대하여,

\[\vec{a} = \begin{bmatrix}a_1\\ a_2 \\ \vdots \\ a_n\end{bmatrix} % 식 (3)\] \[\vec{b} = \begin{bmatrix}b_1\\ b_2 \\ \vdots \\ b_n\end{bmatrix} % 식 (4)\] \[\text{dot}(\vec{a}, \vec{b})=a_1b_1 + a_2b_2 +\cdots + a_nb_n % 식 (5)\]

만약 $\vec{a}$와 $\vec{b}$가 복소 벡터였다고 하면 내적은 다음과 같이 정의된다.

\[\text{dot}(\vec{a}, \vec{b})=a_1^*b_1 + a_2^*b_2 +\cdots + a_n^*b_n % 식 (6)\]

여기서 $*$은 복소 켤레(complex conjugate) 연산이다.

왜 복소 벡터는 복소 켤레 연산이 들어가는지 생각해본다면 내적을 통해 복소 벡터에서 길이를 정의하기 위해서이다.

어떤 실수 벡터 $\vec{a}$의 크기(보통 L2-norm)는 다음과 같이 정의된다.

\[\text{norm}_2(\vec{a}) = \sqrt{a_1^2 + a_2^2 + \cdots + a_n^2} % 식 (7)\]

즉,

\[\text{norm}_2(\vec{a}) = \sqrt{\text{dot}(\vec{a}, \vec{a})}=\sqrt{a_1a_1+a_2a_2+\cdots+a_na_n} % 식 (8)\]

이 개념을 복소벡터에까지 확장시키면, 복소 벡터 $\vec{a}$에 대해서

\[\text{norm}_2(\vec{a})=\sqrt{a_1^2+a_2^2 + \cdots a_n^2}=\sqrt{a_1^*a_1+a_2^*a_2+\cdots +a_n^*a_n}=\sqrt{\text{dot}(\vec{a},\vec{a})} % 식 (9)\]

이어야 하므로 복소벡터의 내적연산은 식 (6)과 같이 정의되어야 하는 것이다.

이제 식 (6)의 방식을 확장해 함수의 내적을 정의해보도록 하자.

미분방정식을 다룰 때 사용되는 함수들은 실수 함수 범위에서 그치지않고 함수값이 복소수가 될 수 도 있기 때문에 다음과 같이 복소 벡터의 내적의 정의를 확장해 다음과 같이 정의한다.

실수 입력 복소수 출력을 갖는 구간 $(a, b)$에서 정의된 임의의 복소함수 $f$, $g$에 대해 두 함수의 inner product $\langle f, g\rangle$은

\[\langle f, g\rangle \equiv \int_a^bf^*(x)g(x) dx % 식 (10)\]

이다. 여기서 $f^*(x)$는 $f(x)$의 complex conjugate이다.

행렬과 벡터의 곱 → 연산자와 함수의 관계

행렬과 선형변환 편에서는 행렬은 벡터에 적용되는 일종의 함수라고 말한 바 있다.

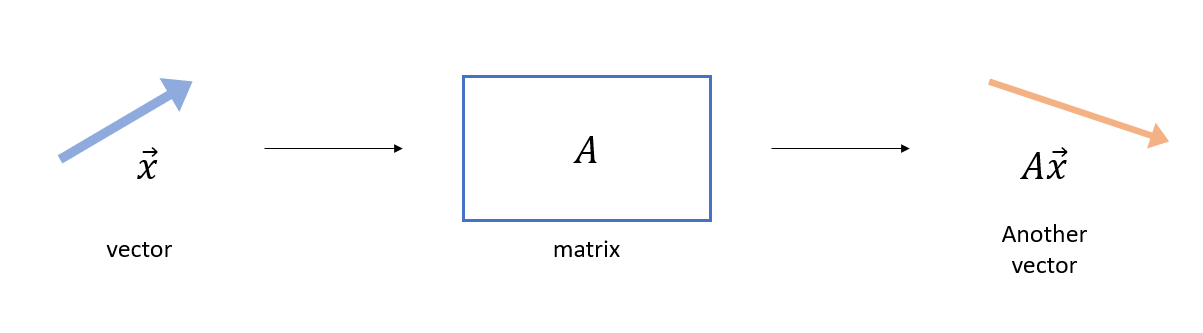
그림 3. 행렬은 벡터를 입력으로 받고 또 다른 벡터를 출력으로 내주는 일종의 함수 역할을 한다.

우리가 만약 일반적인 함수 $f(x)$, $g(x)$를 벡터로 생각할 수 있다면 선형대수학에서의 행렬의 개념을 확장시킨 함수를 입력으로 받고 다른 함수를 출력해주는 개념을 생각할 수 있다.

그러한 개념을 우리는 함수에 적용되는 ‘연산자(operator)’라고 부르자. 선형대수학의 행렬처럼 연산자는 함수를 입력받고 다른 함수를 출력해준다.

그리고, 특히 아래와 같은 특성을 만족하는 연산자라면 그 연산자는 ‘선형 연산자’라고 부른다. 어떤 연산자 $L$에 대해,

\[L(\alpha f + \beta g) = \alpha Lf + \beta Lg % 식 (11)\]

이며, $\alpha$와 $\beta$는 임의의 복소수이고, $f$와 $g$는 임의의 복소 함수이다.

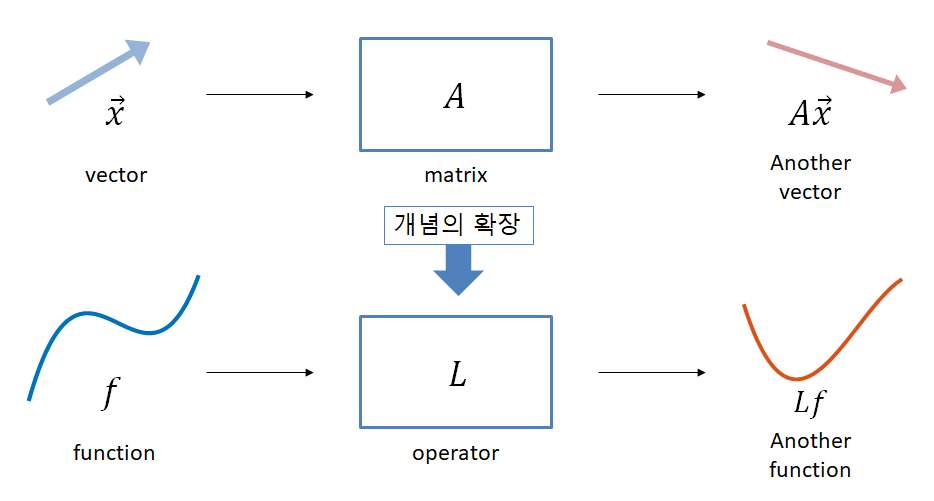
그림 4. 연산자(operator)란 함수를 입력으로 받고 또 다른 함수를 출력해주는 함수이다.

---

계속 추상적인 표현으로 ‘연산자’라고만 하면 이해하기 어렵기 때문에 아래와 같이 연산자의 쉬운 예시를 몇 가지 생각해보자.

연산자 $L$과 함수 $\phi(x)$에 대해,

(1) 스칼라배 연산

\[L\phi = \alpha \phi % 식 (12)\]

(2) 미분 연산자.

미분 차수는 몇 차(order)여도 상관없다.

\[L\phi = \frac{d^3}{dx^3}\phi \quad\text{ or }\quad L = \frac{d^3}{dx^3} % 식 (13)\]

또는 여러 개의 미분연산이 결합된 것도 하나의 연산자로 볼 수 있으며 다른 함수를 곱하고 미분을 취해주는 방식도 가능하다.

가령, 아래와 같은 연산자도 생각할 수 있으며 선형 연산자이다.

\[L\phi = \phi^{(n)}(x)+a_1(x)\phi^{(n-1)}(x)+\cdots+a_{n-1}(x)\phi'(x)+a_n(x)\phi(x) % 식 (14)\]

즉, 연산자는

\[L = \frac{d^n}{dx^n}+a_1(x)\frac{d^{n-1}}{dx^{n-1}}+\cdots+a_{n-1}\frac{d}{dx}+a_n(x) % 식 (15)\]

이다.

(3) 적분 연산자.

일반적인 적분 뿐만 아니라 다른 어떤 함수를 곱하고 적분을 취해주는 방식도 가능하다. 마찬가지로 선형연산자이다.

임의의 복소함수 $K(\cdot,\cdot)$에 대해,

\[L\phi = \int_{a}^{b}K(x, x')\phi(x')dx' % 식 (16)\]

가령 convolution 연산도 적분 연산자의 일종이다.

\[L\phi = \int_{-\infty}^{\infty}g(x-x')\phi(x')dx' % 식 (17)\]

또는 푸리에 변환도 적분 연산자의 일종이다.

\[L\phi = \int_{-\infty}^{\infty}e^{-2\pi i\xi x}\phi(\xi)d\xi % 식 (18)\]

전치 연산 → adjoint 연산

이번에는 전치 연산에 대해 생각해보자.

벡터의 전치 연산은 매우 간단하다. 아래와 같이 행과 열을 뒤집어 주면 된다.

\[\begin{bmatrix}1 & 2\end{bmatrix}^T = \begin{bmatrix}1\\2 \end{bmatrix} % 식 (19)\]

그럼 선형대수학에서 전치 연산의 역할은 무엇이었던가?

전치 연산은 열벡터를 행벡터로, 혹은 행벡터를 열벡터로 바꿔주는 역할을 해주었다.

행벡터의 의미와 벡터의 내적 편에서 보았던 것 처럼 행벡터는 열벡터에 적용되는 함수(functional)이다.

그리고 벡터의 전치 연산을 정의하고 행벡터를 열벡터에 작용하는 함수로 생각함으로써 두 벡터의 내적은 다음과 같이도 계산할 수 있게 되었다.

임의의 벡터 $\vec{a}$와 $\vec{b}$에 대해서,

\[\vec{a}\cdot\vec{b} = \vec{a}^T\vec{b} % 식 (20)\]

와 같이 쓸 수 있게 되는 것이다.

(이런 배경을 바탕으로 수학자들은 행벡터와 열벡터 간의 연산을 내적으로 정의하였다. 이 정의는 자연스레 행렬과 벡터의 곱의 정의로 확장되게 된다.)

즉, $\vec{a}$에 전치연산을 취해줌으로써 원래의 열벡터를 행벡터로 바꿔놓았고, 이를 통해 벡터의 기능을 연산자로 작동할 수 있게 해준 것이다.

여기서 말하고자 하는 핵심 포인트는 ‘전치 연산은 내적과 함께 생각해야 하는 것이며, 연산자에 작용시키기 위해 만든 연산’이라는 것이다.

---

한편, 임의의 두 벡터의 내적 연산을 생각해보는데 두 벡터 중 두 번째 벡터는 $A$라는 행렬을 통해 선형변환 된 결과로써의 벡터라고 생각해보자.

다시 말해, 임의의 두 벡터 $x$, $y$에 대해,

\[x\cdot Ay % 식 (21)\]

와 같은 내적연산을 생각해보자.

우리는 이 식을 통해 행렬 $A$의 전치 연산에 대해 생각해볼 것이다. 식 (20)에 따르면 식 (21)은 전치연산을 활용해 쓸 수 있다.

즉, 식 (21)은

\[x^TAy % 식 (22)\]

가 된다.

여기서 괄호를 조금 다르게 묶어서 생각해보면 식 (22)는 이렇게도 볼 수 있다.

\[(x^TA)y % 식 (23)\]

만약 이 식을 $x^TA$라는 벡터와 $y$라는 벡터의 내적으로 본다면, 식 (23)은 전치연산을 통해 다음과 같이 표현될 수도 있다.

\[(A^Tx)^Ty=(A^Tx)\cdot y % 식 (24)\]

여기까지 본 내용을 통해 벡터의 전치 연산을 함수 공간에 어떻게 확장시켰는지 알아보자¹.

두 함수 $\psi$와 $\phi$, 그리고 연산자 $L$에 대해 다음이 성립하게 하는 것을 연산자 $L$에 대한 adjoint 연산($^\dagger$, dagger라고 읽음)이다.

\[\langle \psi, L\phi \rangle = \langle L^\dagger \psi, \phi\rangle\]

여기서 $\langle \psi, \phi \rangle$은 $\psi$와 $\phi$ 간의 내적이다.

---

연산자를 설명할 때와 마찬가지로 추상적으로만 adjoint에 대해 설명하기 보단 몇 가지 예시를 들어서 확인해보도록 하자.

(1) 스칼라배 연산자의 adjoint

구간 $x\in [a, b]$에서 정의된 복소함수 $\phi$, $\psi$, $f$, $g$와 임의의 복소수 $\alpha$에 대해, 아래와 같은 연산자를 생각하자.

\[L\phi = \alpha \phi\]

그러면 $L^\dagger$는 다음을 만족해야 한다.

\[\langle f, Lg\rangle = \langle L^\dagger f, g\rangle\] \[\langle f, Lg \rangle = \int_{a}^{b}f^*(x)Lg(x)dx=\int_{a}^{b}f^*(x)\alpha g(x)dx\] \[=\int_{a}^{b}(\alpha^*)^*f^*(x)g(x)dx=\langle a^*f, g\rangle\]

이다. 따라서, $L^{\dagger}$는

\[L^{\dagger}\psi = \alpha^*\psi\]

와 같은 연산자이다. (여기서 $^*$는 complex conjugate)

(2) 미분 연산자의 adjoint

구간 $x\in [a, b]$에서 정의된 복소함수 $\phi$, $\psi$, $f$, $g$와 임의의 복소수 $\alpha$에 대해, 아래와 같은 연산자를 생각하자.

\[L\phi = \frac{d}{dx}\phi\]

그러면 $L^\dagger$는 다음을 만족해야 한다.

\[\langle f, Lg\rangle = \langle L^\dagger f, g\rangle\] \[\langle f, Lg \rangle = \int_{a}^{b}f^*(x)Lg(x)dx=\int_{a}^{b}f^*(x) \frac{dg}{dx}dx\]

부분적분을 이용하면 다음과 같이 계산된다.

\[\Rightarrow f^*(x)g(x)\big |_{a}^{b}-\int_{a}^{b}\frac{df^*}{dx}g(x)dx\] \[= f^*(x)g(x)\big |_{a}^{b}+\int_{a}^{b}\left(-\frac{df^*}{dx}\right)g(x)dx\] \[=f^*(b)g(b)-f^*(a)g(a) + \left\langle -\frac{d}{dx}f, g\right\rangle\]

따라서, $f^{\ast}(b)g(b) -f^{\ast}(a)g(a) = 0$이라는 조건 하에 다음과 같이 미분 연산자의 adjoint를 생각할 수 있다.

\[L^{\dagger}\psi=-\frac{d}{dx}\psi\]

---

또, 만약 아래와 같은 2차 미분이 포함된 연산자인 경우도 한번 생각해보자.

\[L\phi = p(x)\frac{d^2\phi}{dx^2}+q(x)\frac{d\phi}{dx}+r(x)\phi(x)\]

그러면 $L^\dagger$는 다음을 만족해야 한다.

\[\langle f, Lg\rangle = \langle L^\dagger f, g\rangle\]

여기서부터는 가독성을 위해 ‘$(x)$’라는 기호는 생략하여 수식을 조금 간략화하여 적도록 하자.

\[\langle f,Lg \rangle = \int_{a}^{b}f^*\left\lbrace p\frac{d^2g}{dx^2}+q\frac{dg}{dx}+rg\right\rbrace\] \[=\int_{a}^{b}f^* p \frac{d^2g}{dx^2}dx + \int_{a}^{b}f^* q \frac{dg}{dx}dx+\int_{a}^{b}f^* r gdx\]

여기서 $p(x)$, $q(x)$, $r(x)$의 위치를 이동시키면,

\[\Rightarrow \int_{a}^{b}pf^* \frac{d^2g}{dx^2}dx + \int_{a}^{b}qf^* \frac{dg}{dx}dx+\int_{a}^{b}rf^* gdx\]

와 같이 된다.

위 식에서 덧셈으로 합쳐진 세 개의 식 중 앞의 두 개의 식을 각각 따로 계산해보면 다음과 같이 계산된다.

i)

\[\int_{a}^{b} p f^* \frac{d^2g}{dx^2}dx=(pf^*)\frac{dg}{dx}\Big |_{a}^{b}-\int_{a}^{b}\frac{d}{dx}\left(pf^*\right)\frac{dg}{dx}dx\] \[=(pf^*)\frac{dg}{dx}\Big|_{a}^{b}-\left\lbrace\frac{d}{dx}\left(pf^*\right)g\Big |_{a}^{b}-\int_{a}^{b}\frac{d^2}{dx^2}\left(pf^*\right)g dx\right \rbrace\] \[=(pf^*)\frac{dg}{dx}\Big|_{a}^{b}-\frac{d}{dx}(pf^*)g\Big|_{a}^{b}+\int_{a}^{b}\frac{d^2}{dx^2}(pf^*)g dx\]

ii)

\[\int_{a}^{b}qf^*\frac{dg}{dx}dx=(qf^*)g\Big|_{a}^{b}-\int_{a}^{b}\frac{d}{dx}(qf^*)gdx\]

따라서, 원래의 식은 다음과 같이 묶어 쓸 수 있다.

\[\Rightarrow \left(pf^*\frac{dg}{dx}-\frac{d}{dx}(pf^*)g+(qf^*)g\right)\Big|_{a}^{b}+\int_{a}^{b}\frac{d^2}{dx^2}(pf^*)g-\frac{d}{dx}(qf^*)g+rf^*g dx\]

여기서 왼쪽의 식을 $J(f, g)$라 하면,

\[\Rightarrow J(f, g)+\left\langle \left(\frac{d^2}{dx^2}p^*(x)-\frac{d}{dx}q^*(x)+r^*(x)\right)f, g\right\rangle\]

따라서, $J(f, g)=0$ 이라는 조건 하에 다음과 같은 $L^{\dagger}$를 찾을 수 있다.

\[L^{\dagger}\psi=\frac{d^2}{dx^2}\Big(p^*(x)\psi(x)\Big)-\frac{d}{dx}\Big(q^*(x)\psi(x)\Big)+r^*(x)\psi(x)\]

$Ax=b$ in the world of functions

이번 포스팅에서 우리는 지금까지 함수를 일종의 벡터로 볼 수 있다는 사실을 통해 벡터로써의 함수와 그 함수에 가해질 수 있는 연산들의 특징을 살펴보았다.

그런데, 선형대수학이 행렬 $A$와 벡터 $x$, $b$에 대해 $Ax=b$를 놓고 해 $x$를 구하는 과정을 연구하는 과정에서 발전한 학문인 것과 같이,

우리는 연산자 $L$과 함수 $u$, $f$에 대해 $Lu=f$의 해 $u$를 구하는 과정을 잘 이해하는 것이 함수를 벡터처럼 다루고자 하는 궁극적인 목표라고 할 수 있다.

그러면 선형대수학에서 $Ax=b$의 해는 어떤 조건에서 존재했더라?

Existence of solution of $Ax =b$

바로 행렬 곱의 또 다른 시각편에서 보았던 것 처럼 $b$가 $A$의 열공간에 존재하고 있을 경우였다.

이것을 다른 시각에서 설명해보면 다음과 같이 설명할 수 있다. 우리는 주요 부분 공간(row space, column space, null space, left null space)의 관계를 이용해서 해의 존재 조건을 따져볼 것이다.

아래와 같은 조건을 만족하는 모종의 벡터 $y$를 생각해보자.

\[A^Ty=0\]

그러면 원래의 식 $Ax=b$에 대해 $y$와 내적을 취해보자.

\[Ax\cdot y = (Ax)^Ty = x^TA^Ty\]

위 식에서 괄호를 조금 다르게 쳐주면 다음과 같이 생각할 수도 있다.

\[\Rightarrow x^T(A^Ty)\]

여기서 $A^Ty=0$이라는 관계를 가진다고 하였으므로

\[x^T(0) = 0\]

이다.

그런데, $Ax=b$라는 관계에 의해 $(Ax)^Ty=b^Ty$ 이기도 하고, $(Ax)^Ty=0$이라는 사실을 확인했으므로 $b^Ty=b\cdot y = 0$이다. 따라서, $\vec{b}$와 $\vec{y}$는 서로 직교하는 벡터라는걸 알 수 있다.

그런데, 조금만 생각해보면 $y$는 left null space안에 있는 벡터라는 사실을 알 수 있다. left null space의 정의에 따라 그런 것이다.

그리고 4개 주요 부분 공간 간의 관계 편에서 배웠던 것 처럼 column space는 left null space와 항상 직교한다.

따라서 만약 $b$벡터가 $y$에 직교한다면 이 $b$벡터는 left null space와 직교하는 벡터 공간 안에 있는 것이므로 $b$는 column space안에 있는 벡터임을 알 수 있는 것이다.

그러므로, $Ax=b$의 해가 존재하는 조건은 $A^Ty=0$인 $y$에 대해 $b^Ty=0$인 것이다.

Solvability of $Lu = f$

우리는 함수 공간에서 연산자 $L$의 adjoint $L^\dagger$를 알아보았다.

위의 선형대수학에서의 논의를 함수 공간에 그대로 적용하면 $Lu=f$가 해를 가질 조건은 다음과 같다.

$L^\dagger v = 0$인 함수 $v$에 대하여 $Lu=f$에 $v$를 내적해보자.

그러면

\[\langle v, Lu\rangle = \langle v, f\rangle\]

이고, adjoint의 정의에 의해 위 식은 다음과 같다는 것을 알 수 있다.

\[\langle L^\dagger v, u\rangle = \langle v, f\rangle\]

여기서 $L^\dagger v=0$이므로 위 식의 좌변은 0이 된다. 따라서,

\[\langle v, f \rangle = 0\]

이라는 사실을 알 수 있다.

따라서, 위 선형대수학에서 $Ax=b$의 해의 존재조건과 유사하게 함수 공간에서 $Lu=f$의 해가 존재하기 위해서는 $f(x)$라는 함수가 adjoint 연산자의 영공간에 직교한다는 조건이 $Lu=f$가 해를 가지는 조건이다.

이 이론을 프레드홀름 정리 중 하나인 Fredholm alternative 라고 부르기도 한다.

참고 문헌

• function space, Wikipedia (https://en.wikipedia.org/wiki/Function_space)
• Applied Mathematical Methods in Theoretical Physics, 2nd ed., Wiley-VCH, Michio Masujima
• Advanced Differential Equations: Asymptotics & Perturbations, Arxiv, 2020, J Nathan Kutz