이번 포스트에서는 정규 분포(혹은 가우스 분포)의 공식을 유도해보고자 한다.

정규 분포의 공식은 꽤 복잡하기 때문에 아래의 그림과 같이 세 가지 파트로 나누어 유도해보도록 하자.

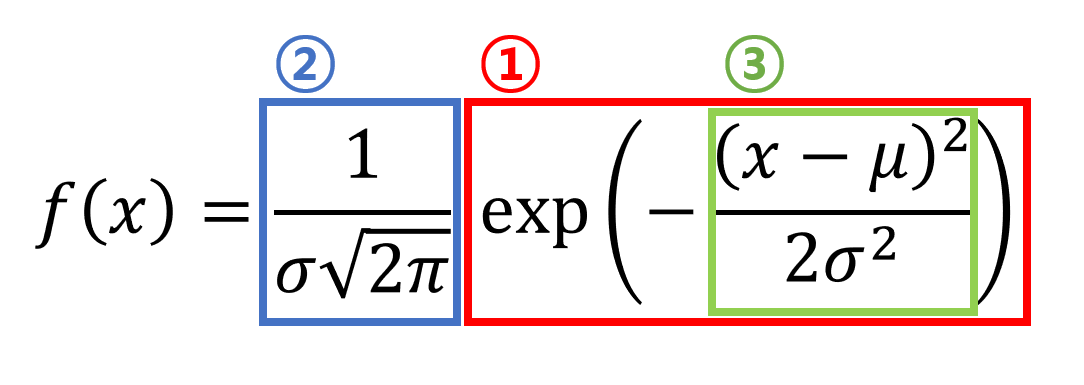
그림 1. 정규 분포의 공식과 포스팅에서의 유도 순서

prerequisites

이 포스팅에 대해 이해하시려면 아래의 내용에 대해 알고오시는 것이 좋습니다.

• 확률밀도함수의 개념과 특성
• 가우스 적분

$e^{-x^2}$의 꼴의 유도

우선은 $f(x)$가 $e^{-x^2}$의 꼴을 따른다는 것을 유도해보고자 한다.

필요 가정

이를 위해 아래와 같이 중심을 직교좌표계의 원점에 일치시킨 원형 다트 판에 다트 던지기를 하는 과정을 상상해보자.

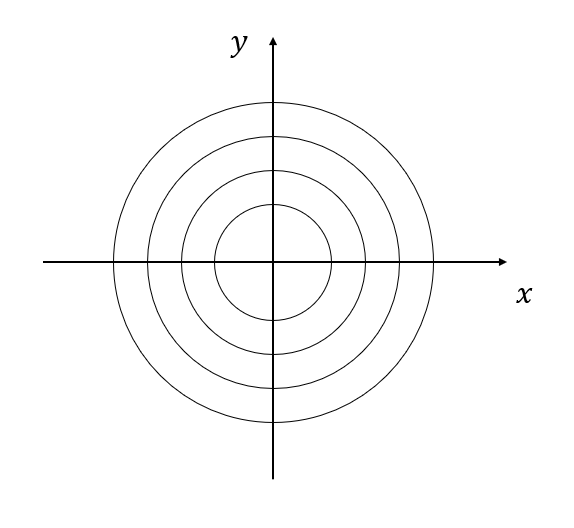
그림 2. 중심을 원점에 일치시킨 원형다트판

필요한 가정

1. 다트판 상에서 점수를 등고선으로 나타낸다고 했을 때, 동일한 점수의 등고선 상에 맞춘 다트는 모두 점수가 같다. 즉, 확률밀도 함수는 회전에 독립적이다.

2. 다트를 던져서 사각형 안에 맞추는 상황을 가정했을 때, 목표로 하는 사각형의 넓이가 같다면 원점으로부터 사각형까지의 거리가 가까울수록그 사각형에 맞을 확률이 높다.

3. 사각형까지의 거리가 같을 때 사각형의 넓이가 넓을 수록 맞을 확률이 높다.

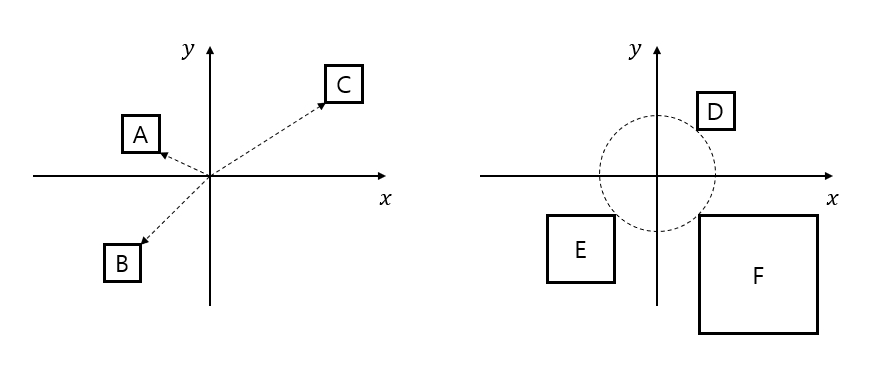
그림 3. (좌) 사각형의 크기가 같다면 거리가 가까울 수록 사각형에 맞을 확률이 높음. 즉, 사각형 A, B, C 순서로 다트가 맞을 확률이 높다. (우) 사각형까지의 거리가 같을 때 사각형의 넓이가 넓을 수록 맞을 확률이 높다. 즉, F, E, D 순서로 사각형에 맞을 확률이 높다.

유도 과정

앞서 언급한 세 가지의 가정을 생각하면서, 직교 좌표 상에 임의의 위치 $(x, y)$에서 너비가 $\Delta x$이고 높이가 $\Delta y$인 사각형 $A$에 다트가 맞을 기댓값을 생각해보자.

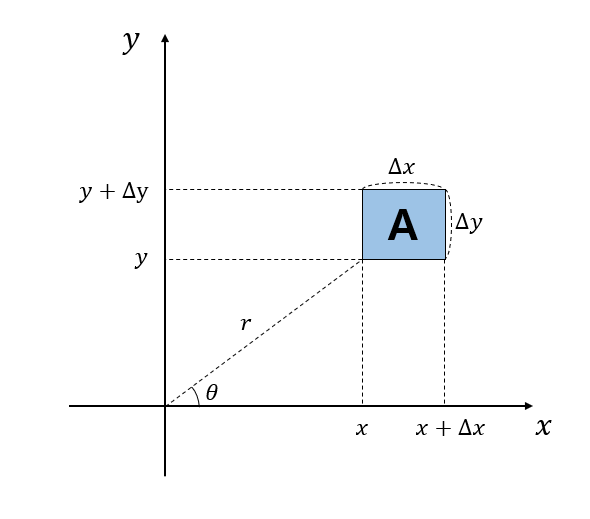
그림 4. 기댓값을 계산해볼 사각형 A

여기서 $x$축과 $y$축에서 다트가 안착할 확률에 대한 확률밀도 함수를 $f(x, y)$라고 하자.

이 때, $x$축과 $y$축에 다트가 안착할 확률은 서로 독립적이므로 $x$축과 $y$축에 대한 다트가 안착할 확률밀도함수는 각각 $f(x)$와 $f(y)$이다.

따라서, 사각형 $A$에 다트가 안착할 기댓값은 다음과 같다.

\[f(x)\Delta x f(y)\Delta y\]

한편, 위의 가정 중 회전에 관한 가정을 이용하기 위해 극좌표계를 이용해 같은 확률밀도를 서술해보자.

극좌표계에서 표현한 확률밀도함수를 $g(r,\theta)$라고 했을 때, 가정 1번에 따라 이 확률밀도함수는 회전에 독립적이므로 $g(r, \theta) = g(r)$이라고 써도 무관하다.

따라서, 사각형 A에 다트가 안착할 기댓값을 극좌표계를 이용해 서술하면 아래와 같다.

\[g(r)\Delta x\Delta y\]

이 때, 식 (1)과 식 (2)는 같은 값이므로,

\[f(x)\Delta x f(y) \Delta y = g(r) \Delta x \Delta y\]

이며, $\Delta x$와 $\Delta y$를 소거하면,

\[f(x)f(y) = g(r)\]

이다.

여기서 가정 1을 한번 더 이용해 식 (4)를 $\theta$에 대해 미분해주도록 하자.

그러면 확률밀도함수는 회전에 독립적이므로 회전에 대한 미분의 결과는 0이 되어야 한다.

\[\frac{df(x)}{d\theta}f(y) + f(x)\frac{df(y)}{d\theta}=\frac{g(r)}{d\theta} = 0\]

이 식은 아래와 같이 써주어도 무관하다.

\[\frac{df(x)}{dx}\frac{dx}{d\theta}f(y) + f(x)\frac{df(y)}{dy}\frac{dy}{d\theta}=\frac{g(r)}{d\theta} = 0\]

여기서 $x = r\cos(\theta)$, $y=r\sin(\theta)$이므로,

\[\frac{dx}{d\theta}=-r\sin(\theta)\] \[\frac{dy}{d\theta}=r\cos(\theta)\]

이다.

따라서, 식 (7)과 식 (8)을 식 (6)에 대입해주면,

\[식(6) \Rightarrow \frac{df}{dx}(-r\sin(\theta))f(y) + f(x)\frac{df}{dy}(r\cos(\theta))\]

여기서 $r\sin(\theta)=y$이고, $r\cos(\theta)=x$이므로,

\[\Rightarrow \frac{df}{dx}(-y)f(y) + f(x)\frac{df}{dy}x = 0\]

여기서 첫번째 항을 우변으로 넘겨 정리해주면 아래와 같다.

이 때 시각적인 편의를 위해, $df/dx = f’(x)$, $df/dy = f’(y)$로 적어주자.

\[\Rightarrow f(x)f'(y)x = f(y)f'(x)y\]

이제 이 식은 상미분방정식임이 확실히 보이는데, 변수분리법으로 풀어주기 위해 좌변과 우변을 $x$와 $y$에 대한 식으로만 나타내보자.

\[\Rightarrow \frac{xf(x)}{f'(x)}=\frac{yf(y)}{f'(y)}\]

식 (12)를 잘 보면 식 (12)가 의미하는 것은 양변에서 분자, 분모의 비율이 모두 일정하다는 것을 의미한다. 따라서 식 (12)의 양변의 값은 모두 어떤 상수 $C$와 같다고 할 수 있다.

\[식(12) \Rightarrow \frac{xf(x)}{f'(x)}=\frac{yf(y)}{f'(y)} = C\]

이제 식 (13)에서 미분 방정식을 풀어주도록 하자. $x$나 $y$나 같은 결과를 내기 때문에 $x$에 대해서만 풀어주자.

\[\frac{xf(x)}{f'(x)}=C\]

여기서 좌변에 $x$만 남기도록 식을 한번 정리해주자.

\[x = C\frac{f'(x)}{f(x)}\]

여기서 양변을 적분해주면,

\[\frac{1}{2}x^2=C \ln(f(x)) + C'\]

여기서 $C’$은 적분에 의해 생긴 또 다른 상수이다.

따라서 우리는 $f(x)$를 다음과 같이 쓸 수 있게 된다.

\[\therefore f(x) = A_0 \exp\left(\frac{1}{2}cx^2\right)\]

그런데, 가정 2번에 따르면 표적 중앙으로부터 거리가 가까울수록 맞을 확률이 높다고 하였기 때문에 식 (17)의 exponential term 내부의 값은 음수가 되어야 한다.

따라서, 식 (17)을 다음과 같이 서술하여 내부의 값이 음수임을 강조하도록 하자.

\[식(17) \Rightarrow f(x) = A_0 \exp\left(\frac{1}{2}(-kx^2)\right)\text{ where }k>0\]

$1/(\sigma\sqrt{2\pi})$의 유도

이번 꼭지에서는 앞서 유도한 식 (18)에서 $A_0$의 값이 $1/\sigma\sqrt{2\pi}$라는 것을 유도해보고자 한다.

확률밀도함수의 특성을 생각해보면 확률밀도함수의 전체면적은 1이 되어야 한다.

\[\int_{-\infty}^{\infty}f(x)dx = 1\]

따라서 다음 식이 만족되어야 한다.

\[\int_{-\infty}^{\infty}A_0 \exp\left(\frac{1}{2}-kx^2\right)dx = 1\]

여기서 $A_0$는 상수이므로,

\[\Rightarrow \int_{-\infty}^{\infty}\exp\left(\frac{1}{2}-kx^2\right)dx = \frac{1}{A_0}\]

식 (21)의 값을 $I$라고 하면,

\[\Rightarrow I^2 = \iint_{-\infty}^{\infty}\exp\left(-\frac{1}{2}k(x^2+y^2)\right)dxdy\]

인데, 중적분의 적분 domain을 직교좌표계에서 극좌표계로 바꿔써주면,

\[\Rightarrow I^2 = \int_{\theta = 0}^{\theta = 2\pi}\int_{r = 0}^{r=\infty}\exp\left(-\frac{1}{2}kr^2\right)rdrd\theta\]

이 된다¹.

여기서 다음과 같이 치환해주자.

\[-\frac{1}{2}kr^2 = u\]

그러면,

\[-krdr=du\]

이고,

\[rdr = -\frac{1}{k}du\]

이다.

따라서 식 (23)은 다음과 같이 쓸 수 있다.

\[식(23) \Rightarrow I^2 = \int_{\theta = 0}^{\theta = 2\pi}\int_{u = 0}^{u=-\infty}\exp\left(u\right)(-\frac{1}{k}du)d\theta\] \[= -\frac{1}{k}\int_{\theta = 0}^{\theta = 2\pi}\int_{u = 0}^{u=-\infty}\exp\left(u\right)(du)d\theta\] \[=-\frac{1}{k}\int_{\theta = 0}^{\theta = 2\pi}\left[e^u\right]_{0}^{-\infty}d\theta\]

여기서 $\exp(-\infty) = 0$이고 $\exp(0)=1$이므로,

\[\Rightarrow -\frac{1}{k}\int_{\theta = 0}^{\theta = 2\pi}(-1)d\theta\] \[=\frac{2\pi}{k}\]

따라서, 이 값은 원래의 $I^2$과 같으므로, $I$의 값은 아래와 같다.

\[I = \int_{-\infty}^{\infty}\exp\left(-\frac{1}{2}kx^2\right)dx=\sqrt{\frac{2\pi}{k}}\]

여기서 $I$의 값은 확률밀도함수의 넓이와 관련된 것이므로 항상 양수이기 때문에 $I$ 의 값은 양의 값만을 가지게 된다.

또, 식 (21)에서 $I$의 값은 $1/A_0$와도 같았으므로,

\[A_0 = \sqrt{\frac{k}{2\pi}}\]

이다.

따라서, 식 (18)을 다시 쓰면 다음과 같다.

\[식(18) = A_0 \exp\left(\frac{1}{2}(-kx^2)\right) = \sqrt{\frac{k}{2\pi}} \exp\left(\frac{1}{2}(-kx^2)\right)\text{ where }k>0\]

여기서 $k$에 대한 답을 얻어야 $A_0=1/(\sigma \sqrt{2\pi})$임을 알 수 있으므로 아래의 exponential 내부의 식 유도 부분에서 계속해서 식을 전개해보도록 하자.

exponential 내부의 식 유도

그림 1에 있는 정규 분포의 공식에서 exponential term 안에 있는 내부의 식을 유도하기 위해선 확률밀도함수의 moment 개념을 이용해야 한다.

어려운 것은 아니고 다음과 같이 확률밀도 함수 $f(x)$가 주어져있을 때 평균과 분산은 다음과 같이 계산할 수 있다는 것이다.

\[\mu=\int_{-\infty}^{\infty}xf(x)dx\] \[\sigma^2 = \int_{-\infty}^{\infty}x^2f(x)dx\]

우리는 식 (34)까지 구했던 $f(x)$의 식을 이용해서 평균과 분산 값을 적어보도록 하자.

\[\mu = \int_{-\infty}^{\infty}x\sqrt{\frac{k}{2\pi}}\exp\left(-\frac{1}{2}kx^2\right)dx\]

식 (37)에서 $x$ term은 기함수이고 $\exp\left(-\frac{1}{2}kx^2\right)$ term은 우함수이다. 따라서, 기함수 곱하기 우함수는 기함수이므로, 위의 식 (37)의 결과값은 0이 된다.

또, 분산 값을 적어보면,

\[\sigma^2 = \int_{-\infty}^{\infty}x^2\sqrt{\frac{k}{2\pi}}\exp\left(-\frac{1}{2}kx^2\right)dx\] \[=\sqrt{\frac{k}{2\pi}}\int_{-\infty}^{\infty}x^2\exp\left(-\frac{1}{2}kx^2\right)dx\]

여기서 식 (39)를 다음과 같이 생각해보자.

\[\Rightarrow \sqrt{\frac{k}{2\pi}}\int_{-\infty}^{\infty}x\cdot x\exp\left(-\frac{1}{2}kx^2\right)dx\]

여기서 부분적분을 이용해 식 (40)을 적분해보자.

$x$를 $u$ 라고 하고 $x\exp\left(-\frac{1}{2}kx^2\right)$을 $dv$라고 하면,

\[\begin{cases}u = x \\ du = 1\end{cases}\] \[\begin{cases} dv = x\exp\left(-\frac{1}{2}kx^2\right) \\ v = -\frac{1}{k}\exp\left(-\frac{1}{2}kx^2\right) \end{cases}\]

임을 알 수 있다.

따라서, 식 (40)의 적분 값은 다음과 같다.

\[식(40)\Rightarrow \sqrt{\frac{k}{2\pi}}\left\lbrace\left[x\cdot\left(-\frac{1}{k}\right)\exp\left(-\frac{1}{2}kx^2\right)\right]_{-\infty}^{\infty}+\frac{1}{k}\int_{-\infty}^{\infty}\exp\left(-\frac{1}{2}kx^2\right)dx\right\rbrace\]

식 (43)에서 대괄호([])안에 있는 term에 대해 먼저 생각해보면 무한대 값에 대해서는 $x$는 무한대로 발산하고 exponential term은 0으로 수렴하게 되는데, 수렴 속도는 exponential이 0으로 수렴하는 속도가 더 빠르다. 이는 음의 무한대 값에 대해서도 마찬가지로 exponential term이 0으로 수렴하는 속도가 더 빠르다. 따라서 대괄호 안에 있는 term은 결국 0이 되게 된다.

따라서 식 (43)은

\[식(43) \Rightarrow \sqrt{\frac{k}{2\pi}}\left\lbrace\frac{1}{k}\int_{-\infty}^{\infty}\exp\left(-\frac{1}{2}kx^2\right)dx\right\rbrace\]

여기서 식 (44) 중괄호($\lbrace\rbrace$)안에 있는 값은 식 (32)로부터 알 수 있는 값이다.

\[\Rightarrow \sqrt{\frac{k}{2\pi}}\left(\frac{1}{k}\right)\sqrt{\frac{2\pi}{k}} = \frac{1}{k}\]

그리고 이 값은 원래 $\sigma^2$ 였으므로,

\[\therefore k = \frac{1}{\sigma^2}\]

이다.

다시 식 (34)에 $k$값을 대입해주면,

\[식(34) \Rightarrow f(x) = \sqrt{\frac{k}{2\pi}}\exp\left(-\frac{1}{2}kx^2\right) = \frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{x^2}{2\sigma^2}\right)\]

이 되며, 이 수식은 정규 분포의 수식에서 평균값이 $0$인 경우를 의미하며 평균값이 $\mu$인 경우에는 $x$를 $x-\mu$로 평행 이동 시켜주면 되기 때문에 최종적인 정규 분포의 공식은 다음과 같다.

\[\Rightarrow \frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]

reference

• The Normal Distribution: A derivation from basic principles, Dan Teague, The North Carolina School of Science and Mathematics (https://www.alternatievewiskunde.nl/QED/normal.pdf)