DTFS의 유도 과정은 CTFS의 유도 과정과 거의 흡사하다고 할 수 있다. 삼각함수의 orthogonality를 이용해서 주기 함수를 decompose한다는 개념이 동일하게 이용된다.
Prerequisites
이 포스팅을 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
이산 정현파 신호의 주파수 특성
이산 신호는 연속 신호를 시간 샘플링해 얻은 것이다. 얼핏 생각하면 샘플링 주기를 매우 짧게 만들어주면 연속신호처럼 보이기 때문에 연속신호와 별다른 차이없이 분석을 수행할 수 있을 것이라고 생각할 수 있다.
그러나, 샘플링을 통해 얻게되는 부수적인 효과로 이산 정현파만의 특이한 주파수 특성을 보이게 된다.
이산시간 푸리에 급수에서도 연속 시간 푸리에 급수에서와 마찬가지로 복소 정현파를 이용해 주기 신호를 분석한다.
따라서, 우리는 샘플링된 복소 정현파에 대해 생각해보자.
가령 주기가 6인 복소 정현파는 다음과 같이 표현할 수 있다.
\[\exp\left(j\frac{2\pi n}{6}\right)\text{ where } n\in \mathbb{N}\]여기서 $n$이 0일 때부터 값을 넣어가며 복소 평면에 좌표를 찍어보면 다음과 같은 결과를 확인할 수 있다.
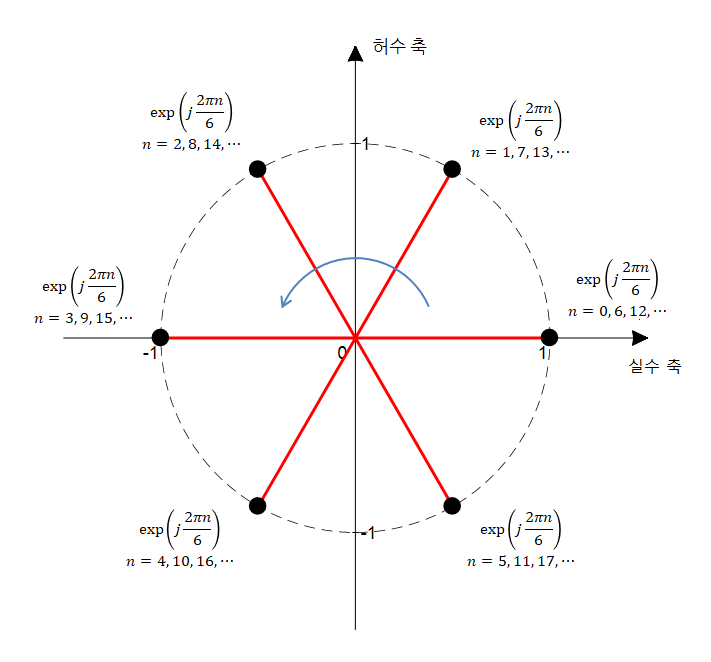
그림 1. 주기가 6인 복소 정현파
즉 주기가 6인 복소 정현파의 값은 복소 평면 위의 단위원을 6등분한 호 위의 점들 6개의 값과 대응된다.
그리고 단위원 위의 6개 점들은 원의 특성상 $2\pi$의 주기성을 띈다. 쉽게 말해서 복소 평면 상의 (1,0) 점이라도 한 바퀴를 돌아서 온 점인지 두 바퀴를 돌아서 온 점인지 알 수가 없다는 의미이다.
그러므로, 이산 신호에서는 각주파수가 $2\pi$의 정수배만큼 혹은 주파수가 1의 정수배만큼 차이나는 이산 정현파들은 동일한 신호라는 것을 알 수 있다. 또 다른 관점에서 보면 이산 신호의 주파수 스펙트럼은 각주파수 $2\pi$ 혹은 디지털 주파수 $1$을 주기로 하는 주기함수이다.
아래 그림은 주기 신호의 스펙트럼과 그것을 시간 샘플링하여 이산화 했을 때의 결과물을 비교한 것이다.
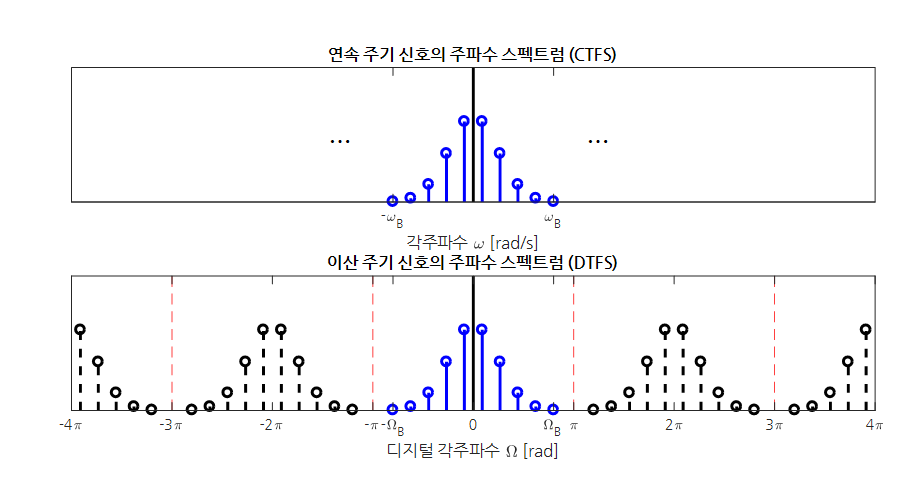
그림 2. 이산 주기 신호의 주파수 스펙트럼은 원래 연속 주기 신호의 복사물이 $2\pi$ 간격으로 표시되게 된다.
또, 아래 그림은 비주기 신호의 스펙트럼과 그것을 시간 샘플링하여 이산화 했을 때의 결과물을 비교한 것이다.
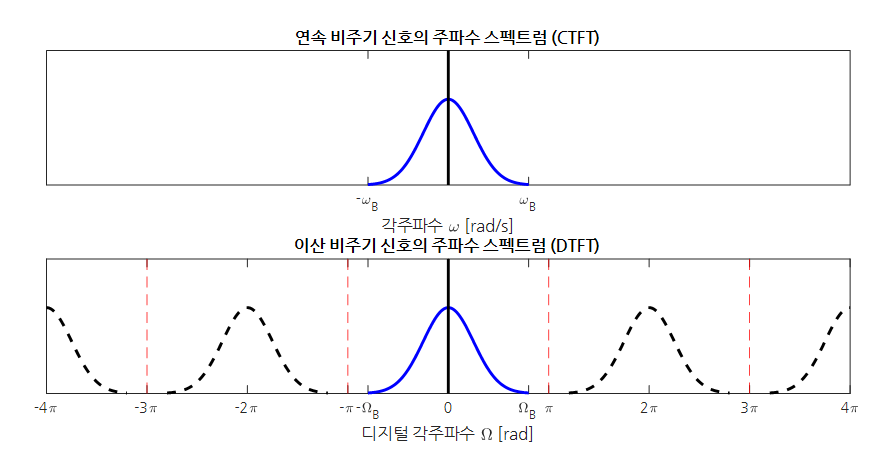
그림 3. 이산 비주기 신호의 주파수 스펙트럼은 원래 연속 신호의 복사물이 $2\pi$ 간격으로 표시되게 된다.
이산 시간 푸리에 급수
이산 시간 푸리에 급수(Discrete Time Fourier Series, DTFS)는 주기 이산신호에 대해 적용할 수 있는 푸리에 해석 방법이다.
주기 이산신호란 정수인 주기 $N$에 대해 $x[n+N] = x[n]$을 만족하는 이산신호를 말한다.
가령, 아래의 신호는 주기가 6인 이산신호라고 할 수 있다.
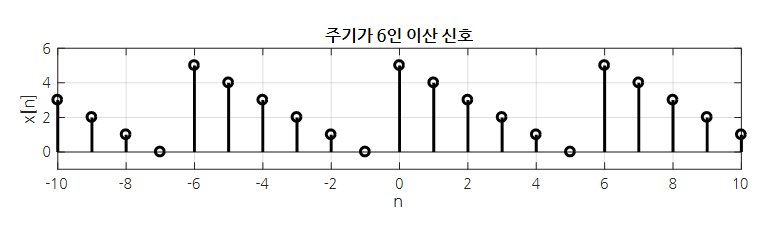
그림 4. 주기가 6인 이산 신호
DTFS는 푸리에 급수와 기본적인 개념이 크게 다르지 않아 정현파를 선형결합하여 원래 신호를 표현하며, 복소 정현파를 사용하는 것이 일반적이다.
(복소 정현파를 이용하는 이유에 대해서는 신호 공간(signal space)편의 고유함수 파트를 참고)
우리가 분석하고자 하는 이산 신호의 주기가 $N$이라면 이 신호의 기본 주파수는 $1/N$이며, $k$배의 고조파 주파수는 $k/N$임을 쉽게 알 수 있는데, 앞서 언급한 “$2\pi$ 주기성”에 의해 k 고조파와 $k+N$, $k+2N$, $\cdots$ 고조파는 서로 구별할 수 없다는 것을 알 수 있다. 다시 말해,
\[\exp\left(j\frac{2\pi}{N}(k+mN)n\right)=\exp\left(j\frac{2\pi}{N}kn\right)\exp\left(j2\pi m n\right)=\exp\left(j\frac{2\pi}{N}kn\right)\]이다.
그러므로 이산 주기 신호에 대해서는 서로 다른 주파수 성분이 $N$개를 넘을 수 없다.
그러므로 원래의 주기 신호 $x[n]$은 총 $N$ 개의 이산 복소 정현파의 선형 결합으로 표현할 수 있다.
\[x[n]=\sum_{k=0}^{N-1}a_k\exp\left(j\frac{2\pi k}{N}n\right)\]이산 복소 정현파의 직교성
푸리에 급수에서 확인했던 것 처럼 서로 다른 주파수 복소 정현파는 서로 직교한다.
주기 N에 대하여 두 이산 신호 $\phi_k[n]$ 와 $\phi_p [n]$ 는 다음이 성립할 때 직교한다고 할 수 있다.
\[\sum_{n=0}^{N-1}{\phi_k[n]\phi^*_p[n] =0 \text{ when } k\neq p }\]여기서 $\phi^*_p[n]$ 에서 ‘*’ 는 켤레복소수 연산이다.
우리는 이제 아래와 같은 집합 내의 이산 복소 정현파의 직교성에 대해 알아보도록 하자.
\[\left\{ \phi_k[n] | \phi_k[n] = \exp\left(j \frac{2\pi k}{N}n\right)\text{ where } k = 0, 1,2,\cdots, N-1 \right\}\]이산 시간 영역에서의 직교성의 정의에 의하여
\[\sum_{n=0}^{N-1}{\phi_k[n]\phi^*_p[n]}\] \[=\sum_{n=0}^{N-1} \exp\left(j \frac{2\pi k}{N}n\right)\exp\left(-j \frac{2\pi p}{N}n\right)\] \[=\sum_{n=0}^{N-1} \exp\left(j \frac{2\pi (k-p)}{N}n\right)\] \[=\sum_{n=0}^{N-1} \left\lbrace \exp\left(j\frac{2\pi(k-p)}{N}\right)^n\right\rbrace\]이제 정수 $k$, $p$ 에 대하여 두 가지 경우가 있을 수 있다.
1) $k=p$ 인 경우
\[\Rightarrow\sum_{n=0}^{N-1}{\exp\left(j\frac{2\pi n}{N}(0)\right)} = N\]1) $k\neq p$ 인 경우
식 (9)를 자세히 보면 초항이 1이고 공비가
\[\exp\left(j \frac{2\pi (k-p)}{N}\right)\]인 등비급수의 합을 나타내는 것으로 볼 수 있다.
일반적으로 초항이 $a$ 이고 공비가 $r$ 인 등비급수의 합은 다음과 같다.
\[S_n = a\left(\frac{1-r^n}{1-r}\right)\]따라서, 등비급수 합의 공식을 이용하여 식 (9)는 다음과 같이 바꿔 쓸 수 있다.
\[\Rightarrow \frac {1-\exp\left(j \frac{2\pi(k-p)}{N}\right)^N} {1-\exp\left(j \frac{2\pi(k-p)}{N}\right)}\]분자에 대해 지수법칙을 이용하면,
\[=\frac {1-\exp\left(j2\pi(k-p)\right)} {1-\exp\left(j\frac{2\pi(k-p)}{N}\right)} = 0\]위 식에서 정수 $n$에 대하여, $\exp(j2\pi n) = 1$ 이므로 위 식의 값은 0이다.
따라서, 서로 다른 주파수 복소 정현파는 서로 직교한다.
이산 푸리에 급수 공식 유도
DTFS의 공식은 이산 복소 정현파의 직교성(orthogonality) 성질을 이용하여 얻을 수 있다.
주기가 $N$ 인 이산신호 $x[n]$ 에 대하여,
\[x[n] = x[n+N]\] \[x[n] = \sum_{k=0}^{N-1}{a_k \space \exp\left(j \frac{2\pi k}{N}n\right)}\]where
\[a_k =\frac{1}{N}\sum_{n=0}^{N-1}x[n] \exp\left(-j \frac{2\pi k}{N}n\right) \text{ for }k= 0, 1, \cdots, N-1\]여기서 DTFS에서의 상수항인 $a_k$의 유도과정은 다음과 같다.
이산 시간 도메인에서의 직교성의 성질을 이용하기 위해 $x[n]$ 에 $\phi^*_r[n]$ 을 곱하여 summation을 취해보자.
\[\sum_{n=0}^{N-1}x[n]\phi^*_r[n]\]DTFS의 정의에 의해 $x[n]$을 치환하면,
\[=\sum_{n=0}^{N-1} \left(\sum_{k=0}^{N-1}{a_k \space \exp\left(j \frac{2\pi k}{N}n\right)}\right) \phi^*_r[n]\]여기서 $\exp\left(j \frac{2\pi k}{N}n\right)$ 을 $\phi_k[n]$ 으로 대체해 생각하면 아래와 같이 바꿔 쓸 수 있다.
\[=\sum_{n=0}^{N-1} \left(\sum_{k=0}^{N-1}{a_k \space \phi_k[n]}\right) \phi^*_r[n]\]여기서 summation의 위치를 서로 바꾼 뒤 $a_k$를 가장 안쪽의 summation 왼쪽으로 옮기면 아래와 같이 바꿔 쓸 수 있다.
\[= \sum_{k=0}^{N-1}a_k\sum_{n=0}^{N-1}\phi_k[n]\phi^*_r[n]\] \[=\sum_{k=0}^{N-1}a_kN\delta[k-r]\] \[= N a_r\]따라서, DTFS의 계수는 다음과 같다.
\[a_k =\frac{1}{N}\sum_{n=0}^{N-1}x[n] \exp\left(-j \frac{2\pi k}{N}n\right) \text{ for } k = 0, 1, \cdots, N-1\]참고 문헌
- 디지털 신호 처리, 이철희, 한빛아카데미