Prerequisites

본 포스팅을 더 잘 이해하기 위해서는 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 표본과 표준 오차의 의미
• 표본 분산은 n 대신 n-1로 나눈다
• p-value의 의미
• 신뢰 구간의 의미

추정량과 표준 오차

추정량의 의미

잭나이프와 부트스트랩 방법을 이해하기 위해선 추정량(estimator)이라는 것이 무엇인지에 대해 이해하는 것이 필수적이다.

추정량이란 표본들을 이용해 계산하는 함수라고 할 수 있다.

(도대체 어떤 놈이 번역했는지, 번역이 ‘량’으로 되어서 어떤 quantity를 의미하는 것만 같다. 이것 또한 잘못된 번역이 아닌가 싶다. 추정방법, 추정자 내지는 추정함수라고 번역하는 것이 더 옳아 보인다.)

가령 평균을 구하는 함수, 분산을 구하는 함수는 모두 추정량이다.

평균값은 다음과 같이 계산된다. $n$개의 샘플 $x_1, x_2, \cdots, x_n$에 대해,

\[m(X)=\frac{1}{n}\sum_{i=1}^{n}x_i\]

와 같다. $m(\cdot)$은 일종의 함수로써 $x_1, x_2, \cdots, x_n$을 입력으로 받아 정해진 계산을 수행한다.

이와 같은 맥락에서 임의의 추정량(estimator)을 정의할 수 있다.

내가 임의로 정한 추정량을 $\phi_n$이라고 해보자. 어차피 함수를 정의하는 것과 같은 맥락이기 때문에 어렵지 않게 아무거나 하나 정의해보자.

\[\phi_n(X)=\frac{3}{2}\sum_{i=1}^{n}\log(x_i)\]

또, 추정량은 출력값이 꼭 하나일 필요는 없다. 출력값이 두 개인 추정량도 존재한다. 이런 경우를 interval estimator라고 하고 신뢰구간 추정량이 대표적이다.

표준 오차의 의미

한편, 표본과 표준 오차의 의미 편에서는 평균값의 표준 오차에 대해 생각해보았다.

평균이라는 것은 여기서 표본 평균을 말하는데, 우리가 다루는 거의 대부분의 데이터들은 모집단에서 추출한 표본이다.

그리고 이용하는 추정량 또한 표본에 대해 적용하게 되는 것들이다.

다시 한번 표본의 표준 오차에 대해 생각하는 이유를 생각해보면, 표본이란 모집단에서 일부 추출한 subset이기 때문이다.

다시, 조금 더 쉽게 예를 들어 아래와 같이 150명의 금성에 사는 외계인의 키를 조사한 분포를 생각해본다고 하자.

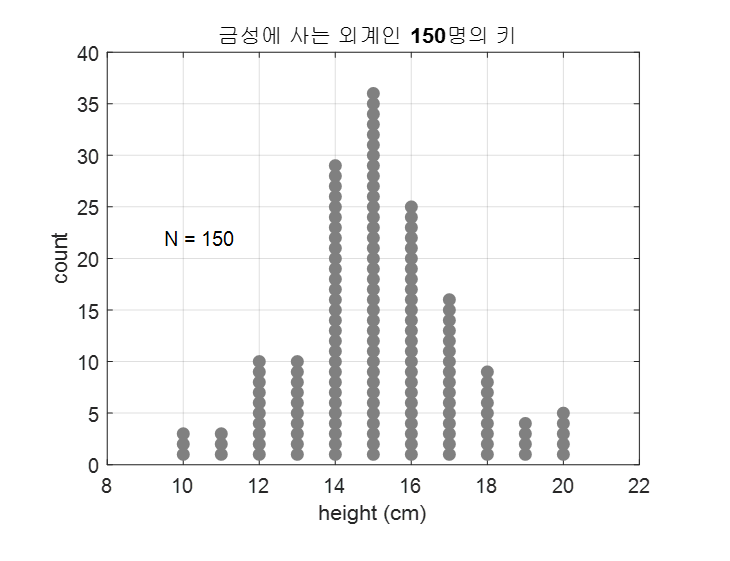
그림 1. 상상속의 모집단인 금성 외계인 150명의 키 분포

여기서 임의로 6명의 금성 외계인을 뽑는다고 하면, 그 때 마다 표본의 분포는 달라질 것이고, 추정값(가령 평균, 표준편차)도 달라질 것이다.

아래의 그림 2에서는 표본 추출을 세 번 수행해 본 것이다.

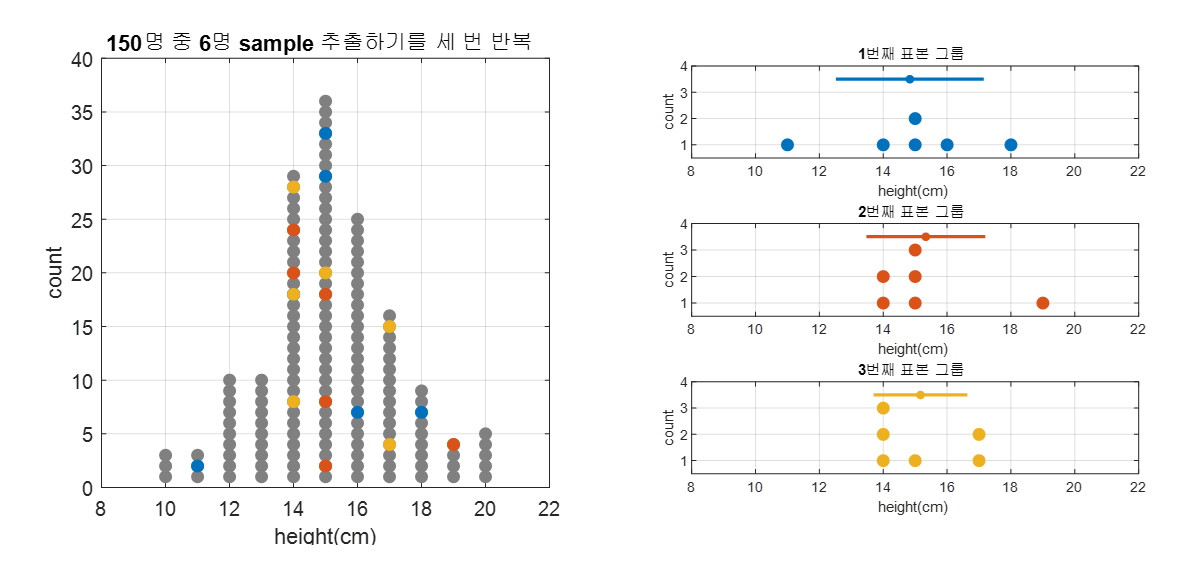
그림 2. 세 번 표본을 추출해보고 그 때 마다 얻게되는 표본 분포를 그린 것

우리가 궁금한 것은 임의의 추정량 $\phi_n$에 대해 추정량의 오차(즉, 추정값의 표준 편차)가 어떻게 계산 되는지에 관한 것이다.

다시 말해 $std(\phi_n)$이 어떻게 계산 되는지가 바로 이 추정량의 표준오차이다.

표본 평균의 표준 오차는 계산 방법이 이론적으로 잘 정립되어 있다.

그런데, 이론적으로 잘 확인되어 있지 않은 추정량이라도 표준 오차를 계산해줄 수 있는 신박한 방법이 없을까?

잭나이프 방법과 부트스트랩 방법은 이렇듯 추정량의 표준 오차를 계산해주는 방법이다.

이 때, 두 방법 모두 비모수적인 접근으로 추정량의 표준 오차를 계산해주며, resampling 방법에 기반한 방법이라는 점 또한 동일하기 때문에 한꺼번에 놓고 두 방법을 이해해보도록 하자.

잭나이프(jackknife) 방법

잭나이프 방법의 유래

잭나이프 방법은 Quenoulle와 Tukey에 의해 1949-1956년에 걸쳐 개발된 테크닉이라고 할 수 있다.

잭나이프 방법이 ‘잭나이프’라는 이름을 갖게 된 것은 실제 잭나이프의 생김새처럼 데이터를 다루기 때문이다.

그림 3. 잭나이프의 생김새는 이런 형태다.

잭나이프 방법은 큰 분류로는 resampling에 기인한 방법인데, 잭나이프 방법은 주어진 데이터에서 하나 씩 빼가면서 새로운 데이터셋을 구성한다.

예를 들어 (a,b,c,d)라는 데이터셋이 주어져있다고 하면 잭나이프 방법으로는

(b,c,d), (a,c,d), (a,b,d), (a, b, c)

의 네 가지 새로운 데이터셋을 얻게 되는 것이다.

잭나이프에서 칼이 하나 하나씩 빠져나와 사용되는 것과 같은 모습을 띈다.

데이터를 하나 하나 빼보면서 새로운 데이터 셋을 얻는 이유는 이미 갖고 있는 데이터들을 이용해서 resampling을 함으로써 추정량의 오차 범위를 추정해볼 수 있기 때문이다.

다시 말하자면, 잭나이프 방법에서는 어떤 estimator의 출력 범위를 파악해보기 위해 부품을 하나 하나씩 빼보면서 작동하는 일을 한다¹.

그리고 이를 통해 기기의 전체적인 오차 범주를 파악해 볼 수 있게 되는 것이다.

잭나이프 방법의 사용법

그렇다면 잭나이프 방법의 구체적인 사용방법은 어떻게 될까?

우선 용어를 살짝 정의하자.

임의의 추정량(estimator) $\phi$에 대하여 $\phi_n(X)=\phi_n(X_1, \cdots, X_n)$은 표본 $X=\lbrace X_1, X_2, \cdots, X_n \rbrace$에 대해 정의되는 추정값이다.

여기서 subscript $n$은 $n$개의 표본에 대해 추정하는 것임을 강조하는 의미로 쓴 것이다.

그리고 $n$개의 표본 $X$에서 $i$번째 표본을 제외한 집합을 $X_{[i]}$와 같이 쓰도록 하자.

이제, 잭나이프 방법을 적용할 estimator $\phi$에 대해 다음과 같은 값을 생각해보자.

\[ps_i(X)=n\phi_n(X)-(n-1)\phi_{n-1}(X_{[i]})\]

위 값의 $ps$는 pseudo-value의 앞 두 글자만을 따온 것인데, pseudo-value의 의미는 모든 데이터를 다 이용해서 얻은 추정값에서 $i$번째 데이터만 제외해서 얻은 추정값을 빼준 것이다.

다시 말하면 pseudo-value는 전체 데이터를 모두 이용해 얻은 추정값에서 $i$ 번째 데이터가 미치는 영향력이 얼마 만큼인지를 보여주는 값이라고 할 수 있다.

그러면 $ps_i(X)$의 평균값은

\[ps(X)=\frac{1}{n}\sum_{i=1}^{n}ps_i(X)\]

이고 분산은

\[V_{ps}(X)=\frac{1}{n-1}\sum_{i=1}^{n}(ps_i(X)-ps(X))^2\]

이라는 것을 알 수 있는데, $ps_i(X)$를 독립적인 표본(샘플)들로 본다고 하면 표본평균 $ps(X)$의 95% 신뢰구간은 표본평균 $\pm$ 1.96SEM이라는 관계에서[^2]

\[\left(ps(X)-1.96\sqrt{\frac{1}{n}V_{ps}(X)}, ps(X)+1.96\sqrt{\frac{1}{n}V_{ps}(X)}\right)\]

와 같이 계산할 수 있으며 아래와 같이 z-value를 정의하면 p-value도 정할 수 있게 된다. 여기서 귀무가설은 $H_0: \theta =\theta_0$이라고 하자. 그러면,

\[Z=\frac{\sqrt{n}(ps(X)-\theta_0)}{\sqrt{V_{ps}(X)}}=\frac{ps(X)-\theta_0}{\sqrt{(1/n)V_{ps}(X)}}\]

잭나이프 사용 예시

아래와 같이 16개의 데이터가 주어졌다고 생각해보자.

\[17.23,\ 13.93,\ 15.78,\ 14.91,\ 18.21,\ 14.28,\ 18.83,\ 13.45 \\ 18.71,\ 18.81,\ 11.29,\ 13.39,\ 11.57,\ 10.94,\ 15.52,\ 15.25\]

여기서 우리는 아래와 같은 estimator를 상정해보자.

\[\phi_n(X_1, \cdots,X_n)=\log(s^2)=\log\left(\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2\right)\]

일단 모든 16개의 데이터를 이용해 $\phi_n(X)$를 먼저 계산해보면

\[\phi_n(X)= 1.9701\]

이라는 것을 알 수 있다 (여기서 log는 자연로그이다).

여기서 각 데이터에 대해 각 데이터를 제외하고 계산한 $\phi_{n-1}(X_{[i]})$를 계산해보면 다음과 같다.

\[1.994,\ 2.025,\ 2.035,\ 2.039,\ 1.940,\ 2.032,\ 1.893,\ 2.011 \\ 1.903,\ 1.895,\ 1.881,\ 2.009,\ 1.905,\ 1.848,\ 2.038,\ 2.039\]

이제 $ps_i(X)=n\phi_n(X)-(n-1)\phi_{n-1}(X_{[i]})$를 계산해보면 아래와 같다.

\[1.605,\ 1.151,\ 0.998,\ 0.942,\ 2.416,\ 1.043,\ 3.122,\ 1.362\\ 2.972,\ 3.097,\ 3.308,\ 1.393,\ 2.951,\ 3.806,\ 0.958,\ 0.937\]

$ps_i(X)$의 평균과 분산을 계산하면,

\[ps(X)=2.00389\] \[V_{ps}(X)=1.0909\]

이므로 95% 신뢰구간은 $(1.4920, 2.5156)$이 된다. 실제로 이 16개 데이터들은 분산이 5.0인 분포로부터 추출한 것이고 $\log(5.0)=1.609$이므로 신뢰구간 안에 true parameter가 들어있는 케이스가 된다고 할 수 있다.

부트스트랩 방법

부트스트랩(bootstrap) 방법은 잭나이프 방법을 약간 변형한 것으로 1979년에 Bradley Efron이라는 사람이 고안해낸 방법이다.

부트스트랩이라는 말은 ‘자기 스스로 하는’, ‘독력(獨力)의’라는 뜻을 가진 단어이다.

다시 말해 주변의 도움 없이 스스로 해낸다는 의미인데, 컴퓨터의 부팅이 bootstrapping을 줄인 말이라는 것은 잘 알려져있는 사실이기도 하다.

영단어 bootstrap의 어원은 부츠 신발의 등쪽에 달려있는 끈을 얘기하는데, $\lt$허풍선이 남작의 모험$\gt$에 나오는 일화에서 남작이 늪에 빠졌을 때 부츠 등의 끈을 잡고 스스로 빠져나왔다는 어처구니 없는 이야기에서 유래됐다는 설이 있다.

(그런데 대부분의 판본에서는 머리카락을 잡고 늪에서 나왔다는 판본이 더 많다고 한다.)

그림 4. bootstrap의 물리적인 의미

아무튼간에 bootstrap이 왜 이런 이름을 갖게 되었는지 정도에 대해서만 알고 넘어가면 충분할 듯 싶다.

그림 5. 늪에서 빠져나오는 남작. bootstrap을 끌고 나왔다는 판본과 머리카락을 잡고 늪에서 빠져나왔다는 판본이 있다고 한다.

개요

부트스트랩은 잭나이프 방법과 유사하게 추정량(estimator)의 오차 범위를 파악하기 위해 사용되는 기법이라고 할 수 있다.

이를 위해 부트스트랩은 잭나이프 방법과 유사하게 resampling을 수행하는데, 잭나이프 방법과 다른 점은 중복을 허용한 resample을 수행한다는 점이다.

유일한 차이는 중복을 허용해줄 것인가 아닌가에 있는 것이기 때문에 아주 사소한 차이가 있을 것으로 보이지만, 결국에는 resample 가능한 경우의 수가 훨씬 늘어나게 되어서

resample된 샘플의 수는 더 많아지므로 resample된 sample의 histogram을 확인할 때 좀 더 부드러운 histogram을 볼 수가 있다.

다만, 컴퓨터의 도움 없이는 수 많은 경우의 수에 대해 대처하기 어려우므로 컴퓨터 성능의 발전과 함께 고안되고 실용적으로 사용되고 있는 방법이라고 할 수 있겠다.

부트스트랩 방법의 사용법

부트스트랩의 사용법은 잭나이프와 거의 유사한데, 기본적으로 resample을 통해 estimator의 오차 범위를 확인한다는 점은 같다.

다만, 두 가지 부분에서 차이를 보이는데, 하나는 resample시 반복 추출을 허용한다는 점이고, 또 다른 하나는 부트스트랩은 pseudo value 같은 것은 쓰지 않고 추출된 데이터를 그대로 estimator에 넣어 사용한다는 점이다.

조금 더 시각적으로 설명해보자면 다음과 같다.

아래의 그림과 같은 7개의 sample이 주어져 있다고 해보자. (동그라미 위의 숫자는 sample의 순번이다.)

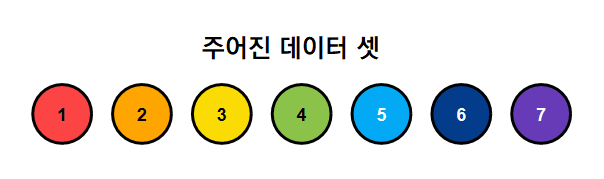
그림 6. 부트스트랩의 사용법을 설명하기 위해 생각해본 주어진 7개의 데이터 샘플

여기서 이렇게 주어진 7개의 데이터에 대해 반복 추출을 허용해가면서 랜덤하게 데이터를 resample한다고 해보자.

가령, 아래 그림 7과 같은 결과를 얻을 수 있을 것이다.

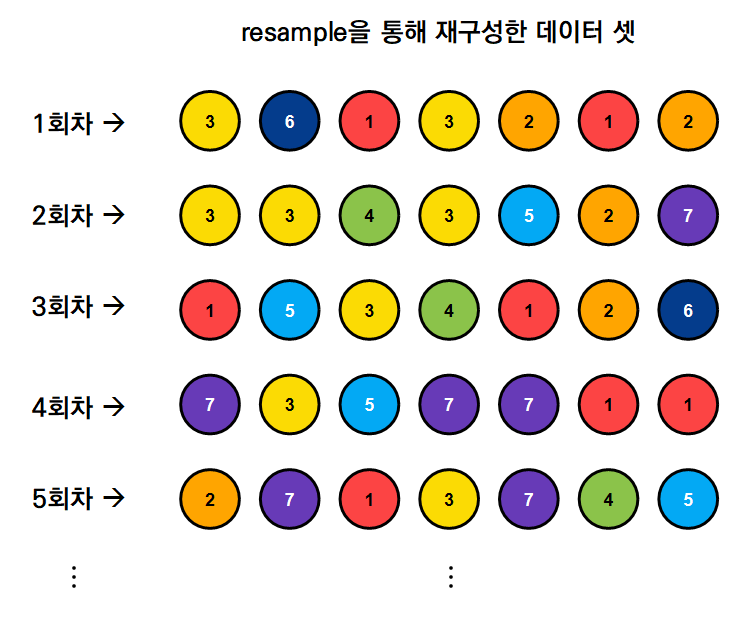
그림 7. 부트스트랩의 사용법을 설명하기 위해 생각해본 주어진 7개의 데이터 샘플

그림 7에서는 5회차까지만 resample하였지만, 1000회차, 혹은 5000회차까지 resample을 수행해보면 1000개 혹은 5000개의 데이터셋을 얻을 수 있게 된다.

이렇게 얻은 무수히 많은 데이터셋에 대해서 각각의 회차별로 estimator 값을 구하고 histogram을 구하면 estimator의 오차범위를 추정할 수 있게 되는 것이다.

부트스트랩의 사용 예시

우리는 잭나이프의 예시 문제에서 사용한 데이터셋과 estimator를 그대로 다시 활용해서 부트스트랩 방법으로 오차 범위를 생각해보려고 한다.

식 (8)과 (9)에 나와 있는 데이터셋과 estimator를 그대로 이용해보자.

우선 식 (8)에 있는 16개의 데이터셋에 대해 5000번의 중복을 허용한 resampling을 통해 데이터셋을 모은 뒤, 식 (9)에 있는 estimator를 적용시켜 5000개의 estimator value를 histogram에 뿌려보자.

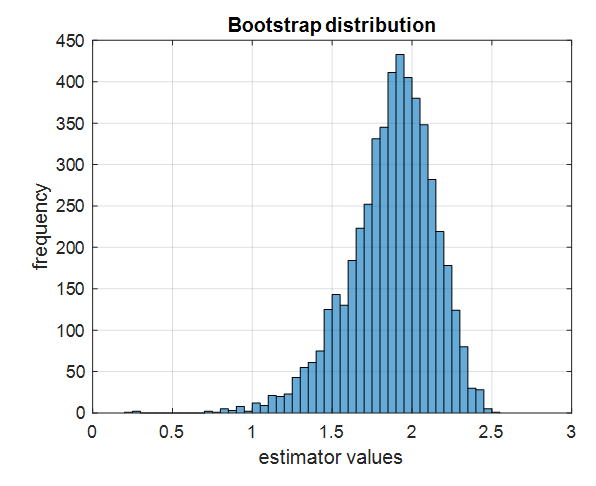
그림 8. 5000개의 부트스트랩 데이터셋에 estimator를 적용시켜 얻은 값들에 대해 histogram을 그려본 것

여기서 5000개 estimator 값들을 줄세워 상위 2.5% 값과 상위 97.5%의 값을 찾고 표시해보자. 그리고 식 (8)에 있는 데이터셋은 분산이 5인 데이터로부터 얻어졌으므로 true estimator value는

\[\log(5)=1.6094\]

임을 알 수 있으므로 true estimator value도 표시해보자. 그렇게 해주면 아래 그림과 같다.

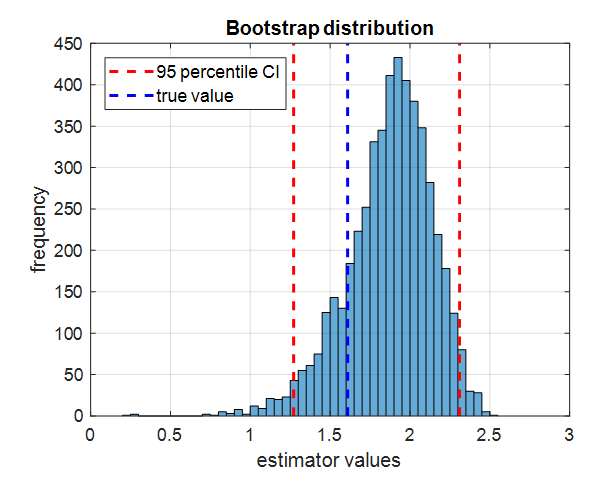
그림 9. 부트스트랩 데이터셋에 estimator를 취해 얻은 값들의 상위 2.5 percentile 값과 상위 97.5 percentile 값, 그리고 true value를 표시한 것

이렇게 얻은 상위 2.5 percentile과 상위 97.5 percentile 값은 95% confidence interval이 된다.

이 방법은 percentile Confidence Interval이라고 불리는 방법인데, 이 방법이 가장 직관적으로 이해하기 쉽다.

물론 bootstrap 방법 이용 시 confidence interval을 계산하는 다른 방법들도 있으니 참고 문헌 중 (Singh and Xie)를 참고하도록 하자.

여하튼 여기서 주목해야 할 부분은 true value가 이 95% confidence interval 안에 속할 수 있게 된다는 점이다.

부트스트랩의 의의

부트스트랩은 결국 우리가 샘플링을 여러번 하지 못하는 현실에서 여러번 추출할 수 있었을 샘플의 estimator 값 분포가 어땠을지를 논리적으로 추정할 수 있게 해준다는데 의의가 있다.

이 내용은 표본과 표준 오차의 의미 편에서 다룬 내용과 궤를 같이 하는 것인데,

평균(mean)같이 표준 오차가 잘 알려진 estimator들은 이런 부트스트랩 같은 방법을 쓸 하등의 이유가 없지만 표준 오차를 계산하는 방법이 잘 알려져 있지 않은 식 (9)와 같은 estimator들은

부트스트랩 방법을 통해 손쉽게 오차 범위를 생각해볼 수 있게 해주는 것이다.

참고문헌

• Jackknife resampling, Wikipedia
• Resampling data: using a statistical jackknife, S. Sawyer, Washington University, 2005
• Bootstrap: A statistical Method, Kesar Singh and Minge Xie, Rutgers University