Prerequisites
비제차 미분방정식의 의미에 대해 더 잘 알기 위해서는 아래의 내용에 대해 알고 오시는 것이 좋습니다.
1계 비제차 미분방정식
1계 선형 미분방정식의 형태는 다음과 같았다.
\[\frac{dx}{dt}+p(t)x = q(t) % 식 (1)\]만약 여기서 $q(t)=0$인 경우를 우리는 제차 혹은 동차 미분방정식(homogeneous DE)이라고 부르고, $q(t)\neq 0$인 경우를 비제차 혹은 비동차 미분방정식(nonhomogeneous DE)이라고 부른다.
(여기서 DE는 Differential Equation을 줄인 말이다. 또, 이 article에서는 한국어 표현 중에서는 제차, 비제차의 용어를 사용할 것이다.)
그런데, 우리는 미분방정식에 대해 공부할 때 1계 비제차 미분방정식에 대해서는 크게 다루지 않는다.
왜냐하면 1계 비제차 미분방정식은 해를 구하는 것이 어렵지 않기 때문이다.
1계 선형 미분방정식의 해법 편에서 배운바와 같이 식 (1)과 같은 1계 비제차 미분방정식의 솔루션은 아래와 같다.
식 (1)의 $p(t)$에 대해 다음과 $\int p(t)dt = \mu(t)$와 같은 관계를 갖는 $\mu(t)$를 생각해볼 때,
\[x(t) = \frac{1}{e^{\mu(t)}}\left(\int e^{\mu(t)}q(t)dt + C\right) % 식 (2)\]이다.
하지만, 제차 미분방정식과 비제차 미분방정식에 대해 배울 때 솔루션을 구하는 방법에 대해서만 너무 몰두하다보면 비제차 미분방정식이 갖는 의미에 대해서는 정작 이해하지 못할 수가 있다.
비제차 미분방정식은 독립변수에만 의존적인 값이 $x$의 변화율에 추가된다는 관점에서 제차미분방정식과 다르다.
예를 들어, 아래와 같은 미분방정식은 제차 미분방정식이다.
\[\frac{dx}{dt} = x % 식 (3)\]그런데, 어떤 미분방정식은 $x(t)$의 변화율 $dx/dt$가 독립변수 $t$에 따라 추가로 변할 수 있기 때문에 아래와 같은 형식으로도 표현될 수 있다.
\[\frac{dx}{dt} = x+e^{t/2} % 식 (4)\]식 (3), (4)에 해당되는 방향장과 솔루션 커브 몇 가지를 그리자면 아래의 그림 1과 같다.
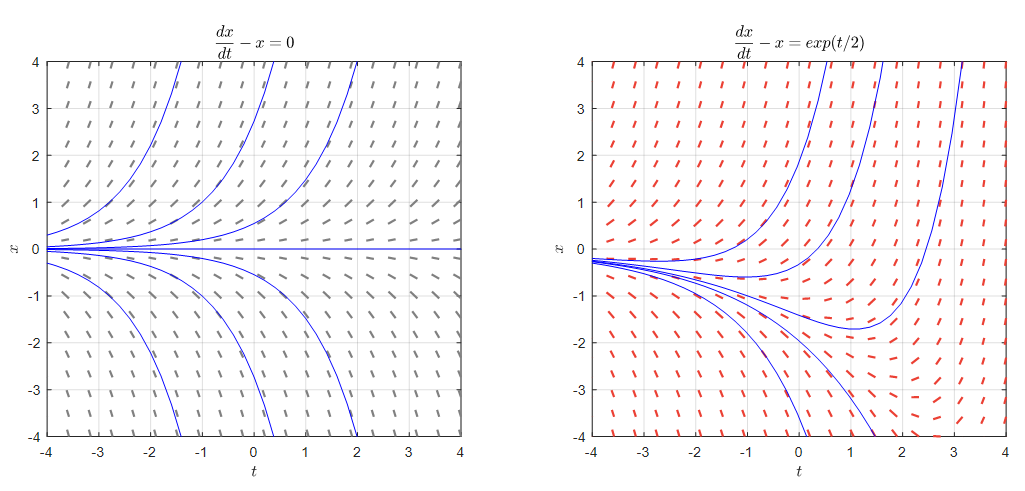
그림 1. 제차/비제차 미분방정식(각각 식 (3), (4))의 방향장 비교
그림 1의 두 방향장의 slope들을 보면 독립변수 $t$가 0보다 작은 경우에는 왼쪽 오른쪽 그림의 방향장의 형태가 크게 다르지 않아 보이지만, $t$가 커질 수록 방향장의 형태가 많이 바뀌게 된다는 것을 알 수 있다.
그 이유는 식 (4)에 있는 $\exp(t/2)$ 함수는 독립변수 $t$가 커짐에 따라 값이 더 커지기 때문이며 그에 따라 기울기 값이 더 크게 변하게 되기 때문이다.
식 (1)을 가지고 다시 보면, 비제차 미분방정식은 원래의 제차방정식의 형태
\[\frac{dx}{dt}+p(t)x = 0 % 식 (5)\]의 우변에 $q(t)$를 더해둔 것과 같은 모습이다. 다시 말해 기존의 제차 미분방정식이 갖고 있던 방향장의 형태에 $t$에만 의존적인 변화가 추가된다는 것이다.
이것을 그림으로 표현하면 아래의 그림 2와 같다.
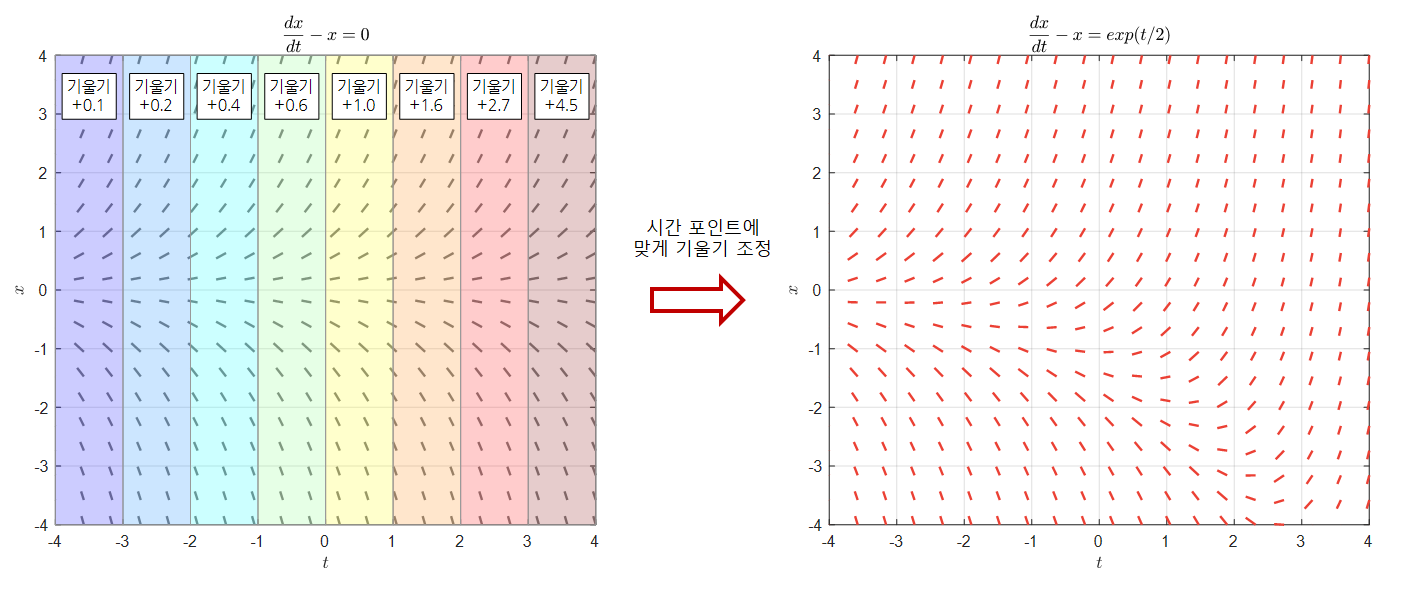
그림 2. 비제차 방정식의 방향장은 독립 변수의 구간 별로 비제차 항(식 (1)의 $q(t)$)의 값을 기울기에 더해준 것이다.
연립 비제차 미분방정식
이번에는 미분방정식의 식이 두 개 이상인 경우에 해당하는 연립 미분방정식에 대해 생각해보자.
연립 미분방정식 모델링 편에서는 아래와 같은 두 개의 종속변수에 대한 변화를 동시에 모델링 할 수 있는 제차 연립미분방정식을 소개한 적 있다.
\[\begin{cases}\dfrac{dx}{dt} = f(x,y) \\\\ \dfrac{dy}{dt}=g(x,y)\end{cases} % 식 (6)\]연립 미분방정식을 비제차 형식으로 만들게 된다면 아래와 같은 꼴을 띄게 된다.
\[\begin{cases}\dfrac{dx}{dt} = f(x,y) + p(t)\\\\ \dfrac{dy}{dt}=g(x,y) + q(t)\end{cases} % 식 (7)\]연립 비제차 미분방정식은 독립변수에만 의존적인 값이 $x$ 혹은 $y$의 변화율에 추가된다는 점이 1계 비제차 미분방정식과 동일하다.
그런데, 연립 비제차 미분방정식을 그리려고 하니 하나의 문제가 있다. 가령, 종속변수가 $x, y$로 두 개인 연립 비제차 미분방정식이라고 하면 이 미분방정식의 해를 시각화 하기 위한 위상 평면의 가로축, 세로축에는 모두 종속변수가 들어가지 독립변수 $t$가 들어갈 자리는 없기 때문이다.
첫 번재 방법은 3차원 plot을 그리는 것이다. 즉, 독립변수에 축(axis)을 하나 할당해주고, 독립변수의 변화에 따른 phase plane을 그려나가는 것이다.
하지만, 이런 방법으로는 시각화를 한들 눈으로 보고 이 변화를 이해하기 어렵다.
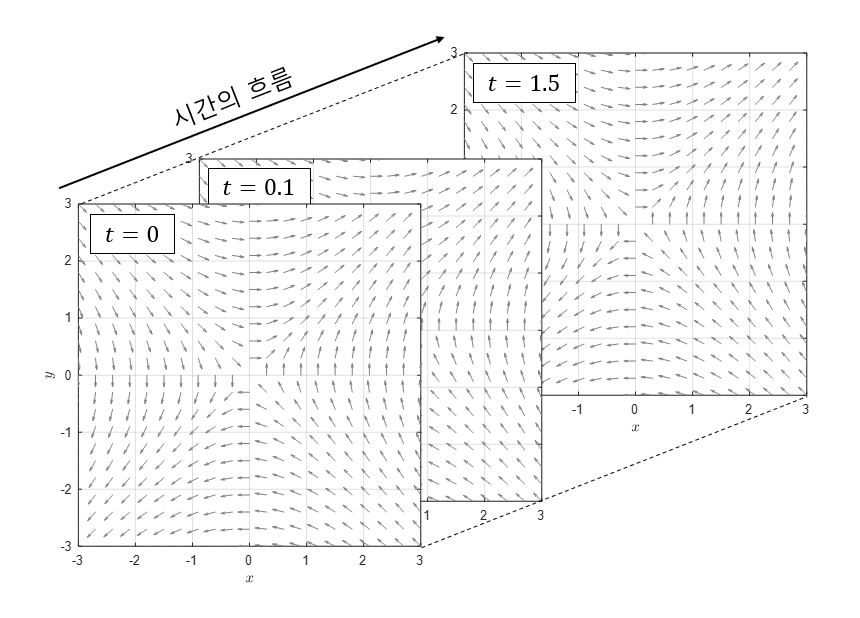
그림 3. 시간 축을 추가해 3차원으로 구성해본 위상평면의 형태. 시각적으로 단번에 변화를 이해하기는 어렵다.
두 번째 방법은 애니메이션을 만드는 것이다. 다시 말하면, 독립변수를 시간(time)으로 해석해 시간의 변화에 따른 phase plane의 변화를 매 순간 순간 마다 그리는 것이다.
다시 말하면 애니메이션이다.
우리는 두 번째 방법을 이용해 연립 비제차 미분방정식의 해의 특성을 파악할 것이다.
예를 들어 아래와 같은 2원 1계 연립 비제차 미분방정식이 있다고 생각해보자.
\[\begin{cases}\dfrac{dx}{dt} = y + \cos(t)\\\\ \dfrac{dy}{dt}=x+\sin(t) \end{cases} % 식 (8)\]위 식의 제차 미분방정식 형태에서는 $\cos(t)$ 혹은 $\sin(t)$의 term 이 없었을 것이고 phase plane은 아래와 같을 것이다.
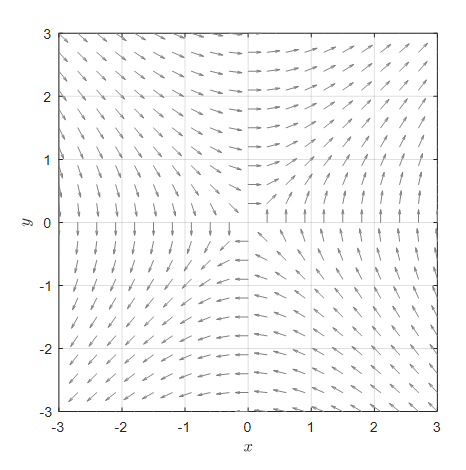
그림 4. 식 (8)의 제차 방정식 형태를 phase plane에 표시한 것
이제, $\cos(t)$ 혹은 $\sin(t)$라는 시간-의존적인(time dependent) term을 넣어 $t$값에 따라 phase plane이 달라지도록 그리면 다음과 같다.
그림 5. 식 (8)의 시간 $t$에 따른 phase plane의 변화
phase plane이 시간에 따라 바뀐다는 것은 initial condition에 따라 나오는 curve도 시시각각 따라가는 방향이 바뀐다는 것을 의미한다. 아래의 그림 6에서는 그러한 내용을 표현하였다.
그림 6. 여러가지 initial condition에 따른 solution curve의 변화
이 중 가령 (2, -3)에서 시작하는 경우의 solution curve는 아래의 영상과 같이 그려지게 된다.
그림 7. 특정 initial condition에 따른 solution curve
General solution = homogeneous + particular solution 인 이유
학부 시절 미분방정식을 배울 때 제일 이해되지 않았던 개념 중 하나가 일반해(general solution)에 대한 개념이었다.
미분방정식의 일반해는 homogeneous solution과 particular solution을 합친 것이라는 것이다.
예를 들어,
\[x''-4x'+3x=t % 식 (9)\]라는 미분방정식을 풀면 그 일반해는
\[x(t) = x_h(t) + x_p(t) = \left(c_1 e^t + c_2 e^{3t}\right) + \left(\frac{t}{3} + \frac{4}{9}\right) % 식 (10)\]와 같은데, (이 해를 구하는 구체적인 방법에 대해서는 추후 설명할 예정이다.)
앞의
\[x_h(t) = c_1 e^t + c_2 e^{3t} % 식 (11)\]은
\[x''-4x'+3x=0 % 식 (12)\]이라는 식을 풀어서 얻어내는 결과물이고, 뒤의
\[x_p(t) = \frac{t}{3}+\frac{4}{9} % 식 (13)\]는 식 (9)만을 풀어서 얻어낸 결과물이다.
(다시 말해 $x_p(t)$를 원래의 비제차 미분방정식에 대입하면 성립한다.)
식 (11)과 식 (13)의 두 결과물들을 각각 homogeneous solution, particular solution이라고 부른다.
얼핏 생각하면 일반해는 식 (13)의 $x_p(t)$ 하나만으로도 충분할 것 같지만, 실제로는 $x(t) = x_h(t)+x_p(t)$이다.
그 이유는 잘 생각해보면 그림 1 혹은 그림 4에서 알 수 있는데, 비제차 미분방정식의 해는 원래의 제차미분방정식 꼴의 방향장 혹은 위상평면에 독립변수에 의존적인 함수로부터 얻어진 기울기의 변화가 더해진 것이기 때문이다.
심지어 그림 1 혹은 그림 5를 놓고 생각해보면 독립 변수에만 의존적인 비제차 term만으로는 기울기라는 것은 생각해볼 수도 없는 것이다.
따라서, 비제차 미분방정식의 완전한 솔루션은 제차미분방정식의 해와 비제차 term으로부터 얻게된 해를 더한 것으로 생각해야만 한다.