Prerequisites

해당 포스트에 대해 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 허수의 존재 의미에 대하여
• 자연상수 e의 의미
• 오일러 공식의 기하학적 의미
• 고윳값과 고유벡터의 기하학적 의미

회전 행렬의 고윳값과 고유벡터

\[A=\begin{bmatrix}\cos(\theta) && -\sin(\theta) \\ \sin(\theta) && \cos(\theta)\end{bmatrix}\]

가령 90도 시계반대방향으로 회전하는 행렬을 적용해 선형변환 한 결과는 다음과 같다.

\[\begin{bmatrix} \cos(\pi/2) & -\sin(\pi/2) \\ \sin(\pi/2) & \cos(\pi/2) \end{bmatrix}\]

그림 1. 시계반대방향으로 회전하는 선형변환의 시각화

고윳값과 고유벡터의 의미편에서 얘기했던 것의 핵심은 다음과 같았다.

“벡터 x에 어떠한 선형변환 A를 했을 때, 그 크기만 변하고 원래 벡터와 평행한 벡터 x는 무엇인가요?”

“그렇다면, 그 크기는 얼마만큼 변했나요?”

라는 얘기 말이다.

그렇다면 의문이다. 회전 변환 시 크기만 바뀌고 방향이 바뀌지 않는 벡터는 어디있는가?

고윳값과 고유벡터의 계산

회전 행렬의 고윳값과 고유벡터의 의미를 파악하기 위해 직접 고윳값과 고유벡터를 계산해보도록 하자.

고윳값의 계산

\[A\vec{x}=\lambda\vec{x}\] \[=\begin{bmatrix}\cos(\theta) && -\sin(\theta) \\ \sin(\theta) && \cos(\theta)\end{bmatrix}\vec{x} = \lambda\vec{x}\]

여기서 $\vec{x}$는 $I\vec{x}$로 분해해 생각할 수도 있으므로,

여기서 $I$는 아래와 같은 identity matrix이다.

\[I=\begin{bmatrix}1 && 0\\0 && 1\end{bmatrix}\] \[\Rightarrow \begin{bmatrix}\cos(\theta) && -\sin(\theta) \\ \sin(\theta) && \cos(\theta)\end{bmatrix}\vec{x} = \lambda I\vec{x}\]

여기서 우변을 좌변으로 옮겨 계산하면,

\[\Rightarrow (A-\lambda I)\vec{x} = \begin{bmatrix}\cos(\theta)-\lambda && -\sin(\theta) \\ \sin(\theta) && \cos(\theta)-\lambda\end{bmatrix}\vec{x}=\vec{0}\]

여기서 $\vec{X}$가 영벡터가 아니기 위해선 $(A-\lambda I)$가 역행렬을 가지지 않아야 하므로 $(A-\lambda I)$의 행렬식의 값은 0이 되어야 한다.

\[det(A-\lambda I)=(\cos(\theta)-\lambda)^2+\sin^2(\theta) = 0\] \[=\cos^2(\theta) - 2\lambda\cos(\theta) + \lambda^2 + \sin^2(\theta)=0\]

여기서 $\cos^2(\theta) + \sin^2(\theta) = 1$ 이므로,

\[\Rightarrow \lambda^2 -2\lambda\cos(\theta) + 1 = 0\]

2차 방정식에 대한 근의 공식을 적용하면 $\lambda$는 다음과 같이 계산할 수 있다.

\[\lambda = \cos(\theta) \pm\sqrt{\cos^2(\theta)-1}\] \[=\cos(\theta)\pm\sqrt{-\sin^2(\theta)}\] \[=\cos(\theta) \pm i\sin(\theta)\]

여기서 $i=\sqrt{-1}$이다.

이제, 각 eigenvalue에 대응되는 eigenvector를 계산해보자.

1. $\lambda=\cos(\theta)+i\sin(\theta)$인 경우의 고유벡터

$\lambda = \cos(\theta) + i\sin(\theta)$ 인 경우,

\[\begin{bmatrix}\cos(\theta) && -\sin(\theta) \\ \sin(\theta) && \cos(\theta)\end{bmatrix}\vec{x} = (\cos(\theta) +i\sin(\theta))\vec{x}\]

을 만족해야 한다.

우변을 좌변으로 넘기면,

\[\Rightarrow \begin{bmatrix}-i\sin(\theta) && -\sin(\theta) \\ \sin(\theta) && -i\sin(\theta)\end{bmatrix}\vec{x}=0\]

즉, 위의 행렬과 벡터의 곱은 아래의 선형연립방정식을 푸는 것과 같다고 할 수 있다.

벡터 $\vec{x} = \begin{bmatrix}x_1, x_2\end{bmatrix}^T$라고 하면,

\[\begin{cases} -i\sin(\theta) x_1 - \sin(\theta)x_2 =0 \\ \sin(\theta)x_1 - i\sin(\theta)x_2 =0 \end{cases}\]

이며,

여기서 모든 방정식을 $\sin(\theta)$로 나누면¹,

\[\begin{cases} -i x_1 - x_2 =0 \\ x_1 - i x_2 =0 \end{cases}\]

이므로,

\[\vec{x}=\begin{bmatrix}i\\1\end{bmatrix}\]

이다.

2. $\lambda=\cos(\theta)-i\sin(\theta)$인 경우의 고유벡터

1에서와 비슷한 방법으로 고유벡터를 계산하면

$\lambda=\cos(\theta)-i\sin(\theta)$인 경우의 고유벡터는

\[\vec{x}=\begin{bmatrix}-i\\1\end{bmatrix}\]

이다.

고윳값과 고유벡터에 대한 또 다른 관점

다시 한번, 고윳값과 고유벡터의 기하학적 의미 편에서는 고윳값과 고유벡터를 다음과 같이 생각하자고 하였다.

“벡터 x에 어떠한 선형변환 A를 했을 때, 그 크기만 변하고 원래 벡터와 평행한 벡터 x는 무엇인가요?”

“그렇다면, 그 크기는 얼마만큼 변했나요?”

즉, 위의 관점은 어떤 선형변환에 대해 고윳값과 고유벡터를 찾는 과정에 초점을 맞춘 것이라고 볼 수 있겠다.

하지만, 이렇게도 한번 생각해보자. 우리가 적절한 고윳값과 고유벡터를 안다고 하면, 해당 고유벡터에 대해선 고윳값이 가지는 의미는 다음과 같다.

"고유벡터에 대한 선형변환은 딱 고윳값 만큼만 상수배 해주게 된다."

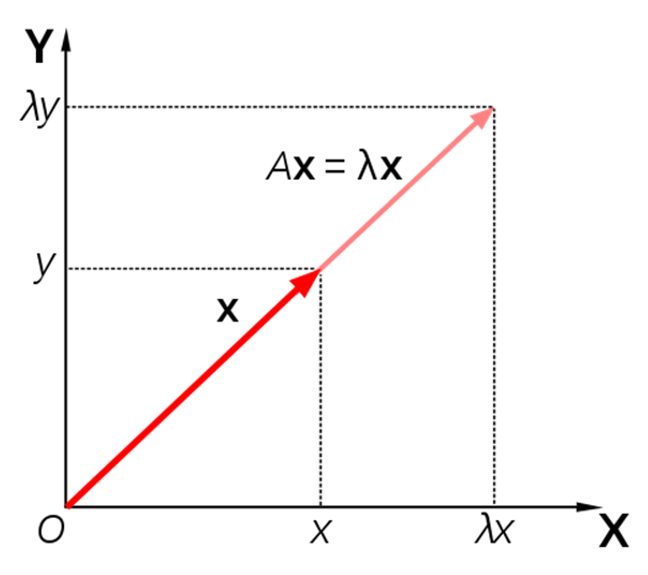
그림 2. 고유벡터에 선형변환이 작용되면 딱 고윳값 만큼만 상수배 해주게 된다.

상수배란 무엇일까?

상수배란 벡터의 기본 연산(상수배, 덧셈) 편에서 다룬 것과 같이 벡터로써 갖추어야 할 기본적인 성질이다.

하지만, 그 근본적인 의미는 ‘곱셈’에 있다고 할 수 있다.

허수의 존재 의미 편에서 언급했던 것 처럼 곱셈은 방향성을 갖는다.

음수를 곱한다는 것은 반대 방향으로의 변환을 의미하고, 복소수를 곱한다는 것은 ‘회전’을 의미한다.

그림 3. 복소수(여기선 순 허수)를 곱한다는 것의 기하학적 의미

또, 오일러 공식의 기하학적 의미편에서는

\[\exp(i\theta) = \cos(\theta) + i \sin(\theta)\]

라는 복소수가 가지는 의미는 1이라는 숫자를 복소평면 상에서 $\theta$ 라디안 만큼 회전시켜준 것임을 알아보았었다.

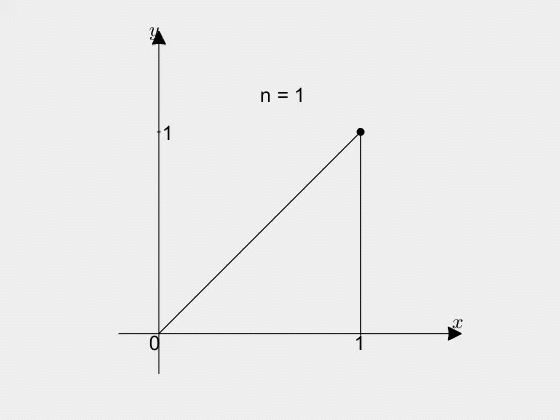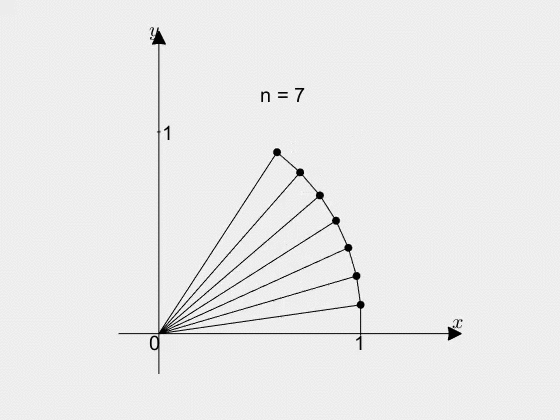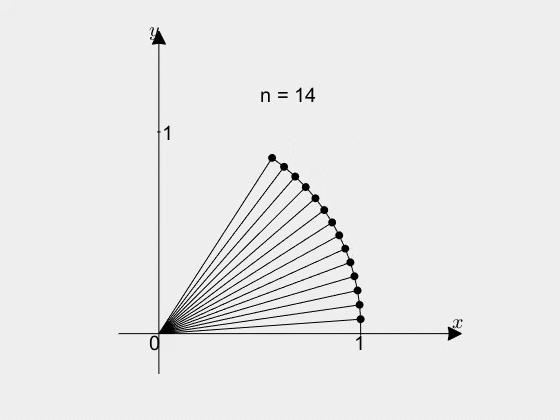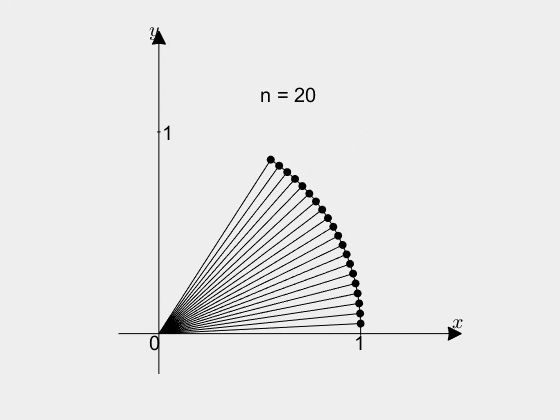
그림 4. 오일러 공식의 기하학적 의미를 알아가는 과정. n의 값이 커질 수록 복소 평면 상의 $\cos(\theta)$, $\sin(\theta)$라는 점으로 변환 후의 점이 이동한다. 좀 더 자세한 내용은 오일러 공식의 기하학적 의미 편을 참고할 것

결국, 복소 고윳값이 가지는 의미는 벡터의 길이가 줄어들거나 늘어나는 것이 아닌 ‘복소수 곱셈을 통한 벡터의 회전’에 있는 것이다.

복소 고유벡터의 시각화

한편, 우리가 회전행렬에 대해 얻은 복소 고유벡터는 어떻게 생각해야할까?

복소 고유벡터를 시각적으로 표현하거나 이해하기 어려운 이유는 복소수 자체가 이미 2차원의 수이기 때문이다.

조금 더 풀어쓰자면 복소수는 “실수부”와 “허수부”에 들어갈 두 개의 숫자가 있다.

그래서 2차원 복소 벡터는 들어가야 할 실수(real number)가 총 네 개가 있게 되는데, 우리는 4차원의 세계를 이해할 방법이 없기 때문에 정확히 2차원 복소 벡터를 표현할 방법은 없다.

하지만, 필자는 필자 나름대로의 방법으로 우리가 얻은 2차원 복소 벡터 두 개를 시각화 해보고자 한다.

우리가 얻은 복소 벡터 두 개는 다음과 같았다.

\[v_1 = \begin{bmatrix} i \\ 1 \end{bmatrix}\] \[v_2 = \begin{bmatrix} -i \\ 1 \end{bmatrix}\]

각각의 복소벡터를 시각화 하면 다음과 같이 표현할 수 있을 것이다.

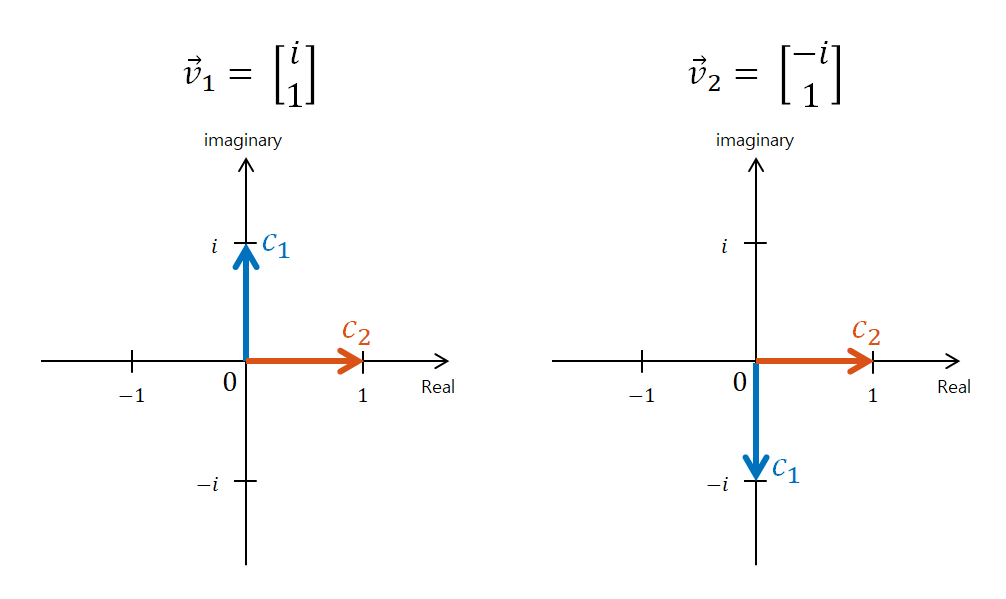
그림 5. 복소벡터 $v_1$과 $v_2$를 시각화 한 것. 그림 안에서 $c_1$과 $c_2$는 각각 각 벡터 내의 첫번째와 두 번째 원소들을 의미한다.

위 그림에서 가장 주목했으면 하는 부분은 $\vec{v}_1$과 $\vec{v}_2$가 두 개의 화살표로 표현되어 있지만 이 두 개의 화살표를 하나로 묶어 벡터로 보자는 것이다.

중요하다고 생각하기 때문에 다시 말하자면 두 개의 화살표가 하나의 복소 벡터를 표현하는 것이다.

회전 행렬과 고유벡터의 상호작용

그럼 이제, 아래의 문구에 대해 다시 한번 생각해보자.

"고유벡터에 대한 선형변환은 딱 고윳값 만큼만 상수배 해주게 된다."

그림 5에서 표현한 복소 벡터 $\vec{v}_1$과 $\vec{v}_2$에 대해 고윳값만큼 상수배 해준다는 것은 어떤 의미일까?

고윳값은 $\exp(i\theta)$와 $\exp(-i\theta)$이므로 반시계방향 혹은 시계방향으로의 $\theta$ 라디안 만큼의 회전을 의미한다.

즉, 그림 5에서 표현한 복소 벡터 $\vec{v}_1$과 $\vec{v}_2$에 대해 고윳값만큼 상수배 해준다는 것의 의미는 고유벡터를 반시계방향 혹은 시계방향으로 $\theta$ 라디안 만큼 회전시킨다는 의미를 갖는다.

아래의 그림 6과 7에서 두 개의 서로 다른 고윳값에 대해 슬라이더를 움직여가며 회전 행렬과 고유벡터의 상호작용에 대해 시각적으로 확인해보자.

\[A=\begin{bmatrix}\cos(\theta) && -\sin(\theta) \\ \sin(\theta) && \cos(\theta)\end{bmatrix}\]

그림 6. $\lambda_1 = \exp(i\theta)$인 경우의 회전행렬과 고유벡터의 상호작용. 우측 상단에 있는 흰색 호(arc)는 회전 각도에 해당.

그림 7. $\lambda_2 = \exp(-i\theta)$인 경우의 회전행렬과 고유벡터의 상호작용. 우측 상단에 있는 흰색 호(arc)는 회전 각도에 해당.

다시 말하지만, 그림 6과 7의 결과는 결국 벡터가 상수배 되는 것이 복소수의 수준에서는 이렇게 표현될 수 있다는 것을 보여주는 것이다.

특히, 여기서는 고윳값과 고유벡터라는 특수한 경우에 한해서 얘기하는 것이지만 말이다.

참고 자료

• Visualizing the eigenvectors of a rotation / Twisted Oak Studios