파라미터 n, p를 수정해가며 다양한 경우의 이항분포의 생김새에 대해 확인해보자.
이항분포에서 x 축에 있는 k가 갖는 것은 어떤 의미일까?
그리고 각 막대의 길이는 어떤 의미를 갖는지 설명할 수 있는가?

확률통계학을 처음 접할 때 가장 먼저 만나게 되는 예시는 동전 던지기이다.

일상 생활에서 쉽게 접할 수 있는 “명백한” 확률적인 이벤트이기 때문이다.

이항 분포는 동전 던지기의 “앞면” 혹은 “뒷면”과 같이 두 가지 사건만 일어날 수 있는 경우에 대해 기대해볼 수 있는 분포라고 할 수 있다.

즉, 쉬운 예시를 가지고 이해할 수 있는 좋은 확률분포라고 할 수 있다.

또, 이항 분포는 특정 조건을 만족하면 그 분포가 정규 분포에 근사하기 때문에 정규 분포를 이해할 수 있게 해주는 좋은 징검다리 역할을 수행하기도 한다.

아무쪼록 이항 분포는 처음 통계학을 접할 때 매우 중요한 역할을 하는 분포라고 할 수 있다.

그럼에도 불구하고 이항분포라는 말이 나오기만 하면 그게 뭐였는지, 매번 헷갈리기 일쑤다.

이항 분포의 정의부터 출발해 그 형태와 쓰임에 대해 다시 한번 생각해보도록 하자.

이항 분포의 정의

위키피디아에 따르면, 이항 분포(二項分布, binomial distribution)는 연속된 $n$번 독립적 시행에서 각 시행이 확률 $p$를 가질 때의 이산확률분포라고 정의하고 있다.

이항분포의 확률질량함수의 수식은 다음과 같이 정의되어 있다.

\[Pr(K=k) = % 확률에 대한 값이라는 뜻. \binom n k % binomial n k p^k(1-p)^{n-k} % k번 성공, (n-k)번 실패\]

여기서 $k=0, 1, 2, \cdots, n$이고

\[\binom n k=\frac{n!}{k!(n-k)!}\]

는 이항계수 ${}_n\mathrm{ C }_k$ 이다.

처음 이항분포의 식과 그 형태를 보면 가장 헷갈리는 것 중 하나는 과연 저 $k$라는 것이 무엇인지이다.

아래에서 예시를 통해 조금 더 자세하게 알아보겠지만 이항 분포를 볼 때 상상해야 하는 것은 특정 성공 확률($p$)을 갖는 이벤트를 $n$번 독립적으로 연속 수행하는 일이다.

이항 분포에서 확인하는 일은 $k$번의 성공$\left(p^k\right)$과 $n-k$번의 실패를 했을 확률$\left((1-p)^{n-k}\right)$이다. 이 때, 이항 분포는 $k$ 값이 0부터 $n$까지의 모든 경우의 수에 대한 확률을 조사해 각 경우에 대한 확률을 미리 계산해둔 것이라고 할 수 있다.

이 때, $n$회의 이벤트 중 성공 순서는 상관없이 $n$ 번 중 $k$번만 성공하면 되기 때문에 $\binom n k$라는 값이 각 $k$의 경우의 수에 대해서 곱해져 있는 것이다.

가령 세 번 중 두 번을 성공하는 케이스에 대해 생각한다고 하면,

(성공, 성공, 실패)

(성공, 실패, 성공)

(실패, 성공, 성공)

의 세 케이스 모두 3회 중 2회 성공, 1회 실패인 케이스로 볼 수 있다는 것이다.

이에 대해 조금 더 자세한 내용을 동전 던지기 예시를 통해 알아보자.

예시를 통한 이항 분포에 대한 이해

이항 분포의 정의가 말하는 것은 무엇일까? 예시를 통해 이 정의에 대해 조금 더 자세하게 알아보자.

가령, 동전을 10번 던졌을 때 앞면이 나올 횟수에 대해 알아보고 있다고 생각해보자.

동전을 던졌을 때 앞면이 나올 확률은 0.5 이다. 그러니, 10번 중 5번이 나올 확률이 제일 높을 것이다.

그런데, 10번 던졌을 때 4번 나올 수도 있지 않을까? 아마 5번 나올 확률 보다는 확률이 조금 낮겠지만 말이다.

혹시 운이 좋지 않아서 앞면이 3번만 나올 수도 있고, 앞면이 나오지 않을 수도 있지만 그럴 경우는 거의 없을 것이다.

즉, 이항분포는 $p$라는 확률(여기서는 0.5)을 가지는 사건을 연속 n회(여기서는 10회) 시행했을 때, $0$~$n$회 사이의 시행 중 우리가 원하는 사건이 몇 번 발생할 지를 확률적으로 기술해놓은 분포라고 할 수 있다.

이걸 확인해보려면 어떻게 해야할까?

첫 번째로는 $n, p, k$ 값을 직접 넣고 이항 분포를 계산하는 방법이 있을 수 있고 (선험적 확률), 또 한 가지 방법은 컴퓨터 시뮬레이션을 통해 확인해보는 방법(경험적 확률)이다.

이항 분포 직접 계산해서 그려보기 (선험적 확률)

동전 던지기를 10번 연속 시행하는 경우에 대해 이항 분포를 계산해보자.

우리는 $k = 0, 1, 2, \cdots, 10$과 같이 변한다는 것을 알고 있으므로 식 (1)을 이용해 가능한 모든 $k$에 대해 그 확률값을 계산할 수 있다.

\[k=0 :\frac{10!}{0!\cdot10!} \left(\frac{1}{2}\right)^0\cdot \left(1-\frac{1}{2}\right)^{10} = 0.0010\] \[k=1 :\frac{10!}{1!\cdot9!} \left(\frac{1}{2}\right)^1\cdot \left(1-\frac{1}{2}\right)^{9} = 0.0098\] \[k=2 :\frac{10!}{2!\cdot 8!}\left(\frac{1}{2}\right)^2\cdot \left(1-\frac{1}{2}\right)^{8} = 0.0439\] \[\vdots \notag\] \[k=10 :\frac{10!}{10!\cdot 0!}\left(\frac{1}{2}\right)^{10}\cdot \left(1-\frac{1}{2}\right)^{0} = 0.0010\]

11개의 모든 $k$ 값에 대한 계산 결과를 모아보면 다음과 같다.

\[Pr(K=k) = [0.0010, 0.0098, 0.0439, 0.1172, 0.2051, 0.2461, 0.2051, 0.1172, 0.0439, 0.0098, 0.0010]\]

숫자로만 보면 어려워 보일 수 있기 때문에 이 결과를 그림으로 그려보면 다음과 같다는 것을 쉽게 알 수 있다.

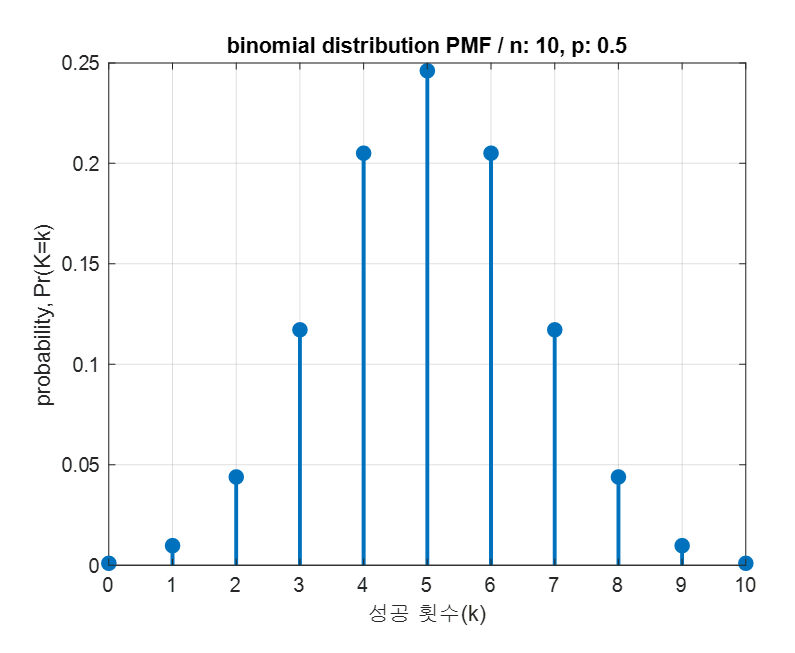
그림 1. 총 시행횟수 10, 성공확률 0.5인 경우의 다양한 성공 횟수에 대한 확률을 나타낸 이항분포의 형태

컴퓨터 시뮬레이션으로 이항분포 histogram 그리기 (경험적 확률)

두 번째 이항 분포의 모양을 확인해볼 수 있는 방법은 컴퓨터 시뮬레이션이다.

꼭 컴퓨터 시뮬레이션을 써야하냐고 물어본다면… 음 물론 직접 실험을 해볼 수도 있는 것이시지만 시간이 너무 많이 걸릴 수 있으므로 시뮬레이션을 수행해서 확인해보도록 하자.

시뮬레이션을 수행하는 방법은 간단하다.

$\quad$ 1. 0회 성공부터 10회 성공까지의 카운트 수를 모두 0으로 세팅해둔다.

$\quad$ 2. 10회 동전 던지기를 한다.

$\quad$ 3. 이 중 몇 번 앞면이 나왔는지(성공 횟수)를 세어본다

$\quad$ 4. 해당되는 성공회수의 성공 카운트를 올려준다. 가령 성공 횟수가 3이었다면 3회 성공의 카운트 수는 +1이 되는 것이다.

$\quad$ 5. 2~4을 무수히 많이 반복한다. (가령 100회 반복)

$\quad$ (물론 반복 회수는 많을 수록 선험적 확률 분포와 더 가까운 값을 얻을 수 있다.)

아래의 영상은 위의 1~5에서 소개한 시뮬레이션을 직접 수행해 카운트를 히스토그램 형태로 그려본 것이다.

그림 2. 시뮬레이션을 통해 획득한 이항 분포의 형태

이항 분포의 특성

이항 분포를 다루면서 알면 좋은 중요한 특성을 꼽아보자면 이항 분포의 평균, 분산값과 이항 분포가 어떤 조건에서 정규분포와 유사한 모습을 띄는지이다.

이항 분포의 평균과 분산

총 시행 횟수가 $n$, 성공 확률이 $p$인 이항 분포를 따르는 랜덤변수 $K$에 대해,

평균값은

\[E(K) = np\]

이고, 분산값은

\[Var(K) = np(1-p)\]

이다.

엄밀한 증명이라기 보단 상식적인 수준에서 생각해볼 수 있는 것은 사건을 $n$회 시행하고, 성공 확률이 $p$라면 평균적으로 $np$번 성공하는 것이 맞을 것 같다.

가령, 100회 동전을 던졌을 때 50번은 앞면이 나올 것이라고 보는 것이 상식적이다.

조금만 더 생각해보면, 평균값을 유도해볼 수 있는 방법으로는 기대값 연산의 선형성을 이용하는 방법이 있는데, $K$의 매 시행마다의 결과값을 다 더한 값이 마지막 $n$회 수행했을 때 획득되는 값이므로

\[K = K_1 + K_2 + \cdots + K_n\]

이라는 것을 알 수 있다. 따라서,

\[E[K] = E[K_1 + K_2 + \cdots + K_n] = E[K_1] + E[K_2] + \cdots + E[K_n]\]

매회 시행 시 기대값은 $p$와 같으므로,

\[\therefore E[K] = \sum_{i=0}^n E[K_i] = \sum_{i=0}^n p = np\]

라고도 볼 수 있다.

또, 분산의 정의는

\[Var(K) = \sum_i p_i(k_i-\mu)^2\]

이다. 이 때, 위에서 평균값을 얻어낸 것과 마찬가지로 $n$회의 각각의 시행에 대해서 생각해보면 결과$\left(k_i\right)$는 1 혹은 0 두가지 이고, 1이 나올 확률은 $p$, 0이 나올 확률은 $1-p$라는 것을 알 수 있다.

또, 한 번 시행했을 때의 기대값 $\mu= p$ 이므로 분산의 정의에 따라

\[\Rightarrow (1-p)(0-p)^2+p(1-p)^2 = p^2(1-p) + p(1-p)^2\] \[= p^2-p^3 + p(1-2p+p^2) = p^2 -2p^2 + p\] \[= p(1-p)\]

임을 알 수 있다.

따라서, $n$번 독립적으로 시행한 경우의 분산은 각 시행의 분산을 더해준 값과 같으므로,

\[\sigma_n^2 = \sum_{i=1}^n \sigma^2 = np(1-p)\]

이항분포의 정규분포 근사

본 포스팅의 맨 위에 있는 애플릿의 슬라이드들을 건드리다보면 이항 분포의 모습이 종모양(bell shape)의 정규분포의 형태와 유사한 형태를 띄는 경우를 볼 수 있다.

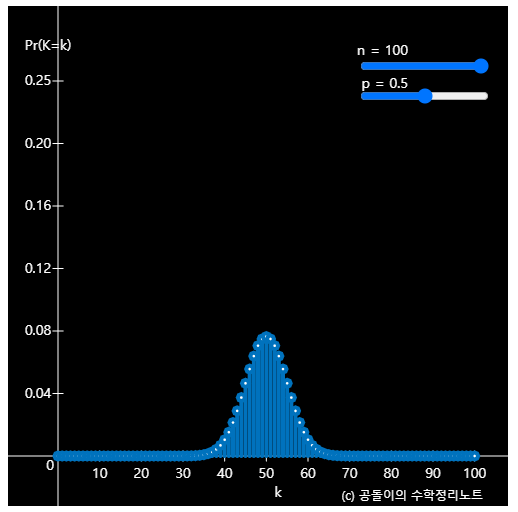
그림 3. 이항 분포의 형태가 정규분포와 유사한 경우

그런데, 어떤 경우에는, 가령 $n$이 너무 작거나 $p$가 너무 작거나 한 경우 이항 분포의 형태는 정규분포와 비슷하다고 말하기는 어렵다.

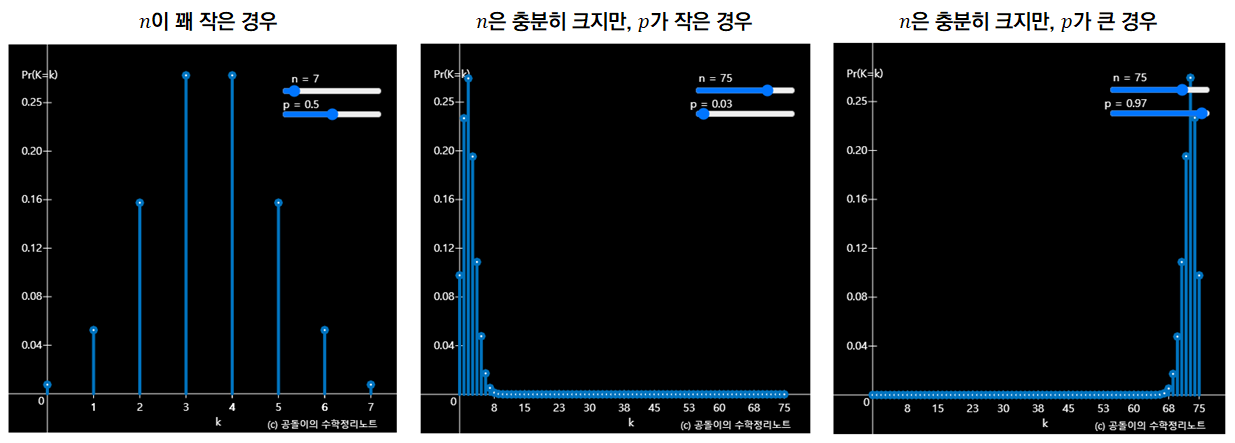
그림 4. 이항 분포의 형태가 정규분포와 유사하다고 보기 힘든 세 가지 경우

그림 4를 보면 $n$도 커야하지만 $p$도 어지간히 0.5 주변에 있어야만 정규분포의 모습을 따를 것이라는 것을 알 수 있다.

수학자들은 이항 분포가 정규분포의 형태와 유사해질 수 있다고 볼 수 있는 기준을 $np$와 $\sqrt{np(1-p)}$가 5보다 클 때로 보고 있고, 이 때 평균이 $np$이고 분산이 $np(1-p)$인 정규분포를 따른다고 볼 수 있다.