행렬식이 의미하는 것: 선형변환 될 때 단위 면적이 얼마만큼 늘어나는가?

※ 본 article에서는 열벡터(column vector) convention을 따릅니다.

행렬식

역행렬을 구할 때 사용되는 행렬식(determinant)는 $2\times 2$ 행렬에서 다음과 같이 정의된다.

DEFINITION 1. 행렬식
행렬 $$A=\begin{pmatrix}a& b \\ c & d \end{pmatrix}$$ 에 대하여 $$det(A) = ad-bc$$ 로 정의된다.

또, 역행렬은 다음과 같이 정의된다.

DEFINITION 2. 2 x 2 행렬의 역행렬
행렬 $$A=\begin{pmatrix} a& b \\ c & d \end{pmatrix} \notag$$ 에 대하여 $$A^{-1} = \frac{1}{det(A)} \begin{pmatrix}d& -b \\ -c & a \end{pmatrix}$$ 로 정의된다.

대수적으로 $AA^{-1} = A^{-1}A = I$는 라는 것을 보일 수는 있지만, 선형 대수학을 너머 행렬을 사용하는 수많은 수학 분야에서 행렬식은 등장한다. 특히 기하학에서 행렬식은 그 역할을 톡톡히 하는데 과연 행렬의 행렬식은 기하학적으로는 어떤 의미를 가지고 있는 것일까?

$2\times 2$ 행렬의 행렬식은 선형변환 후의 두 기저벡터가 이루고 있는 평행사변형의 넓이

[행렬과 선형변환]편에서 행렬을 이해하는 방법 중 하나로 행렬은 일종의 선형 변환이며 임의의 행렬

\[A=\begin{pmatrix} a& b \\ c & d \end{pmatrix}\notag\]

은 기저 벡터 $\hat{i} = (1,0), \space \hat{j} = (0,1)$을 새로운 기저벡터 $\hat{u} = (a,c), \space \hat{v} = (b,d)$로 바꿔주는 역할을 수행한다고 했다¹.

임의의 기저 벡터 $\vec{u}$와 $\vec{v}$는 좌표평면상에 그림 1과 같이 그려 표현할 수 있다.

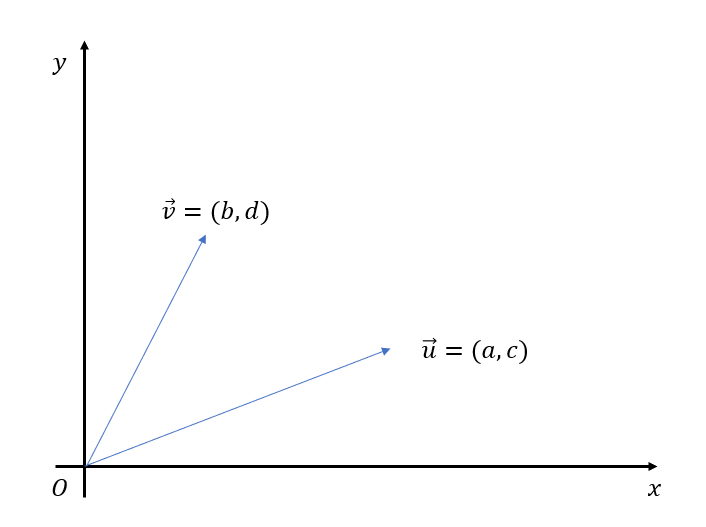
이 때, 그림 2에서 설명하듯 두 벡터를 통해 만든 평행사변형 AVOU의 넓이는 $det(A)$이다. 평행사변형 AVOU의 넓이는 삼각형 VOU의 넓이의 두배 값을 가진다. 그러므로 삼각형 VOU의 넓이를 구한 뒤, 두배를 해주면 평행사변형 AVOU의 넓이를 구할 수 있다.

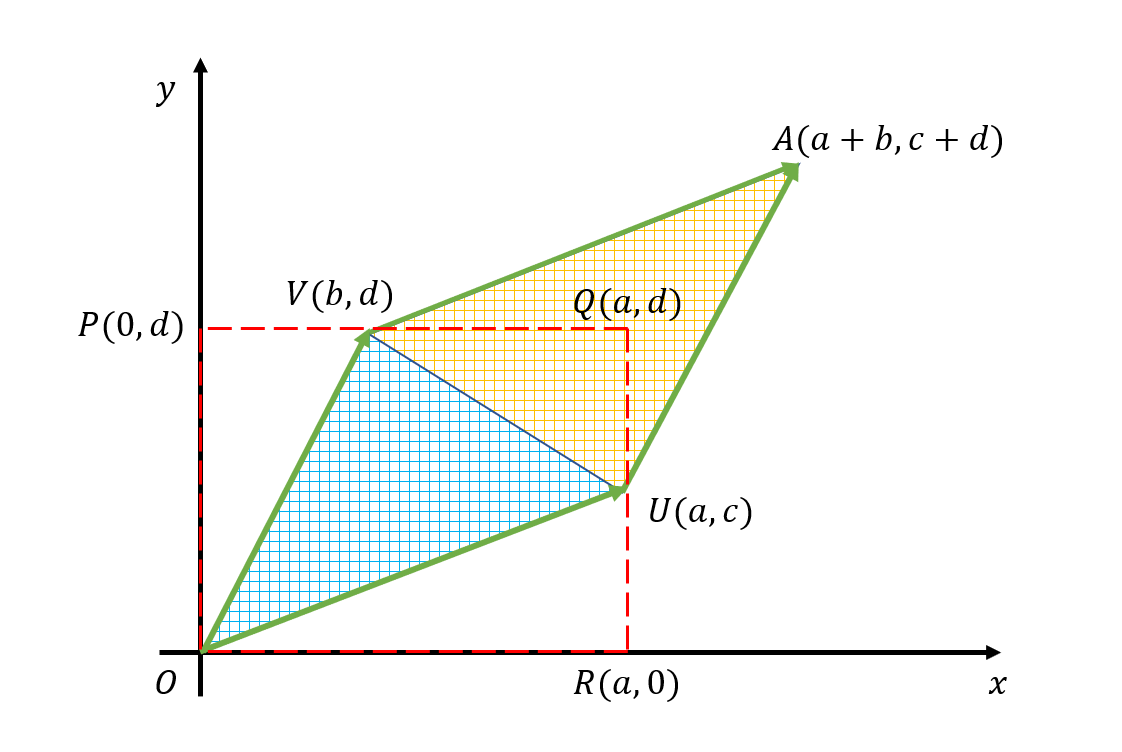
삼각형 VOU의 넓이는 사각형 PORQ에서 삼각형 POV, UOR, VUQ의 넓이를 빼준 빗금친 부분의 넓이와 같다. 그러므로,

\[◇AVOU = \notag\] \[=2\times\left\{□PORQ - △POV - △UOR - △VUQ\right\}\] \[=2\times \left\{ad-\frac{1}{2}bd -\frac{1}{2}ac - \frac{1}{2}(a-b)(d-c)\right\}\] \[=2\times\left\{ ad-\frac{1}{2}bd-\frac{1}{2}ac-\frac{1}{2}(ad-bd-ac+bc) \right\}\] \[=2\times\left\{ ad-\frac{1}{2}bd-\frac{1}{2}ac-\frac{1}{2}ad+\frac{1}{2}bd+\frac{1}{2}ac-\frac{1}{2}bc) \right\}\] \[=2\times\left\{ \left(ad-\frac{1}{2}ad\right) +\left(\frac{1}{2}bd-\frac{1}{2}bd\right) +\left(-\frac{1}{2}ac+\frac{1}{2}ac\right) -\frac{1}{2}bc) \right\}\] \[=2\times\left\{\frac{1}{2}ad-\frac{1}{2}bc\right\}\] \[=ad-bc = det(A)\]

행렬과 역행렬, 그리고 행렬식의 기하학적 관계

위 본문에서 행렬은 기하학적으로는 선형 변환을 의미한다고 하였다.

이러한 의미에서 역행렬도 하나의 행렬로 취급하는 것이기 때문에 역행렬 또한 기존의 행렬과 연관되어 있는 선형 변환을 의미한다.

기하학적으로 봤을 때, 역행렬은 원래 행렬을 이용한 선형변환의 역-선형변환이라고 할 수 있다. 다시 말하자면, 위 설명의 행렬을 통한 선형 변환은 한 변의 길이가 1인 정사각형을 넓이가 ad-bc인 평행사변형꼴로 바꾼 선형변환이며, 같은 행렬의 역행렬은 평행사변형 꼴로 바뀐 도형을 다시 한 변의 길이가 1인 정사각형으로 되돌려주는 역-선행변환이다.

그러므로, 역행렬에서는 $1/det(A)$라는 요소가 들어가게 되는 것이다.

마지막으로, 행렬식의 “ad-bc”라는 값을 시각적으로 확인할 수 있게하는 아주 좋은 애니메이션이 있어 첨부하고자 한다.

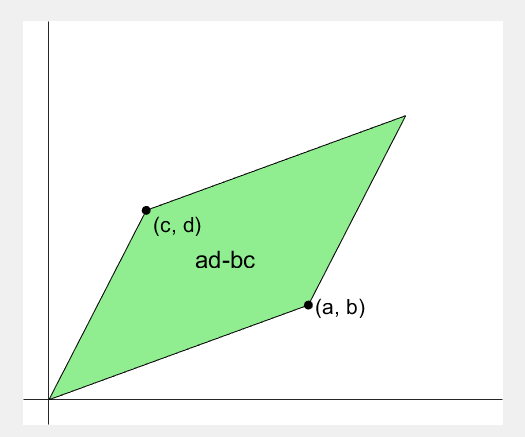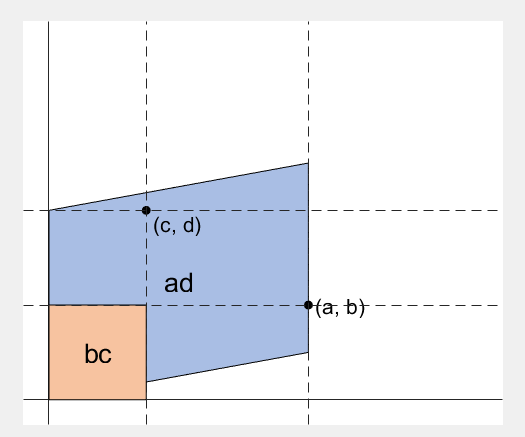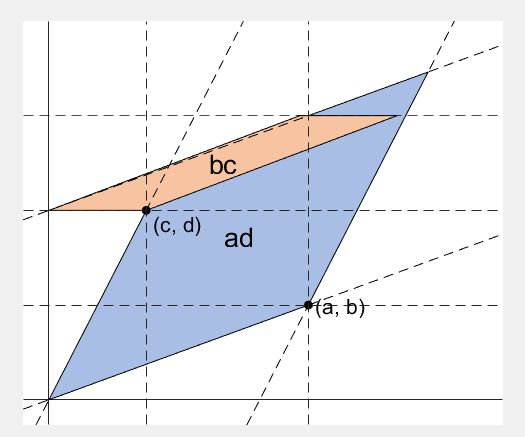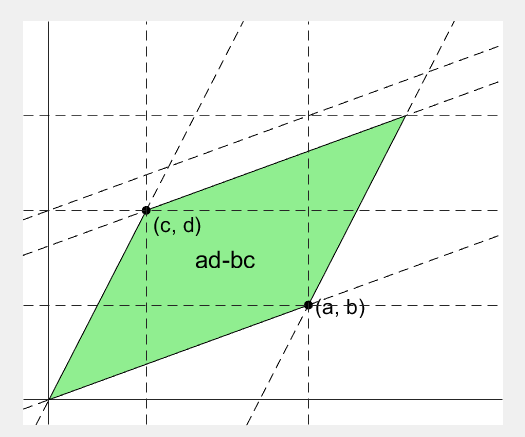
행렬식의 값은 왜 ad-bc?
원작자: 게으른맽랩( https://lazymatlab.tistory.com/201/)