본 포스팅은 IIT의 S. C. Duta Roy 교수님의 강의를 정리한 것임을 먼저 밝힙니다.
1. Analog Filter
가. 일반적인 아날로그 시스템과 필터
일반적인 아날로그 필터를 생각하는 데에 앞서 일반적인 아날로그 시스템의 모양은 어떻게 모델링되는지 아는 것은 매우 중요하다고 할 수 있다.
그것은 아날로그 시스템의 모양이 결국은 아날로그 필터를 구성하는 모양으로 귀결되기 때문이기도 하고, 이 포스트에서의 ‘일반적인 아날로그 신호 혹은 시스템’이란 것이 어떤 것으로 한정되어 있는지 미리 설정해놓고 가는 것 역시 중요하다고 여기기 때문이다.
이 포스트에서 생각하는 일반적인 아날로그 시스템은 선형 시불변 시스템을 의미한다. 그것은 외부의 noise가 없는 상당히 exactly determine되는 signal을 의미한다. 통상
\[x(t) \rightarrow h(t)\rightarrow y(t)\]로 표현되는 일반적인 LTI 모델은 다음과 같이 표현할 수도 있다.
\[y(k) = -\sum_{n=1}^{N}a_ny(k-n)+\sum_{n=0}^Nb_nx(k-n)\]이 때, impulse response를 통해서 시스템을 표현하면 다음과 같이 표현할 수도 있을 것이다.
\[Y(j\Omega) = H(j\Omega)X(j\Omega)\]이 때, $Y(j\Omega)$와 $X(j\Omega)$는 모두 다음과 같이 나타낼 수도 있을 것이다.
\[Y(j\Omega) = Y(s) = a_ns^n + a_{n-1}s^{n-1}+\cdots+a_1s^1 + a_0\] \[X(j\Omega) = X(s) = b_ns^n + b_{n-1}s^{n-1}+\cdots+b_1s^1 + a_0\]그러므로, 일반적인 시스템 $H(j\Omega)$는 다음과 같이 표현할 수도 있다.
\[H(s) \frac{\sum_{i=0}^{q}b_is^{-i}}{\sum_{k=0}^{p}a_ks^{-k}}\]한편, 필터 역시도 일종의 시스템이라고 생각할 수 있다. 그것은 시스템의 역할과 필터의 역할에 대해서, 특별하게 조작시킨 시스템은 필터의 기능을 수행할 수 있기 때문이다. 필터의 역할 또는 기능에 대해서 생각해보면, 그것은 원하는 정보를 증폭시키거나, 유지시키면서, 원치 않는 정보에 대해서는 감쇄 또는 제거하는 역할을 하는 것이라고 할 수 있는데, 적절히 조작된 시스템은 필터로 사용할 수 있기 때문이다. 그러므로 일반적인 아날로그 필터를 다음과 같이 정의할 수 있다.
\[H_a(s) = G\frac{1+d_1s^{-1}+\cdots d_qs^{-q}}{1+c_1s^{-1}+\cdots+c_qs^{-q}}\]통상 이런 종류의 Analog filter를 IIR 필터라고 한다.
다시 한번 말하자면, $H_a(s)$의 계수를 적절하게 조절해주면, $H_a(s)$를 필터로써 그 기능을 수행하게 해줄 수 있다. 많은 연구를 통해서 여러 형태의 필터가 고안되었는데, 그 중 가장 많이 쓰이는 IIR 필터는 Butterworth filter와 Chebyshev filter라고 할 수 있다.
Butterworth filter의 일반식은 다음과 같다.
\[|H_a(j\Omega)|^2 = 1 / \left\lbrace 1+\left(\frac{\Omega}{\Omega_c}\right)^{2N}\right\rbrace\]Chebyshev filter의 일반식은 다음과 같다.
\[|H_a(j\Omega)|^2 = 1/ \left\lbrace1+\epsilon^2C^2_N\left(\frac{\Omega}{\Omega_p}\right)\right\rbrace\]먼저, life를 simple하게 만들어주는 Butterworth filter에 대해서 알아보자.
2. All-pole filters
Butterworth filter의 식을 잘 보자. 일반적인 Filter의 모양에 비해서 많이 다르다는 것을 알 수 있다. 그것의 첫 번째 시작은 일반적인 filter 모델의 식에서 분자 부분의 요소들이 모두 사라지고 1만 남아있다는 것에서부터 시작할 수 있다.
그리고 필터를 구성하는 모든 요소는 분모에만 남아있다. 일반적으로 분자에 있는 s 요소들을 zero라고 하고, 분모에 있는 s 요소들을 pole이라고 한다. Butterworth filter는 pole만 남아있고, zero는 어디갔는지 알 수 없기 때문에 이러한 형태의 필터를 All-pole filter라고 한다. 그렇다면, 왜 all-pole필터가 고안되었는지, 그 이유에 대해서 생각해보자. 그리고 왜 all-zero 필터 보다 all-pole필터가 최종적으로 남게 되었는가?
이 질문에 대한 답은 모든 종류의 필터(Low pass filter, High pass filter, band pass filter, notch filter)는 모두 Lowpass filter에서 유도될 수 있기 때문이다. 즉, 기초적인 Lowpass Filter를 (나중에 Normalized Low pass filter에 대해서 공부하게 된다.) 수학적으로 구성해낼 수 있다면, 나머지 필터를 구성할 수 있다. 그렇다면, Lowpass Filter와 All-Pole 필터의 관계는? Pole은 통과대역을 지정시켜주기 때문이다.
즉, pole이 생긴 지점을 통해서 입력함수는 출력함수로 filter되면서 살아남는다. zero가 생긴 지점을 통해서는 입력함수가 출력함수로 filter 되면서 없어진다. 그럼, all-pole 필터에는 zero가 없는데 zero는 왜 논의하는 것인가? 그것은 pole만 존재하거나 zero만 존재하는 필터는 존재하지 않기 때문이다.
all-pole 필터에도 zero가 존재한다. 단지 zero인 s는 모두 $\infty$로 가버리기 때문에 보이지 않는다. 그래서 또 한번 $\Omega\rightarrow\infty$인 주파수를 가지는 input signal은 모두 없어지게 된다. 즉, All-pole filter는 Lowpass filter를 짜기 위한 조건을 쉽게 제안해줄 수 있는 요소들을 가지고 있다. 우리가 볼 두 종류의 필터(Butterworth, Chebyshev)는 모두 All-pole filter이다.
3. Filter specification
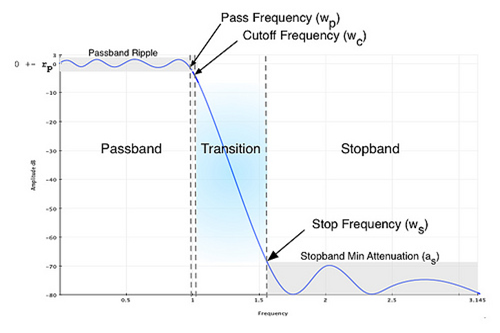
출처 : SPrelated.com / Pytho scipy.signal IIR filter Design
우리는 지금까지 필터는 일종의 시스템이라는 것을 배웠고, 두 종류의 가장 많이 쓰이는 필터가 있다는 것을 배웠다. 또한 이 시스템의 계수를 적절히 조절함으로써 이 시스템을 필터로 만들어 사용할 수 있다는 것 또한 배웠다. 그렇다면, 그 계수를 어떻게 적절히 조절할 것인가? 혹은 그 계수를 무엇을 위해서 조절할 것인가에 대해서 생각해보지 않을 수 없다.
일반적으로 filter는 원하는 주파수 영역대를 살리고, 나오지 않아야하는 주파수 영역대는 죽여줘야 하는 사명을 갖고 태어나게 해야한다. 그것은 filter specification이라는 것을 통해서 요구할 수 있다. 가장 완벽한 필터는 transition의 기울기가 수직인, 통과시키고 싶은 부분의 주파수 요소만 통과시키는 필터이다. 하지만 이런 필터는 존재하지 않는다. 그 이유는 몇 가지로 생각해볼 수 있다.
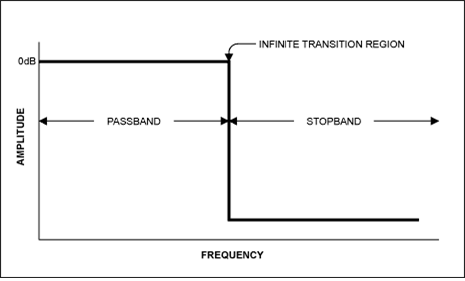
ideal filter는 위와 같이 생겼다. frequency 영역에서는 큰 문제가 없는 것처럼 단순하게 생겼지만 이것을 시간 영역으로 다시 역 푸리에 변환하게 되면, 실제로 이런 필터가 존재할 수 없다는 사실을 알게 된다. ideal filter를 역 푸리에 변환 하게 된 필터는 sinc function이기 때문이다. 일반적인 sinc function은 causal하지 않고, impuse response의 길이가 무한하기 때문이다.
어쨌든, 현실적인 필터 시스템을 만들기 위해서는 적절히 타협된 필터를 구성해내는 것이 더 중요하다고 할 수 있다. 그래서 데시벨을 이용해서 –2dB지점에서 passband frequency를 갖고, -40dB지점에서 stopband frequency를 가지는 filter를 구성해주세요! 라고 타협적으로 엔지니어에게 요구하게 되는 것이다. 이 요구 조건을 가지고 우리는 Butterworth filter의 차수를 어떻게 조절해야 하는지, cutoff frequency($\Omega_c$)는 어떻게 맞춰야 하는지 등등에 대해서 공부해보자.
4. Butterworth filter의 모습과 How to satisfy specifications
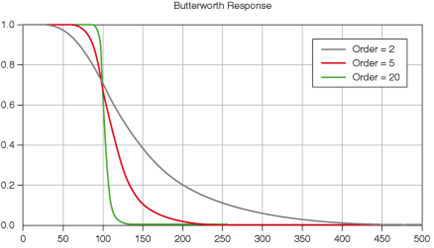
일반적으로 버터워스 필터의 형태는 위와 같다. 우리는 단지 그냥 “워후! 이런 것이 있구만!” 하고 가져다 쓰면 되겠지만, 그에 앞서서 어떻게 해서 저런 모양이 생기게 되는지 수학적으로 확인해볼 필요가 있다. 다시 한번 버터워스 필터의 식을 가져다 생각해보자.
\[|H_a(j\Omega)|^2 = 1 / \left\lbrace 1+\left(\frac{\Omega}{\Omega_c}\right)^{2N}\right\rbrace\]우리가 먼저 해볼 수 있는 것은 이 버터워스 필터의 식을 $\Omega=0$일 때 미분해보고, $\Omega=\infty$일 때 미분해보면서 그 기울기가 양 끝에서 어떻게 되는지 알아보는 것이다.
먼저, 식을 조금 단순화시켜보자.
\[|H_a(j\Omega)|=\left[1+\left(\frac{\Omega}{\Omega_c}\right)^{2N}\right]^{1/2}\]그러면 여기서 $\Omega$에 대하여 양 변을 미분해보자.
\[\frac{d}{d\Omega}|H_a(j\Omega)| = \left[-\frac{1}{2}+\left(\frac{\Omega}{\Omega_c}\right)^{-3/2}\right] \left[2N\left(\frac{\Omega}{\Omega_c}\right)^{2N-1}\right] \left(\frac{1}{\Omega_c}\right)\] \[\therefore \left|\frac{d}{d\Omega}|H_a(j\Omega)|\right|_{\Omega = 0} = 0\]그러므로 Butterworth filter는 $\Omega=0$에서 flat 하다는 것을 알 수 있고, 이것은 이것을 계속 미분할 때에도 모두 유효하게 0이기 때문에 maximally flat하다는 것을 알 수 있다.
한편, $\Omega\rightarrow\infty$인 경우에는 어떨까.
\[|H_a(j\Omega)| = 1/\sqrt{1+\left(\frac{\Omega}{\Omega_c}\right)^{2N}}\]이므로,
$\lim_{\Omega\rightarrow \infty}|H_a(j\Omega)|$는 $\left(\frac{\Omega}{\Omega_c}\right)^{-N}$의 크기를 따르게 되므로, 0에 수렴하게 되는데 데시벨의 크기에서 한번 관찰해보면,
\[\lim_{\Omega\rightarrow \infty}|H_a(j\Omega)| = -20N \log_{10}\left(\frac{\Omega}{\Omega_c}\right)\]즉, -20N의 값에 비례하는 점근선으로써 서서히 작아지는 형태를 띈다고 생각할 수 있다. 또한, N에 대해서는, N의 크기가 클수록 분모의 크기가 빨리 커지므로, transition이 매우 가파르게 떨어지고, 더 ideal filter의 모양에 가까워진다는 것 또한 알 수 있다.
그러므로 위의 그림과 같은 Butterworth Filter의 모양과 같은 plot을 구상해 낼 수 있다.이로써, Butterworth filter의 모양을 수학적으로 생각해보았다. 하지만, 이것을 안다고 해서 filter specification을 맞출 수 있는 것은 아니다. filter의 specification에 대해서 이제 더 생각해보자.
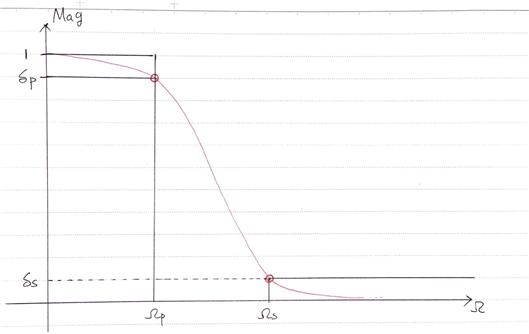
일반적인 Butterworth Filter에 대해서, 어떤 차수의 Butterworth filter 이든지 상관없이 모두 $(\Omega_p,\delta_p)$와 $(\Omega_s,\delta_s)$을 지난다는 것을 알고 있다. 그러므로 두 식을 구할 수 있게 된다. 버터워스 필터의 일반식 식 (10) 으로부터
① $\Omega=\Omega_p$ 일 때,
\[1/\left\lbrace1+\left(\frac{\Omega_p}{\Omega_c}\right)^{2N}\right\rbrace=\delta^2_p\]② $\Omega=\Omega_s$ 일 때,
\[1/\left\lbrace1+\left(\frac{\Omega_s}{\Omega_c}\right)^{2N}\right\rbrace=\delta^2_s\]두 식으로부터 역수를 취하고, 항을 옮겨주면,
식 (16)으로 부터,
\[\left(\frac{\Omega_p}{\Omega_c}\right)^{2N} = \delta_p^{-2}-1\]식 (17)로 부터,
\[\left(\frac{\Omega_s}{\Omega_c}\right)^{2N} = \delta_s^{-2}-1\]를 얻을 수 있게 된다.
이 때, 식 (18)/식 (19)은 다음과 같이 표현될 수 있다. (ratio of the two equations)
\[\left(\frac{\Omega_p}{\Omega_s}\right)^{2N} = \frac{\delta^{-2}_p-1}{\delta_s^{-2}-1}\]식 (20)의 양변에 밑이 10인 로그를 취해주면,
\[2N = \log_{10}\left(\frac{\delta^{-2}_p-1}{\delta_s^{-2}-1}\right) / \log_{10}\left(\frac{\Omega_p}{\Omega_s}\right)\] \[N = \frac{1}{2}\log_{10}\left(\frac{\delta^{-2}_p-1}{\delta_s^{-2}-1}\right) / \log_{10}\left(\frac{\Omega_p}{\Omega_s}\right)\] \[N = \log_{10}\sqrt{\frac{\delta^{-2}_p-1}{\delta_s^{-2}-1}} / \log_{10}\left(\frac{\Omega_p}{\Omega_s}\right)\]이렇게 $N$을 구할 수 있다. 하지만 N은 정수이기 때문에 실제적으로 사용할 수 있는 N을 만족하는 식은
\[N \geq \log_{10}\sqrt{\frac{\delta^{-2}_p-1}{\delta_s^{-2}-1}} / \log_{10}\left(\frac{\Omega_p}{\Omega_s}\right)\]이며, 이 때 위 식을 만족하는 최소의 N을 찾으면 된다.
또, $\Omega_c$(cutoff frequency)를 알 수 있다면 원하는 specification을 만족하는 design의 Butterworth filter를 설계할 수 있을 것이다.
$\Omega_c$를 구할 때에는, Filter의 함수는 무조건 $(\Omega_p,\delta_p)$를 지나야 한다는 조건을 가지고 구할 수 있다.
여기서 $(\Omega_s,\delta_s)$를 지나지는 않느냐는 생각을 가질 수도 있겠다. 하지만, 실제로는 $N$의 조건은 식 (24)를 만족하는 정수이기 때문에 $(\Omega_s,\delta_s)$을 지날 수 없게 필터가 설계되게 된다.
그러므로 $\Omega_c$를 구할 때에는 $(\Omega_p,\delta_p)$을 지난다는 조건을 가지고 찾는 것이 현실적이고, 바람직한 방법이다. 그러므로, $\Omega_c$는,
\[1/\left\lbrace 1+\left(\frac{\Omega_p}{\Omega_c}\right)^{2N}\right\rbrace = \delta_p^2\]의 식으로부터
\[\left(\frac{\Omega_p}{\Omega_c}\right)^{2N} = \delta_p^{-2}-1\]를 만족하는 $\Omega_c$를 찾으면 된다.
그렇다면, 우리는 지금까지 Butterworth filter의 $\Omega=0$과 $\Omega=\infty$일 때의 모양에 대해서 간략하게 알아보고, specification을 따르는 N과 $\Omega_c$를 구하는 방법에 대해서 알아보았다.
그러면 우리는 N과 $\Omega_c$를 알기 때문에 아날로그 필터 시스템으로 설계할 수 있을까? 그것에 대한 정답은 ‘아직은 불가능하다’이다.
왜냐하면, 일반적으로 아날로그 시스템을 설계할 때에는 시스템의 식을 Laplace frequency, $s$에 대해서 알아야하기 때문이다.
일반적으로 Laplace frequency를 이용해서 정의된 시스템의 식을 Transfer function이라고 부른다.
5. Butterworth filter의 transfer function (s-domain)
먼저 우리는 식 (10)으로부터 Butterworth filter를 s-domain에 mapping 시켜보고, 그것 중 stable한 값을 가지는 $s$만을 취해서 일반적인 아날로그 필터인 $|H_a(s)|$를 도출하도록 하겠다. 그리고 그 $|H_a(s)|$의 일반식을 유도하는 과정을 알아보도록 하자.
먼저, $s=j\Omega$라는 transformation을 통해서 를 s-domain에 쉽게 표현할 수 있다. 즉, 다음의 식이 성립한다.
\[|H_a(j\Omega)|^2 = H_a(s)H_a(-s)\]여기서 s 부분과 –s부분으로 굳이 나눈 이유는, 나중에 알게 되겠지만 s는 $\pm$의 복호로 나눠지게 되는데 이 때, 양의 값을 가지는 s만 stable하기 때문이다. 그러므로
\[H_a(s) H_a(-s) = 1/\left\lbrace 1+\left(\frac{-s^2}{\Omega_c^2}\right)^N\right\rbrace\]으로 일반화 할 수 있다.
여기서 $s$로 표현되는 pole의 값들을 구하고 그 pole들로 $s$-domain의 일반화된 $|H_a(s)|$를 나타낼 수 있다면, 어떤 N에 대해서도 s-domain에서 표현되는 Butterworth filter의 Transfer function을 얻을 수 있다.
Pole은 분모의 값이 0이 되도록 하는 s의 값으로 정의되기 때문에, pole의 정의에 따르면,
\[1+\left(\frac{-s^2}{\Omega_c^2}\right)^N = 0\]이 되는 s는 Butterworth Filter의 pole이라고 할 수 있다.
\[\Rightarrow \left(\frac{-s^2}{\Omega_c^2}\right)^N = (-1) = \exp\left(j(2k-1)\pi\right)\text{ for } k = 1, 2, \cdots, N\] \[\Rightarrow \left(\frac{-s^2}{\Omega_c^2}\right)=\exp\left(j\frac{2k-1}{N}\pi\right)\] \[s_k^2 = -\Omega_c^2\exp\left(j\frac{2k-1}{N}\pi\right)\text{ for }k= 1, 2, \cdots, N\] \[\therefore s_k = \pm j\Omega_c^2\exp\left(j\frac{2k-1}{2N}\pi\right)\text{ for }k= 1, 2, \cdots, N\]즉, 여기서 $s_k$는 양의 값과 음의 값 두 가지로 나뉘게 된다. 하지만, $s_k$는 양의 값을 가질 때 그 값들이 모두 s-plane의 Left Hand Plane에 존재하게 되어서 양의 $s_k$만 stable한 시스템을 구성할 수 있다. 1
그러므로, 양의 $s_k$가 항상 Left Hand Plane에 존재한다는 것을 증명하겠다. 여기서 양의 $s_k$가 항상 Left Hand Plane에 존재하기 때문에 음의 $s_k$는 항상 Right Hand Plane에 존재한다는 것을 알 수 있으므로, 증명은 생략하도록 하겠다.
PROOF 1 : The location of positive $s_k$ in $s$-domain
양의 $s_k$에 대해서
\[s_k^+= j\Omega_c\exp\left(j\frac{2k-1}{2N}\pi\right)\text{ for }k = 1, 2, \cdots, N\] \[=j\Omega_c\left(\cos\left(\frac{2k-1}{2N}\pi\right)+j\sin\left(\frac{2k-1}{2N}\pi\right)\right)\] \[=\Omega_c\left(j\cos\left(\frac{2k-1}{2N}\pi\right)-\sin\left(\frac{2k-1}{2N}\pi\right)\right)\]여기서
\[\sin\left(\frac{2k-1}{2N}\pi\right) = \left\lbrace \sin\left(\frac{1}{2N}\pi\right), \text{ } \sin\left(\frac{3}{2N}\pi\right), \text{ } \sin\left(\frac{5}{2N}\pi\right), \cdots, \text{ } \sin\left(\frac{2N-1}{2N}\pi\right) \right\rbrace\]라는 사실을 쉽게 알 수 있다.
그런데 모든 $\sin\left(\frac{2k-1}{2N}\pi\right)$는 1,2 사분면위에 위치하게 되고, 이 값들은 모두 양수이다. 그렇기 때문에 $s_k$의 실수부는 항상 음수의 값을 가지게 된다.
따라서 $s_k^+=j\Omega_c\exp\left(j\frac{2k-1}{2N}\pi\right)$는 $N$의 값에 관계없이 항상 $s$-plane의 Left Hand Pole이다.
Q.E.D.
그렇기 때문에 일반적으로,
\[s_k = \Omega_c\left(-\sin\left(\frac{2k-1}{2N}\pi\right)+j\cos\left(\frac{2k-1}{2N}\pi\right)\right)\text{ for }k = 1, 2, \cdots, N\]이라는 pole 값을 이용한다면, stable Butterworth system을 만들 수 있게 된다.
그렇기 때문에, 일반적으로 stable한 Butterworth Filter System은 $s$-domain에서 다음과 같이 정의될 수 있다.
\[H_a(s) = 1/\left\lbrace1+\left(\frac{s}{\Omega_c}\right)^N\right\rbrace\] \[=\Omega_c / \left\lbrace\prod_{k=1}^{N}\left(\frac{s}{\Omega_c} - \hat{s}_k\right)\right\rbrace\notag\] \[\text{ where } \hat{s}_k = \Omega_c\left(-\sin\left(\frac{2k-1}{2N}\pi\right) + j\cos\left(\frac{2k-1}{2N}\right)\pi\right)\]또는,
\[H_a(s) = 1/\prod_{k=1}^{N}\left(\frac{s}{\Omega_c}-s_k\right)\notag\] \[\text{ where } s_k = -\sin\left(\frac{2k-1}{2N}\pi\right) + j\cos\left(\frac{2k-1}{2N}\pi\right)\]로 정의할 수 있다.
그러므로, 각 $N$에 대하여 풀어서 생각해본다면 다음과 같다고도 할 수 있다.
$N$=1 인 경우,
\[H_a(s) = 1/\left(\frac{s}{\Omega_c}-s_1\right)\notag\] \[\text{ where }s_1 = -\sin\left(\frac{1}{2}\pi\right)+j\cos\left(\frac{1}{2}\pi\right)=-1+0j = -1\] \[\therefore H_a(s) = 1/\left(\frac{s}{\Omega_c}+1\right)=\frac{\Omega_c}{s+\Omega_c}\]$N$=2 인 경우,
\[H_a(s) = 1/\left\lbrace\prod_{k=1}^{2}\left(\frac{s}{\Omega_c}-s_k\right)\right\rbrace = 1/\left\lbrace\left(\frac{s}{\Omega_c}-s_1\right) \left(\frac{s}{\Omega_c}-s_2\right)\right\rbrace\]where
\[s_1 = -\sin\left(\frac{1}{4}\pi\right)+j\cos\left(\frac{1}{4}\pi\right)\] \[=-\frac{\sqrt{2}}{2}+j\frac{\sqrt{2}}{2}\] \[s_2 = -\sin\left(\frac{3}{4}\pi\right)+j\cos\left(\frac{3}{4}\pi\right)\] \[=-\frac{\sqrt{2}}{2}-j\frac{\sqrt{2}}{2}\]따라서,
\[\therefore H_a(s) = \left\lbrace1/\left(\frac{s}{\Omega_c}+\frac{\sqrt{2}}{2}-j\frac{\sqrt{2}}{2}\right)\right\rbrace \left\lbrace1/\left(\frac{s}{\Omega_c}+\frac{\sqrt{2}}{2}+j\frac{\sqrt{2}}{2}\right)\right\rbrace\] \[=\Omega_c^2 / \left(s^2 + \sqrt{2}s\Omega_c + \Omega_c^2\right)\]$N$=3인 경우,
이 쯤 오면 굉장히 지친다. 살짝 꼼수를 써보자. 먼저, $\Omega_c=1$이라고 한 다음, $s = \frac{s}{\Omega_c}$로 치환하면 같은 결과를 얻게 된다. 이 방법은 나중에 배우게 되는 Denormalization 방법이다.
\[H_a(s)|_{\Omega_c = 1} = 1/\prod_{k=1}^{N}(s-s_k)\] \[=\frac{1}{(s-s_1)(s-s_2)(s-s_3)}\]이고, 여기서
\[s_1 = -\sin\left(\frac{1}{6}\pi\right)+j\cos\left(\frac{1}{6}\pi\right) = -\frac{1}{2}+j\frac{\sqrt{3}}{2}\] \[s_2 = -\sin\left(\frac{3}{6}\pi\right) + j \cos\left(\frac{3}{6}\pi\right) = -1\] \[s_3 = -\sin\left(\frac{5}{6}\pi\right)+j\cos\left(\frac{5}{6}\pi\right)=-\frac{1}{2}-j\frac{\sqrt{3}}{2}\]이다.
따라서, $s_1$, $s_2$, $s-3$을 대입하면,
\[H_a(s) = 1/\left[(s+1)\left\lbrace(s+\frac{1}{2})^2 + \frac{3}{4}\right\rbrace\right]\] \[=\frac{1}{(s+1)(s^2 + s + 1)}\] \[=\frac{1}{s^3 + 2s^2 + 2s + 1}\]여기서 $s = s/\Omega_c$로 치환한다면,
\[H_a(s) = \frac{\Omega_c^3}{s^3 + 2\Omega_cs^2 + 2\Omega_c^2s + \Omega_c^3}\]임을 알 수 있다.
여기까지 보면, 일반적으로 $N$이 홀수인 경우와 짝수인 경우의 pole값이 차이가 있다는 것을 알 수 있다. 만약 $N$이 홀수라면 $s$가 real number인 pole이 하나 있고 나머지는 모두 complex number이고, $N$이 짝수라면 모두 complex number의 pole을 갖는다는 것을 알 수 있다. 그 이유는 다음과 같다.
\[s_k = -\sin\left(\frac{2k-1}{2N}\pi\right)+j\cos\left(\frac{2k-1}{2N}\pi\right)\]에서
\[\frac{2k-1}{2N}\pi = \frac{1}{2}\pi\]가 되는 지점이 반드시 생기기 때문인데, 그 $k$는 $k=(N+1)/2$인 점이다.
즉, $N$이 홀수 일 때 $k=(N+1)/2$ 인 점에서는 $s_k$가 반드시 $–1$이 된다.
더불어, 일반적으로
\[\cos\left(\pi-\theta\right)=-\cos(\theta)\] \[\sin\left(\pi-\theta\right)=\sin(\theta)\]이기 때문에, 모든 $s_p$는 $s_{N-p+1}$와 complex conjugate를 이루게 된다.
그렇기 때문에, $S_{N-p+1} = s^*_p$라고 할 수 있다.
더불어,
\[s_p+s^*_p = 2\sin\left(\frac{2k-1}{2N}\pi\right)\]이고,
\[s_ps^*_p=1\]인 성질을 갖는다.
그렇기 때문에,
\[(s-s_p)(s-s^*_p)=s^2-s(s_p+s^*_p)+s_ps^*_p=s^2 +2s\sin\left(\frac{2p-1}{2N}\pi\right)+1\]이므로, $H_a(s)$는 다음과 같이 생각할 수 있다.
$N$이 짝수일 때,
\[H_a(s) = \Omega_c^N / \left\lbrace\prod_{k=1}^{N/2}\left(s^2 + b_k\Omega_c s + \Omega_c^2\right)\right\rbrace\notag\] \[\text{ where }b_k = 2\sin\left(\frac{2k-1}{2N}\pi\right)\]N이 홀수일 때,
\[H_a(s) = \Omega_c^N / \left\lbrace(s+\Omega_c) \prod_{k=1}^{\frac{N-1}{2}}\left(s^2 + b_k\Omega_c s + \Omega_c^2\right)\right\rbrace\notag\] \[\text{ where }b_k = 2\sin\left(\frac{2k-1}{2N}\pi\right)\]이로써, 우리는 Butterworth Filter의 s-domain에서의 일반적인 transfer function을 구했다.
종합하자면,
\[N \geq \log_{10}\sqrt{\frac{\delta^{-2}_p-1}{\delta_s^{-2}-1}} / \log_{10}\left(\frac{\Omega_p}{\Omega_s}\right)\]이라는 식을 통해서 N을 구할 수 있고,
\[\left(\frac{\Omega_p}{\Omega_c}\right)^{2N} = \delta_p^{-2}-1\]라는 식을 통해서 $\Omega_c$를 구할 수 있다.
거기에, N이 짝수일 때,
\[H_a(s) = \Omega_c^N / \left\lbrace\prod_{k=1}^{N/2}\left(s^2 + b_k\Omega_c s + \Omega_c^2\right)\right\rbrace\notag\] \[\text{ where }b_k = 2\sin\left(\frac{2k-1}{2N}\pi\right)\]N이 홀수일 때,
\[H_a(s) = \Omega_c^N / \left\lbrace(s+\Omega_c) \prod_{k=1}^{\frac{N-1}{2}}\left(s^2 + b_k\Omega_c s + \Omega_c^2\right)\right\rbrace\notag\] \[\text{ where }b_k = 2\sin\left(\frac{2k-1}{2N}\pi\right)\]을 통해서 일반적인 $s$-domain에 대해 Butterworth filter를 정의할 수 있게 된다.