클러스터링 문제

머신러닝은 크게 지도학습 문제와 비지도학습 문제로 나눌 수 있다. 비지도학습에서 가장 자주 등장하는 응용 중 하나는 클러스터링이다.

클러스터링은 주어진 학습 데이터 $\lbrace x^{(1)},\cdots,x^{(m)}\rbrace$에 대하여 위치가 가까운 데이터들을 각자의 그룹으로 라벨을 지어주는 과정을 의미한다.

만약 아래의 그림 1과 같이 데이터들이 주어져있다고 해보자. 이 때, 각 데이터들은 라벨이 주어져 있지는 않은 상태라고 생각해보자.

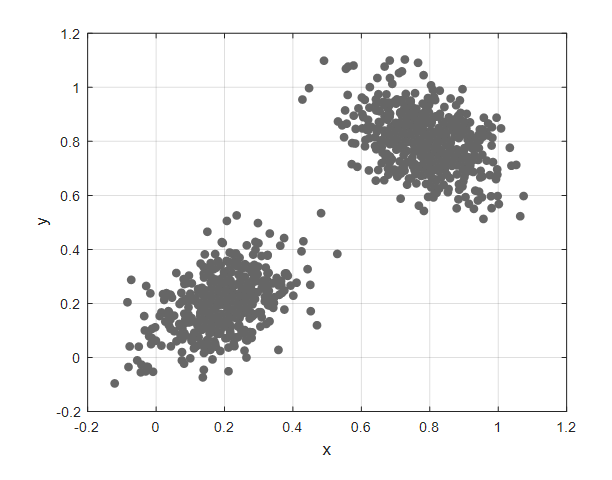
그림 1. 라벨이 주어져 있지 않은 데이터셋. 이 데이터셋을 두 개의 클러스터로 나누면 어떻게 그룹핑 하는 것이 좋을까?

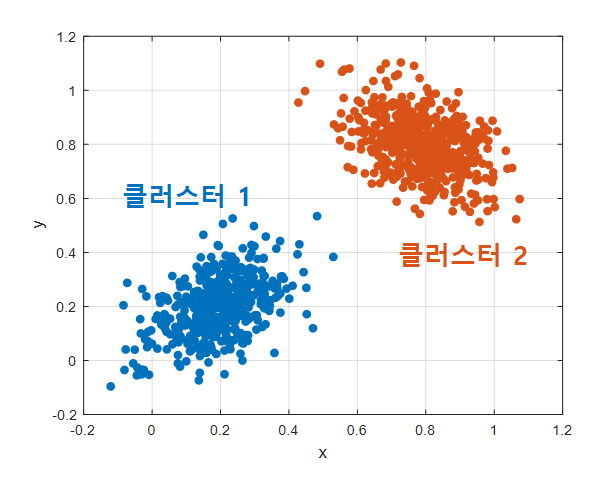
그림 2.

그림 3. k-means 알고리즘의 수행 과정

k-means 알고리즘

Initialize cluster centroids $\mu_1, \mu_2, \cdots, \mu_k \in \Bbb{R}^n$ randomly

Repeat Until Convergence: {

$\quad$ For every $i$, set

\[c^{(i)}=\underset{j}{\text{arg min}} ||x^{(i)}-\mu_j||^2\]

$\quad$ For every $j$, set

\[\mu_j := \frac{\sum_{i=1}^{m}1\lbrace c^{(i)}=j\rbrace x^{(i)}}{\sum_{i=1}^{m}1\lbrace c^{(i)}=j\rbrace}\]

}

여기서 $k$는 클러스터의 개수이다 (그래서 k-means 알고리즘이다). 클러스터의 개수를 선택할 수 있게 도와주는 여러 방법이 있지만 결국은 데이터를 직접 눈으로 보고 $k$ 값을 결정하는 과정을 피할 수는 없다.

또, $1\lbrace \text{condition} \rbrace$ 함수는 condition이 True인 경우 1 아닌 경우 0을 출력해주는 함수이다. 즉, $1\lbrace c^{(i)}=j\rbrace$ 함수는 $i$ 번째 데이터의 클래스가 $j$인 경우 1 아니면 0을 출력해주는 것과 같다.