※ 본 포스팅의 내용은 Thomas Judson의 The ordinary differential equations project에서 많은 부분을 차용하였음을 밝힙니다.
변수분리형 1계 미분방정식
가장 간단한 형태의 미분방정식 중 하나는 다음과 같은 변수분리형 1계 미분방정식이다.
\[\frac{dy}{dx}=M(x)N(y)\]식 (1)을 보면 $x$에 대한 식 $M(x)$와 $y$에 대한 식 $N(y)$가 깔끔하게 분리되어 있는 것을 볼 수 있다.
간단한 예시
식 (1)은 조금 복잡할 수도 있는데, $M(x)$와 $N(y)$를 조금 바꿔서 구체적인 예시를 들어보면 다음과 같은 것이 변수분리형 1계 미분방정식이다.
\[\frac{dy}{dx}=y % 식 (2)\]식 (2)는 자세히 보면, 어떤 함수 $y$를 $x$에 대해 미분을 했을 때 여전히 $y$가 나올 수 있게 되는 함수를 묻는 방정식이다.
잘 생각해보면 이런 방정식의 solution은
\[y=Ce^x% 식 (3)\]임을 알 수 있다. (여기서 $C$는 적분상수이다.)
어떻게 이런 결과를 얻을 수 있을까?
방법은 $x$에 관한 식과 $y$에 관한 식들을 좌변과 우변에 각각 몰아넣고, 적분함으로써 가능하다.
좀 더 구체적으로 식 (2)를 풀어보면 다음과 같이 풀 수 있다.
식 (2)의 양변을 $y$로 나눠주면,
\[식(2)\Rightarrow \frac{1}{y}\frac{dy}{dx}=1\]이고, 여기서 양변을 $dx$로 곱하면 좌변에는 $y$에 관한 식, 우변에는 $x$에 관한 식으로 몰아넣은 것과 같다.
\[\Rightarrow \frac{1}{y}dy=dx\]따라서,
여기서 양변을 적분하면 다음과 같다.
\[\Rightarrow\int\frac{1}{y}dy=\int 1 dx\]따라서,
\[\Rightarrow \ln |y| = x + C\]여기서 $C$는 적분상수이다.
식을 조금만 수정하면
\[y = \exp(x+C)\] \[y = C\exp(x)\]와 같은 결과를 얻을 수 있음을 알 수 있다.
변수분리형 1계 미분방정식의 solution
조금 더 이론적으로 변수분리형 1계 미분방정식의 solution을 어떻게 계산하게 된 것인지 알아보자.
일반적으로 식 (1)과 같은 변수분리형 1계 미분방정식의 solution은 아래와 같이 계산할 수 있다.
\[식(1) \Rightarrow M(x)dx = \frac{1}{N(y)}dy\]식을 약간 수정해 $M(x)$를 $f(x)$라 두고 $1/N(y)$를 $-g(y)$라 두면,
\[f(x)dx+g(y)dy=0\]과 같이 쓸 수 있다. 여기서 양변에 적분 상수를 취해주면,
\[\int f(x)dx + \int g(y) dy=C\]이고, $f(x)$의 부정적분이 $F(x)$라고 하고, $g(y)$의 부정적분이 $G(y)$라고 하면,
\[\Rightarrow F(x) + G(y) = C\]라고 할 수 있다.
여기서 $C$는 적분 상수이다.
여기서 초기값이 $y(x_0)=y_0$로 주어진다면 적분상수 $C$는 다음과 같이 계산할 수 있게 된다.
\[F(x_0)+G(y_0) = C\]변수분리법을 이용해 풀 수 있는 미분방정식 모델
변수분리법은 간단하지만 의외로 이 방법을 이용해 풀 수 있는 미분방정식 모델들이 있다.
뉴턴의 냉각법칙
뉴턴의 냉각법칙은 주변 온도보다는 뜨거운 물체가 있을 때, 그 물체의 온도가 식는 속도가 주변의 온도와의 온도차에 비례한다는 법칙이다.
생각해보면 자연스러운 것이, 뜨거운 물체는 주변 온도와의 온도 차가 클 수록 더 빨리 식는다. (뜨거운 냄비에 미지근한 물을 끼얹는 것보다 차가운 물을 끼얹는게 더 빨리 냄비를 식히는 방법이다.)
수식으로 정리하면, 내가 관심을 갖고 있는 물체의 온도가 $T$라고 하고 주변 온도가 $T_m$이라고 하면 다음과 같은 관계를 갖는다는 말이다.
\[\frac{dT}{dt}=k(T-T_m)\]여기서 $k$는 음수이다. 그래야 시간에 따라 관심 물체의 온도 $T$가 서서히 떨어지게 된다.
가령 주변 온도가 20도 이고 관심 물체의 온도가 처음에 100도 였고 1초 뒤에 98도 였다고 하면,
\[\frac{dT}{dt}=k(T-20)\]이고, $T$에 관한 식을 모두 좌변에, $t$에 관한 식을 모두 우변에 넘겨주면,
\[\frac{1}{(T-20)}dT = kdt\]이다.
양변을 적분해주면,
\[\ln(T-20)=kt+C\] \[\Rightarrow T-20 = Ce^{kt}\] \[\therefore T = 20 + Ce^{kt}\]이다.
여기서 $T(0)=100$이었고 $T(1)=98$이라고 하므로,
\[T(0) = 20+C = 100\] \[T(1) = 20 + Ce^k=98\] \[\therefore C = 80, k = -0.0253\]임을 알 수 있다.
따라서, 이 물체의 온도 변화를 그래프로 그려보면 다음과 같다.
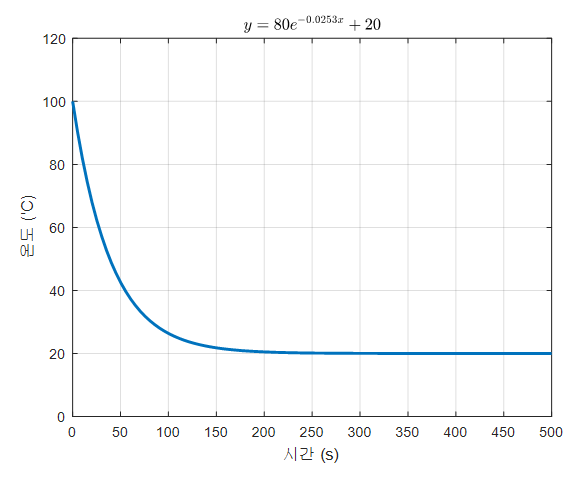
그림 1. 뉴턴의 냉각법칙을 적용한 물체의 냉각 현상 curve
시간에 따른 소금 농도 변화
초등학교 수학 시간에는 소금물 농도 문제가 그렇게나 어려웠다.
초등학교 때 소금물 문제를 풀 때는 소금물을 합치고 잘 섞어서 섞여진 소금물의 농도를 맞추는 것이 문제였다.
그런데, 소금물 두 컵을 잘 섞어서 농도를 확인하는게 아니고, 맹물이 들어있던 물탱크에 특정 농도의 소금물을 꾸준히 붓는다면 시간에 따른 소금물의 농도를 확인할 수도 있지 않을까?
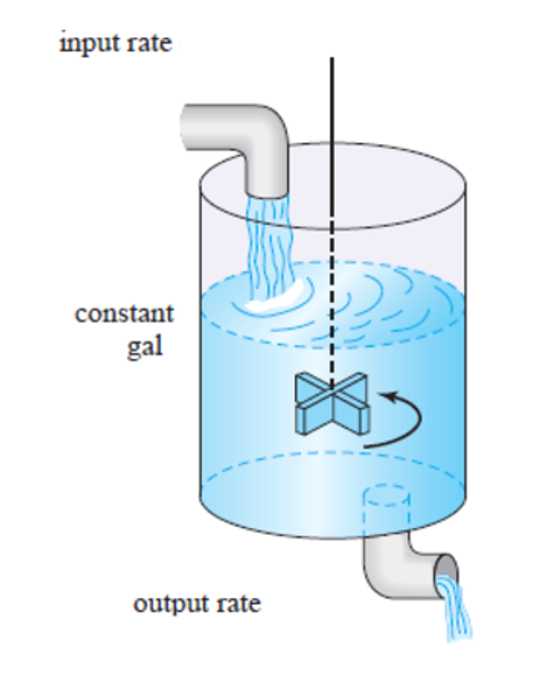
그림 2. 물탱크에 소금물을 서서히 섞어주는 타입의 문제가 상정하는 상황
그림 출처: Solution to the ODE-mixing tank problem using artificial neural networks, , Aaron U Aquino & Elmer Dadios, 2015
물만 들어있는 1000리터 짜리 물탱크에 0.5kg/L 농도의 소금물을 계속해서 넣어준다고 생각해보자.
우리의 목표는 물탱크에 0.5kg/L 농도의 물로 가득채우는 것인데, 이 때, 물탱크의 수위는 원래대로 유지해주고 싶다고 해보자.
이를 위해서 0.5kg/L 농도의 소금물을 1분에 10L 씩 넣어주고 물탱크에 들어있던 물도 1분에 10L씩 빼준다고 해보자.
여기서 우리는 물탱크에 소금이 균일하게 섞일 수 있도록 계속해서 물탱크의 물을 저어준다고 가정할 것이다.
이 문제는 미분방정식을 이용해 풀 수 있는데, 물탱크 안의 소금 양을 $x(t)$라고 해보자.
그러면, 물탱크 안의 소금의 시간에 따른 변화율은 $dx/dt$ 일 것이다.
또, 소금의 시간 당 변화율은 들어오는 소금의 비율과 나가는 소금의 비율의 차이이므로,
\[\frac{dx}{dt}=\text{rate in }-\text{ rate out}\]이라고 쓸 수 있다.
들어오는 소금은 1분에 10L가 들어오는데 소금의 양은 0.5kg/L였으므로 1분 당 총 5kg의 소금이 들어온다.
나가는 물의 양은 매 분마다 10L인데, 수위는 그대로 유지해주고 있어 1000L를 유지하므로 현재 소금양의 $1/100$만큼 나가는 것으로 볼 수 있다. 따라서,
\[\frac{dx}{dt}=5-\frac{x}{100}\]과 같이 식을 세워줄 수 있는 것이다. 물론 처음에는 물에 소금이 들어있지 않았으므로 $x(0)=0$이다.
이 식은 변수분리법으로 풀어줄 수 있다.
\[\frac{dx}{500-x}=\frac{dt}{100}\]양변을 적분해주면,
\[\Rightarrow -\ln|500-x| = \frac{t}{100}+C\]즉,
\[500-x = Ce^{-0.01t}\]여기서 초기조건을 이용하면,
\[\Rightarrow x(t) = 500-500 e^{-0.01t}\]이다.
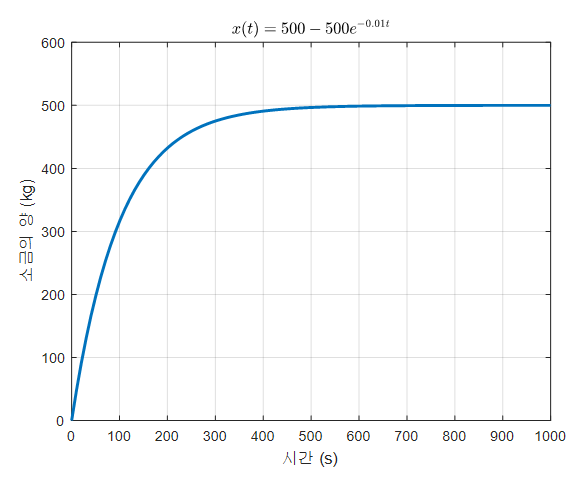
그림 3. mixing problem의 solution curve