베이즈 정리의 공식

우선 베이즈 정리의 공식부터 확인해보도록 하자. 베이즈 정리의 공식은 아래 식 (1)과 같다.

\[P(H|E) = \frac{P(E|H)P(H)}{P(E)}\]

식 (1)에는 총 네 개의 확률값이 적혀져 있으며, 생김새도 거의 비슷비슷해 그냥 보기에는 의미를 파악하기가 어렵다.

네 개의 확률 값 중 $P(H)$와 $P(H|E)$는 각각 사전 확률, 사후 확률이라고 부르고, 베이즈 정리는 근본적으로 사전확률과 사후확률 사이의 관계를 나타내는 정리이다.

그렇다면, 우리는 사전확률과 사후확률의 의미를 파악함으로써 베이즈 정리가 말하는 바와 그 의의를 이해할 수 있을 것이다.

베이즈 정리의 의미와 의의

결론부터 말하자면 베이즈 정리는 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해 나가는 방법(a method to update belief on the basis of new information)이다.

베이즈 정리를 이해하기 어려웠던 이유

베이즈 정리를 이해함에 있어서 가장 먼저 정리해야 할 개념은 ‘확률’에 관한 관점이다.

베이즈 정리의 의미를 이해하기 어려운 이유 중 하나는 고등학교 수준까지의 확률론에서는 ‘전통적인 관점’으로 확률을 정의해오고 이해해왔기 때문이다.

여기서는 확률이라는 단어를 ‘주장에 대한 신뢰도’로 생각해보자.

이러한 관점은 확률에 대한 베이지안 주의(Bayesianism) 관점으로 볼 수 있다. 반면, 전통적인 확률관은 빈도주의(frequentism)이라고 볼 수 있다.

가령 동전의 앞면이 나올 확률이 50%라고 하면, 빈도주의자들은 100번 동전을 던졌을 때 50번은 앞면이 나온다고 해석하고, 베이지안 주의자들은 동전의 앞면이 나왔다는 주장의 신뢰도가 50%라고 보는 것.

용어 정리

또, 식 (1)에 있는 공식에서 E와 H가 무엇인지 알아보자.

식 (1)에서 H는 Hypothesis의 약자로써 가설 혹은 ‘어떤 사건이 발생했다는 주장’을 의미한다.

거기에, 식 (1)에서 E는 Evidence의 약자로 ‘새로운 정보’를 의미한다.

따라서 $P(H)$는 어떤 사건이 발생했다는 주장에 관한 신뢰도, $P(H|E)$는 새로운 정보를 받은 후 갱신된 신뢰도를 의미한다.

그리고 $P(H)$와 $P(H|E)$는 각각 사전 확률, 사후 확률이라고 부르는데, 사전(事前), 사후(事後)라는 단어를 생각해본다면 어떤 일[事], 즉 여기선 ‘evidence를 관측하여 갱신하기 전 후의 내 주장에 관한 신뢰도’ 정도로 이해하면 될것이다.

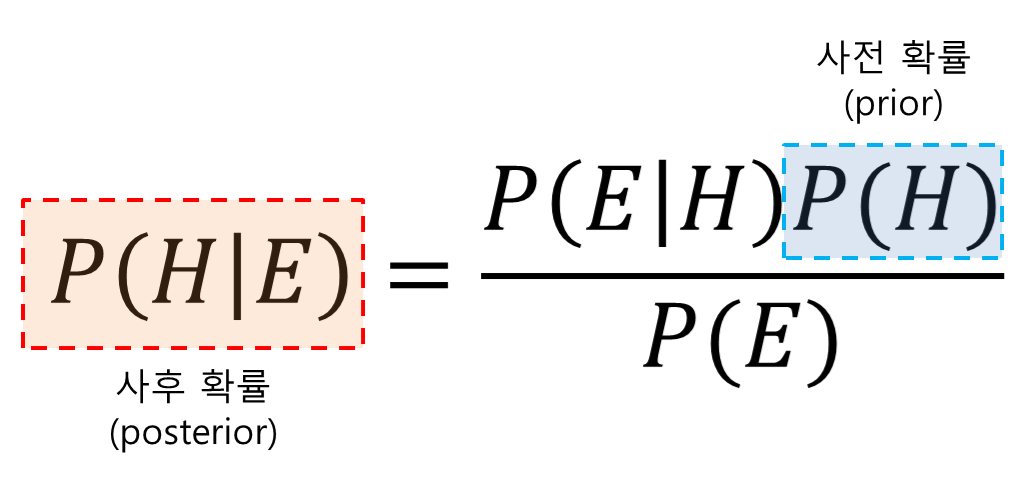
그림 1. 베이즈 정리는 사전확률과 사후확률간의 관계에 대해 설명하는 정리이다.

확률론 패러다임의 전환: 연역적 추론에서 귀납적 추론으로

베이즈 정리가 획기적인 이유는 통계학의 근본적인 패러다임을 수정했기 때문이다.

기존의 통계학은 앞서 설명했듯이 ‘빈도주의’ 관점을 기반으로 구성되어 있으며, 모두 연역적인 사고에 기반한다.

가령 전체 사건 집합에 대해 파악하고 특정 사건이 일어날 확률을 계산한다던지, 집단의 통계적인 분포를 가정하고 차이의 유의성을 검정한다던지 같은 방법들을 생각할 수 있다.

즉, 기존의 통계학에서는 엄격하게 확률 공간을 정의하거나 집단(모집단 혹은 표본집단)의 분포를 정의하고 그 뒤에 계산을 통해 파생되는 결과물들을 수용하는 패러다임을 차용한다.

반면에 베이지안 관점의 통계학에서는 사전 확률과 같은 경험에 기반한 선험적인, 혹은 불확실성을 내포하는 수치를 기반으로 하고, 거기에 추가 정보를 바탕으로 사전확률을 갱신한다.

이와 같은 방법은 귀납적 추론 방법이며, 베이지안 관점의 확률론/통계학에서는 추가적인 근거의 확보를 통해 진리로 더 다가갈 수 있다는 철학을 내포하고 있다는 점에서

확률론 패러다임에 큰 변화를 가져왔다고 할 수 있다.

문제 해결을 통한 베이즈 정리의 이해

간단한 예제 문제를 풀면서 베이즈 정리가 새로운 정보를 토대로 어떤 사건이 발생했다는 주장에 대한 신뢰도를 갱신해 나가는 방법이라는 점에 대해 좀 더 잘 이해해보도록 하자.

예제 1

질병 A의 발병률은 0.1%로 알려져있다. 이 질병이 실제로 있을 때 질병이 있다고 검진할 확률(민감도)은 99%, 질병이 없을 때 없다고 실제로 질병이 없다고 검진할 확률(특이도)는 98%라고 하자.

만약 어떤 사람이 질병에 걸렸다고 검진받았을 때, 이 사람이 정말로 질병에 걸렸을 확률은?

Solution

이런 종류의 베이즈 정리를 이용한 문제를 잘 해결하기 위해서는 앞서 언급했던 Hypothesis와 Evidence를 잘 정의할 수 있어야 한다.

이 문제에서 Hypothesis와 Evidence는 다음과 같이 정의할 수 있다.

• Hypothesis: True이다. 즉 실제로 병이 있다.
• Evidence: Positive로 출력되었다. 즉, 병이 있다고 진단 받았다.

따라서, 기본적으로 질병 A의 발병률은 0.1%이므로 임의의 사람이 이 질병에 걸렸을 확률은 $P(H)$로 쓸 수 있으며, $P(H)=0.001$이다.

또한 문제에서 주어진 민감도와 특이도는 각각 True Positive와 True Negative에 해당되는 것이고 각각 $P(E|H) = 0.99$, $P(E^c|H^c) = 0.98$이다.

이를 그림으로 나타내면 아래의 그림 2와 같다.

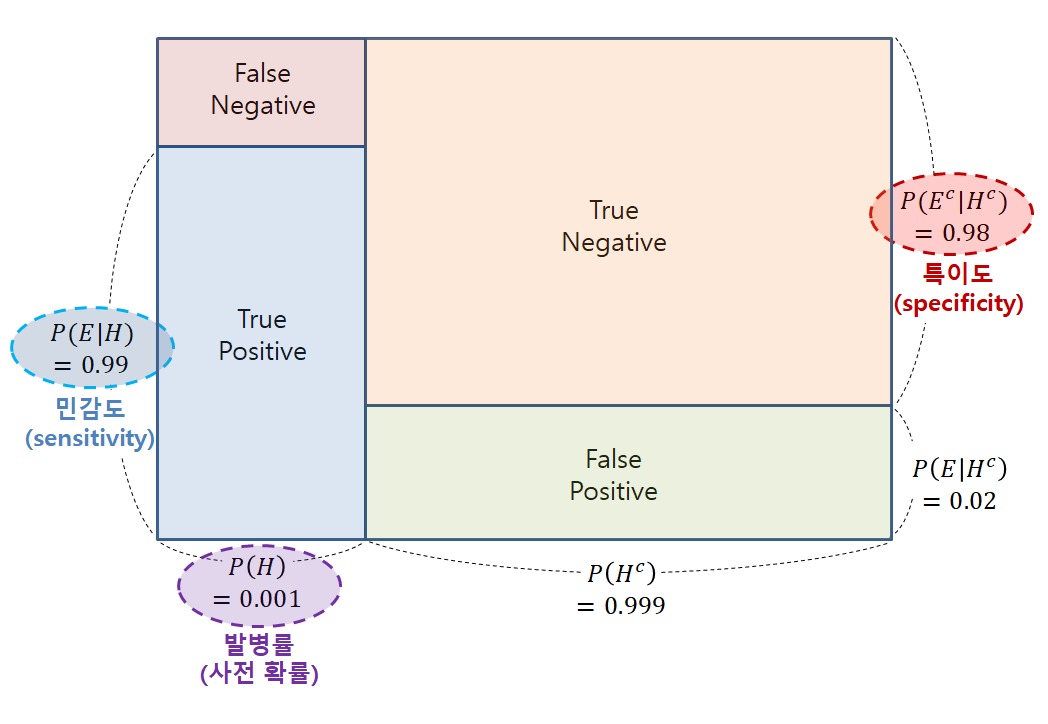
그림 2. 주어진 확률값들의 값을 사각형의 상대적 넓이로 시각화 한 것

식 (1)을 좀 더 정리해서 쓰면 아래의 식 (2)와 같다.

\[P(H|E) = \frac{P(E|H)P(H)}{P(E)} = \frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|H^c)P(H^c)}\]

따라서, 우리가 구하고자 하는 $P(H|E)$를 계산하면 결과값은 다음과 같다.

\[P(H|E) = \frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|H^c)P(H^c)} = \frac{0.001\times 0.99}{0.001\times 0.99 + 0.02\times 0.999}\notag\] \[= 0.047\text{ (소숫점 세자리까지 반올림)}\]

예제 2

예제 1에서 한 번 양성 판정을 받았던 사람이 두 번째 검진을 받고 또 양성 판정을 받았을 때, 이 사람이 실제로 질병에 걸린 확률은?

Solution

예제 2와 같은 문제를 굳이 내는 이유는 베이즈 정리는 신뢰도를 갱신해 나가는 방법이라고 했는데, 예제 2와 같은 상황이 되면

Hypothesis는 다음과 같이 바꿔 생각할 수 있기 때문이다.

• Hypothesis: 병이 있다고 한 번 진단받았으며 이것이 사실이다.

즉, 예제 1에서 사후확률로 계산된 값이 예제 2에서는 사전확률로 이용되어서, 다시 한번 더 갱신된 사후확률을 계산해주게 된다.

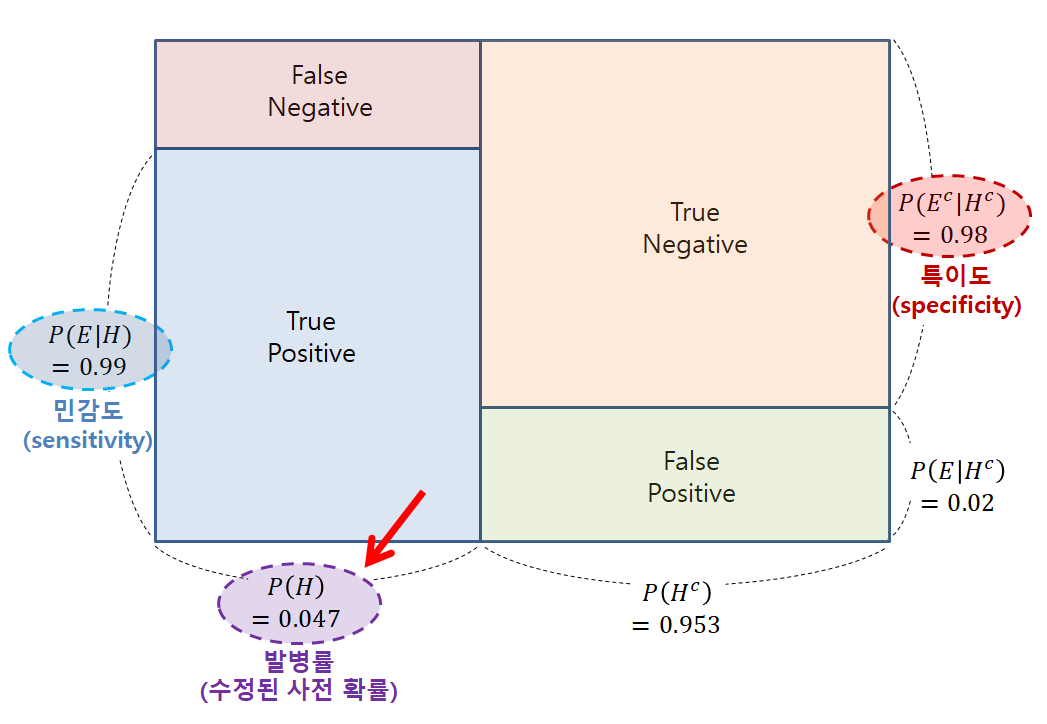
그림 3. 예제 1에서 계산한 사후확률이 예제 2에서 사전확률로 다시 주어지고 (빨간 화살표) 이를 이용해 한번 더 갱신된 사후확률을 계산할 수 있다. 그림은 주어진 확률값들의 값을 사각형의 상대적 넓이로 시각화 한 것.

따라서, 우리가 구하고자 하는 $P(H|E)$를 계산하면 결과값은 다음과 같다.

\[P(H|E) = \frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|H^c)P(H^c)} = \frac{0.047\times 0.99}{0.047\times 0.99 + 0.02\times 0.953}\notag\] \[= 0.709\text{ (소숫점 세자리까지 반올림)}\]

즉, 예제 1에서 계산하여 얻은 사전 확률에 근거를 기반으로하여 한번 더 확률(즉, 병이 걸렸다는 사실에 대한 신뢰도)을 갱신해주면

약 70%의 신뢰도로 이 사람은 병에 걸렸을 수 있다고 말할 수 있을 것이다.